电流分压器规则 (CDR) - 交流和直流电路的求解示例

当多条元素并联时，电流分成多条平行路径。并且对于所有等于源电压的元件，电压都是相同的。

也就是说，当电流通过多条并联路径时（使用分压器规则“VDR”或分压器来计算串联电路中的电压），每条路径中的电流分流。通过特定分支的电流值取决于该分支的阻抗。

分流规则或分流规则是广泛用于求解电路的最重要的公式。如果知道各支路的阻抗和总电流，就可以求出通过各支路的电流。

电流总是流过最小阻抗。因此，电流与阻抗成反比关系。根据欧姆定律，进入节点的电流将在它们之间分流，与阻抗成反比。

表示阻抗值越小，电流越大，因为电流选择了电阻最小的路径。阻值越大，电流越小。

根据电路元件，分流器规则可以描述电阻、电感、电容。

电阻电路的电流分压器规则

为了理解电阻分流器规则，让我们看一个电阻并联的电路。电路图如下图所示。

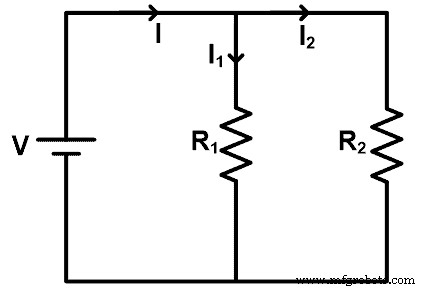
在本例中，为所有电阻器提供直流电源。电阻的电压与源电压相同。但由于并联，电流分成不同的路径。电流在每个节点处分流，电流值取决于电阻。

我们可以借助分流规则直接求出流过各个电阻的电流值。

本例中，源极提供的主电流为I，分为两个电阻R1和R2。通过电阻R1的电流为I1，通过电阻R2的电流为I2。

因为电阻是并联的。因此，等效电阻为 Req。

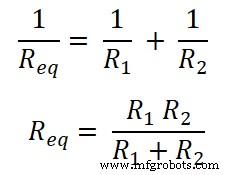
现在，根据欧姆定律；

V =I Req

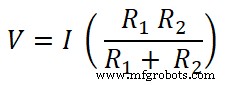
两个电阻均与直流电源并联。因此，电阻两端的电压与源电压相同。而通过电阻R1的电流为I1。

所以，对于电阻R1；

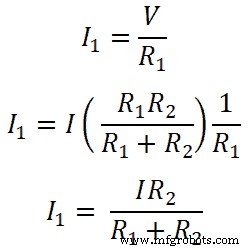
同理，对于电阻R2；

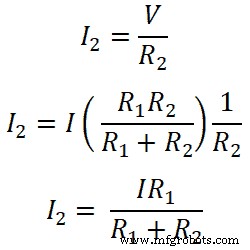
因此，这些等式显示了电阻并联的分流器规则。由这些方程可知，流过电阻的电流等于总电流乘以对侧电阻与总电阻之比。

相关文章：

• 戴维南定理。带有已解决示例的分步指南
• 诺顿定理。带有已解决示例的分步指南

感应电路的分流器规则

当电感并联时，我们可以应用分流器法则求出通过每个电感的电流。为了理解分流器的规则，我们取一个电感并联的电路，如下图所示。

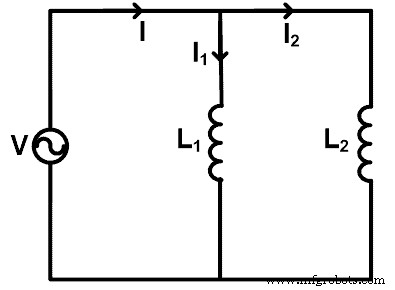
这里，两个电感（L1 和 L2）与源电压 V 并联。通过源的总电流为 I 安培。通过电感L1的电流为I1，通过电感L2的电流为I2。

现在，我们需要找到电流 I1 和 I2 的方程。为此，我们将找到等效电感Leq；

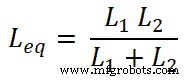
我们知道通过电路的总电流是I，它等于；

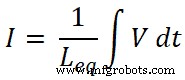
所以，

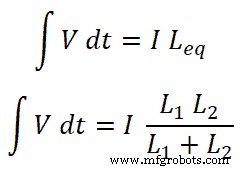
现在，对于电感L1，通过这个电感的电流是I1；

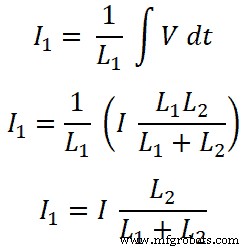
电感L2用；

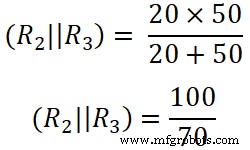
电感的分流规则与电阻的分流规则相同。

电容电路的电流分压器规则

当电容并联时，我们可以利用分流规则求出流过每个电容的电流。为了理解电容的分流规则，我们以电容并联为例，如下图所示。

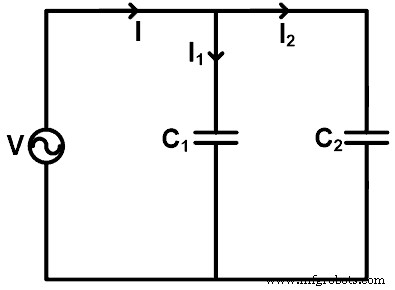
这里，两个电容（C1和C2）并联一个电压源V，流过电容C1的电流为I1，流过电容C2的电流是 I2。通过源提供的总电流为 I。

现在，我们需要找到电流 I1 和 I2 的方程。为此，我们将找到等效电容Ceq；

Ceq =C 1 + C 2

我们知道流过电容器的电流方程。源提供的总电流方程为;

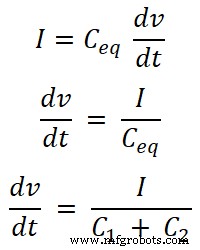
对于电容C1，通过这个电容的电流为I1；

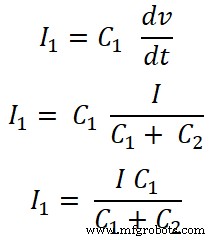
对于电容C2；

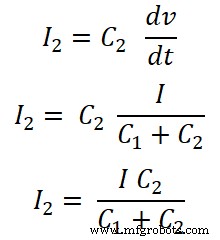
电容的分流规则与电感和电阻的分流规则略有不同。

在电容分流规则中，流过电容的电流是总电流乘以该电容与总电容的比值。

使用 CDR 解决 AC 和 DC 电路示例

直流电路的电流驱动器规则

示例：1

通过给定网络的分流器规则找出通过每个电阻的电流。

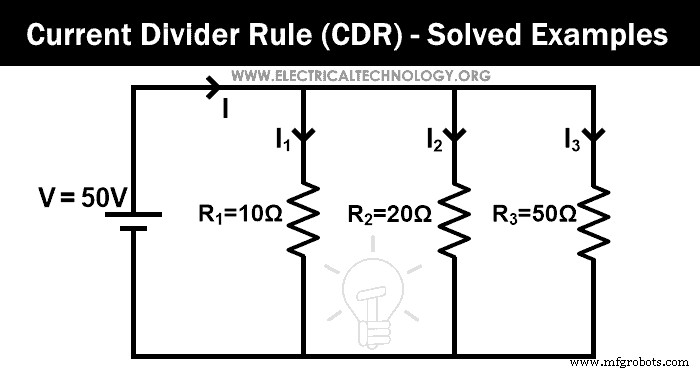
本例中，三个电阻并联。首先，我们找到等效电阻。

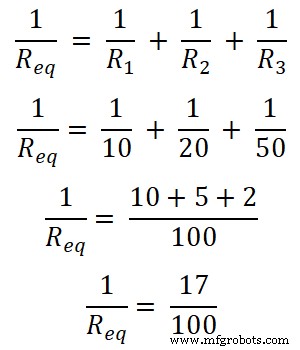
请求 = 100/17

请求 = 5.882Ω

源极提供的总电流为I。所以，根据欧姆定律；

V =I Req

50V =I (5.882Ω)

我 = 50V / 5.882Ω

我 = 8.5 一个

现在，我们对第一个电阻（10Ω）应用分流规则，通过这个电阻的电流为I1；

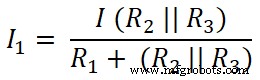
这里R2和R3是并联的。所以，我们需要找到R2和R3之间的等效电阻。

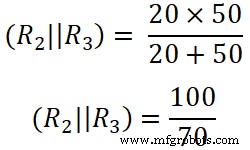
(R 2 || R 3) =14.285Ω

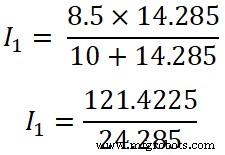
我 1 =4.9999 ≈ 5 A

同理，我们对第二个电阻（20Ω）应用分流规则，通过这个电阻的电流为I2；

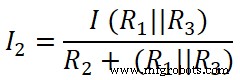
这里，

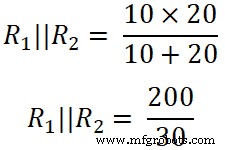
(R 1 || R 3) =8.33 Ω

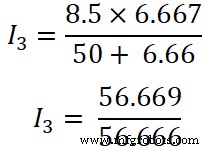
我 2 =2.499 ≈ 2.5 A

现在，我们对第三个电阻（50Ω）应用分流规则，通过这个电阻的电流为I3。

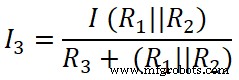
这里，

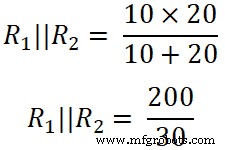
(R 1 || R 2) =6.66Ω

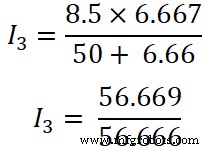
我 3 =1.00 A

所以，所有三个电流的总和将是；

我 1 + 我 2 + 我 3 =5 + 2.5 + 1 =8.5 A

而且这个电流和源提供的总电流是一样的。

交流电路的电流潜水规则

示例 2

假设有一个电阻和电容并联的交流电路，如下图所示。使用分流器规则找到通过电阻器和电容器的电流。考虑 60 Hz 频率。

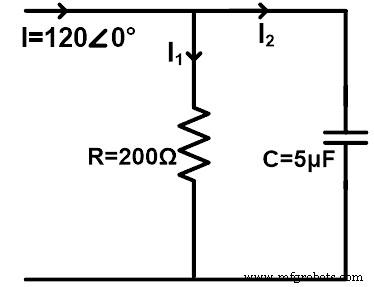
ZR =200 Ω =200∠0°Ω

ZC =1/(2 πf C) =1/(2 π 60(5×10 ⁶ ))

ZC =10 ⁶ / (600π)

ZC =530.78 ∠-90° Ω

现在，根据分流器规则，通过电阻的电流方程为；

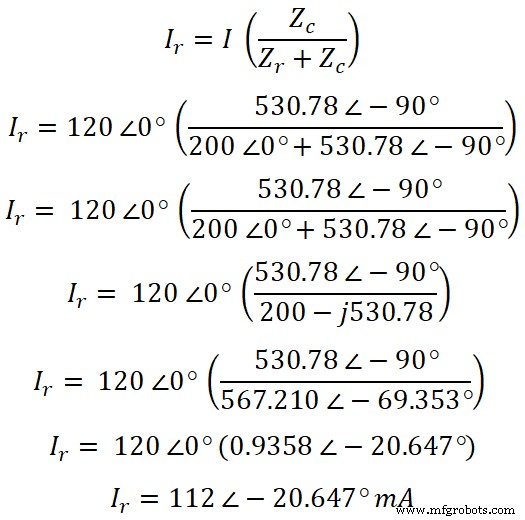
现在，类似地，我们可以发现电流通过了电容器。根据分流规则，流过电容的电流方程为；

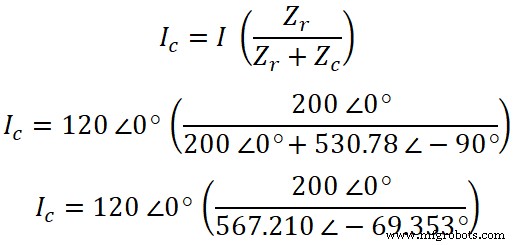
IC =120 ∠0° (0.3526 ∠ 69.353°)

IC =42.31 ∠ 69.353°

如果你想证明这个答案，你可以添加两个电流。并且这个电流的值与源电流相同。

相关电路分析教程：

• 补偿定理 - 证明、解释和求解示例
• 替换定理 - 带求解示例的分步指南
• SUPERNODE 电路分析 - 逐步解决示例
• SUPERMESH 电路分析 - 逐步解决示例
• 基尔霍夫电流和电压定律 (KCL &KVL) |解决的例子
• 克莱默规则计算器 - 电路的 2 和 3 方程系统
• 惠斯通电桥——电路、工作、推导和应用
• 电气和电子工程计算器
• 5000 多个电气和电子工程公式和方程式