数字和符号

数字量的表达是我们往往认为理所当然的事情。这对电子学的研究来说是好事也是坏事。

这很好，因为我们习惯于在分析电子电路的许多计算中使用和操纵数字。

另一方面，我们从小学到的特殊符号系统是not 现代电子计算设备内部使用的系统，学习任何不同的符号系统都需要重新检查根深蒂固的假设。

数字

首先，我们必须区分数字和我们用来表示数字的符号之间的区别。一个号码 是一个数学量，通常在电子学中与电压、电流或电阻等物理量相关。有许多不同类型的数字。这里只是几种类型，例如：

整数：
1, 2, 3, 4, 5, 6, 7, 8, 9 . . .

整数：
-4, -3, -2, -1, 0, 1, 2, 3, 4 。 . .

无理数：
π（约 3.1415927）、
e（约 2.718281828）、
任意素数的平方根

真实数字：
（所有一维数值，负数和正数，
包括零、整数、整数和无理数）

复杂数字：
3 - j4 , 34.5 ∠ 20 ^o

不同类型的数字在物理世界中有不同的应用。整数非常适合计算离散对象，例如电路中的电阻器数量。当需要整数的负等价时，需要整数。

无理数是不能精确表示为两个整数之比的数字，完美圆的周长与其直径 (π) 的比值就是一个很好的物理例子。我们在直流电路中习惯处理的电压、电流和电阻的非整数量可以表示为实数，可以是小数形式，也可以是小数形式。

然而，对于交流电路分析，实数无法捕捉幅度和相位角的双重本质，因此我们转向使用矩形或极坐标形式的复数。

符号

如果我们要使用数字来理解物理世界中的过程、进行科学预测或平衡我们的支票簿，我们必须有一种象征性地表示它们的方法。

换句话说，我们可能知道我们的支票账户里有多少钱，但为了记录它，我们需要制定一些系统来在纸上符号化这个数量，或者以某种其他形式的记录保存和追踪。

模拟和数字

我们有两种基本方法可以做到这一点：模拟和数字。使用模拟表示，数量以无限可分的方式进行符号化。通过数字表示，将数量以离散包装的方式进行符号化。

模拟表示

您可能已经熟悉货币的模拟表示，但没有意识到它是什么。你见过用温度计的图片制作的筹款海报，上面红色柱子的高度表示为这项事业筹集的金额吗？筹到的钱越多，海报上的红色墨水栏就越高。

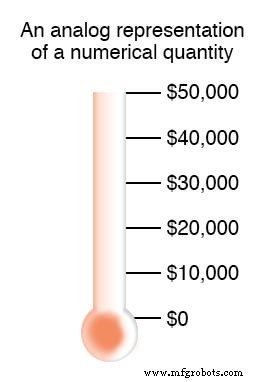
这是一个数字的模拟表示的示例。对该列的高度进行细分以表示帐户中的金额没有实际限制。更改该列的高度是可以在不改变其本质的情况下完成的。

长度是一个物理量，可以任意分割，没有实际限制。计算尺是一种机械装置，它使用完全相同的物理量——长度——来表示数字，并帮助一次对两个或多个数字进行算术运算。它也是一个模拟设备。

数字表示

另一方面，数字 用标准符号（有时称为密码）书写的同一货币数字的表示如下所示：

$35,955.38

与带有红色柱子的“温度计”海报不同，上面的那些象征性字符无法细分：特定的密码组合代表一个数量，仅代表一个数量。

如果向帐户中添加更多资金（+ 40.12 美元），则必须使用不同的符号来表示新余额（35,995.50 美元），或至少以不同模式排列的相同符号。这是数字表示的一个例子。

计算尺（模拟）的对应物也是一个数字设备：算盘，珠子在杆上来回移动以象征数字：

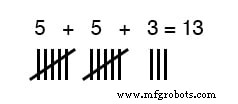
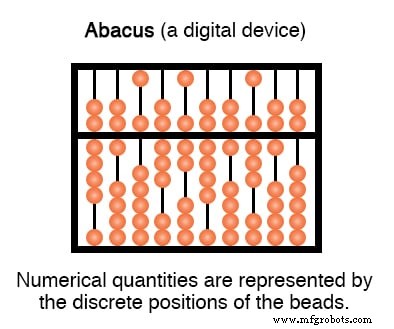
模拟和数字表示的对比

我们来对比一下这两种数值表示方法：

模拟数字
---------------------------------------------- --------------------
直观理解 ----------- 需要训练来解释
无限可分--- -----------离散
容易出现精度误差------绝对精度

数字符号的解释是我们倾向于认为理所当然的事情，因为它已经教给我们很多年了。但是，如果您尝试向不了解十进制数字的人传达某种数量的东西，那么该人仍然可以理解简单的温度计图表！

无限可分与离散和精度的比较实际上是同一枚硬币的反面。数字表示是由单独的、离散的符号（十进制数字和算盘）组成的事实意味着它能够以精确的步骤对数量进行符号化。

另一方面，模拟表示（例如计算尺的长度）不是由单独的步骤组成，而是由连续的运动范围组成。计算尺将数值表征为无限分辨率的能力是对不精确性的权衡。

如果计算尺被碰撞，则会在“输入”到其中的数字表示中引入错误。然而，在珠子完全脱离原位（足以代表不同的数字）之前，必须更用力地撞击算盘。

请不要认为数字表示一定比模拟更准确，从而误解了这种精度差异。仅仅因为时钟是数字的并不意味着它总是比模拟时钟更准确地读取时间，它只是意味着解释 其显示不那么模棱两可。

通过讨论无理数的表示，可以进一步阐明模拟与数字表示的可分性。诸如 π 之类的数被称为无理数，因为它们不能准确地表示为整数的分数或整数。

尽管您过去可能已经了解到分数 22/7 可用于计算中的 π，但这只是一个近似值。实际数字“pi”不能用任何有限或有限的小数位数精确表示。 π 的数字永远不变：

3.1415926535897932384。 . . . .

至少在理论上，可以设置一个计算尺（甚至是温度计的柱子）来完美地表示数字 π，因为模拟符号对它们可以增加或减少的程度没有最小限制。

如果我的计算尺显示的数字是 3.141593 而不是 3.141592654，我可以稍微多一点（或少一点）让幻灯片更接近它。然而，对于数字表示，例如算盘，我需要额外的杆（占位符或数字）来表示 π 以进一步精确度。

一个有 10 根杆的算盘根本不能代表数字 π 的 10 位以上，无论我如何设置珠子。为了完美地表示 π，算盘必须有无数的珠子和杆子！当然，权衡是调整和读取模拟符号的实际限制。

实际上，计算尺的刻度不能精确到第 10 位，因为刻度上的标记太粗糙，人类的视力太有限。另一方面，算盘可以设置和阅读，完全没有解释错误。

此外，模拟符号需要某种标准来进行比较以进行精确解释。计算尺在幻灯片的长度上印有标记，以将长度转换为标准数量。

甚至温度计图表也沿其高度写有数字，以显示红色柱对于任何给定的高度代表多少钱（以美元为单位）。想象一下，如果我们都试图通过将手分开不同的距离来相互交流简单的数字。

数字 1 可以表示为将我们的手分开 1 英寸，数字 2 表示为 2 英寸，依此类推。如果有人将双手相距 17 英寸来表示数字 17，那么周围的每个人是否都能立即准确地将这个距离解释为 17？可能不会。

有些人会猜短（15 或 16），有些人会猜长（18 或 19）。当然，吹嘘自己的渔获量的渔民不介意高估数量！

也许这就是为什么人们普遍选择数字符号来表示数字，尤其是整数和整数，它们在日常生活中的应用最为广泛。

用我们手上的手指，我们有一个现成的方法来表示从 0 到 10 的整数。我们可以在纸、木头或石头上做哈希标记来表示相同的数量很容易：

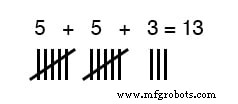
但是，对于大数，“哈希标记”计算系统效率太低。