MATLAB - 微分
MATLAB 提供了 diff 用于计算符号导数的命令。在最简单的形式中,您将要区分的函数作为参数传递给 diff 命令。
例如,让我们计算函数 f(t) =3t 2 的导数 + 2t -2
示例
创建一个脚本文件并在其中输入以下代码 -
syms t f = 3*t^2 + 2*t^(-2); diff(f)
当上面的代码编译并执行时,它会产生以下结果 -
ans = 6*t - 4/t^3
以下是上述计算的八度等价 -
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)
Octave 执行代码并返回以下结果 -
ans = -(4.0)*t^(-3.0)+(6.0)*t
微分基本规则的验证
让我们简要说明用于微分函数的各种方程或规则并验证这些规则。为此,我们将一阶导数写为 f'(x),二阶导数写为 f"(x)。
以下是区分规则 -
规则 1
对于任何函数 f 和 g 以及任何实数 a 和 b 都是函数的导数 -
h(x) =af(x) + bg(x) 关于 x 由 -
给出h'(x) =af'(x) + bg'(x)
规则 2
总和 和减法 规则规定,如果 f 和 g 是两个函数,f' 和 g' 分别是它们的导数,那么,
(f + g)' =f' + g'
(f - g)' =f' - g'
规则 3
产品 规则规定,如果 f 和 g 是两个函数,f' 和 g' 分别是它们的导数,那么,
(f.g)' =f'.g + g'.f
规则 4
商 规则规定,如果 f 和 g 是两个函数,f' 和 g' 分别是它们的导数,那么,
(f/g)' =(f'.g - g'.f)/g 2
规则 5
多项式 或基本幂律规定,如果 y =f(x) =x n ,然后 f' =n。 x (n-1)
该规则的直接结果是任何常数的导数为零,即,如果 y =k , 任何常数,然后
f' =0
规则 6
链 规则指出,函数 h(x) =f(g(x)) 的函数的导数 关于x是,
h'(x)=f'(g(x)).g'(x)
示例
创建一个脚本文件并在其中输入以下代码 -
syms x syms t f = (x + 2)*(x^2 + 3) der1 = diff(f) f = (t^2 + 3)*(sqrt(t) + t^3) der2 = diff(f) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = diff(f) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = diff(f) f = (x^2 + 1)^17 der5 = diff(f) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = diff(f)
运行文件时,MATLAB 显示以下结果 -
f = (x^2 + 3)*(x + 2) der1 = 2*x*(x + 2) + x^2 + 3 f = (t^(1/2) + t^3)*(t^2 + 3) der2 = (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2 f = (x^2 + 1)^17 der5 = 34*x*(x^2 + 1)^16 f = 1/(t^3 + 3*t^2 + 5*t - 9)^6 der6 = -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7
以下是上述计算的八度等价 -
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)
Octave 执行代码并返回以下结果 -
f = (2.0+x)*(3.0+x^(2.0)) der1 = 3.0+x^(2.0)+(2.0)*(2.0+x)*x f = (t^(3.0)+sqrt(t))*(3.0+t^(2.0)) der2 = (2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0)) f = (1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0)) der3 = (-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x) f = (1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x) der4 = (1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x) f = (1.0+x^(2.0))^(17.0) der5 = (34.0)*(1.0+x^(2.0))^(16.0)*x f = (-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0) der6 = -(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)
指数、对数和三角函数的导数
下表提供了常用指数、对数和三角函数的导数 -
| 函数 | 导数 |
|---|---|
| c a.x | c a.x .ln c.a(ln为自然对数) |
| e x | e x |
| ln x | 1/x |
| lncx | 1/x.ln c |
| x x | x x .(1 + ln x) |
| 罪(x) | cos(x) |
| cos(x) | -sin(x) |
| tan(x) | 秒 2 (x),或 1/cos 2 (x),或 1 + tan 2 (x) |
| 婴儿床(x) | -csc 2 (x),或 -1/sin 2 (x) 或 -(1 + 婴儿床 2 (x)) |
| 秒(x) | sec(x).tan(x) |
| csc(x) | -csc(x).cot(x) |
示例
创建一个脚本文件并在其中输入以下代码 -
syms x y = exp(x) diff(y) y = x^9 diff(y) y = sin(x) diff(y) y = tan(x) diff(y) y = cos(x) diff(y) y = log(x) diff(y) y = log10(x) diff(y) y = sin(x)^2 diff(y) y = cos(3*x^2 + 2*x + 1) diff(y) y = exp(x)/sin(x) diff(y)
运行文件时,MATLAB 显示以下结果 -
y = exp(x) ans = exp(x) y = x^9 ans = 9*x^8 y = sin(x) ans = cos(x) y = tan(x) ans = tan(x)^2 + 1 y = cos(x) ans = -sin(x) y = log(x) ans = 1/x y = log(x)/log(10) ans = 1/(x*log(10)) y = sin(x)^2 ans = 2*cos(x)*sin(x) y = cos(3*x^2 + 2*x + 1) ans = -sin(3*x^2 + 2*x + 1)*(6*x + 2) y = exp(x)/sin(x) ans = exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2
以下是上述计算的八度等价 -
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)
Octave 执行代码并返回以下结果 -
y = exp(x) ans = exp(x) y = x^(9.0) ans = (9.0)*x^(8.0) y = sin(x) ans = cos(x) y = tan(x) ans = 1+tan(x)^2 y = cos(x) ans = -sin(x) y = log(x) ans = x^(-1) y = sin(x)^(2.0) ans = (2.0)*sin(x)*cos(x) y = cos(1.0+(2.0)*x+(3.0)*x^(2.0)) ans = -(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0)) y = sin(x)^(-1)*exp(x) ans = sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)
计算高阶导数
为了计算函数 f 的高阶导数,我们使用语法 diff(f,n) .
让我们计算函数 y =f(x) =x .e -3x 的二阶导数
f = x*exp(-3*x); diff(f, 2)
MATLAB 执行代码并返回以下结果 -
ans = 9*x*exp(-3*x) - 6*exp(-3*x)
以下是上述计算的八度等价 -
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)
Octave 执行代码并返回以下结果 -
ans = (9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)
示例
在这个例子中,让我们解决一个问题。假设函数 y =f(x) =3 sin(x) + 7 cos(5x) .我们必须找出方程 f" + f =-5cos(2x) 成立。
创建一个脚本文件并在其中输入以下代码 -
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
当您运行该文件时,它会显示以下结果 -
No, the equation does not hold true Value of LHS is: -168*cos(5*x)
以下是上述计算的八度等价 -
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Octave 执行代码并返回以下结果 -
No, the equation does not hold true Value of LHS is: -(168.0)*cos((5.0)*x)
找出曲线的最大值和最小值
如果我们正在寻找一个图的局部最大值和最小值,我们基本上是在寻找函数图上特定位置的最高点或最低点,或符号变量的特定值范围。
对于函数 y =f(x),图上斜率为零的点称为平稳点 .换句话说,静止点是 f'(x) =0。
为了找到我们微分的函数的驻点,我们需要将导数设为零并求解方程。
示例
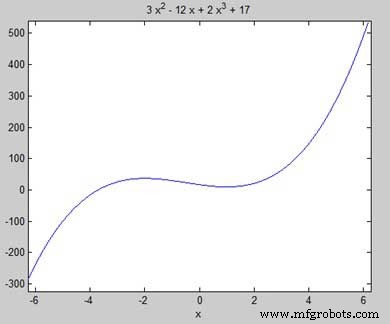
让我们找到函数 f(x) =2x 3 的驻点 + 3x 2 − 12x + 17
采取以下步骤 -
首先让我们输入函数并绘制它的图形。
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y)
MATLAB 执行代码并返回以下图 -
这是上述示例的 Octave 等效代码 -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.eps
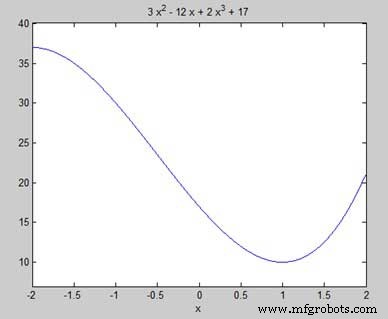
我们的目标是在图上找到一些局部最大值和最小值,所以让我们在图上找到区间 [-2, 2] 的局部最大值和最小值。
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y, [-2, 2])
MATLAB 执行代码并返回以下图 -
这是上述示例的 Octave 等效代码 -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.eps
接下来,让我们计算导数。
g = diff(y)
MATLAB 执行代码并返回以下结果 -
g = 6*x^2 + 6*x - 12
这是上述计算的 Octave 等价物 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
Octave 执行代码并返回以下结果 -
g = -12.0+(6.0)*x+(6.0)*x^(2.0)
让我们求解导数函数 g,以获得它变为零的值。
s = solve(g)
MATLAB 执行代码并返回以下结果 -
s = 1 -2
以下是上述计算的八度等价 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
Octave 执行代码并返回以下结果 -
g = -12.0+(6.0)*x^(2.0)+(6.0)*x ans = -2 1
这与我们的情节一致。所以让我们在关键点 x =1, -2 处评估函数 f。 我们可以使用 subs 替换符号函数中的值 命令。
subs(y, 1), subs(y, -2)
MATLAB 执行代码并返回以下结果 -
ans = 10 ans = 37
以下是上述计算的八度等价 -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)
ans = 10.0 ans = 37.0-4.6734207789940138748E-18*I
因此,函数 f(x) =2x 3 上的最小值和最大值 + 3x 2 − 12x + 17,在区间 [-2,2] 中为 10 和 37。
求解微分方程
MATLAB 提供了 dsolve 符号求解微分方程的命令。
dsolve 的最基本形式 求解单个方程的命令是
dsolve('eqn')
eqn 是用于输入方程式的文本字符串。
它返回一个符号解,其中包含一组任意常数,MATLAB 标记为 C1、C2 等。
您还可以指定问题的初始条件和边界条件,以逗号分隔的列表形式跟随等式 -
dsolve('eqn','cond1', 'cond2',…)
为了使用 dsolve 命令,衍生物用 D 表示 .例如,像 f'(t) =-2*f + cost(t) 这样的等式输入为 -
'Df =-2*f + cos(t)'
高阶导数用导数后的D表示。
例如方程 f"(x) + 2f'(x) =5sin3x 应输入为 -
'D2y + 2Dy =5*sin(3*x)'
让我们举一个一阶微分方程的简单例子:y' =5y。
s = dsolve('Dy = 5*y')
MATLAB 执行代码并返回以下结果 -
s = C2*exp(5*t)
让我们再举一个二阶微分方程的例子:y" - y =0, y(0) =-1, y'(0) =2。
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')
MATLAB 执行代码并返回以下结果 -
ans = exp(t)/2 - (3*exp(-t))/2
MATLAB


