在蓝宝石上生长的外延 n 型掺杂 GaN 层的红外反射分析

背景

近年来，人们对 III 族氮化物材料，尤其是 GaN 材料产生了浓厚的兴趣 [1, 2]。由于生长技术的突破，外延GaN薄膜在蓝光和紫外发光二极管（LED）[3]、激光器[4]和微电子器件等光电子器件中得到了广泛的应用。例如，高功率和高频场效应晶体管 [5, 6]。自由载流子的浓度和迁移率是决定器件在应用中性能的关键参数。多层 GaN 基器件结构中自由载流子浓度和迁移率的霍尔测量不是一项简单且耗时的技术任务，需要将欧姆接触连接到每个测量层和专门的测量程序。

傅里叶变换红外 (IR) 反射光谱和拉曼光谱是非接触式和非破坏性方法，不仅可以研究声子振动，还可以表征载流子特性 [7]。然而，共焦微拉曼光谱的已知问题是由于光的折射而导致深度空间分辨率下降 [8]。它显示在参考文献中。 [6] 在激发波长为 488.0 nm 的多层 GaN 结构深度扫描时，深度分辨率仅为 1.8 μm 左右，而横向分辨率约为 210 nm。由于干涉效应和折射率色散在宽光谱范围内的影响，红外光谱克服了这一问题。

早在 1973 年，A.S. Baker [9]，但这种薄膜的空间不均匀性和整体低结构质量显着限制了所得结果的实际应用。然而，证明了确定 GaN 薄膜中光学声子和自由载流子吸收参数的可能性。纵向光学声子的详细研究- 体 GaN 中的等离子体耦合 (LOPC) 模式由 Perlin 等人执行。 [10] 使用拉曼光谱和舒伯特等人。 [11] 使用红外椭偏仪。还详细研究了不同衬底对立方和纤锌矿 GaN 薄膜光学性能的影响 [12, 13]。考虑到缺乏原生 GaN 衬底，结果表明，使用蓝宝石衬底进行 GaN 膜的外延生长是在高温下工作的器件中开发的最佳选择。六方蓝宝石的红外反射光谱研究 [14] 显示出复杂的光谱，其形状在很大程度上取决于偏振和入射角。这使得在蓝宝石衬底上生长的薄 GaN 膜中声子模式的光谱特性和自由载流子特性的测量和确定变得非常复杂。

Thus, proper selection of spectral analysis algorithm and the form of dielectric function are of great importance for the analysis of the IR reflectance spectra of multilayer GaN-on-sapphire structures [15,16,17].本文展示了应用红外反射光谱和 2 × 2 传递矩阵方法分析具有不均匀深度和掺杂分布的平面 GaN 基多层结构的可能性，这些结构实际上可以是不同类型的半导体 III-氮化物-基于垂直设计的器件结构，如发光和整流二极管、耿氏二极管、高电子迁移率晶体管（HEMT）等

方法

实验性

被调查的n ⁺ /n0/n ⁺ -GaN 结构在 Al2O3 (0001) 衬底上的 MOCVD GaN 模板上在 800 °C 的温度下通过等离子体辅助分子束外延生长，使用 N2 流速为 0.5 sccm 和 RF 等离子体功率为 350 W（图 1） ）。这导致 ∼ 0.27 ML s ⁻¹ 的增长率 .首先，在 MOCVD GaN 模板上生长 0.3 μm 厚的 GaN 缓冲层。 0.8 微米厚的 Si 掺杂 GaN 层之后是 1.75 微米厚的未掺杂 GaN 层和 0.4 微米厚的 Si 掺杂 GaN 层（图 1）。 n ⁺ 的标称Si掺杂浓度 -GaN层为 ∼ 10 ¹⁹ 厘米 ⁻³ .

研究的n ⁺ 示意图 /n0/n ⁺ -GaN-模板/(0001)蓝宝石衬底上生长的GaN结构

为了检查不同载流子浓度的区域，使用 K2S2O8-KOH 水溶液（KSO-D 蚀刻系统）通过光蚀刻方法在化学配置中检查所研究结构的切割边缘 [18]。这种方法允许通过使用表面轮廓测量蚀刻速率来揭示不同载流子浓度的区域并可视化相对载流子浓度差异 [19, 20]。对研究样品的横截面进行光蚀刻 3 分钟。之后，通过扫描电子显微镜（SEM）对样品进行检查。

在 CAMECA IMS6F 系统上使用铯 (Cs ⁺ ) 初级光束，电流保持在 400 nA，以便找到杂质浓度的分布。光栅尺寸约为50 × 50 μm ² ，从直径为 30 μm 的中心区域收集二次离子。对于H、C、O和Si，浓度分别来自H-、O-、C-、Si-物种，并以基体信号Ga-为参考。

300-4000 cm ^-1 光谱范围内的红外反射光谱测量 光谱分辨率为1 cm ⁻¹ 使用配备 Globar 源和带有聚乙烯窗口的氘化硫酸三甘氨酸 (DLaTGS) 检测器的 Bruker Vertex 70 V FTIR 光谱仪在室温下进行。入射角为11°。 S - 偏振光谱是使用 KRS-5 偏振器测量的。以金镜反射光谱作为参考。

光学分析模型描述

层/基材系统的反射率使用 2 × 2 传递矩阵方法计算 [17, 21]，其中可以包括任意数量的层，并自动考虑膜内的干涉效应。各向同性分层系统的 2 × 2 传递矩阵方法允许独立计算 s - 和 p - 在由均匀双轴或单轴各向同性板组成的分层系统的情况下，偏振反射和透射光谱的 c 轴与实验室坐标的 z 轴对齐。在这种情况下，2 × 2的分层系统传递矩阵可以表示为以下视图[21]：

等式中使用了出口介质中场幅度顶部指数中的星号。 (1) 考虑 N 右侧的电场分量值 /N + 1个界面。

\( 2\times 2\kern0.24em {T}_{l,\left(l+1\right)}^{s/p} \) 传递矩阵解释了来自 l -th层，该层内多次反射，以及l/(l + 1)的影响 界面。这样的矩阵可以确定为[17]：

其中 \( {r}_{l,l+1}^{s/p} \) 和 \( {t}_{l,l+1}^{s/p} \) 表示部分反射和透射系数对于 l/(l + 1) 界面，\( {\delta}_l^{s/p} \) 是相移，由 l- 传播后强加给光 s 的第 1 层 - 和 p -偏振光。

s 的相移 - 和 p -通过l-后的偏振光 第层可以确定为[17]：

其中 n l 是 l- 的复折射率 第层，d l 是 l- 的厚度 第层，和θ 是入射角。

s 的部分反射和透射系数 - 和 p -极化可以使用菲涅耳方程计算。例如，s 的部分反射和透射系数 -极化有以下形式[21]：

用部分反射系数和透射系数代替N + 1，可以得到多层叠层的复反射比 方程中的界面（方程（4）） (1) 和所有N的相移 层（等式（3））：

红外介电函数模型

折射率取决于复介电函数ε (ω )，可以写成：

第一项对应于晶格模式色散的贡献，第二项对应于自由载流子激发。

晶格模式对红外响应的贡献ε ^纬度 (ω ) 在声子能量 ℏω 可以使用洛伦兹展宽的分解模型来描述 [22]：

其中 M 是 s 的红外活性极性声子模式的数量 - 或 p - 极化到 c- 轴; ωLOk 和 ωTOk 是频率 (cm ⁻¹ ) 的 k- th LO 和 TO 声子； γLOk 和 γTOk 是它们的阻尼常数 (cm ⁻¹ ）。对于 GaN，参数 ωLOk 和 ωTOk 解释了 E 1(LO), A 1(LO) 和 E 1(TO) 和 A 1(TO)振动模式[23]。

自由载流子种类ε的贡献 ^fc (ω ) 到介电函数可以使用经典的德鲁德近似 [15] 来描述：

与

筛选出的等离子体频率ω p (Eq. (8)) 取决于自由载流子浓度 N , 高频介电常数 ε ∞ 和有效质量 m ^* 自由载流子 (ε 0 是真空介电常数和 e 是单位电荷）。等离子体阻尼参数γ p 取决于光载流子迁移率μ （等式（9））[24]。

ωLO 和 LOPC 模式的参数可以从能量损失函数的虚部确定——\( \mathrm{I}\mathrm{m}\left(-\frac{1}{\varepsilon \left(\omega \right )}\right) \) [7]，其中 ε (ω ) 是复介电函数，从方程获得。 (5).

结果与讨论

SEM 图像（图 2）显示了 n ⁺ 的光刻横截面 /n0/n ⁺ -GaN 结构生长在 GaN-buffer/GaN-template/sapphire 衬底上，其中六个不同的层清晰可见，这是五个具有不同载流子浓度和蓝宝石衬底的 GaN 层。应该注意的是，通过 SEM 测量的研究 GaN 结构的整体厚度与技术一致，并且根据图 1 观察到的 GaN 层可以暂时归因于标称的顶部 Si 掺杂 n ⁺ 区域（第 1 层）、未掺杂的 n0 区域（第 2 层）、底部 Si 掺杂的 n ⁺ 区域（第 3 层）、未掺杂的 GaN 缓冲液（第 4 层）和 GaN 模板。

所研究的 n ⁺ 横截面的 SEM 图像 /n0/n ⁺ -GaN结构。垂直线的不规则图案是在切割过程中（即在光刻之前）形成的，是 Al2O3/GaN 异质结构的非抛光切割的特征。粗糙的金字塔层（针孔 ) 在箭头指示的蓝宝石/GaN模板处 通过光刻显示

此外，为了更深入地了解所研究样品的杂质/掺杂水平，进行了 SIMS 测量。获得的 SIMS 分布图（图 3）与 GaN 层的标称厚度和所研究的多层结构的总厚度具有良好的相关性。所有检测元素（H、C、O、Si）均高于检测限（3至5 × 10 ¹⁶ 在/cm ³ ) 的 SIMS 技术。

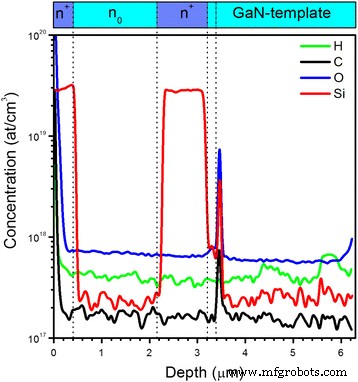
被测n ⁺ 的杂质元素分布 /n0/n ⁺ -通过SIMS从样品表面测量的GaN结构

有意的Si掺杂分布，一般与标称掺杂分布一致，浓度约为2.8 × 10 ¹⁹ 厘米 ⁻³ 在掺杂的顶部和底部 n ⁺ 区域和大约 2.3 × 10 ¹⁷ 厘米 ⁻³ 在未掺杂的 n0 区域。然而，从 SIMS 数据可以看出，也有薄 (<50 nm)-δ 层，Si 浓度为 1.1 × 10 ¹⁹ 厘米 ⁻³ GaN 缓冲器和 GaN 模板之间。需要注意的是，Si掺杂的δ层还含有较高浓度的非故意氧和碳杂质2.4 × 10 ¹⁹ 厘米 ⁻³ 和 1.4 × 10 ¹⁸ 厘米 ⁻³ ，相应地。这个 delta 层与同质外延再生长界面有关，这通常是由于 GaN 模板污染 O、Si 和 C 杂质，在加载技术过程中或再生长开始时从大气中吸收 [25, 26]。

如上所述，SEM 横截面和 SIMS 分析给出了 GaN 层的结构，它与标称参数不同，因为额外的 GaN 区域的激发，但总厚度与标称的一致。为了阐明上面发现的额外 GaN δ 层对所研究结构的 IR 反射光谱的影响，通过构建由六层组成的模型来进行实验光谱的模拟，这些模型对应于标称技术参数、SEM 图像（图 1)，以及根据 SIMS 的七层。基于上述模型的计算光谱如图4所示。

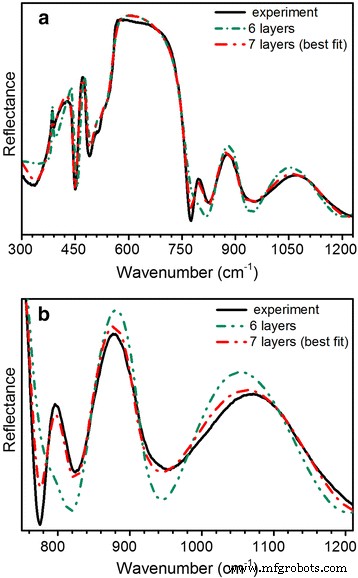
不同层数的红外反射光谱的模拟。所研究的n ⁺ 的实验光谱 /n0/n ⁺ -GaN结构由实线表示 . 一 休息区。 b 750 cm以上范围内的放大光谱 ^-1

从图 4 可以看出，基于 SIMS 剖面的七层模型给出了实验 IR 反射光谱的最佳近似值。因此，与标称技术模型（图 1）相比，使用该模型进行了进一步的模拟和分析，该模型具有修改的参数，并且考虑了技术 GaN 缓冲层和 GaN 模板之间的附加层（图 5）。

7层模型用于模拟研究n ⁺ 的红外反射光谱 /n0/n ⁺ -GaN结构。附加层（绿色 ) 是 GaN 模板和研究的 GaN 层之间的薄界面层

图 6 显示了实验和拟合的理论 ​​s - 研究结构在 11° 入射角的偏振反射光谱。计算出的光谱基于上述模型（图 5）。 GaN 层和蓝宝石衬底的复折射率色散使用方程确定。 (5).蓝宝石衬底被认为是半无限的，这允许忽略衬底内和来自未抛光背面的内部反射。在光谱的reststrahlen区域观察到的复杂结构是由于重叠的GaN和Al2O3reststrahlen带以及干涉效应的组合。将这些数据与计算出的光谱进行比较，不仅可以提供样品各层的厚度信息，而且还有助于根据各种材料的贡献来解释剩余散射区的复杂结构。

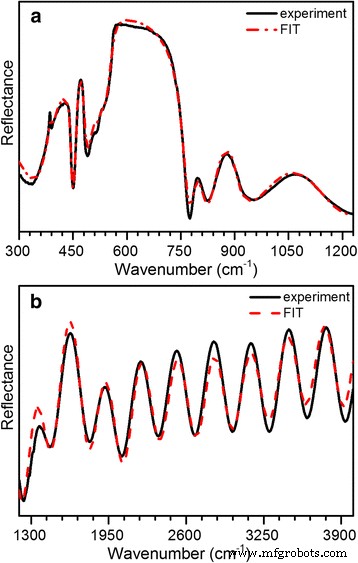
实验性（实线 ) 和最佳拟合计算 (点划线 ) n ⁺ 的红外反射光谱 /n0/n ⁺ -GaN 结构在 GaN 模板/Al2O3 上生长。 一 休息区。 b 干扰区域

根据反射率数据与计算光谱的比较确定层厚度是一个两步过程[27]。首先，在reststrahlen带上方的透明区域中的条纹（ω> 1200 cm ⁻¹ ) 是由于对多层结构的层的干扰效应。通过这种方式，可以估计所研究结构的总厚度，即所有层的总和。

一旦知道堆叠厚度，就可以通过将计算出的光谱与光谱的剩余散射区中的干涉效应进行拟合来确定每层的单独厚度。通过考虑先前确定的总厚度来改变层厚度。在此约束下，反射率高于 1200 cm ⁻¹ 没有显着变化。基于干涉条纹随着层厚度变化而位置偏移的事实，可以将reststrahlen区域的干涉效应与其他特征如TO和LO振动模式区分开来[28]。

在reststrahlen区域的实验光谱逼近过程中，改变了以下模型参数：E的阻尼参数γLO和γTO 1(LO) 和 E 1(TO) 声子模式；等离子体频率ω p;等离子体阻尼参数γ p;和层厚。需要注意的是，只有 E 1 对称声子在 s 中具有 IR 活性 -极化[9]。 E 的初始频率 1(LO) 和 E GaN 和蓝宝石衬底的 1(TO) 声子取自 IR 反射率 [29] 和拉曼散射 [6, 14] 实验。 GaN声子频率的典型值为ωTO =560 cm ⁻¹ 并且ωLO =740 cm ⁻¹ .每一层的声子频率都在拟合过程中进行了细化。得到的带误差条的最佳拟合参数如表1所示。需要说明的是，拟合过程中得到的层厚与SEM数据吻合良好。

参考图 6a，~450 cm ^-1 处的反射峰 可以归因于蓝宝石衬底。在 500–740 cm ^-1 范围内观察到的特征 是由于 GaN 层和蓝宝石reststrahlen 带的重叠特征的组合。为了进行更深入的分析，在reststrahlen带区域模拟了块状GaN和蓝宝石上6.78μm厚的GaN层的IR反射光谱，GaN的厚度对应于研究结构的整体厚度（图7） .从图 7 可以看出，蓝宝石和体 GaN 上 6.78 厚的 GaN 层在 500-740 cm ^-1 范围内的反射光谱 与实验光谱相似。 ~511 cm ⁻¹ 处的小特征 与蓝宝石衬底有关。应该提到的是，在~736 cm ⁻¹ ，有一个弱下降对应于 A GaN 模板的 1(LO) 模式。根据选择规则，A 1(LO) 模式在 s 中被禁止 -偏振红外光谱[9]。记录这种禁止模式的可能原因可能是由于反射附件的孔径以及 GaN 晶体结构的微不均匀性导致的偏振泄漏。具体来说，这可能是由 c 的倾斜引起的 - GaN 柱状纤锌矿结构的轴与薄膜生长平面垂直的方向。在我们的建模中没有考虑这种模式，因为它对结果频谱的影响很小。 750-1200 cm ⁻¹ 范围内的特征 是由于重叠的 GaN:Si 和蓝宝石reststrahlen 带和界面效应。 ~775 cm ⁻¹ 处的下降 与GaN层和蓝宝石的reststrahlen带边缘的界面效应有关。 ~825 cm ⁻¹ 处的大倾角 与等离子体-LO-声子耦合模式（LPP ⁺ ) 的 n ⁺ 层。

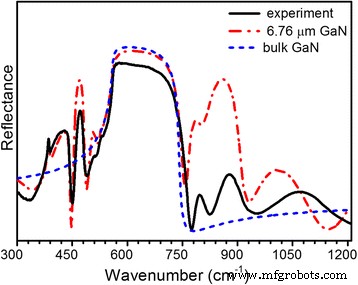
实验性（实线 ) 所研究的 n ⁺ 的红外反射光谱 /n0/n ⁺ - 蓝宝石上 6.78 微米厚 GaN 层的 GaN 结构和计算反射光谱（点划线 ) 和体 GaN（虚线 )

图 8 显示了根据表 1 中给出的振荡器参数计算的每层能量损失函数的虚部，用于估计 E 1-LOPC 模式。可以看出，LOPC 模式的高频分支（LPP ⁺ ) 载流子浓度低于 10 ¹⁷ 厘米 ⁻³ （n0 层和模板）几乎与 E 重合 1(LO) 声子模式。载流子浓度在2 × 10 ¹⁷ 范围内增加 –3 × 10 ¹⁸ 厘米 ⁻³ （图 5）导致 LPP ⁺ 的显着高频偏移和展宽 分支，这表明 LO 声子和等离子体之间的相互作用增加以及电荷载流子迁移率的降低。 LPP ⁺ 的这种行为 分支与 Z.F. 在蓝宝石上生长的 Si 掺杂 GaN 薄膜的 IR 反射率实验数据非常吻合李等人。 [30]，以及体 GaN [10] 和外延层中的拉曼测量 [31]。需要注意的是，低频 LPP ⁻ 在我们的例子中不能可靠地定义 LOPC 的分支，因为 s -在低于 300 cm ^-1 的低频范围内未测量到偏振红外反射光谱 .

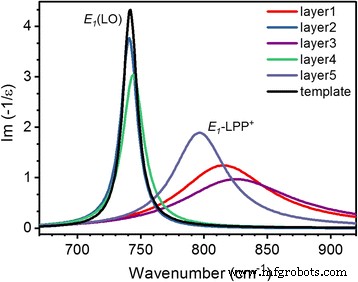
从最佳拟合数据分析获得的每个分析的 GaN 层计算的介电函数的虚部

表 2 中列出的载流子浓度和迁移率的值是使用方程计算的。 (8) 和 (9) 电子有效质量 m* 为 0.2 m0 [32]。可以看出，计算出的载流子浓度分布类似于通过 SIMS 测量获得的 Si 杂质浓度分布（图 3），但与浓度 Si 杂质相比，载流子浓度的数量级较低。 M. Bockowski 等人较早地观察到载流子和掺杂杂质浓度的这种差异。 [33]，并且与受主状态（可能是镓空位）的补偿效应有关，其形成能随着 n 型掺杂的增加而降低 [34]。应该提到的是，n ⁺ 的载流子浓度 按 ~10 ¹⁸ 的顺序排列 厘米 ⁻³ 与我们基于 LOPC 模式分析的类似 GaN 结构的拉曼研究结果非常一致 [6]。获得的载流子迁移率μ随载流子浓度的降低也与GaN霍尔实验[35]和理论模型[36]一致。

发现高频介电常数ε∞ 的值在4.99-5.35 的范围内（表1）。掺杂 n ⁺ 的 ε∞ 增加 与 n0 层相比，层数可能与 α-GaN 带隙的红移有关 [37]。应该注意的是，ε∞ 的值只能以相对较小的误差来确定，仅适用于低导电膜。 ε∞ 的确定精度随载流子浓度而降低，这与当介电模型函数外推到比此处研究的波数更短的波数时，ε∞ 参数占“高频”限制的事实有关 [11]。 300–4000 cm ⁻¹ 的宽光谱范围 分析以减少ε∞ 和其他参数的确定误差，这些参数涉及对n ⁺ 的红外反射光谱建模 层。

结论

详细测量和分析了由在蓝宝石衬底上生长并掺杂不同浓度 Si 杂质的 GaN 层组成的多层结构的红外反射光谱。通过光刻截面的 SEM 对所研究结构的分析表明，其与 GaN 层的工艺参数具有良好的相关性。 SIMS 分析还揭示了在 GaN 缓冲层/GaN-模板界面附近存在具有较高 Si 和 O 杂质含量的薄 delta 层，这与同质外延再生长界面有关。通过将附加层包括在分析中，对所研究的多层结构的红外反射光谱进行建模，从而可以获得实验光谱的最佳拟合。获得的 GaN 层厚度与 SEM 和 SIMS 数据非常吻合。从每个 GaN 层的介电常数 LOPC 模式的光谱依赖性计算显示出 LPP ⁺ 的高频位移和展宽 随着载流子浓度的增加分支。从等离子体频率和阻尼参数计算每个 GaN 层的电荷载流子的浓度和迁移率。获得的载流子浓度分布与 SIMS 获得的相似，但载流子浓度值比 Si 掺杂杂质的浓度小一个数量级，这可归因于缺陷受主态的补偿效应。 Thus, it is demonstrated that IR reflectance spectroscopy and 2 × 2 transfer matrix method can be successfully used for analysis of epitaxial multilayer GaN structures with non-uniform doping profiles, and allow for the determination of the fundamental electron and phonon parameters of each GaN layer.

Change history

缩写

IR:

Infrared

FTIR:

Fourier transform infrared spectroscopy

SEM:

Scanning electron microscopy

SIMS:

Secondary ion mass spectrometry

LOPC:

Longitudinal optical phonon– plasmon coupled