石墨烯介电等离子体波导中模式和色散特性的双重非线性控制

背景

由于石墨烯与金属相比具有独特的电子和光学特性，石墨烯等离子体已经引起了广泛的关注 [1,2,3,4]。在太赫兹和远红外频率范围内，电子的带内跃迁占主导地位，石墨烯表现得像金属。因此，石墨烯可以支持表面等离子体激元（SPP）。对于石墨烯-电介质多层复合结构，研究了 SPP 的模式激发、耦合和传播。在石墨烯平行板波导中发现了准横向电磁模式 [5]。在石墨烯-电介质多层结构中研究了 SPP 的耦合 [6, 7]。对于单层石墨烯片周期性阵列结构，当石墨烯片紧密排列时，SPPs之间会出现强耦合。

大量的努力致力于研究石墨烯-电介质非线性复合结构的光学特性 [8,9,10,11,12]，因为它们在控制微米和纳米尺度的光传播方面具有巨大潜力。对于单层石墨烯情况，讨论了石墨烯和克尔型非线性衬底之间界面处的表面等离子体激元[8]。结果表明，可以通过调整基板的非线性介电常数来调整石墨烯等离子体的波长。对于石墨烯-非线性电介质多层结构，研究了石墨烯等离子体的传播和定位特性，并获得了石墨烯平行板波导的 TM 表面等离子体的准确色散关系 [11]。通过调整非线性介电常数，传播和定位长度受到显着影响。最近，对称和反对称等离子体模式的色散关系已经在石墨烯涂层的克尔板结构中推导出来 [12]。除了典型的前向传播模式外，还发现了对称和反对称模式。

基于石墨烯的强非线性，预测了几种非线性光学效应 [13,14,15,16,17]。内斯特罗夫等人。 [15] 研究了光在石墨烯单层中的非线性传播，发现由于石墨烯的固有非线性，石墨烯单层可以在光频率下支持 TE 和 TM 空间光孤子。最近，Smirnova 等人用多层石墨烯代替单层石墨烯。 [16] 研究了多层石墨烯片的非线性特性，并导出了描述非线性等离子体空间动力学的非线性方程。以往的研究主要集中在单一非线性对石墨烯-电介质结构中光特性控制的影响。在基于石墨烯的光子超晶格 [18, 19] 中引入了双重非线性控制的思想，其中实现了具有深亚波长精度的光子束的电和全光控制。然而，石墨烯-电介质等离子体结构中模式和色散特性的双重非线性控制仍然存在许多问题。因此，本文在石墨烯-电介质-石墨烯波导中同时考虑了石墨烯和电介质的非线性，并研究了双重非线性对模式耦合和色散特性的影响。

方法

石墨烯-非线性介质等离子体波导如图 1 所示，石墨烯平行板的导电率 σ g 被放置在 x =± d /2，其中电介质是介电常数 ε 的克尔型介质 =ε L + α |E | ² .在我们的分析中，石墨烯由于其在一个原子尺度上的厚度而被视为边界。考虑沿 z 传播的横向磁性 (TM) SPP 具有传播常数 β 的方向 并沿 x 指数衰减 分别指向空气和非线性介质。

非线性石墨烯-电介质-石墨烯等离子体波导示意图

对于TM极化，我们知道有三个场分量E x , E z , 和 H 是 .磁场H =H 是 是 和电场E =E x x + E z z 满足方程

其中 ε 0 和 μ 0 是真空的介电常数和磁导率。从方程。 (2) 和 ε =ε L + α |E | ² 我们可以得到

代入方程。 (5) 转化为方程。 (4) 我们有

对于三次方程 [20, 21]

等式的判别式。 (7) 是

设置 \( b=-\left({\varepsilon}_L+\alpha {E}_z^2\right),\kern0.5em c=0 \) 和 \( d=-\alpha {\beta}^2 {H}_y^2/\left({\omega}^2{\varepsilon}_0^2\right) \)，很容易证明方程的判别式。 (6) 满足

Δ <0 表示方程。 (6) 只有一个实解。从卡尔达诺的方法 [20]，我们知道对于三次方程方程。 (7) 它的真正根是

其中 p =c − b ² /3, q =d − 公元前 /3 + 2b ³ /27。使用方程。 (10) 我们可以得到ε .替换ε 在方程式中(2)和(3)通过实解，常微分方程可以用松弛法数值求解。

结果和讨论

来自E的连续性要求 z 和 H 是 , x 处的边界条件 =± d /2 满足 E 1z =E 2z 和 H 2y − H 1y =σ g E z .石墨烯的表面电导率σ g 由 Kubo 公式 [22] 控制，包括带间和带内转换贡献。在太赫兹和远红外频率范围内，带内跃迁贡献占主导地位，表面电导率可以简化为简单的德鲁德类型[23]

其中 e 是电子电荷，μ c 是石墨烯的化学势，ω 是频率，τ 是动量弛豫时间。该模型适用于低温极限（k B T <<μ c ) 在低频 (ℏω ≤ μ c ）。对于强场条件，必须考虑电导率的非线性部分，石墨烯的总电导率读数[16]

其中 E τ 是电场的切向分量，σ ^荷兰 表示非线性电导率 [16]

其中 ν F =0.95 × 10 ⁸ cm/s 是费米速度。

对于石墨烯，只有在太赫兹和远红外频率范围内，其表面电导率才能简化为简单的德鲁德型；因此，我们选择入射波长为λ =10 μm .其他参数固定为ε 1 =1, ε L =2.25, α =5 × 10 ^{− 16} (m/v) ² [24] E F =0.27 ev, τ =1.5 ps。众所周知，石墨烯-电介质-石墨烯线性结构中有两种模式，分别是对称模式和反对称模式。下面，我们将讨论非线性对石墨烯-介电复合结构中模式分布的影响。

设置 H 0 作为入射界面处的初始磁场分量，通过数值求解方程（1、2、3），得到初始磁场强度H的相关性 0 上的传播常数 β 如图 2 所示。归一化传播常数 \( {k}_F=\sqrt{\uppi n} \) 以费米动量 [25] 为单位，其中 n =6 × 10 ¹² cm ^{− 2} 是载流子密度。实线表示只考虑电介质非线性的情况，虚线表示同时考虑电介质和石墨烯非线性的情况。从图 2 我们发现两种情况的模式属性是相同的。存在三个分支，这意味着非线性等离子体波导可以支持三种模式。然而，与单非线性情况相比，双非线性情况的初始场强明显降低。尽管石墨烯非线性等离子体波导可以支持三种模式，但无法区分哪个分支表示对称、反对称或不对称模式。为了确定每个分支的模式特性，我们分别绘制了与图 3 中的 A、B、C 和 D 相关的电场和磁场分布。

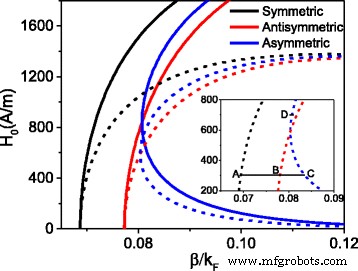
初始磁场强度与传播常数的关系。对于实线 :α =5 × 10 ^{− 16} (米 /v ) ² , σ ^荷兰 =0;对于虚线 :α =5 × 10 ^{− 16} (米 /v ) ² , σ ^荷兰 =2.19 × 10 ^{− 20<​​/sup> i，水平黑色实线 是辅助线}

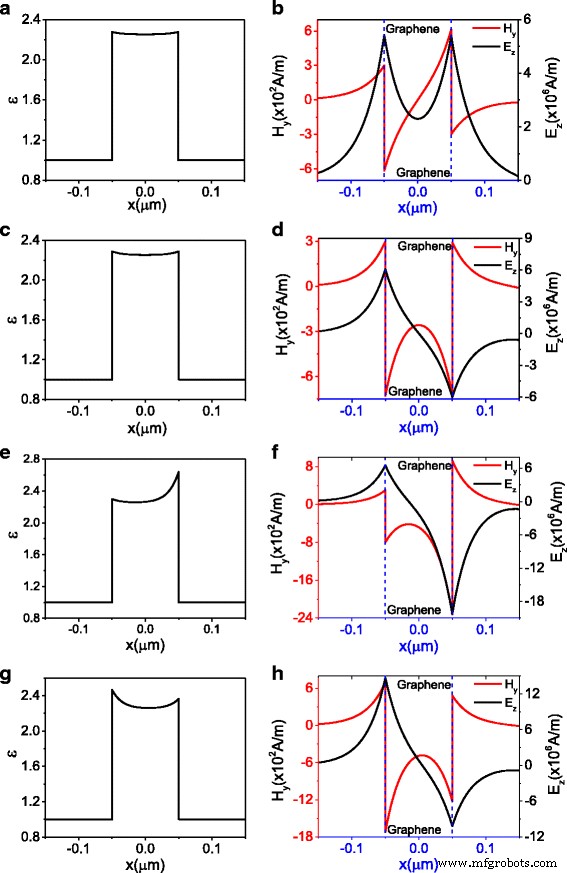
磁性元件H的介电常数和模式分布 是 和电子元件E z . 一 和 b 对应点 A (H 0 =300, β =6.94 × 10 ^{− 2} k F ) 在图 2 中标记为对称模式，c 和 d 对应点 B (H 0 =300, β =7.81 × 10 ^{− 2} k F ) 在图 2 中标记为反对称模式，e 和 f 对应点 C (H 0 =300, β =8.36 × 10 ^{− 2} k F ) 在图 2 中标记为非对称模式，以及 g 和 h 对应点 D (H 0 =700, β =8.07 × 10 ^{− 2} k F )

对于黑色虚线的分支，对应的介电常数和与A相关的场如图3a，b所示，其中介电常数和电场的分布E z 是对称的。因此，该分支代表对称模式。对于红色虚线的分支，与 B 相关的介电常数和场在图 3c、d 中给出。介电常数的分布仍然是对称的；然而，电场分布E z 是反对称的，这意味着该分支是反对称模式。与 C 和 D 相关的介电常数和场的分布绘制在图 3e-h 中。注意到与C和D相关的相应磁场和电场的分布是不对称的；因此，蓝色虚线的分支代表非对称模式。同时，电场的不对称分布导致介电常数的不对称分布。

接下来，我们将注意力转向讨论电介质和石墨烯的非线性对色散关系的影响。图 4 显示了固定初始磁场 (H 0 =300 A/m)和不同的化学势和电介质的非线性系数。在图 4a-c 中，显示了电介质非线性系数对色散关系的影响，其中只考虑了电介质的非线性。当非线性系数和非线性电导率都为零时（α =0, σ ^荷兰 =0)，非线性结构退化为线性结构。在图 4a 中，对于线性情况，仅存在对称和反对称模式。黑色实线和红色实线分别代表对称和反对称模式。当非线性系数不为零时，结构中出现如图 4b、c 所示的支路 III 的非对称模式。随着非线性系数的进一步增大，该系数对色散特性的影响逐渐减弱。

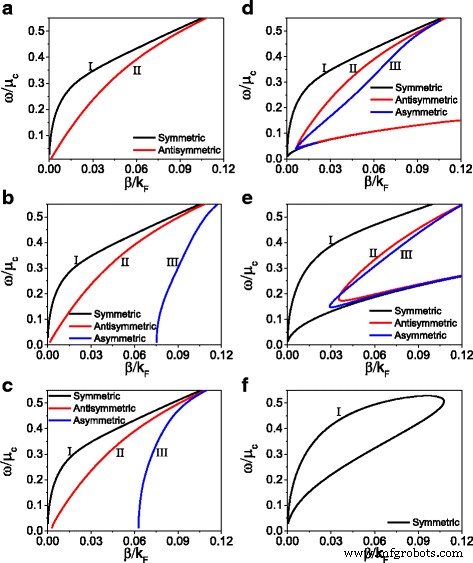
固定初始磁场强度 (H 0 =300 A/m) 并且对于各种非线性系数(a –c ) 和各种化学势 (d –f ）。 一 α =0, μ c =0.27eV, σ 荷兰 =0, b α =5 × 10 ^{− 17} (m/V) ² , μ c =0.27eV, σ 荷兰 =0, c α =5 × 10 ^{− 16} (m/V) ² , μ c =0.27eV, σ 荷兰 =0, d μ c =0.27eV, α =5 × 10 ^{− 16} (m/V) ² , (e ) μ c =0.16eV, α =5 × 10 ^{− 16} (m/V) ² , 和 f μ c =0.10eV, α =5 × 10 ^{− 16} (m/V) ²

下面将同时介绍电介质和石墨烯的非线性，并讨论石墨烯非线性对介质非线性系数固定α的色散关系的影响 =5 × 10 ^{− 16} (m/V) ² .结果如图 4d-f 所示。比较图 4d 和图 4c，可以看出色散关系的折回现象出现在所有三个分支中。从方程。 （13），我们知道石墨烯的非线性可以通过调节化学势来控制。随着石墨烯的非线性从 μ 进一步增加 c =0.27 eV 至 μ c =0.16 eV，如图4e所示，色散关系的折返点向上移动。对于较大的非线性石墨烯（具有较小的化学势μ c =0.10eV)，如图 4f 所示，仅出现对称模式并形成闭环。由图4可知，仅考虑电介质的非线性，色散关系呈现三个分支，随着电介质非线性系数的增加，几乎不变。然而，当我们进一步引入石墨烯的非线性时，就会出现色散关系的折返现象。对于指定的初始磁场 H 0 和化学势的色散关系只显示一个对称的闭环模式。

结论

总之，我们研究了石墨烯介电非线性等离子体波导的模式和色散特性。模式分布、介电常数和色散关系是通过数值求解 TM 极化的麦克斯韦方程获得的。与仅考虑电介质非线性的情况相比，同时考虑电介质和石墨烯的非线性时初始场强明显降低。此外，双非线性显着影响波导的色散特性。特别是，随着石墨烯的非线性增加，反对称和不对称模式合二为一并逐渐消失。因此，在强非线性情况下只能找到对称模式。