石墨烯集成硅微环谐振器的拉曼映射分析

背景

与硅光子学平台的集成是石墨烯在光电检测、光调制和生化传感等应用中可能产生最大影响的地方，这要归功于 CMOS 后端生产线大规模制造的潜力，成本相对较低 [1] ]。事实上，这方面的研究现在已经建立[2, 3]，但为了实现高性能器件，石墨烯转移过程应该优化，石墨烯机械和电子特性的任何加工相关的修改都需要适当的表征和理解。例如，众所周知，石墨烯集成的硅（和其他）基板往往会产生大量与异质材料键合相关的工艺污染物和缺陷，这会影响两种材料之间结处的器件质量。由于这些界面处的应变和无意掺杂而导致的石墨烯能带结构的变化可以通过峰值位置、宽度、不对称性和相对峰值强度的变化显示在拉曼散射特征中。拉曼光谱已被用作评估石墨烯的电子和振动特性 [4] 的敏感工具，包括应变 [5]、掺杂水平 [6]、缺陷密度 [7] 和边缘结构 [8]，尽管这些影响可能是难以与受底物影响的那些分开。石墨烯拉曼峰的强度、宽度、位移率和分裂随应变和p - 和 n 型掺杂已有报道[5, 9,10,11]。

石墨烯表现出三个主要的拉曼散射峰，每个峰都有不同的物理起源：双共振 (DR) D 峰出现在 1350 cm ^-1 [12] 并且通常与无序有关，这意味着它的外观和相对强度通常被用作衡量转移材料质量的指标（即它在高质量、原始材料中很弱或不存在）。另外两个主峰是 G 峰，它来自区域中心声子的石墨面内散射，位于 1580 cm ^-1 [8, 12]，以及出现在 2700 cm ⁻¹ 附近的 2D 峰（D 峰的二阶） [13]。尽管它与 D 峰有关系，但由于它满足基本选择规则 (q =0) 特别是通过电子-声子 DR 散射过程，而 D 峰需要高度局部化的电子缺陷散射以保持动量 [12, 14,15,16]。 G 和 2D 峰的形状、强度和位置允许确定石墨烯层的数量以及任何固有应变和材料中过量载流子的存在[8, 13]。

从许多设备应用的角度来看，石墨烯与硅光子学平台的集成很有趣，例如用于展示增强的生化传感器，其中石墨烯作为吸附物质的高亲和力表面功能层，可以通过下面的硅光子器件中的倏逝光场进行探测。石墨烯的二维性质也导致了光电能带结构，其电荷填充可以通过非常低的功率静电门控进行调整。在这种情况下，“泡利阻塞”效应可以改变材料对入射光子的不透明度，提供极快 (GHz) 光调制或切换的可能性，这可能在电信应用中使用。先前关于石墨烯通过与基于硅光子波导的器件集成的面内线性吸收系数的报告 [17,18,19,20] 产生了截然不同的结果，这表明这些研究中的特定转移过程和衬底界面质量可能在观察到的变化中起一定作用。在这项工作中，使用映射技术展示了石墨烯集成的硅跑道型微环谐振器 (MRR) 上的拉曼 G 和 2D 峰的空间特征。我们的方法是研究 G 和 2D 峰值频率、它们的相对积分强度和宽度，并将这些与空间位置相关联，以阐明底层硅波导对该界面处石墨烯的结构和光电特性的影响。

方法/实验

本研究中的 Si MRR 器件是在商业 Si 代工厂（CEA-LETI，法国）中制造的，包括 335 nm 宽度的条形波导，由具有 2 μm 的商用 220 nm 绝缘体上硅光刻形成- 厚埋氧化层。选择这些波导尺寸，特别是相对较窄的波导宽度（与典型的带状波导相比），以确保在转移后与表面集成石墨烯良好的模式重叠。研究了两种“跑道”型 MRR 设备，其中一种径向分量为 10 微米，另一种为 20 微米，并且都具有相同的 20 微米长的线性截面。在石墨烯转移之前，用丙酮、异丙醇 (IPA)、去离子水和抗蚀剂剥离剂（NMP：1-甲基-2-吡咯烷酮）清洗器件。紧接着在转移之前进行氧等离子体蚀刻（40 秒）。石墨烯通过化学气相沉积 (CVD) 在铜箔 (Gratome-R-Cu, Bluestone Global Tech) 上生长，然后使用聚合物介导的湿转移程序转移到预先清洁的波导上 [21]。石墨烯被图案化，以确保选择性覆盖 MRR 设备，使用光栅扫描光刻和氧等离子体蚀刻。为了确保样品尽可能干净，随后在还原气氛中进行了 270°C 的退火处理，并进行了丙酮清洗，使残留的光刻胶几乎完全去除，如我们的光学图像所示。

拉曼光谱映射是在室温下以背散射配置进行的，使用带有 600 g/mm 光栅的 Horiba LabRAM HR Evolution 光谱仪。散射信号被共聚焦收集并用集成的珀尔帖冷却电荷耦合器件 (CCD) 相机检测。样品由 633 nm 氦氖激光激发，并且在映射过程中样品的机械运动由 Marzhauser 电动显微镜 XYZ 载物台提供。入射激光使用数值孔径为 0.75 的 × 50 物镜聚焦在样品表面。为了避免激光加热，样品上的激光功率密度保持在 2 mW 以下 [22]。获得了两种不同的石墨烯集成硅 MRR 器件的拉曼图，曲率半径为 r =10 μm 和 20 μm。这些图是从 120 × 120 点阵列获得的，每个点之间的步长为 0.25 微米，拉曼 G 和 2D 峰的精确频率、强度和宽度通过将洛伦兹线形拟合到光谱峰来确定.通过使用相同仪器配置（狭缝宽度、光栅和激发源）对单晶硅样品的测量，我们从 4.6 cm ^-1 的主 Si 散射峰的带宽估计了光谱分辨率 或更好。

结果与讨论

为了检查我们是否转移了单层石墨烯，在拉曼映射研究之前，我们还在转移后立即测量了单点拉曼散射信号，图 1（使用 514 纳米雷尼绍 1000 系统）。该光谱揭示了一个弱的拉曼 D 峰，表明结构无序度较低（相当高质量的石墨烯）；强烈（相对于 G 峰）、对称的二维散射模式；和 ~ 1587 cm ⁻¹ 的 G 峰位置 .这种相对强烈的、对称的 2D 散射峰和接近预测值的 G 峰频率的组合，ωG (n ) =1581.6 + 11/(1 + n ^1.6 ) 其中 n 是层数 [23]，证实转移的石墨烯确实是单层 [24]。单层石墨烯集成 MRR (r =10 μm) 显示在图 2a、b 中，石墨烯 G 和 2D 峰的映射区域分别显示在图 2a 和图 2b 中。图 2c、d 是生成的 G 和 2D 峰值位置图，显示频率上移（高达 ~ 11 和 ~ 8 cm ⁻¹ , 分别)，其中石墨烯相对于其悬浮位置位于 MRR 波导结构的顶部。

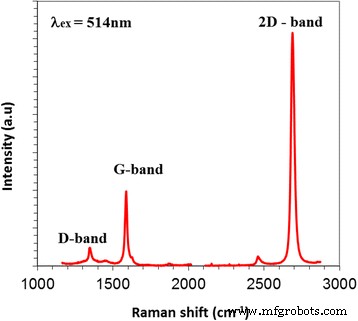
单点拉曼散射光谱（514 nm 激发），我们从中推断出单层石墨烯在此处研究的 Si 波导器件上的转移，这是由于强烈的对称 2D 散射模式和 G 峰值频率，ωG ~ 1587 cm ⁻¹

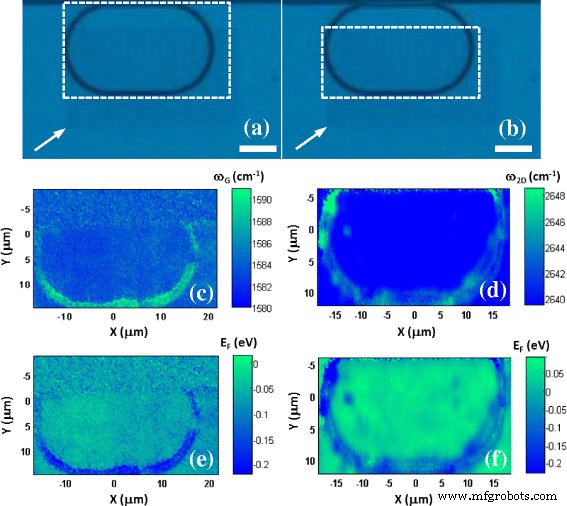
相同石墨烯涂层 Si MRR (r =10-μm 设备）（比例尺 =10 μm）显示了 a 的不同映射区域（白色虚线方块） G 和 b 分别为 2D 峰。石墨烯通过稍暗的对比度显示（其左下角由箭头表示）。 c 和 d 显示相应的峰值位置和 e 和 f 费米能级图，由方程确定。 (1)和(2)分别

移位的 G 和 2D 拉曼峰可能与石墨烯层中的应变或掺杂或这些的组合有关。然而，在低应变极限下（其中 G 峰没有分裂），2D 峰的应变相关位移 (∂ω 2D /∂ε ) 大约是 G 峰 (∂ω G /∂ε ) [5]。我们在这里观察到石墨烯位于波导上的 G 和 2D 峰的大致等效位移表明位移的主要原因不太可能是应变。另一方面，掺杂的 G 和 2D 峰位移的相对速率和方向对载流子类型具有高度特异性 [25]。对于两个电子 (n ) 和孔 (p ) 掺杂，G 峰的频率总是从固有值增加，这意味着 G 峰位置与费米能级的图几乎是关于零对称的。然而，对于 2D 峰值，虽然 p 的适度增加使频率显着上移 -掺杂水平 (~ 15 cm ⁻¹ 对于 3 × 10 ¹³ cm ⁻² )，它从其本征位置几乎保持不变，直到电子浓度为 ~ 3 × 10 ¹³ cm ⁻² ，高于此值时它会迅速降档。这导致费米能级大约为零的 2D 峰位置的高度不对称曲线。我们观察到 G 和 2D 峰在幅度和方向上都相似的变化强烈表明石墨烯是适度的 p 掺杂，与悬浮位置相比，它位于波导上。为了量化这种影响，我们使用以下经验关系（方程（1）和（2））来确定拉曼 G 和 2D 峰位移的近似费米能级位移，在 [25] 之后：

其中 ω 0(G ) (=1580 cm ⁻¹ [26]) 和 ω 0(2D ) (=2640 cm ⁻¹ [9]) 分别是无应变的本征石墨烯（用于 633 nm 激发）的 G 和 2D 峰位置，ω (G ) 和 ω (2D ) 是我们为地图和 E 中的每个点确定的 G 和 2D 峰值位置 F 是以 eV 为单位的费米能级。在图 2e、f 中，我们将这些计算的结果显示为费米能级图，源自图 2c、d 的数据。这些大致等效（如预期的那样），表明悬浮的石墨烯是内在的（E F ~ 0) 但空穴浓度增加（产生 E 的最小值 F 大约 - 0.2 eV），其中石墨烯位于波导结构的顶部。半径为 r 的 MRR 的类似分析 =20 μm（此处未显示）给出了非常相似的结果，表明该效应不依赖于波导几何形状，而是纯粹依赖于材料（衬底）的掺杂效应。这种掺杂的来源几乎可以肯定是在硅/SiO2 和石墨烯之间的界面处局部捕获的静态广告电荷的结果。已知这些 ad 电荷的密度在接受了更积极的清洁处理（例如我们采用的 O2 等离子体蚀刻）的样品中增加[27]。尽管该工艺提供了一个彻底清洁的界面（相对没有污染物），但这种损坏会导致富氧开壳（悬空键型）缺陷，这些缺陷是已知的有效电荷载流子陷阱。

代表性拉曼散射光谱（来自映射）如图 3 所示，揭示了 G 和 2D 峰值频率的上移，其中石墨烯位于底层硅 MRR 波导结构上。

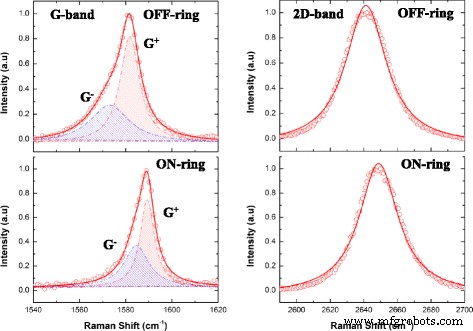
代表性石墨烯 G（左）和 2D（右）平均 (n =3) 拉曼散射峰（633 nm 激发）关闭（顶部）和开启（底部）下方的硅 MRR 波导结构。线代表数据的双（G 峰）或单（2D 峰）洛伦兹拟合。由于面内 E 的简并性降低，G 峰的不对称性 2g 光学声子导致不同的散射模式，标记为 G ⁺ 和 G ⁻ （符合碳纳米管的惯例）

2D 峰被很好地描述 (R ² =0.993) 由单个对称洛伦兹线形，单层石墨烯的特征 [8]。我们注意到，使用 Voigt 函数对 2D 峰的拟合仅略有改善，这表明对仪器展宽的贡献很小。在ON-和OFF-环数据之间的2D散射模式的FWHM中没有观察到可测量的变化（超出标准误差），表明这对载流子浓度不敏感，与之前的观察结果一致[28]。

另一方面，G 峰对于 OFF 和 ON 环条件都相当不对称，因此不能用单个对称函数很好地描述。相反，我们发现它最好被描述 (R ² > 0.995) 由双洛伦兹线形表示，表明两种不同的散射过程。我们注意到主的宽度 (G ⁺ ) 峰值降低 ~ 25% (\( {\Gamma}_{\mathrm{OFF}}^{+} \) ~ 10 cm ⁻¹ , \( {\Gamma}_{\mathrm{ON}}^{+} \) ~ 7.5 cm ⁻¹ ) 从悬浮的石墨烯到它被 MRR 波导结构支撑的地方。这与当前对石墨烯 E“变硬”的理解和先前观察一致 2g 光学声子，由于掺杂 [8]。第二个底层散射模式（G ⁻ )，负责不对称性，宽度也显着减少 ~ 35% (\( {\Gamma}_{\mathrm{OFF}}^{-} \) ~20 cm ⁻¹ , \( {\Gamma}_{\mathrm{ON}}^{-} \) ~ 13 cm ⁻¹ ) 从悬浮的石墨烯到它被 MRR 波导结构支撑的地方。石墨烯拉曼 G 峰的不对称性先前已归因于激光探针区域内的高度局部电荷不均匀性 [28]，即亚微米级，并且在将悬浮石墨烯的拉曼光谱与支持的拉曼光谱进行比较时也已经观察到通过底物 [22]。最近对纳米结构表面支持的石墨烯的研究 [29] 也揭示了 G 带中的多峰精细结构，这被解释为极端曲率或“起皱”的结果，类似于在单壁中观察到的碳纳米管（SWCNT）。在这种情况下，面内的双重退化 E 2g 光模可以在沿纳米管轴 \( {\omega}_G^{+} \) 和垂直于它的声子 \( {\omega}_G^{-} \) 之间分裂，其中分裂程度，\( \Delta {\omega}_G={\omega}_G^{+}-{\omega}_G^{-} \)，是纳米管尺寸的强函数（即曲率)，即使没有任何外部施加的应变 [30]。在单轴应变下的石墨烯 [5] 和静水压力下的孤立 SWCNT 中也观察到 G 峰分裂 [31]，其中曲率敏感的较低频率 (G ^- ) 当纳米管在高压载荷下弯曲和坍塌时，散射模式本身会变宽甚至分裂。我们从这里拟合石墨烯 G 波段光谱注意到，两者的频率差 Δω G 和 G ⁻ 的线宽 模式 (\( {\Gamma}_{\mathrm{OFF}}^{-} \)) 对于挂起的 OFF 环条件比 ON 环情况更大。在没有任何证据（来自峰值位置）全局净应变的情况下，我们推测这可能是悬浮区域中局部平面外起皱的结果，在石墨烯所在的位置“平滑”了由明确定义的底层亚微米 MRR 波导结构支持，这将解释较小的 Δω G 和更窄的 G ⁻ 我们在这里观察到的峰值。

我们还检查了峰值强度的比率，I 二维/我 G，已知与载流子浓度有关，在固有情况下最大，并随着增加而不断减小（n 和 p ) 掺杂水平，主要是因为 2D 模式随着载流子 - 声子散射的增加而猝灭 [22, 32]。然而，虽然我们确实观察到 I 二维/我 G，从石墨烯悬浮的~ 3到波导结构上的~ 2.5，我们注意到，与相同激发激光波长的其他报告[28]相比，这种变化相对于我们观察到的G峰位移程度很小（633 纳米）。值得指出的是，尽管在 [28] 中，I 的数据存在高度分散 二维/我 G 作为 G 峰值位置的函数，似乎随着激发波长的增加而增加，这表明单独这可能不是绝对掺杂水平的最可靠指标，尤其是在低掺杂限制下。

总积分峰强度之比分析，A G /A 2D 考虑了峰宽以及峰高的变化，可用于直接从方程获得载流子浓度。 (3) [22, 32]:

其中 C 是一个常数； e 是电子电荷； γe-ph 是平均电子-声子散射率，之前在 [32] 中确定为 ~ 33 meV； ε (~ 3.9) 是 SiO2 [33] 的介电常数，假设它存在于硅和石墨烯之间的界面（作为天然氧化物层）。这产生 f (e ² /εν f ) ~ 0.069 当 ν f 取为电子速度，1.17 × 10 ⁸ 厘米/秒。我们的测量表明 \( \surd \frac{A_G}{A_{2D}} \) 在石墨烯位于底层硅波导结构顶部的位置比中央悬浮区域更高，再次支持观察到的拉曼光谱偏移的假设是衬底掺杂效应的结果。图 4 显示了我们根据石墨烯 G 和 2D 模式的积分强度之比以及方程确定的费米能级。 (3) 作为沿空间线扫描的位置的函数，该扫描横跨石墨烯集成 MRR 设备的长段中间（对于 10 和 20 微米半径）。峰值费米能级位移与石墨烯位于下面的硅波导结构上的位置一致，为 ~ 0.2 eV，与我们从峰位移确定的以及之前为背栅石墨烯场效应晶体管确定的结果一致 [17] .值得指出的是，尽管我们研究了不同的器件几何形状，与 10-μm 半径结构相比，这导致在 20-μm 半径 MRR 结构上有更大的悬浮石墨烯区域（~ 54-μm 悬浮石墨烯与~ 36 μm），局部空间掺杂模式几乎相同，如图 4 中的高斯拟合所示。

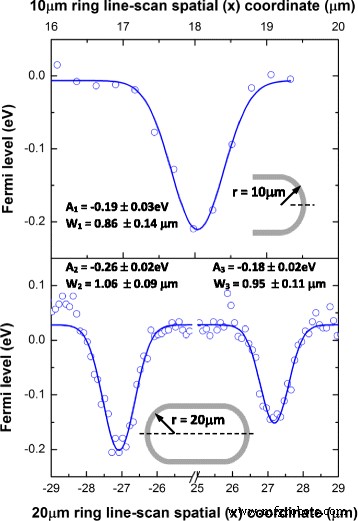
石墨烯费米能级确定（来自 \( \surd \frac{A_G}{A_{2D}} \)）作为沿线扫描（顶部）10-μm 和（底部）20-μm-半径的空间坐标的函数MRR 设备（注意底部 x -轴）。显示拟合（高斯）峰积分面积和宽度以与在设备上获取线扫描数据的位置进行比较

将我们确定的费米能级转换为载流子浓度，n 通过等式(4) [33] 产生 n 的峰值 ~ 3 × 10 ¹² cm ⁻² 关于 MRR 结构，总体上与之前的报告一致[26]：

最后，我们在 Lee 等人介绍的所谓矢量分解图中检查了来自我们测量数据（来自三个线扫描）的 G 和 2D 峰值位置之间的相关性。 [34]，图 5。

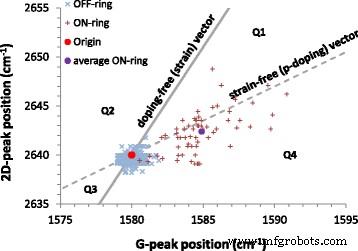
G-2D 相关图显示了石墨烯集成 MRR 中三个线扫描测量的数据。红色十字是石墨烯位于 MRR 结构上的点，紫色点代表这些坐标值的平均值，蓝色十字是石墨烯悬浮在 MRR 上（关闭底层结构）。红点是石墨烯在 633 nm 激光激发下的无应变固有坐标值，它定义了原点。虚线表示无应变 (p -doping) 向量，Δω2D/ΔωG ~ 0.7，实线表示无掺杂（应变）向量，Δω2D/ΔωG ~ 2.2，[34]

在这种类型的图中表示数据使我们能够确定峰值偏移可能受应变影响的程度。这是基于这样一个事实，即应变峰值位置比的变化率 (Δω 2D /Δω G ~ 2.2) 对于那些与掺杂 (∆ω 2D /Δω G ~ 0.7) [34]。因此 G-2D 空间中的任何坐标点都可以分解为应变，特别是 p 型掺杂载体。随着拉伸应变或p的增加 -掺杂，ω G , ω 2D 坐标值将从原点（本征、无应变位置）沿无掺杂（应变）或无应变（p -掺杂）线，分别。 G-2D 坐标空间被这些应变和掺杂向量分为四个象限 Q1-Q4，因此坐标数据与这些线的任何显着偏差，比如进入区域 Q1 (Q4)，都表明峰值偏移是压缩（拉伸）应变 和 p 组合的结果 - 兴奋剂。禁止在 Q2 和 Q3 内散布数据，因为 n- 和 p -掺杂仅表现为 G 峰位置增加。

我们将固有的、无应变的石墨烯峰值频率坐标定义为原点（红点）[9, 26] 并表示无应变 (p -掺杂）向量（虚线）和无掺杂（应变）向量（实线），在 [31] 之后。三个不同线扫描的数据散布在 OFF 环的原点周围和沿着无应变 (p -doping）ON 环的矢量，平均 ON 环坐标值（紫色点）为 (1584.9, 2642.4)。 ON 环数据沿无应变线的散射增加表明从相对峰移检测到的掺杂水平范围更大，这可能是因为探测由底层亚微米产生的高度局部化衬底掺杂效应的不确定性波导宽度，与探针激光光斑尺寸 (> 1 μm) 相比。尽管数据明显分散，但在 Q4 和 Q1 中，我们不考虑任何显着的全局应变效应，因为平均 ON 环坐标与无应变线非常接近。我们认为我们观察到的峰位移仅是由于硅衬底引起的空穴掺杂，平均 ON 环 G-2D 坐标证实这在 (2 到 3) × 10 ¹² cm ⁻² .

结论

总之，单层 CVD 石墨烯与基于硅波导的 MRR 光子器件集成在一起。为映射区域确定了特征石墨烯拉曼 G 和 2D 峰的频移和积分强度，这些表明费米能级“钉扎”，其中石墨烯位于 Si MRR 结构上，这是由于来自底层硅的无意空穴掺杂造成的/SiO2 波导（衬底掺杂效应）。悬浮区域的数据显示与本征石墨烯没有可测量的区别，但对于支撑区域，确定了~ 0.2 eV 的费米能​​级的最大下移，这对应于~ 3×10¹² cm ⁻² .拉曼 G 峰的不对称性根据石墨烯是悬浮还是支撑而变化，表明掺杂引起的“硬化”和 E 的简并性解除的组合 2g光学模式。当石墨烯与硅光子学平台结合时，尤其是在尝试使用此类平台来确定石墨烯的特性以及优化未来与石墨烯集成的硅光子学器件（如光调制器和传感器）时，应考虑到这些影响。

缩写

CCD：

电荷耦合器件

CEA-LETI：

Commissariat à l'energie et aux energies替代品——信息技术实验室

CMOS：

互补金属氧化物半导体

CVD：

化学气相沉积

DR：

双谐振

FWHM：

半高全宽

MRR：

微环谐振器

NMP：

N-甲基-2-吡咯烷酮

Si：

硅

SiO2 :

二氧化硅

SWCNT：

单壁碳纳米管