超表面/石墨烯混合结构的表面阻抗

介绍

近年来，在先前的文献 [1,2,3,4,5,6] 中提出并研究了具有异常电磁特性的新型人工阻抗超表面。同时，已经引入了多种超表面应用，例如全息术 [1]、高分辨率成像 [2]、地毯斗篷 [3] 和吸收器 [4, 5]。超表面可以在实现薄太赫兹和光学器件方面发挥重要作用。然而，由于超表面的色散响应，许多设备只能工作在单一频段，窄谱无法调谐。最近，通过在很宽的频率范围内改变施加的电压，例如太赫兹甚至光学频率，可以动态控制电导率 [7,8,9,10]，这就是为什么石墨烯证明它是调谐的最佳候选者等离子体和超表面结构的特征[11]。因此，人们提出了许多由超表面和石墨烯设计的器件[12,13,14]。

与此同时，一些用于计算超表面或石墨烯片等效阻抗的分析模型已被用于解释物理机制 [8, 15,16,17,18,19,20]。用于激发石墨烯或超表面模型的平面波可以分为两种不同的方法，即分析方法和计算方法。计算方法是在 Floquet 表达式 [21, 22] 上的工作。使用这种方法的优点是它们不受结构几何形状的限制，最重要的优点之一是它可以提供准确的结果。然而，使用这种方法的商业软件会消耗大量的时间和计算资源。另一方面，开发了更精确和准确的分析方法 [23,24,25,26,27]，它易于使用并提供更好的物理现象分析。尽管有上述优点，但实现特定超表面单元的高精度分析模型的挑战也很突出。幸运的是，已经做出了相当大的努力和工作来预测等效表面阻抗并产生了许多出色的结果 [16, 28]。然而，据作者所知，能够预测这种混合组合的表面阻抗的分析模型尚不清楚。

在本文中，利用 3D 人工吸收器来分析和预测超表面/石墨烯混合结构的阻抗，其中考虑了超表面和石墨烯之间的关系。为了快速计算超表面的表面阻抗，首先开发了解析公式。这些简单而精确的分析公式可以完整地阐明阻抗设计的基本要求。然后，计算石墨烯片的阻抗。最后，我们关注超表面尺寸与化学势μ之间的关系 c ，以及复合结构的阻抗。在这里，通过计算其实部和虚部来讨论超表面/石墨烯混合结构的表面阻抗。据我们所知，几乎没有文献全面报道这种机制。

方法

方形贴片和石墨烯片的阻抗

超表面 - 石墨烯吸收剂的常见结构如图 1a 所示。这种结构简单的吸收器可以通过表面微加工轻松制造。在此配置中，薄导电超表面-石墨烯混合层和金属接地平面由作为间隔物的介电基板隔开。到地面的距离是h .对于与波长相比的小尺寸方形贴片（阵列 D 的周期 ≪ λ ) 和补丁被一个窄槽隔开（槽 D 的宽度 − w ≪ D )，本模型是有效的。根据传输线理论，可以构建吸收结构的等效电路模型（如图1b所示），可以模拟超表面-石墨烯。 A 传输线、短路和电网阻抗 Z mg 分别对介电基板部分、接地平面和顶部图案化混合分层的表面阻抗进行建模。根据传输线理论，输入阻抗Z 这个吸收器的in可以建立如下：

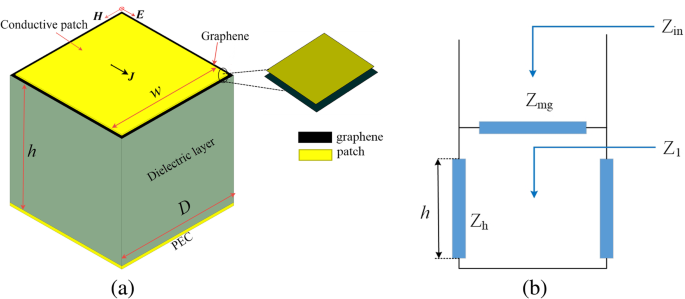
一 超表面-石墨烯吸收体晶胞示意图。 b 局部等效电路模型

其中 Z h 和 k zh 分别是衬底层的阻抗和该区域的传播常数。则法向入射处的吸收率可计算为

很明显，可以从模拟的反射系数中提取超表面-石墨烯片的阻抗。导电贴片尺寸与化学势μ的关系 c 可以找到。

方形贴片的阻抗

当平面波垂直于超表面时，平面贴片阵列充当电容网格（如图 1a 所示）。表面阻抗Z m 可以表示为与平均电流强度相关的方形贴片的电磁特性<J 〉和平均电场强度〈E 〉在补丁平面上：

在有损纯电阻片阻抗 Z 的情况下 s (im Zs=0)，在垂直入射时，贴片的等效阻抗由 Z 表示 m，可以表示为[9, 18]：

其中 \( {\eta}_{\mathrm{eff}=}\sqrt{\mu_0/{\varepsilon}_0{\varepsilon}_{\mathrm{eff}}} \) 代表均匀宿主的波阻抗中，和 D /w 是几何元素。有效相对介电常数可以近似为

此外，网格参数α 理想导电贴片的电致密阵列可以写成

\( {k}_{\mathrm{eff}}={k}_0\sqrt{\varepsilon_{\mathrm{eff}}} \) 是有效宿主介质中的波数。在自由空间中，μ 0, ε 0 和 k 0 分别是磁导率、介电常数和波数。此外，值得指出的是，当波长 λ 远大于 D .

由式(2)可知，等效阻抗不仅由材料薄层电阻率决定，还由阵列周期D决定 和宽度 w 的结构参数。为了验证这些解析公式的确定性，提出了全波模拟获得的结果，并与解析解进行了比较。此处讨论的模拟是通过使用商用软件 Ansoft HFSS 进行的。为了获得超表面-石墨烯吸收体单元的反射特性，实施了周期性边界条件和 Floquet 端口。在其仿真过程中，纯电阻片阻抗与 Z s =35 Ω/sq 沉积在基板上，厚度为 h =20 μm，长度 D =20 μm，ε 的相对介电常数 r =3.2(1 − j 0.045）。为了提取贴片阻抗Z m，根据模拟输入阻抗Z之间的关系 in 和接地介质板的表面阻抗 Z g d，超表面贴片的阻抗可以表示为：

其中 Z gd =jZ d tan(k d h ), \( {Z}_d=\sqrt{\mu_0/{\varepsilon}_0{\varepsilon}_r} \) 是板的特征阻抗， \( {k}_d=\omega \sqrt{\mu_0 {\varepsilon}_0{\varepsilon}_r} \) 是 TEM 模式下与衬底表面正交的传播常数。

通过与基于提取的反射系数的模拟结果进行比较来验证分析结果，如图 2 所示。黑色曲线显示了模拟结果，而红色曲线是使用提出的解析表达式计算的。尽管模拟结果与理论预测之间存在微小差异，但这是由于等式。 (3) 是一个近似方程。总体趋势是一样的。从而证实了我们对该模型的分析表达式的有效性和准确性。

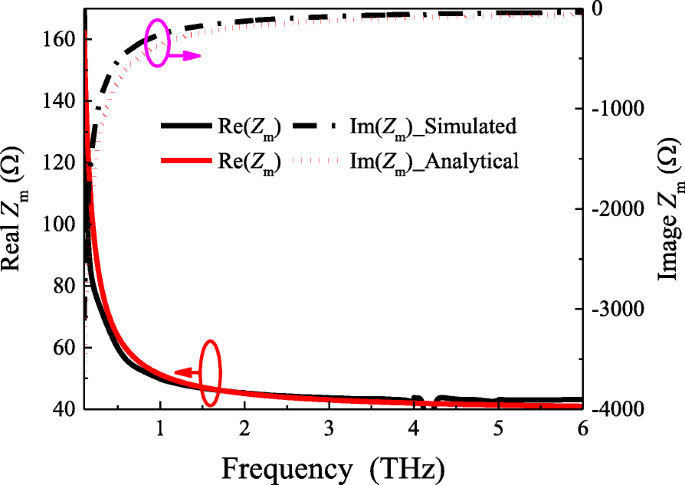
带有w的贴片阵列的模拟和解析网格阻抗 =19 微米

为了研究贴片尺寸对阻抗Z的影响 m 并验证公式（2）的有效性，我们进行了额外的数值模拟。图 3 绘制了电网阻抗 Z 的实部和虚部 m 表示晶胞的各种几何参数。从图 3a 可以看出，阻抗的实部 Z m随着参数w而减小 从 17 μm 增加到 19.5 μm。根据式2，我们可以发现Z的实部 m 与补丁长度成反比 w .然而，虚部显示出相反的趋势，如虚线所示（如图 3b 所示）。考虑到方程。 (2)和(3)，虚部可由

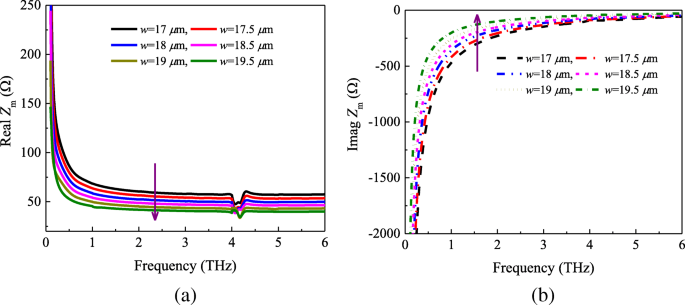
一 真实和b 阻抗的虚部 Z m 不同大小的贴片

由关系式(8)可知，当w 从 17 μm 增加到 19.5 μm，阻抗的虚部 Z m 会增加。

石墨烯片阻抗

石墨烯可以被看作是一个无限薄的表面。当没有外部静磁偏置和空间分散时，表面电导率σ g , 可以通过 [29]

其中 ℏ 是约化的普朗克常数，e 是电子的电荷，k B 是玻尔兹曼常数，而 μ c, ω , τ 和 T 分别是化学势、角频率、弛豫时间和温度。在这里，我们假设 T =300 K 和 τ =0.1 ps 在整个研究中。石墨烯的片阻抗可以计算为

其中 R g 和 X g 为表面电阻和电抗。

石墨烯的片阻抗根据方程计算。 (9) 和 (10)。图 4 显示了表面阻抗与化学 μ 的实部和虚部 C。我们可以发现表面电阻和电抗随着μ的增加而不断减小 C。此外，当化学势固定在一定值时，石墨烯表面电阻的实部在0.2-6 THz范围内几乎保持不变。

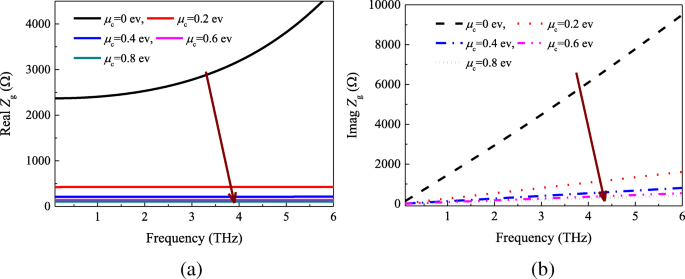
一 真实和b 作为频率和化学势函数的表面阻抗的虚部

结果与讨论

对于石墨烯片上的方形贴片，应确定该混合结构的表面阻抗。在先前的文献[8, 30,31,32,33,34,35,36,37]中，这种混合结构表面的总阻抗Z mg 等于方形贴片阻抗Z的并联组合 m 和石墨烯片阻抗 Z g，即 Z 毫克 =Z 米 ∥ Z g .但是，通过我们的模拟和计算，发现这种关系是不成立的。为了验证真实性，我们模拟了图 1a 所示的超表面 - 石墨烯吸收器单元，然后根据等式（1）检索了薄膜的表面阻抗。图 5 显示了 Z 实部和虚部的解析和模拟值 mg 在不同化学势下与 w =19 微米。

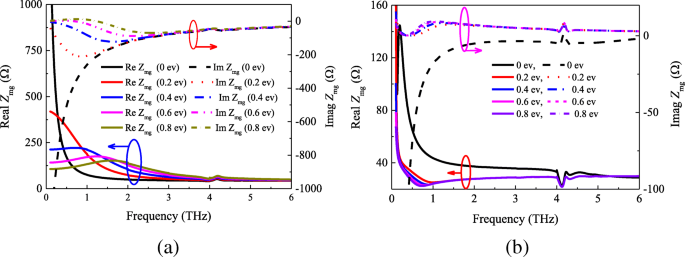
超表面-石墨烯薄膜阻抗Z mg 具有不同的化学势。 一 分析和b 模拟结果

从图 5a、b 可以看出，解析结果与模拟结果存在较大差异。图 5a 表明，分析结果的实部主要集中在 40 到 500 Ω 之间，有效阻抗的虚部范围从 - 210 到 0 Ω。尽管如此，根据图 5b，我们可以发现阻抗的实部值从 20 到 140 Ω，虚部随着 μ 的增加而接近于 0 c 从 0 到 0.8 ev。然而，分析和模拟结果显示出相同的趋势，即阻抗随着频率的增加而趋于稳定。原因是石墨烯片和方形贴片的阻抗随着频率的增加而变小。值得注意的是，将超表面-石墨烯薄膜在 0 ev 时的阻抗与其他结果进行比较，阻抗 Z 毫克完全不同。这是因为在 0 ev 时的石墨烯片阻抗值与较高的化学势有很大不同（见图 4）。

因此，我们可以从图 5 中计算和模拟的阻抗得出以下结论。 首先，超表面-石墨烯薄膜 Z 的表面阻抗 mg 并不严格等于 Z 的平行组合 m 和 Z G。但是，其次，它们之间存在一定的关系。为了证明这些结论，我们首先用不同的贴片尺寸模拟图 1 中所示的吸收器的结构。具有化学势μ的超表面-石墨烯吸收体的反射系数 c =0.4 ev 如图 6 所示。 根据传输线理论和模型，阻抗 Z 可以得到毫克。图 7 显示了检索阻抗 Z 的实部和虚部 mg 具有不同的贴片大小。根据图 7a，可以看到超表面 - 石墨烯薄膜的实部在开始时随着贴片长度 w 而减少 从 17 μm 增加到 19.5 μm。然而，当频率高于 0.31 THz 时，发现了相反的趋势。另一方面，图7b表明虚部的趋势与图7a的前半部分相同。此外，比较图。在图 4 和 5a 中，我们发现图 4 和 5a 中存在类似的情况。 3和7，也直接证明了上述结论。

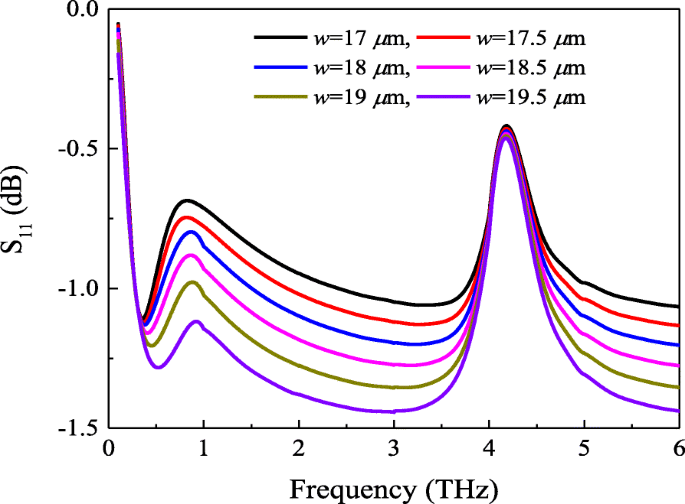
具有化学势μ的超表面-石墨烯吸收体的反射系数 c =0.4 ev

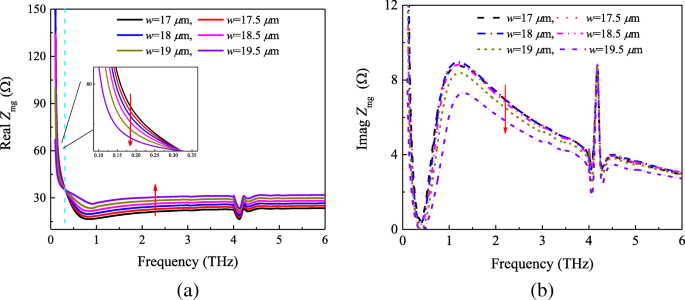
超表面-石墨烯薄膜阻抗Z 从 S 检索到的 mg -具有化学势μ的参数 c =0.4 ev。 一 真实和b 虚部

为了进一步探索作为贴片尺寸函数的表面电阻的物理起源，在 3 THz 处研究了超表面 - 石墨烯膜在垂直入射时的表面电流分布。图 8 显示了 w 的电流强度变化 =17、18 和 19 μm，化学势为 μ c =0.4ev。颜色代表场的强度。显然，随着尺寸的增加，表面电流的幅度减小。考虑到方程。由图 3 和图 7a 可知，当电场强度为 3 THz 固定值时，超表面-石墨烯的薄膜阻抗可由下式给出

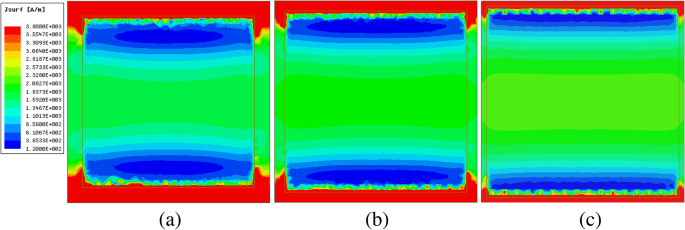
具有不同贴片尺寸但频率相同的表面电流大小。 一 w =17 微米，b w =18 μm 和 c w =19 微米

由式(11)可知，贴片的长度与表面电流J的大小成反比 .可以清楚地观察到模拟结果和理论结果之间的定性一致性。为了量化分析这种物理现象，使用HFSS场计算器计算了超表面-石墨烯薄膜表面电流分布的积分值，数值分别为1.10e-6、1.07e-6和1.04e-6 A ， 分别。这些结果与图8一致。

结论

总之，对于太赫兹频率的超表面-石墨烯薄膜，研究了基本和有效表面阻抗。推导出并验证了用于计算方形贴片阻抗的分析公式。对于超表面-石墨烯混合结构，将基于提取的反射系数的模拟结果与方形贴片和石墨烯片阻抗并联组合获得的分析结果进行比较。在讨论贴片尺寸对有效阻抗的影响时进行了额外的分析。此外，通过绘制和积分表面电流，定性和定量地解释了贴片尺寸和薄膜阻抗之间的关系。这种分析方法可以扩展到研究其他两个不同导电层的阻抗问题。此外，我们在这项工作中所做的分析可以避免大量的数值模拟以及分析优化专门应用于天线和吸收体的复合层。

缩写

HFSS：

高频结构仿真

TEM：

横向电磁

太赫兹：

太赫兹