简单串联共振

类似的效果发生在串联电感/电容电路中。当达到谐振状态（容抗和感抗相等）时，两个阻抗相互抵消，总阻抗降至零！ 示例：

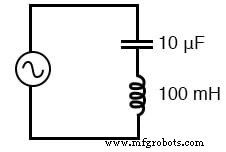
简单的串联谐振电路。

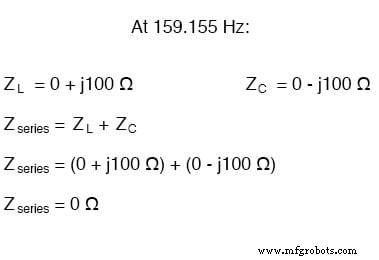
在 159.155 Hz 的谐振频率下，总串联阻抗等于 0 Ω，结果是短路 在谐振时跨越交流电源。在上面绘制的电路中，这不会很好。

我将添加一个与电容器和电感器串联的小电阻器（下图），以将最大电路电流限制在一定范围内，并在相同的频率范围内执行另一次 SPICE 分析。

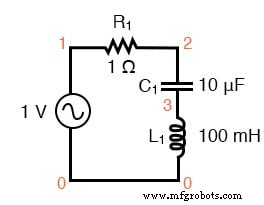
适用于 SPICE 的串联谐振电路。

串联lc电路 v1 1 0 交流 1 罪 r1 1 2 1 c1 2 3 10u l1 3 0 100m .ac 林 20 100 200 .plot ac i(v1) 。结尾 

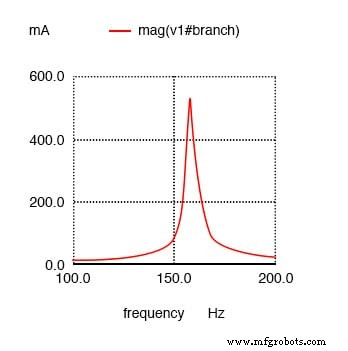
电流 I(v1) 的串联谐振电路图。

和以前一样，电路电流幅度从下到上增加，而频率从左到右增加。仍然可以看到峰值位于绘制的频率点 157.9 Hz，这是最接近我们预测的 159.155 Hz 共振点的分析点。

这表明我们的谐振频率公式对于简单的串联 LC 电路和简单的并联 LC 电路同样适用，就是这种情况：

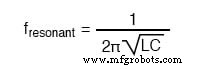
串联 LC 谐振电路需要注意：由于谐振时串联 LC 电路中可能存在高电流，因此可能会在电容器和电感器两端产生危险的高压降，因为每个组件都具有显着阻抗。

我们可以编辑上述示例中的 SPICE 网表，以包含电容器和电感器两端的电压图来演示发生的情况。

串联lc电路 v1 1 0 交流 1 罪 r1 1 2 1 c1 2 3 10u l1 3 0 100m .ac 林 20 100 200 .plot ac i(v1) v(2,3) v(3) 。结尾 

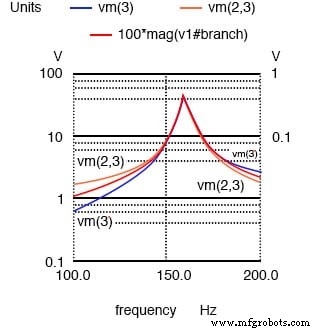
Vc=V(2,3) 70 V 峰值、VL=v(3) 70 V 峰值、I=I(V1#branch) 0.532 A 峰值的绘图.

根据 SPICE 的说法，电容器和电感器两端的电压在 70 伏左右达到峰值！

对于仅产生 1 伏电压的电源来说，这令人印象深刻。不用说，在试验这样的电路时要小心。由于 AC 分析语句 (.ac lin 20 100 200) 中的步数很小 (20)，因此 SPICE 电压低于预期值。期望值是多少？

给定：fr =159.155 Hz，L =100mH，R =1 XL =2πfL =2π(159.155)(100mH)=j100Ω XC =1/(2πfC) =1/(2π(159.155)(10µF)) =-j100Ω Z =1 +j100 -j100 =1 Ω I =V/Z =(1 V)/(1 Ω) =1 A VL =IZ =(1 A)(j100) =j100 V VC =IZ =(1 A)(-j100) =-j100 V VR =IR =(1 A)(1)=1 V Vtotal =VL + VC + VR Vtotal =j100 -j100 +1 =1 V 

电容器和电感器电压的预期值为 100 V。该电压会将这些组件施加到该水平，因此必须对其进行相应的额定。然而，这些电压是异相的并相互抵消，从而在所有三个分量上产生的总电压仅为 1 V，即施加电压。电容（或电感）电压与外加电压之比为“Q”因数。

 Q =VL/VR =VC/VR

评论：

• 当电源频率接近谐振时，串联 LC 电路的总阻抗接近于零。
• 用于确定简单谐振电路中谐振频率的相同公式也适用于简单串联电路。
• 在谐振时，串联 LC 电路的各个组件之间可能会形成极高的电压，这是由于高电流和大量的单个组件阻抗。

相关工作表：

• 串联和并联交流电路工作表