驻波和共振

只要传输线和负载之间的阻抗不匹配，就会发生反射。如果入射信号是连续的交流波形，这些反射将与更多的迎面而来的入射波形混合，产生称为驻波的固定波形 .

下图显示了三角形的入射波形在到达线路的未端接端时如何变成镜像反射。为简单起见，此说明性序列中的传输线显示为单条粗线，而不是一对导线。

入射波从左向右传播，反射波从右向左传播：（下图）

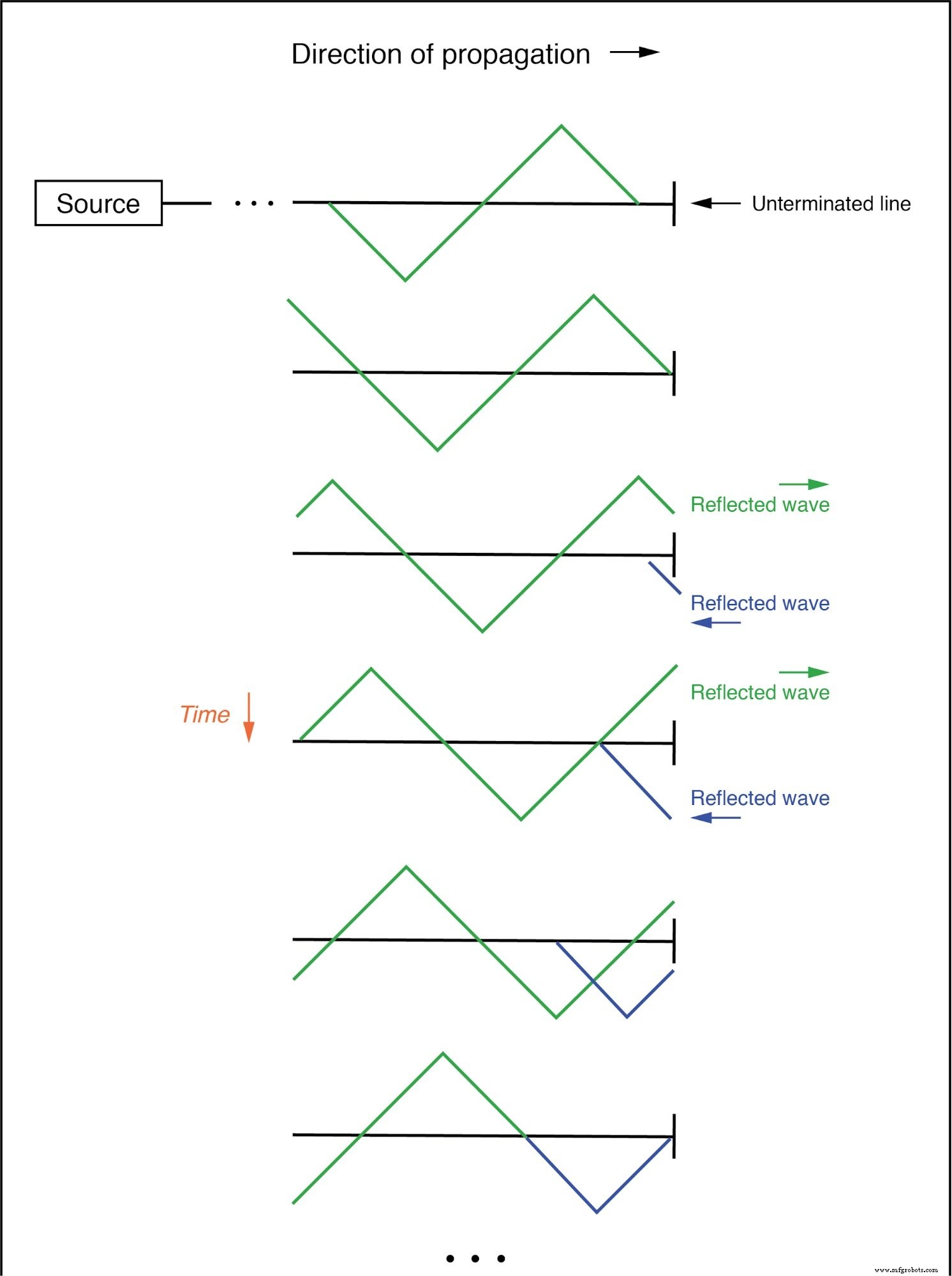
入射波在未端接传输线的末端反射。

如果我们将两个波形加在一起，我们会发现沿着线的长度创建了第三个固定波形：（下图）

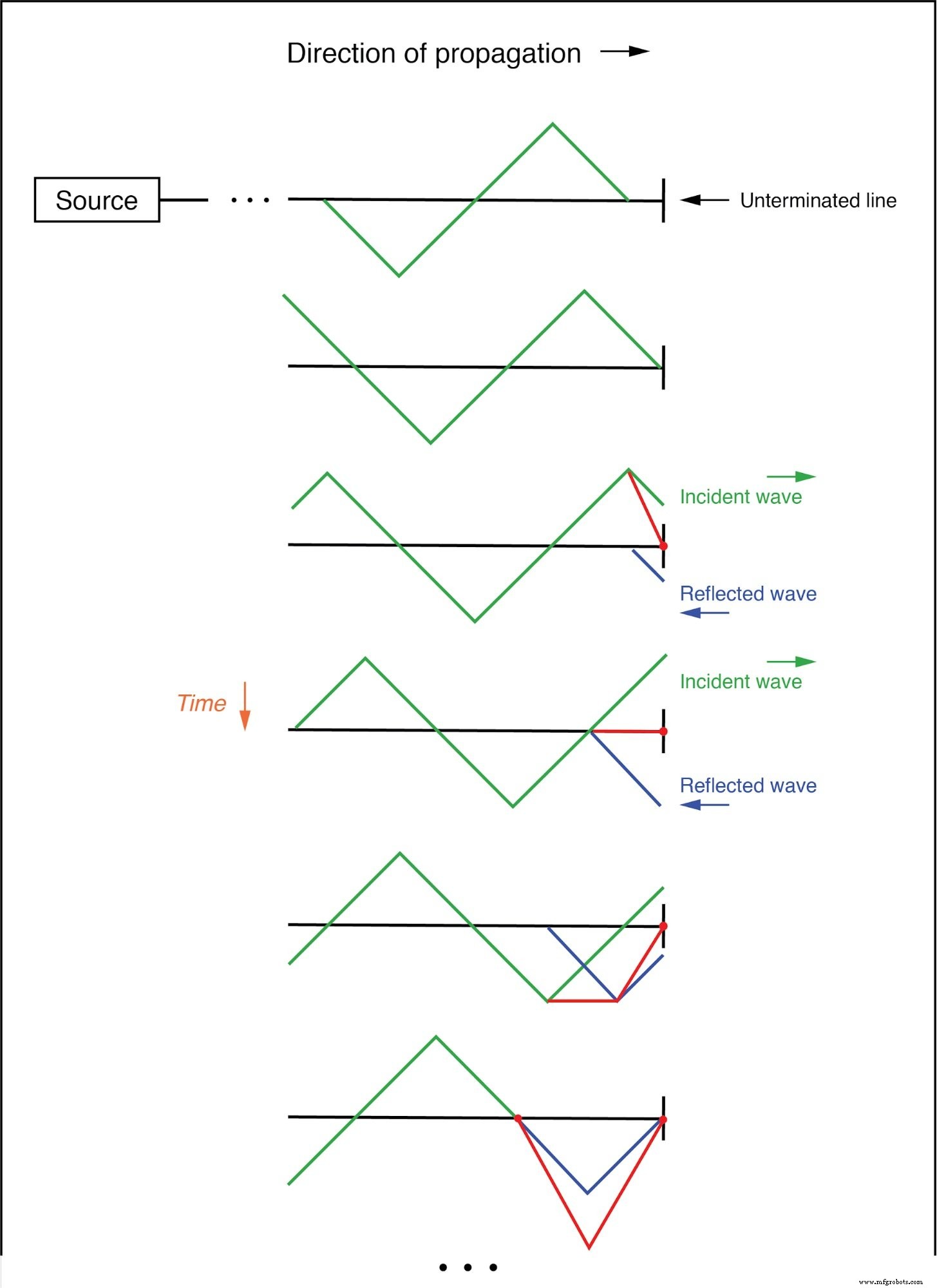
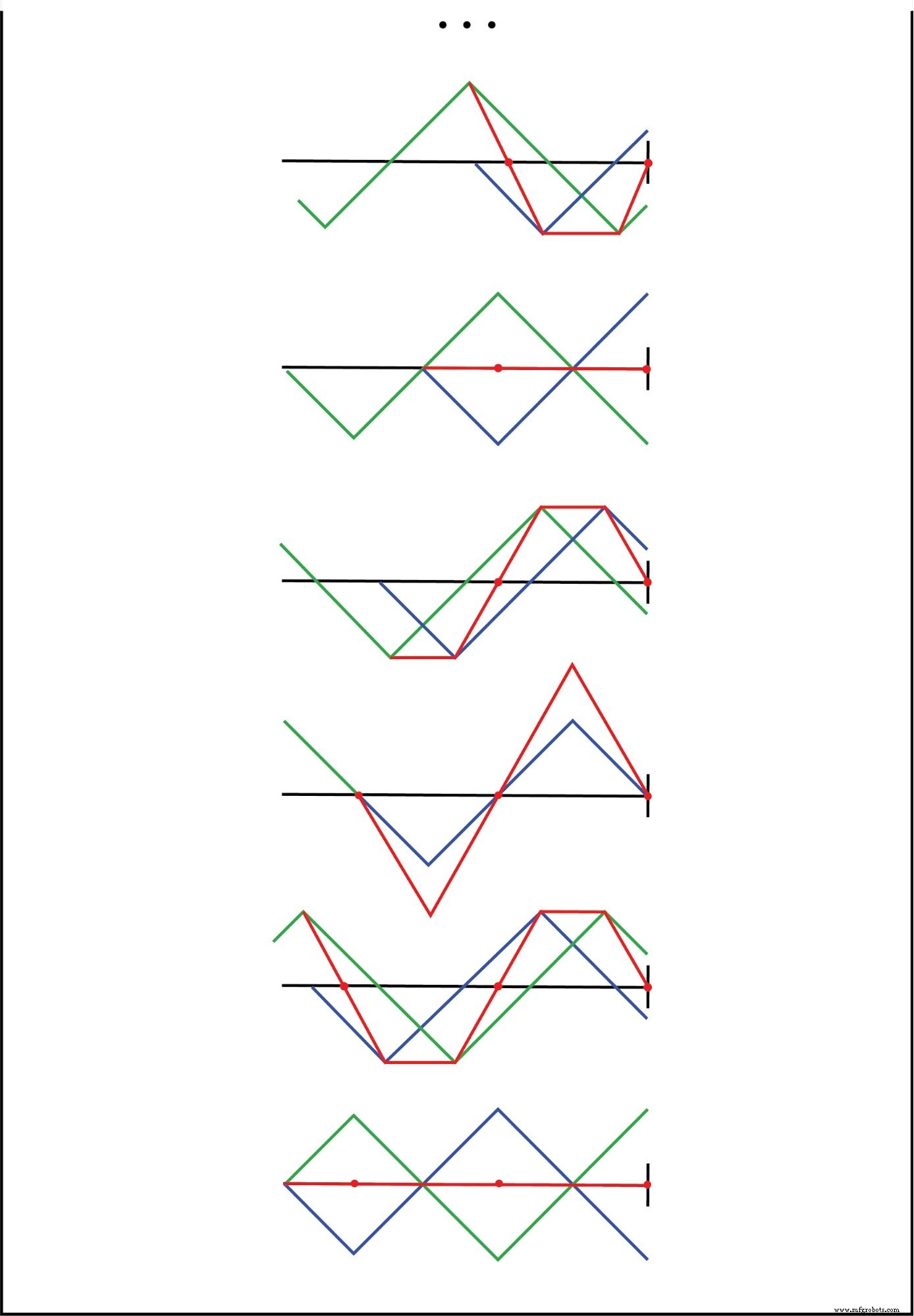
入射波和反射波的总和是驻波。

这第三个“驻波”实际上代表了沿线的唯一电压，它是入射和反射电压波的代表总和。它以瞬时幅度振荡，但不会像引起它的入射或反射波形那样沿电缆长度传播。

注意沿线长度的点标记驻波的“零”点（入射波和反射波相互抵消），以及这些点如何永远不会改变位置：（下图）

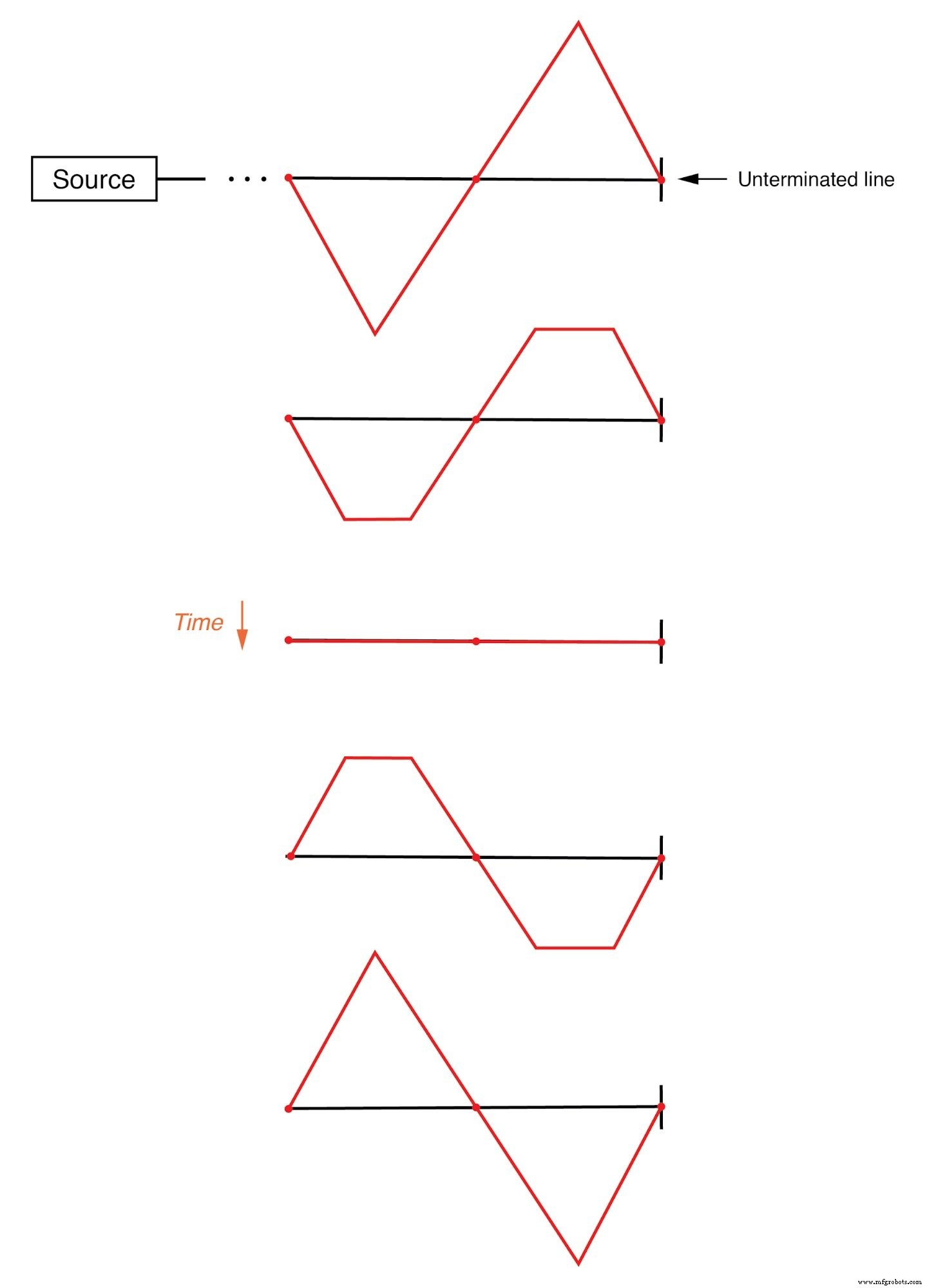
驻波不沿传输线传播。

产生驻波的情况

驻波在物理世界中非常丰富。考虑一根绳子或绳子，一端摇动，另一端系住（仅显示手部运动的一个半周期，向下移动）：（下图）

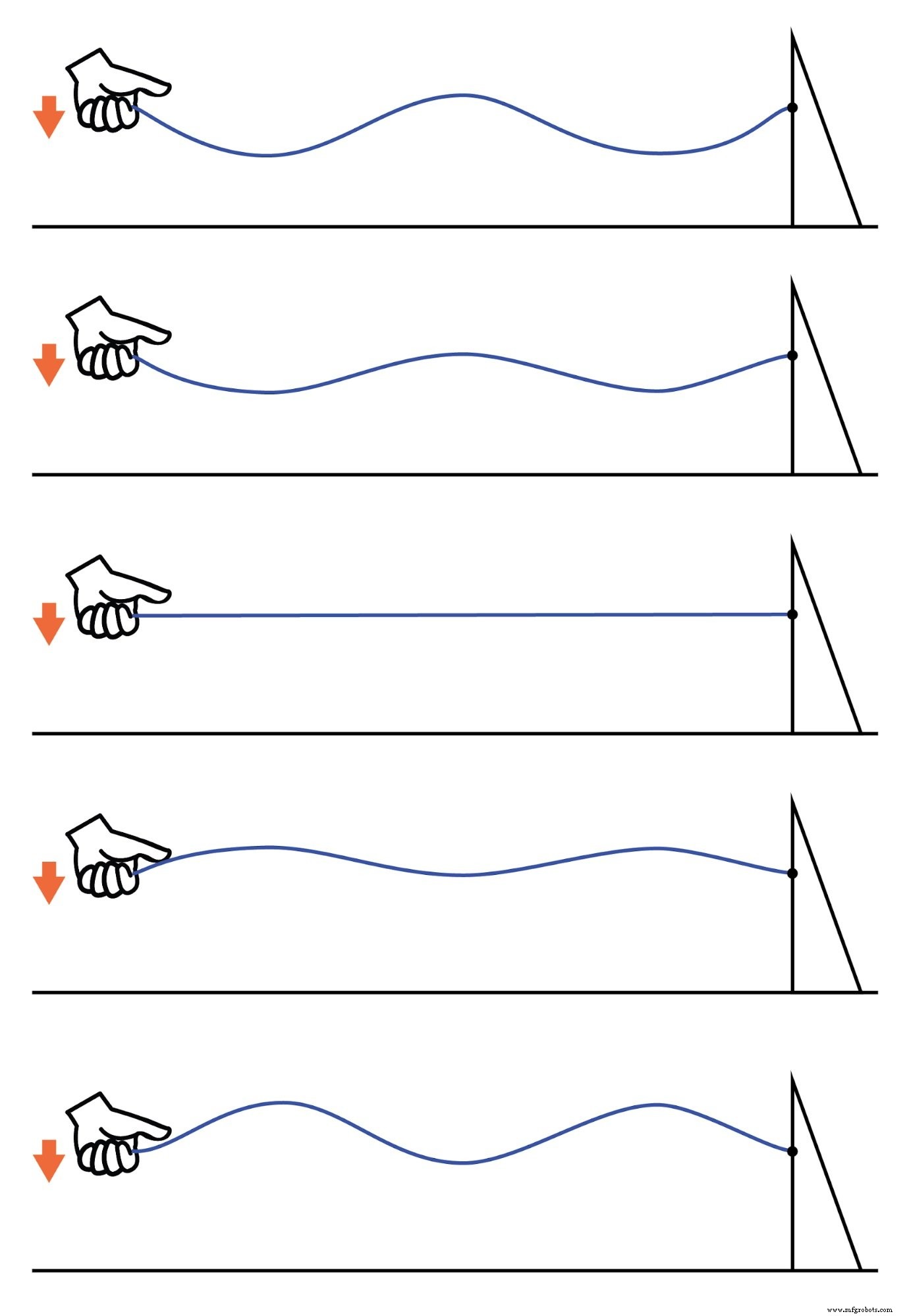
绳索上的波浪。

节点（振动很小或没有振动的点）和波腹（振动最大的点）沿弦或绳的长度保持固定。

当自由端以恰到好处的频率震动时，效果最为明显。弹拨弦表现出相同的“驻波”行为，沿其长度具有最大和最小振动的“节点”。

弹拨和颤动的主要区别在于，弹拨提供了自己“正确”的振动频率，以最大限度地发挥驻波效应：（下图）

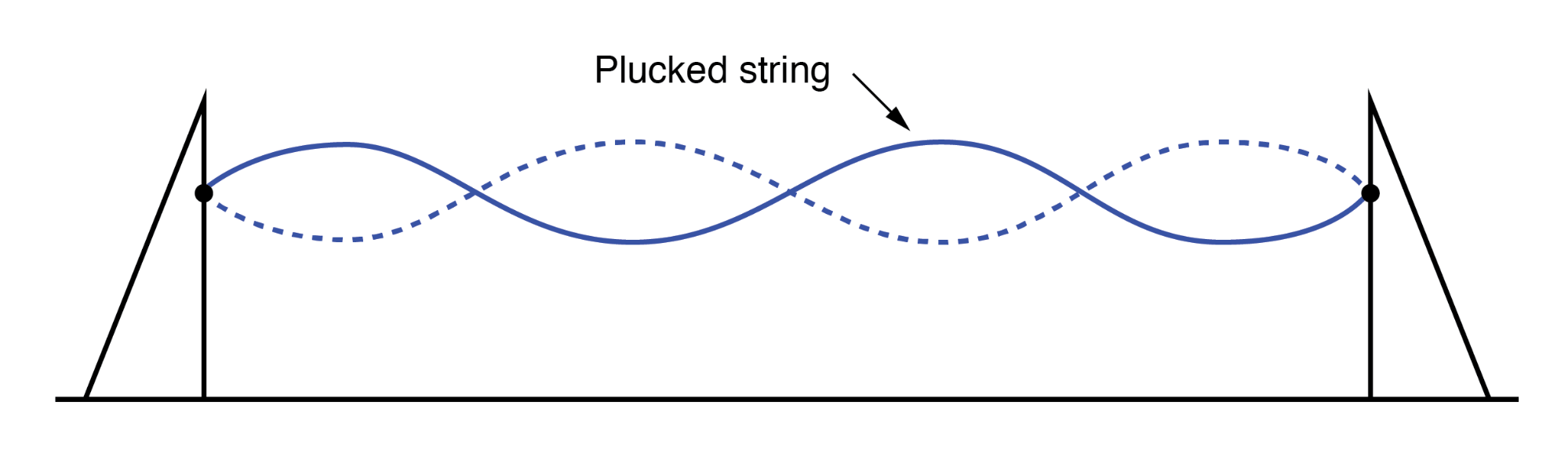
拨弦上的驻波。

吹过开口管的风也会产生驻波；这一次，波是管内空气分子（声音）的振动，而不是固体物体的振动。驻波终止于一个节点（最小振幅）还是一个波腹（最大振幅）取决于管的另一端是打开还是关闭：（下图）

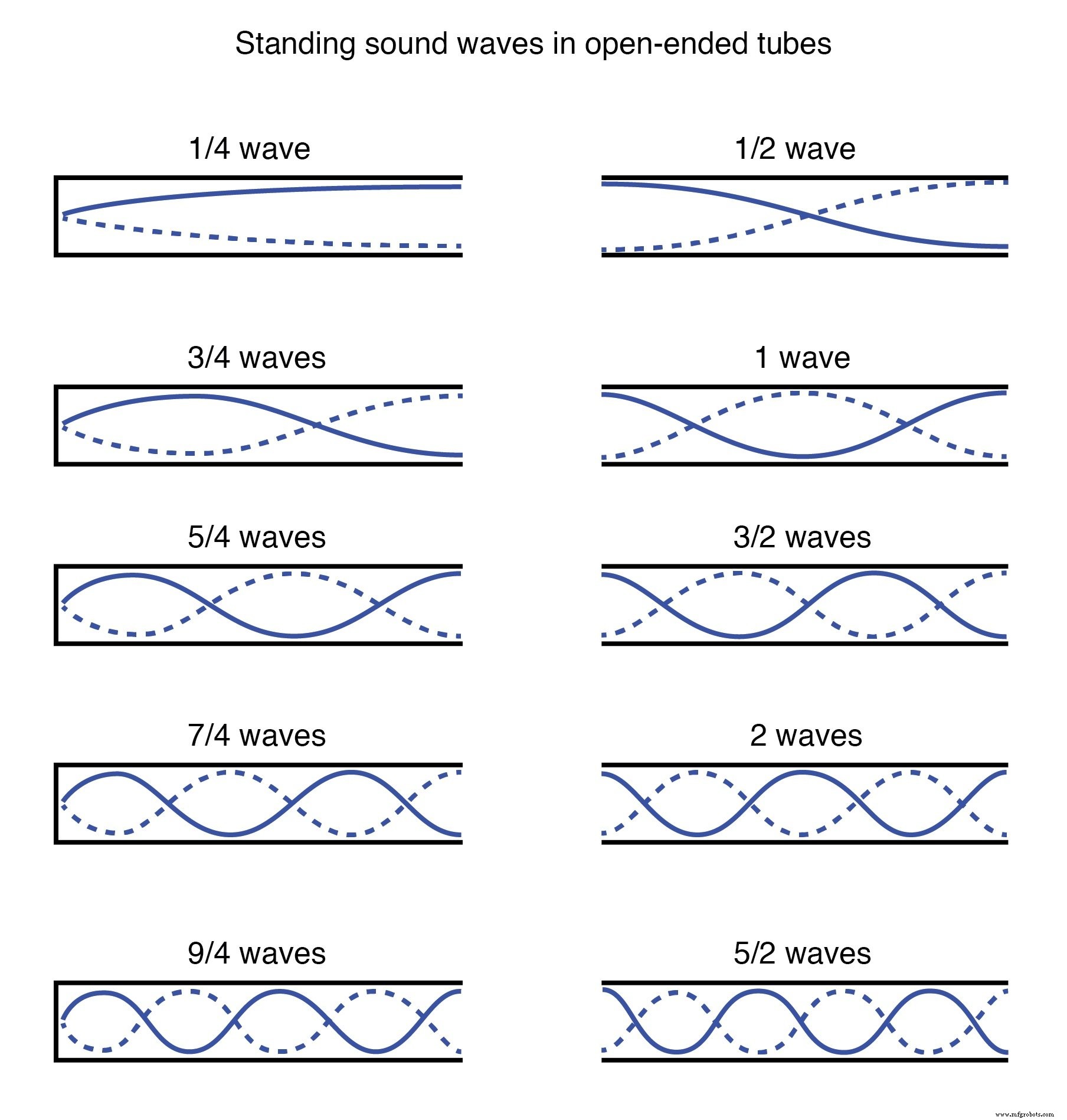
开口管中的声波。

封闭的管端必须是波节，而开放的管端必须是波腹。以此类推，振动弦的锚定端一定是一个节点，而自由端（如果有的话）一定是一个波腹。

谐振频率谐波的进展

请注意，如何有不止一种波长适合在管内产生与管端点精确匹配的振动空气驻波。

对于所有驻波系统都是如此：对于与系统的节点/波腹点相关的任何频率（波长），驻波将与系统共振。另一种说法是，任何支持驻波的系统都有多个谐振频率。

所有较高的频率都是系统最低（基本）频率的整数倍。谐波从一个谐振频率到下一个谐振频率的顺序进程定义了泛音 系统频率：（下图）

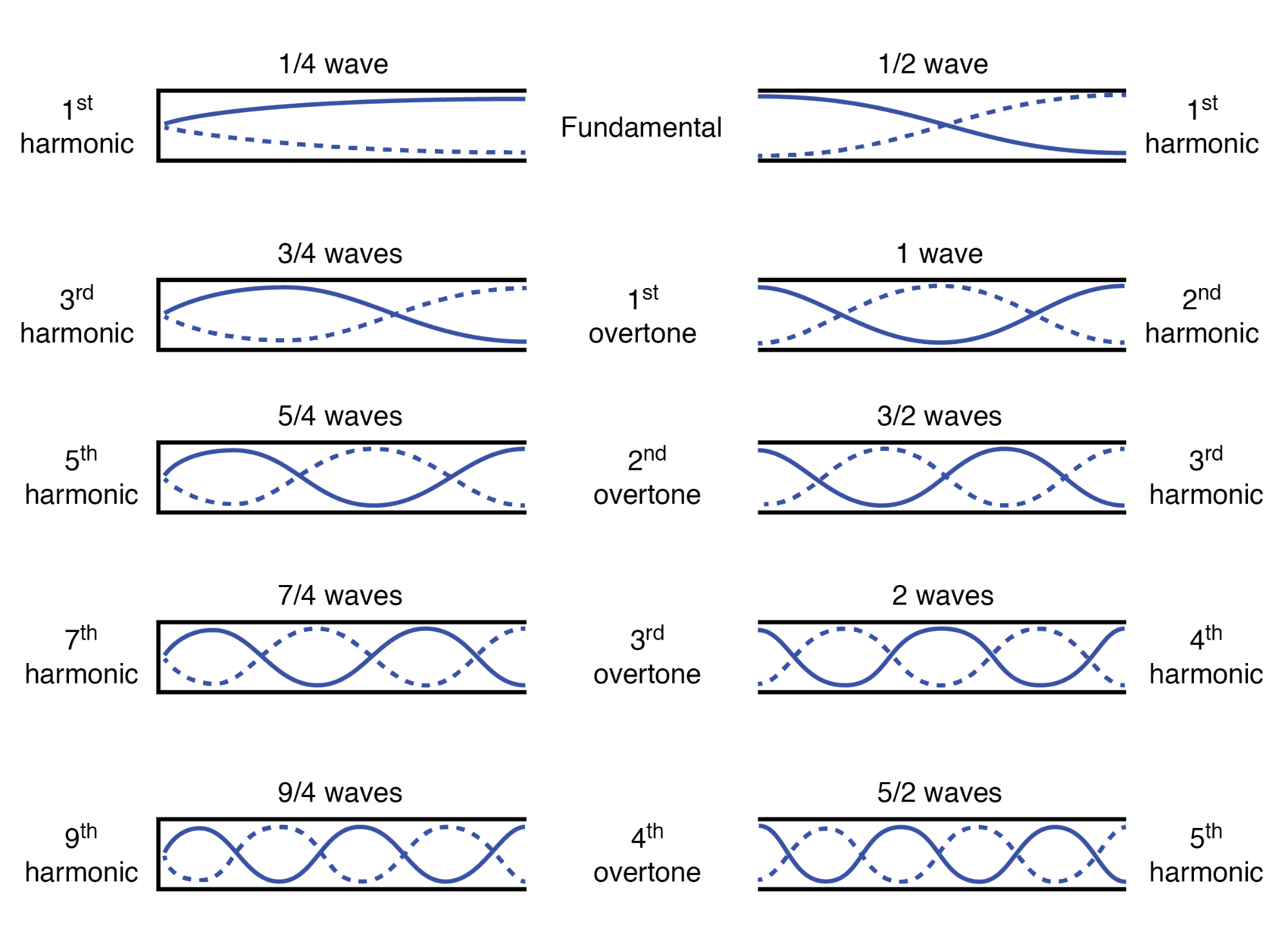
开口管中的谐波（泛音）

任何这些谐波或泛音的实际频率（以赫兹为单位）取决于管的物理长度和波的传播速度，即空气中的声速。

使用 SPICE 模拟传输线谐振

由于传输线支持驻波，并根据负载端的终端阻抗类型迫使这些波具有节点和波腹，因此它们也会在由物理长度和传播速度决定的频率下表现出共振。

然而，传输线谐振比琴弦或管内空气的谐振要复杂一些，因为我们必须同时考虑电压波和电流波。

通过计算机模拟，可以更容易地理解这种复杂性。首先，让我们检查一个完美匹配的源、传输线和负载。所有组件的阻抗为 75 Ω：（下图）

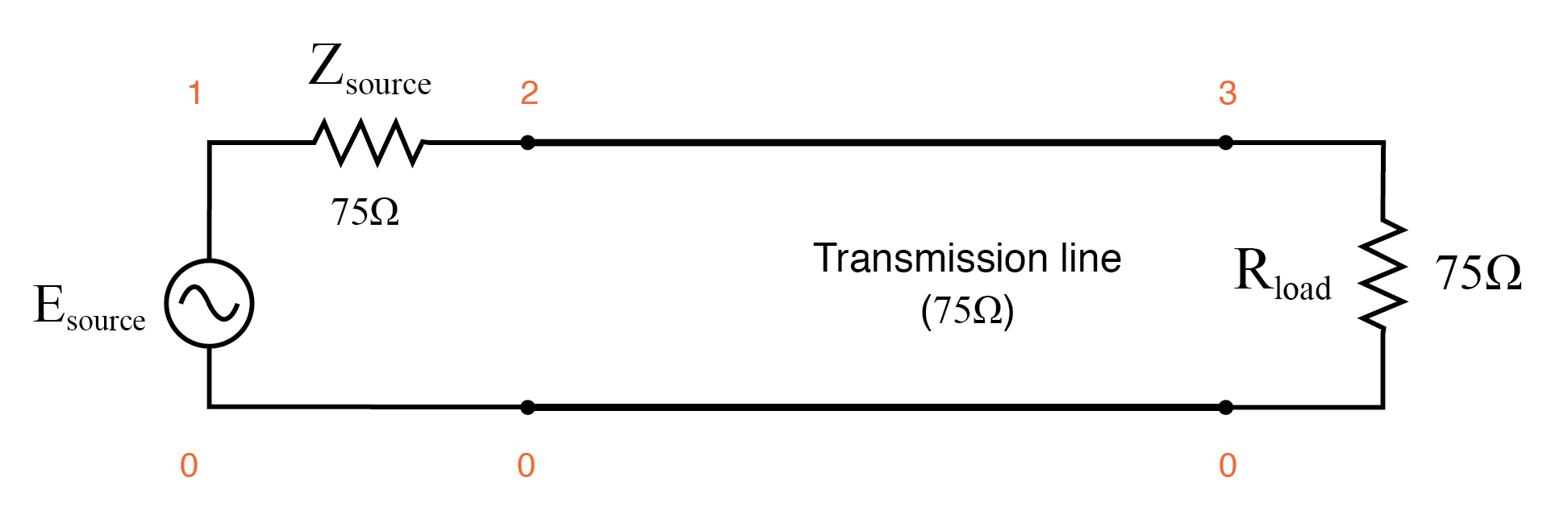
完美匹配的传输线。

使用 SPICE 来模拟电路，我们将指定传输线 (t1 ) 具有 75 Ω 特性阻抗 (z0=75 ) 和 1 微秒的传播延迟 (td=1u ）。这是表示传输线物理长度的一种方便的方法：波沿其整个长度传播所需的时间。

如果这是一根真正的 75 Ω 电缆——也许是“RG-59B/U”型同轴电缆，通常用于有线电视分配的类型——速度系数为 0.66，它大约有 648 英尺长。

由于 1 µs 是 1 MHz 信号的周期，我将选择从（接近）零到该数字扫描交流电源的频率，以查看系统在暴露于从直流到 1 个波长的信号时如何反应。

这是上图所示电路的 SPICE 网表：

传输线 v1 1 0 交流 1 罪 资源 1 2 75 t1 2 0 3 0 z0=75 td=1u 加载 3 0 75 .ac lin 101 1m 1meg * 使用“Nutmeg”程序进行绘图分析 。结尾 

运行此仿真并绘制源阻抗下降（作为电流指示）、源电压、线路的源端电压和负载电压，我们看到源电压——显示为 vm(1)（电压幅值之间的图上的节点 1 和节点 0 的隐含接地点）—记录稳定的 1 伏，而每隔一个电压记录稳定的 0.5 伏：（下图）

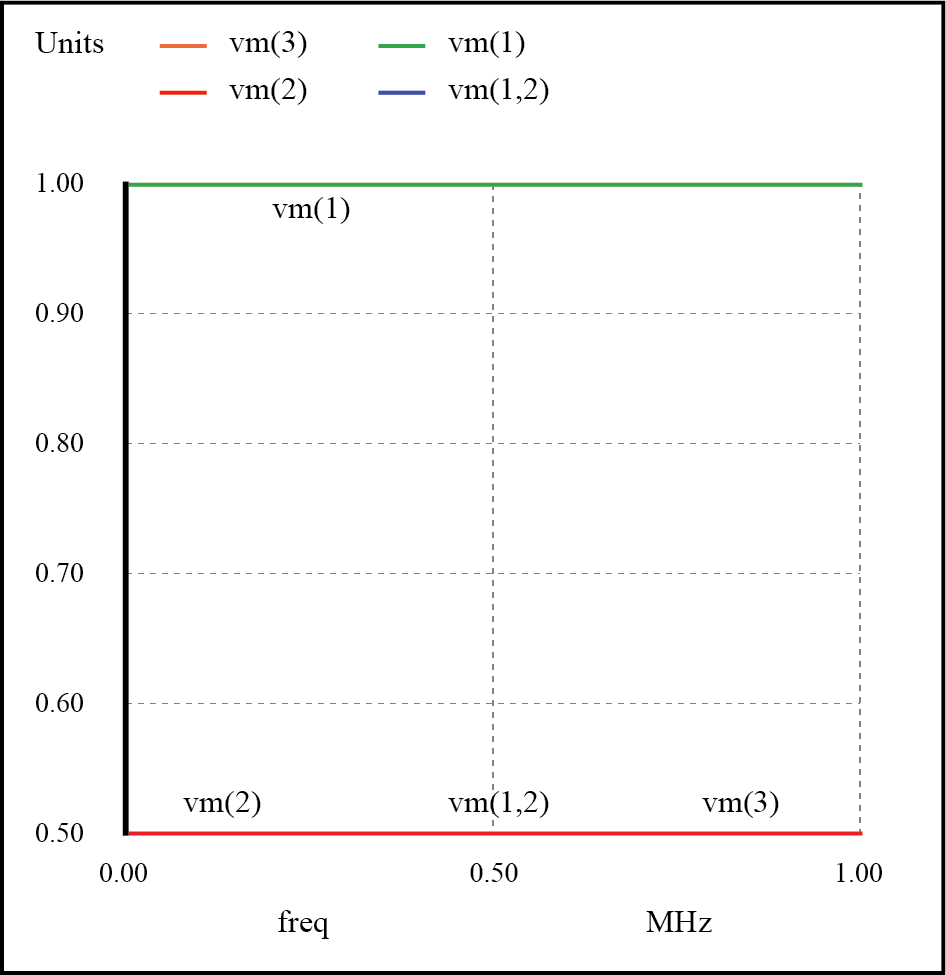
匹配的传输线上没有共振。

在所有阻抗完全匹配的系统中，不可能有驻波，因此在波德图中没有谐振“峰”或“谷”。

现在，让我们将负载阻抗更改为 999 MΩ，以模拟开端传输线。 （下图）当频率从 1 mHz 扫到 1 MHz 时，我们现在肯定会看到线​​路上的一些反射：（下图）

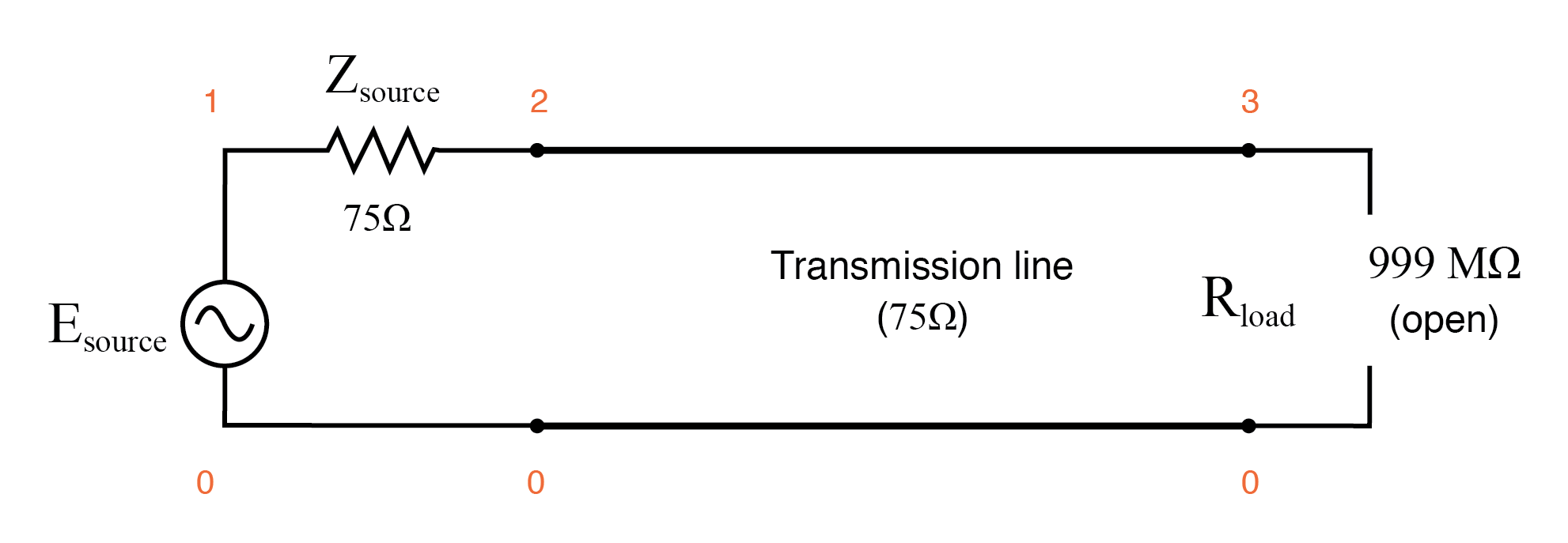
开放式传输线。

传输线 v1 1 0 交流 1 罪 资源 1 2 75 t1 2 0 3 0 z0=75 td=1u 加载 3 0 999meg .ac lin 101 1m 1meg * 使用“Nutmeg”程序进行绘图分析 。结尾 

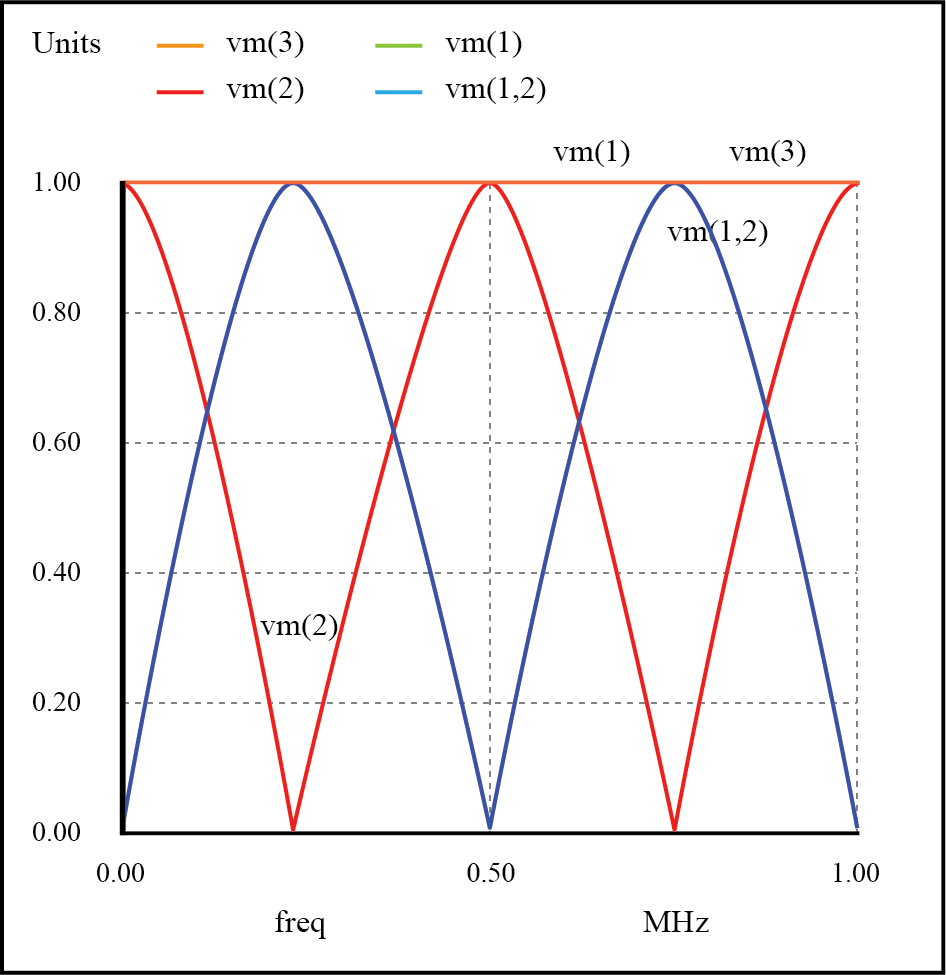
开放传输线上的共振。

这里，电源电压 vm(1) 和线路的负载端电压 vm(3) 保持稳定在 1 伏。其他电压在1 mHz至1 MHz的扫描范围内在不同频率处出现波峰和波峰。

沿着分析的水平轴有五个感兴趣的点：0 Hz、250 kHz、500 kHz、750 kHz 和 1 MHz。我们将研究每个电路不同点的电压和电流。

在 0 Hz（实际上是 1 mHz）时，信号实际上是直流的，并且电路的行为与给定 1 伏直流电池电源时的表现非常相似。

没有电路电流，如源阻抗上的零压降所示 (Zsource:vm(1,2) )，以及传输线源端的全源电压（节点 2 和节点 0 之间测量的电压：vm(2) ）。 （下图）

在f=0：输入：V=1，I=0；结束：V=1，I=0。

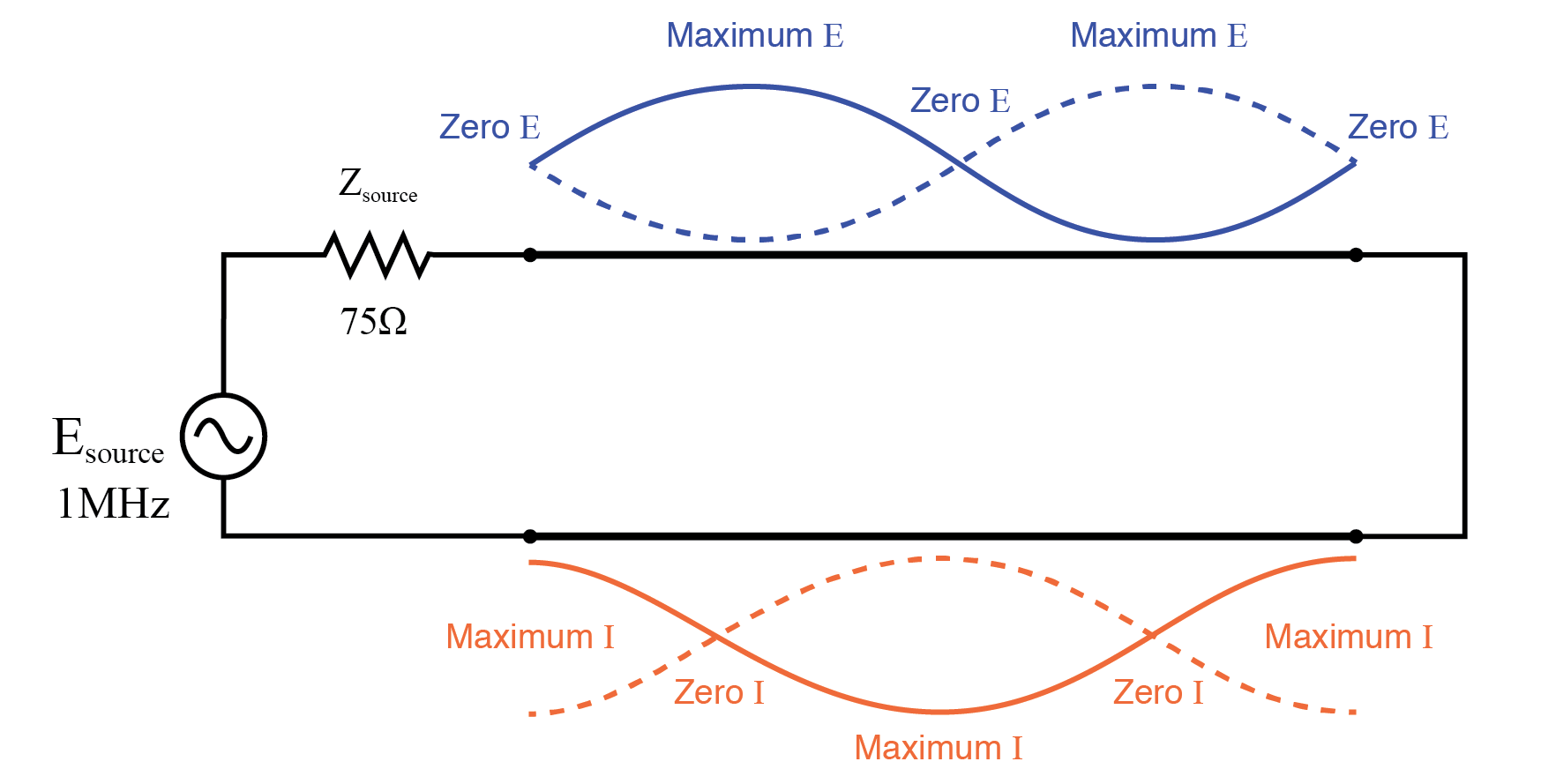
在 250 kHz 时，我们看到传输线源端电压为零，电流最大，但负载端仍为全电压：（下图）

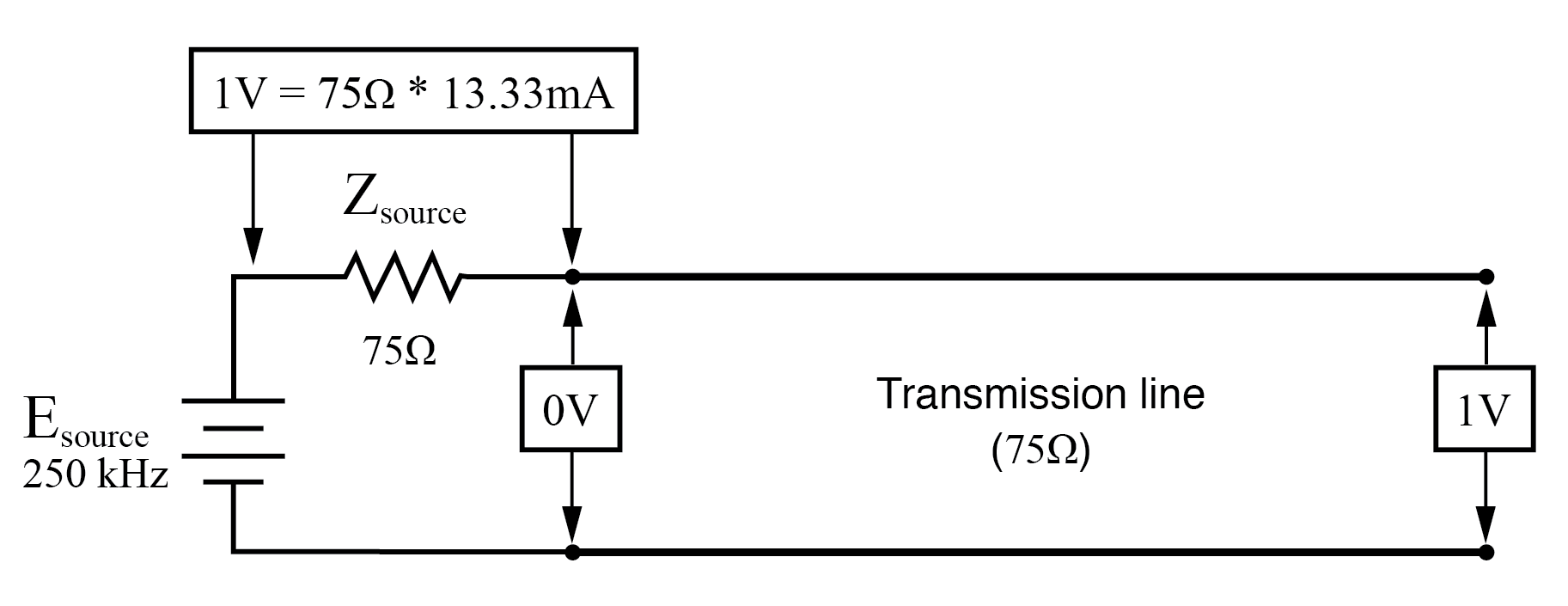
在 f=250 KHz 时：输入：V=0，I=13.33 mA；结束：V=1 I=0。

你可能想知道，这怎么可能？如何在线路入口处零电压的情况下，在线路的开放端获得全源电压？

答案可以在驻波悖论中找到。源频率为 250 kHz，线的长度正好适合 1/4 波长从头到尾拟合。线路负载端开路，可以没有电流，但是会有电压。

因此，开路传输线的负载端是电流节点（零点）和电压波腹（最大振幅）：（下图）

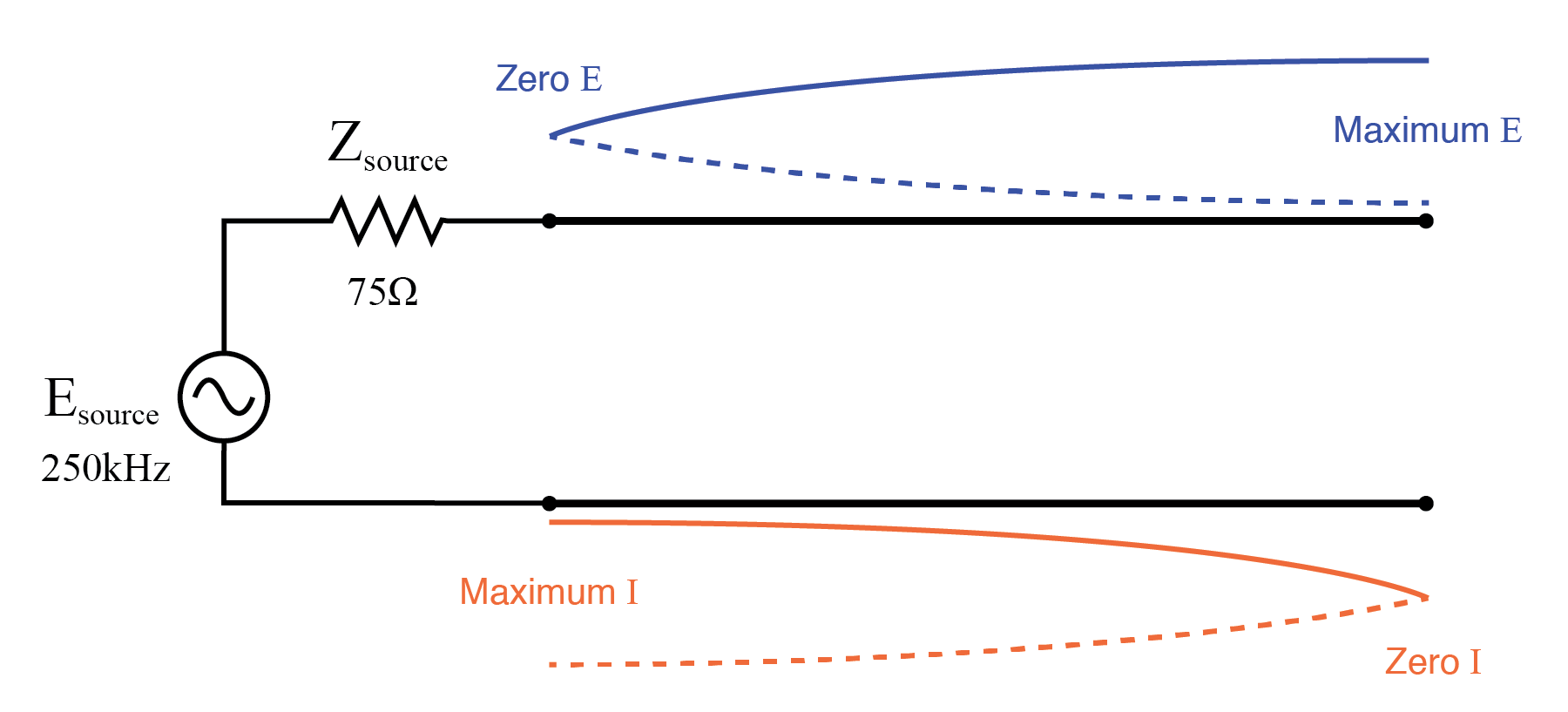
传输线开口端显示电流节点，开口端电压波腹。

在 500 kHz 时，驻波的一半正好位于传输线上，在这里我们看到分析中的另一点，源电流下降到零，传输线的源端电压再次上升到全电压：（下图）

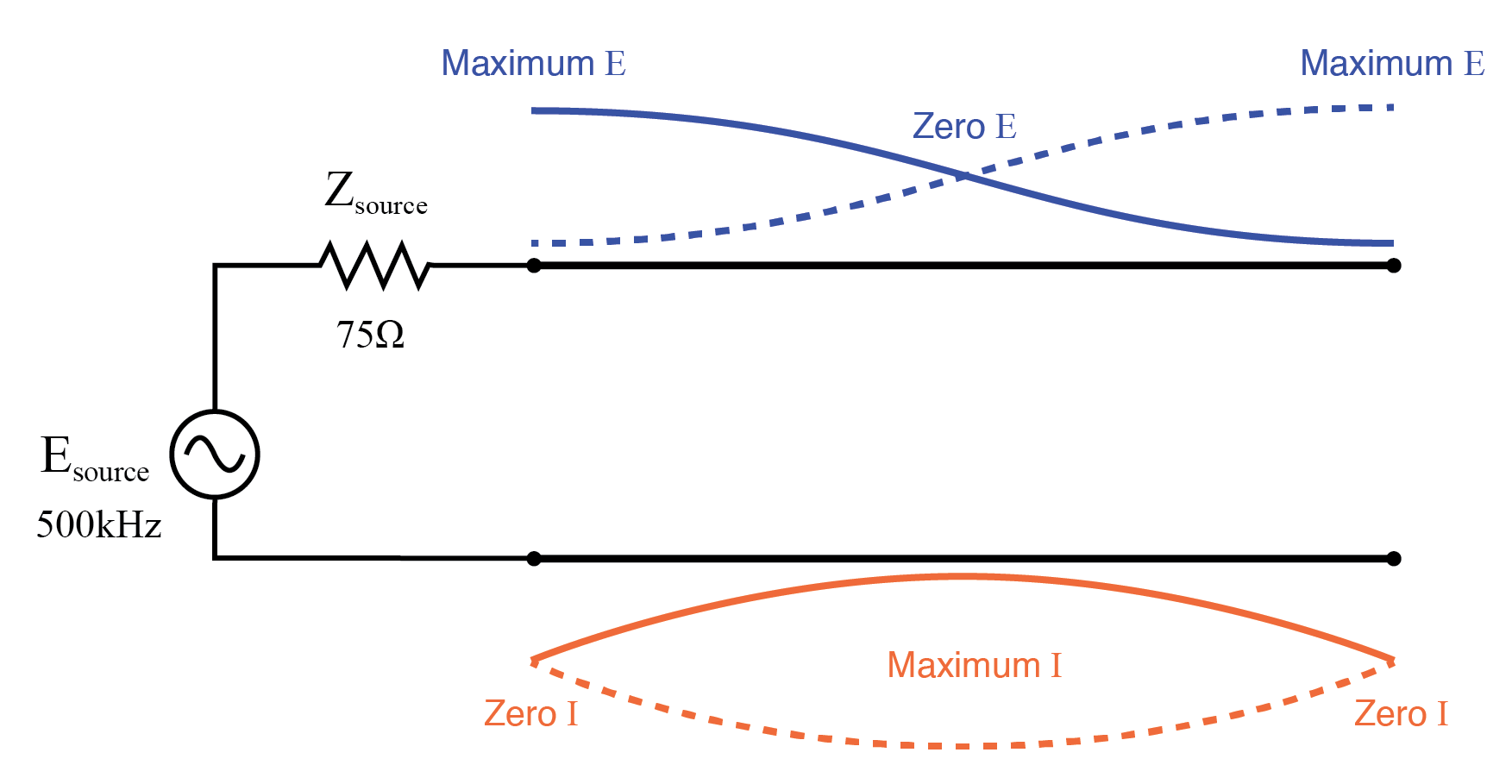
半波开放传输线上的全驻波。

在 750 kHz 时，该图看起来很像在 250 kHz 时：零源端电压 (vm(2)) 和最大电流 (vm(1,2))。这是由于 3/4 的波沿传输线保持平衡，导致源“看到”它连接到传输线的短路，即使线的另一端是开路的：（图下面）

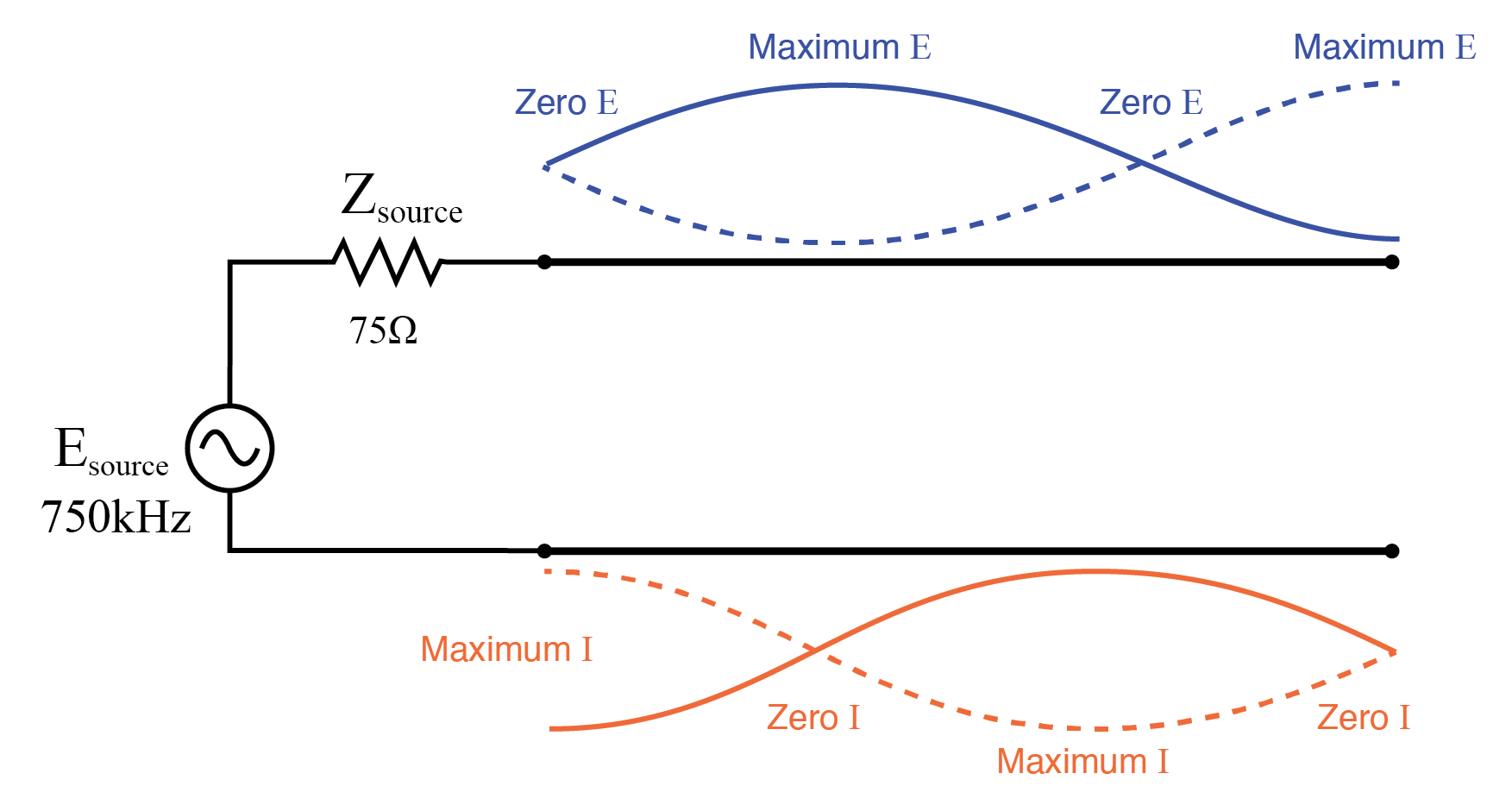
3/4 波开放传输线上的 1 1/2 驻波。

当电源频率扫描到 1 MHz 时，传输线上存在全驻波。此时，线路的源端经历与负载端相同的电压和电流幅度：全电压和零电流。本质上，源“看到”了它连接到传输线的点处的开路。 （下图）

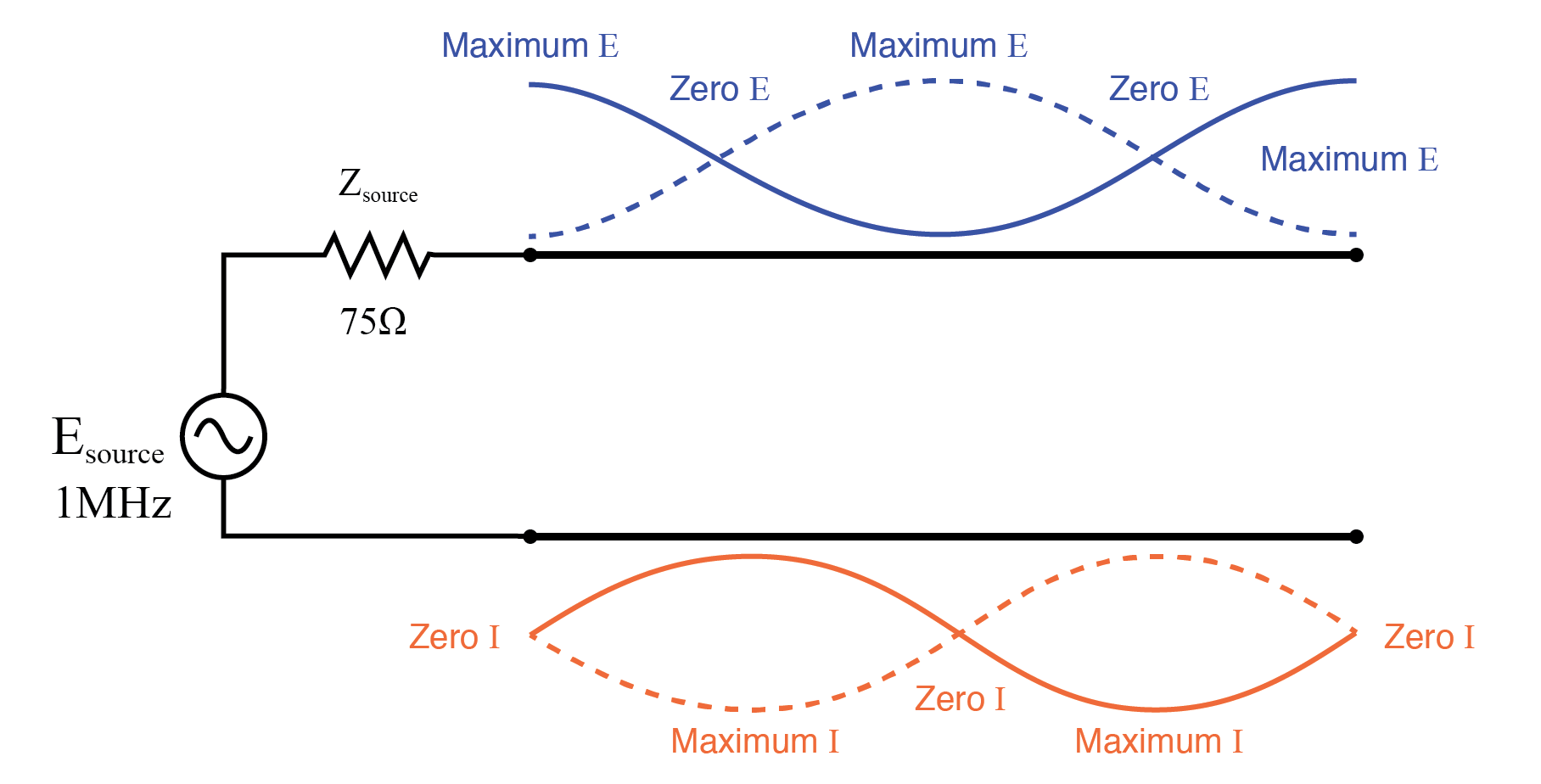
全波开放传输线上的双驻波。

以类似的方式，短路传输线会产生驻波，尽管电压和电流的节点和波腹分配相反：在线路的短路端，将有零电压（节点）和最大电流（波腹） .下面是 SPICE 模拟和所有有趣频率下发生的情况的说明：0 Hz、250 kHz、500 kHz、750 kHz 和 1 MHz。短路跳线由 1 µΩ 负载阻抗模拟：

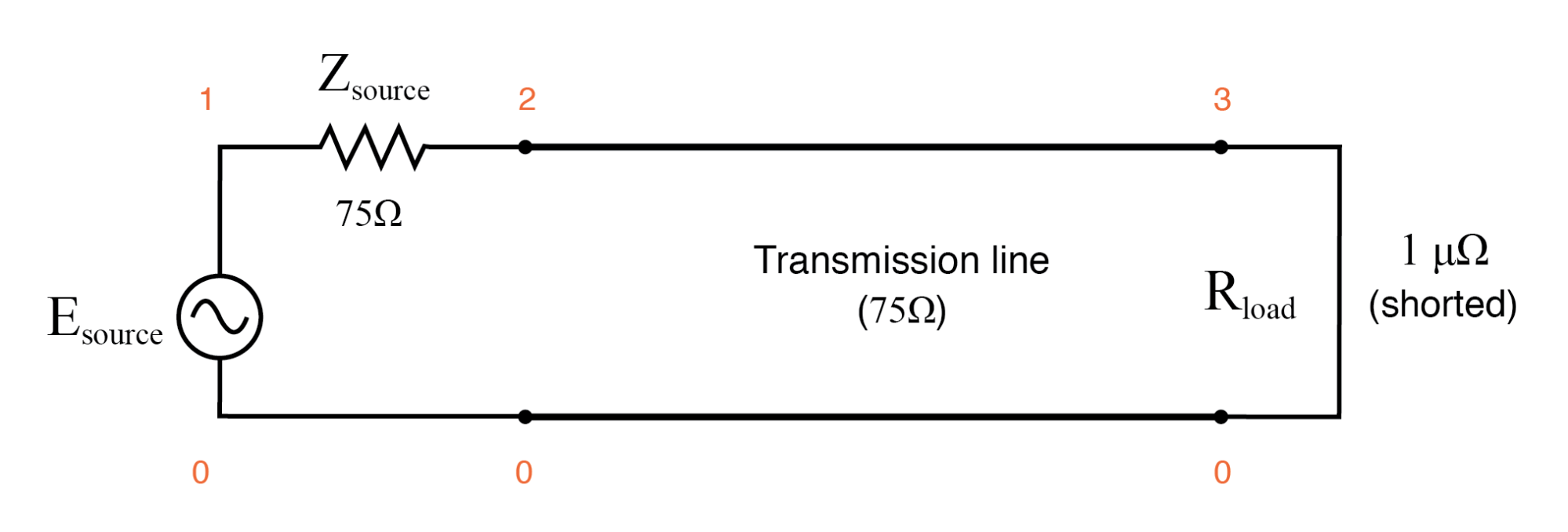
传输线短路。

传输线 v1 1 0 交流 1 罪 资源 1 2 75 t1 2 0 3 0 z0=75 td=1u 加载 3 0 1u .ac lin 101 1m 1meg * 使用“Nutmeg”程序进行绘图分析 。结尾 

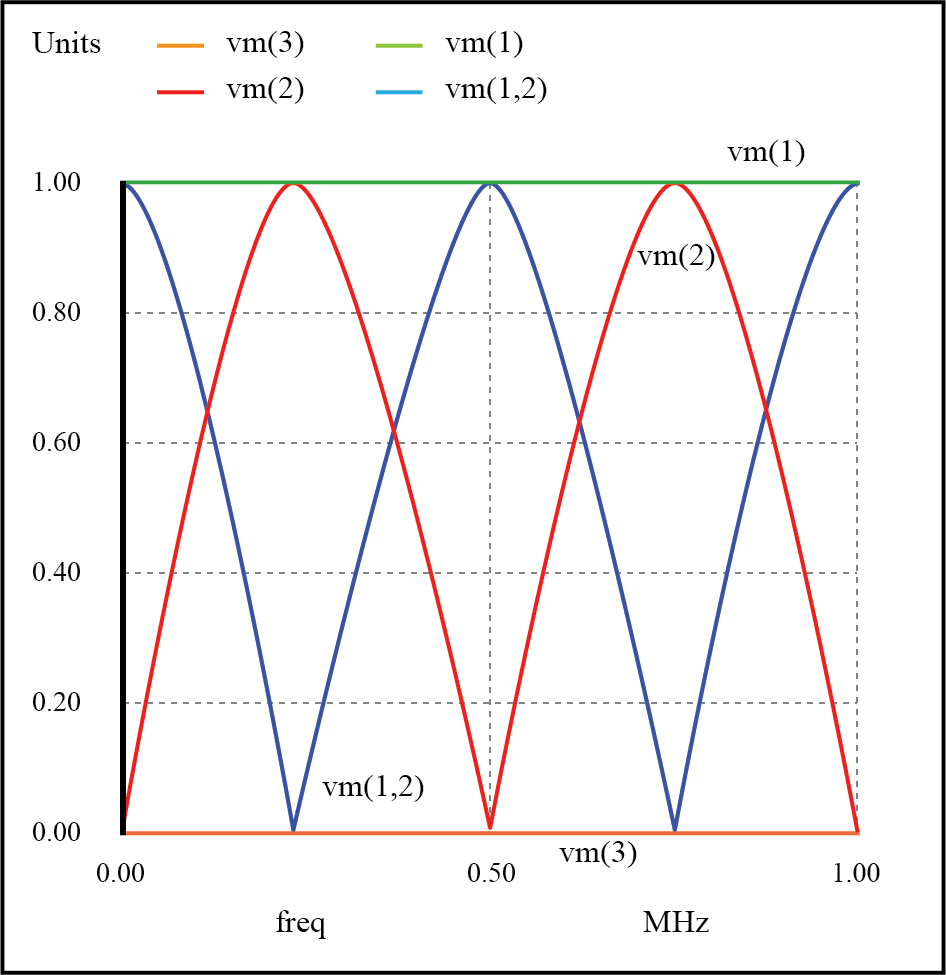
短路传输线的共振

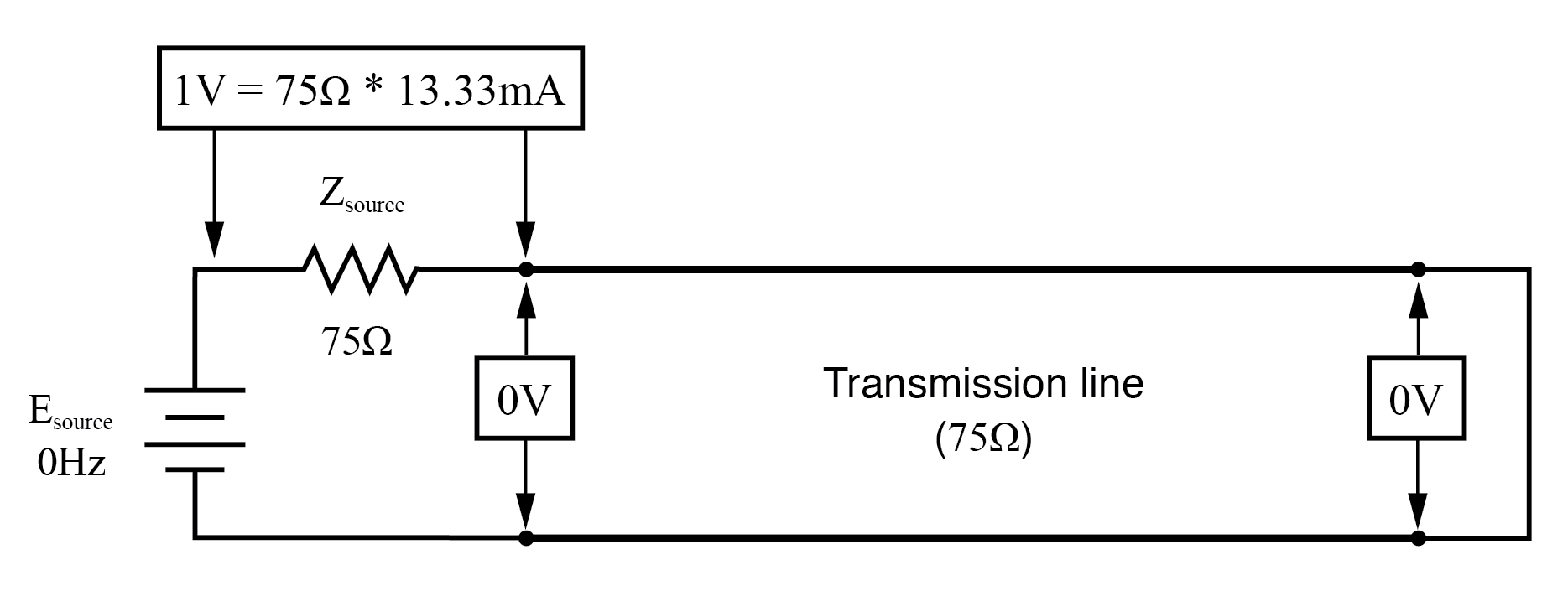
在 f=0 Hz 时：输入：V=0，I=13.33 mA；结束：V=0，I=13.33 mA。

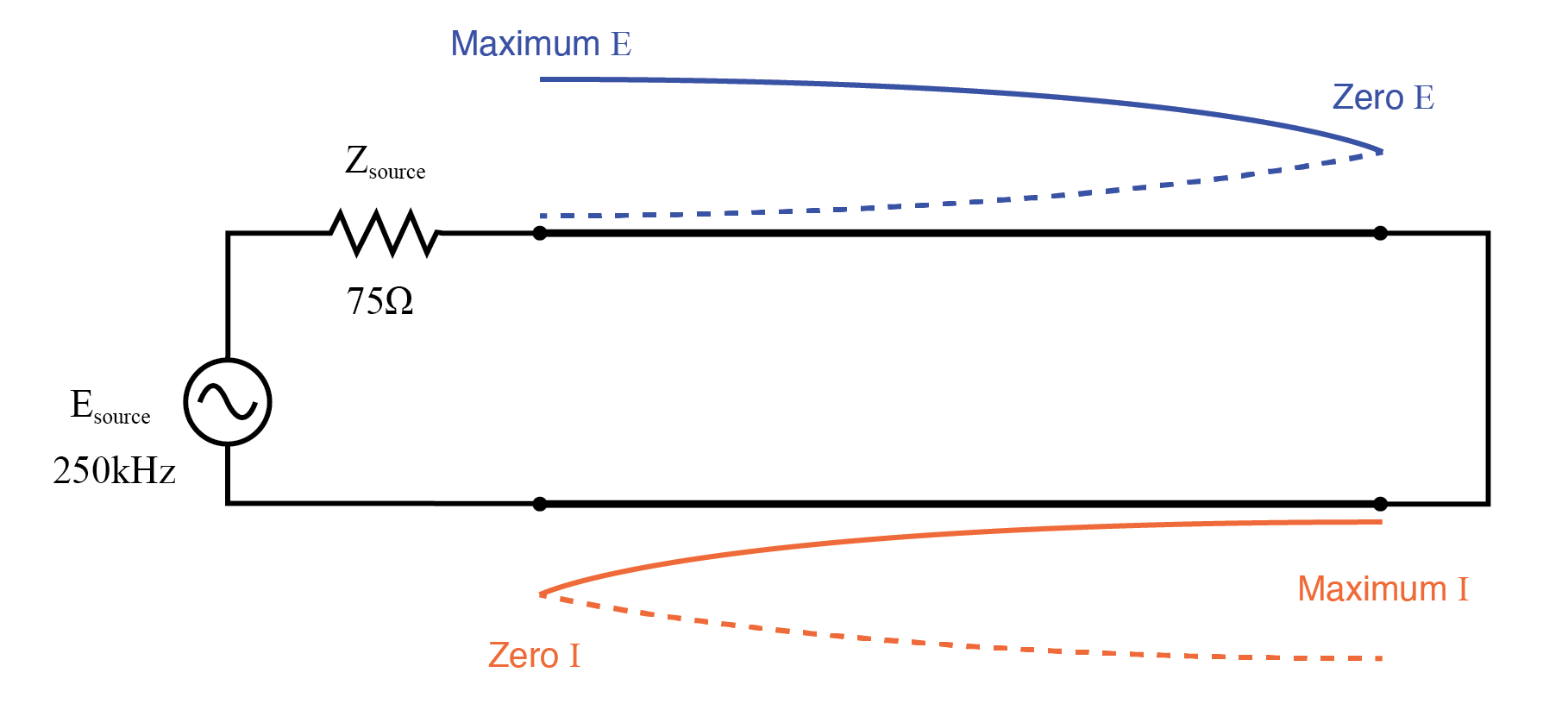
1/4 波短路传输线上的半波驻波模式。

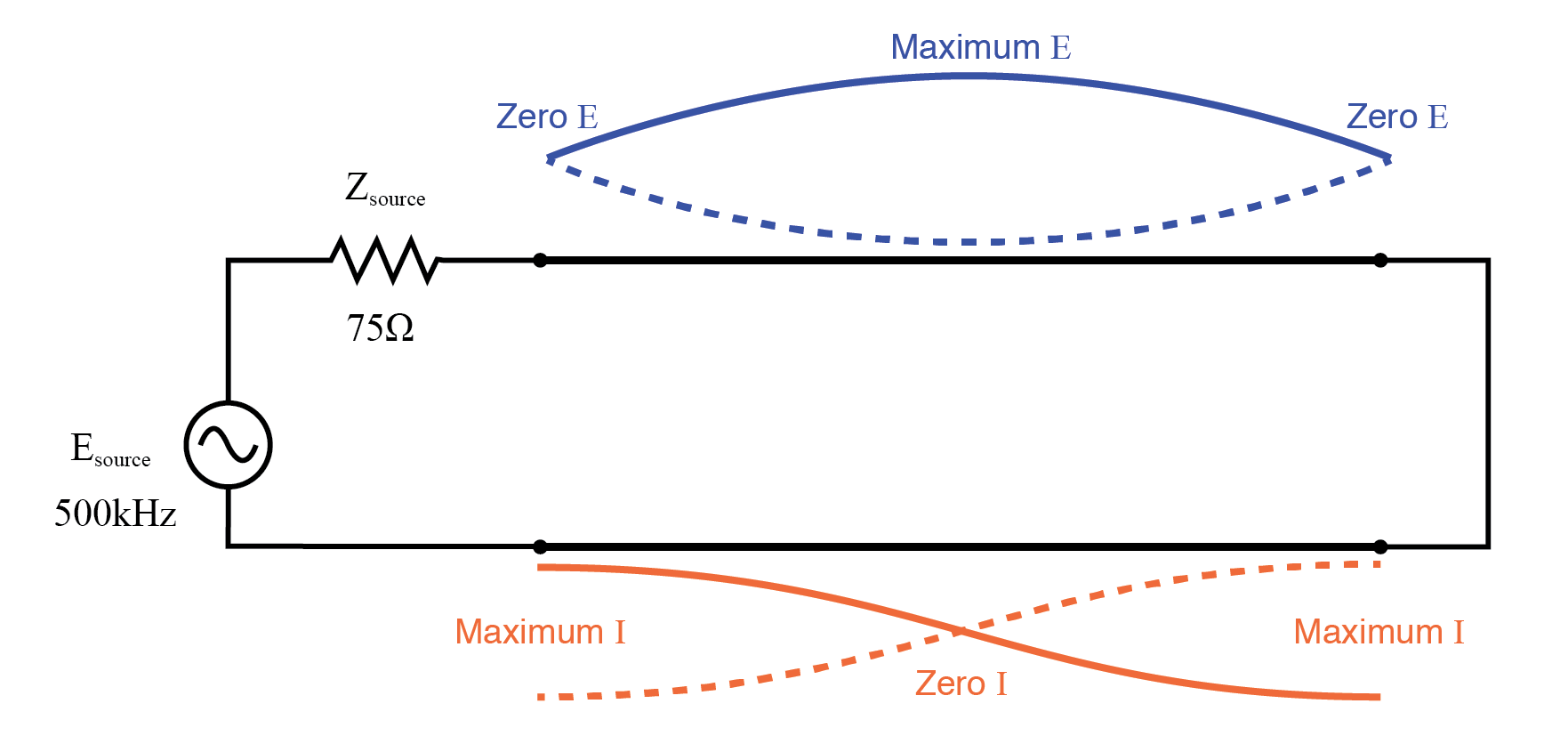
半波短路传输线上的全波驻波模式。

3/4 波短路传输线上的 1 1/2 驻波模式。

全波短路传输线上的双驻波。

在这两个电路示例（开路线路和短路线路）中，能量反射是全部：到达线路末端的入射波 100% 被反射回源。

但是，如果传输线终止于开路或短路以外的某种阻抗，反射将不那么强烈，沿线的电压和电流的最小值和最大值之间的差异也是如此。

假设我们要用 100 Ω 电阻器而不是 75 Ω 电阻器来终止我们的示例线路。 （下图）检查相应的 SPICE 分析的结果，以了解阻抗失配在不同源频率下的影响：（下图）

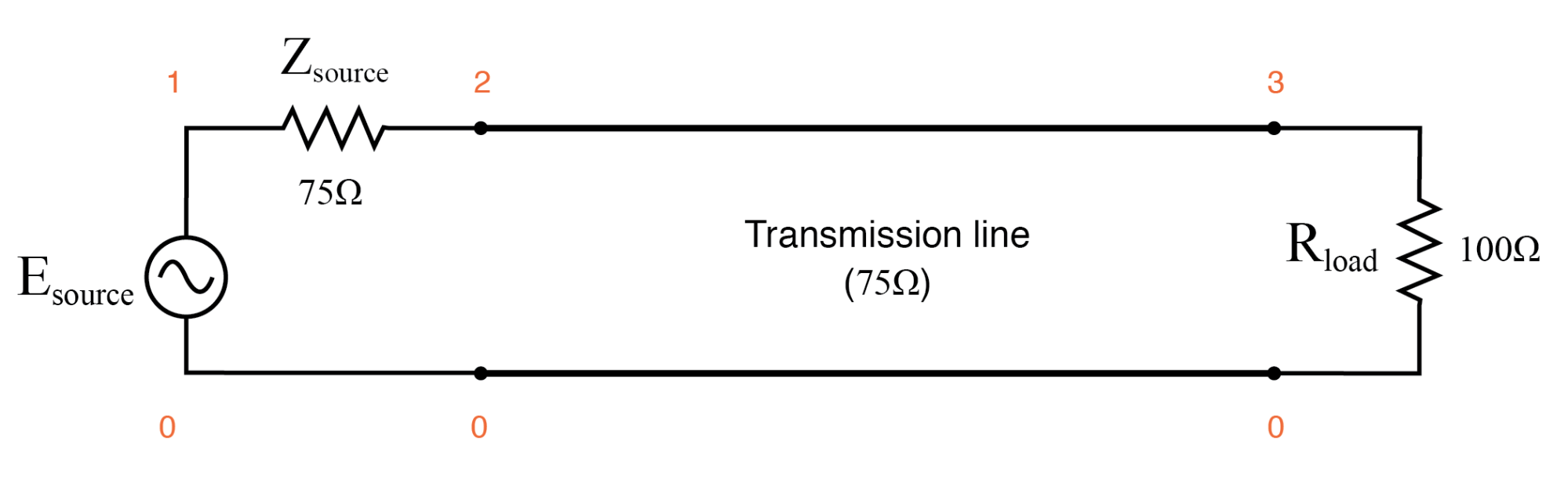
传输线因不匹配而终止

传输线 v1 1 0 交流 1 罪 资源 1 2 75 t1 2 0 3 0 z0=75 td=1u 加载 3 0 100 .ac lin 101 1m 1meg * 使用“Nutmeg”程序进行绘图分析 。结尾 

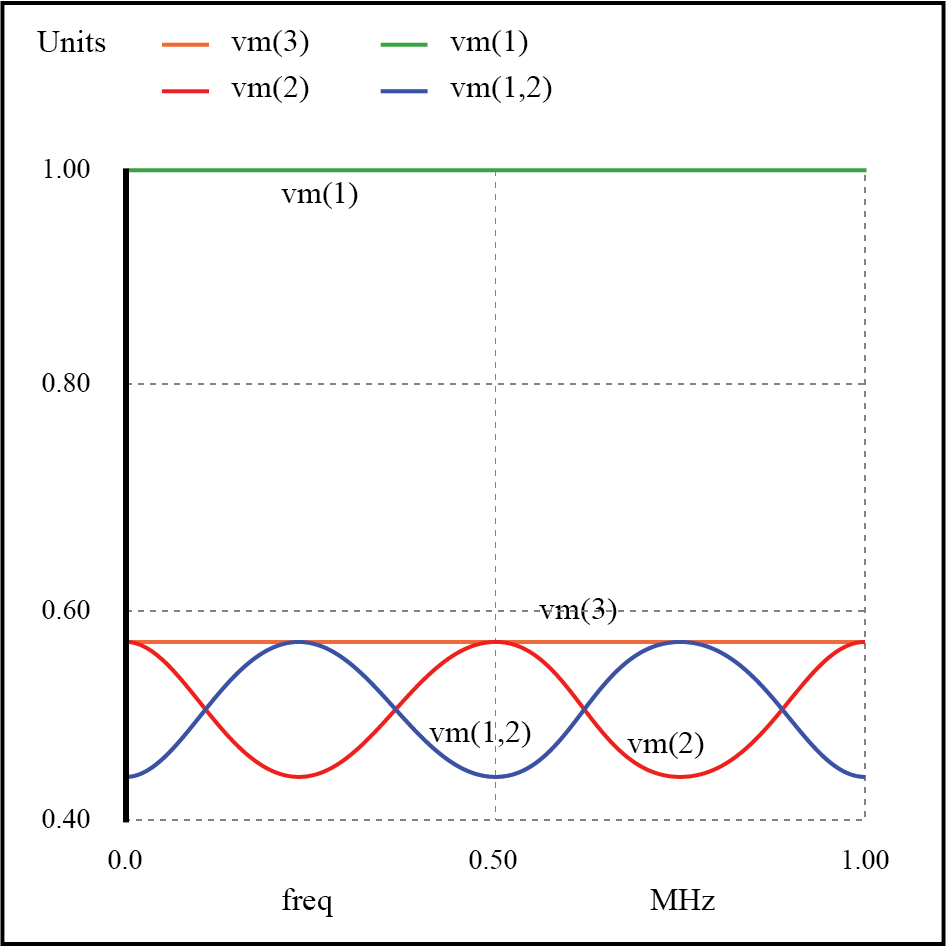
不匹配传输线上的弱共振

如果我们运行另一个 SPICE 分析，这次打印数值结果而不是绘制它们，我们可以准确地发现在所有有趣的频率上发生了什么：

传输线 v1 1 0 交流 1 罪 资源 1 2 75 t1 2 0 3 0 z0=75 td=1u 加载 3 0 100 .ac 林 5 1m 1meg .print ac v(1,2) v(1) v(2) v(3) 。结尾 

频率 v(1,2) v(1) v(2) v(3) 1.000E-03 4.286E-01 1.000E+00 5.714E-01 5.714E-01 2.500E+05 5.714E-01 1.000E+00 4.286E-01 5.714E-01 5.000E+05 4.286E-01 1.000E+00 5.714E-01 5.714E-01 7.500E+05 5.714E-01 1.000E+00 4.286E-01 5.714E-01 1.000E+06 4.286E-01 1.000E+00 5.714E-01 5.714E-01 

在所有频率下，源电压 v(1) , 应保持稳定在 1 伏。负载电压，v(3) , 也保持稳定，但电压较低：0.5714 伏。然而，线路输入电压 (v(2) ) 和源的 75 Ω 阻抗上的电压降 (v(1,2) ，表示从电源汲取的电流）随频率变化。

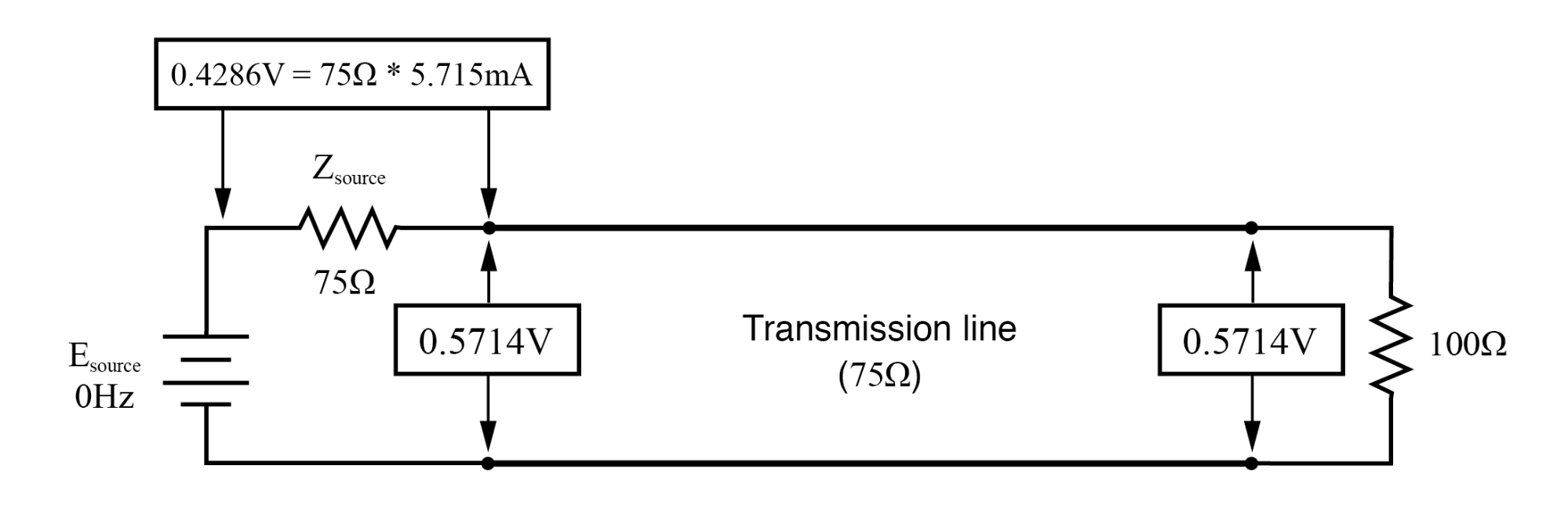
在 f=0 Hz 时：输入：V=0.57.1​​4，I=5.715 mA；结束：V=0.5714，I=5.715 mA。

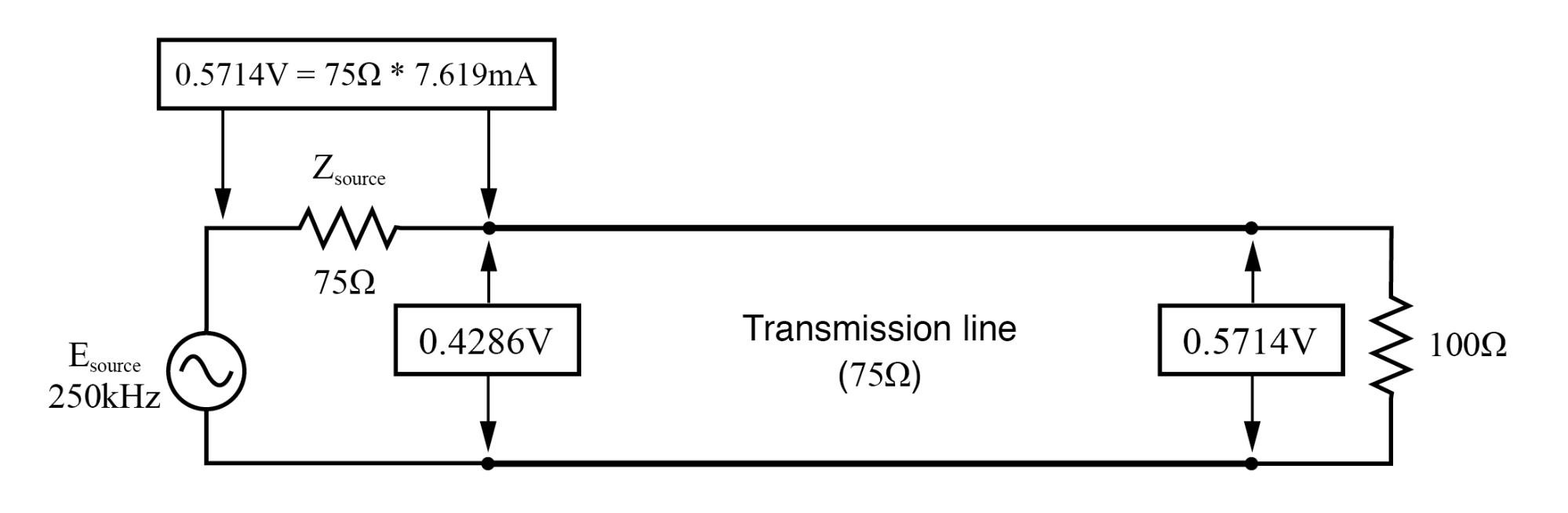
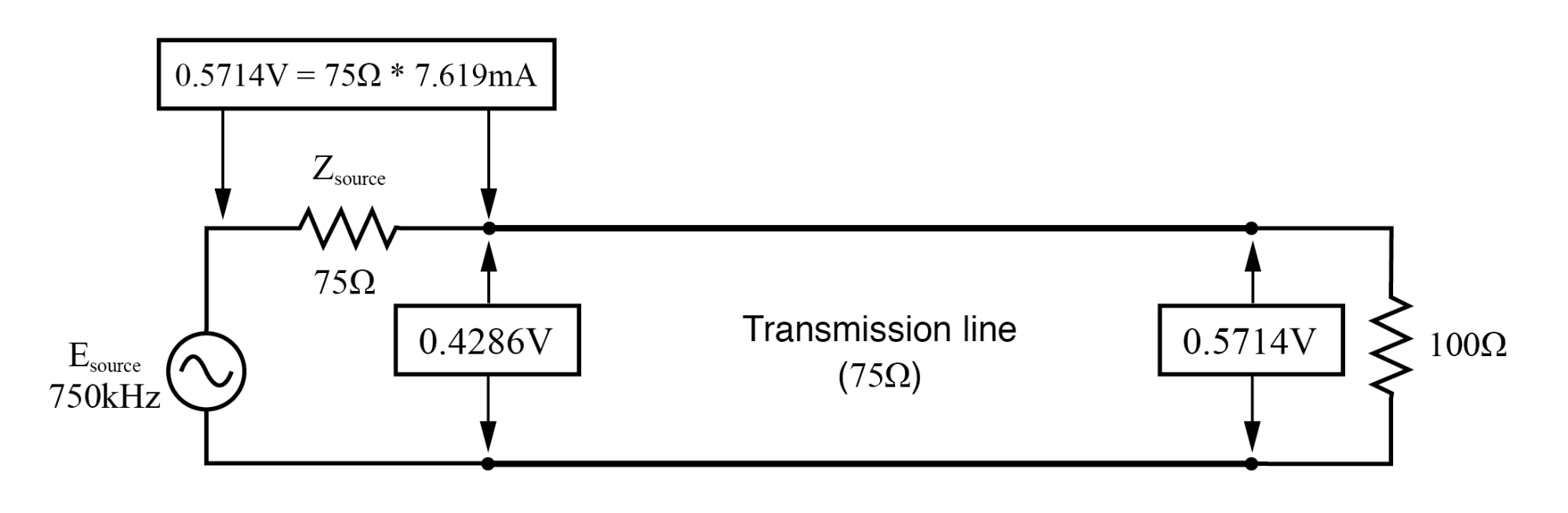
在 f=250 KHz：输入：V=0.4286，I=7.619 mA；结束：V=0.5714，I=7.619 mA。

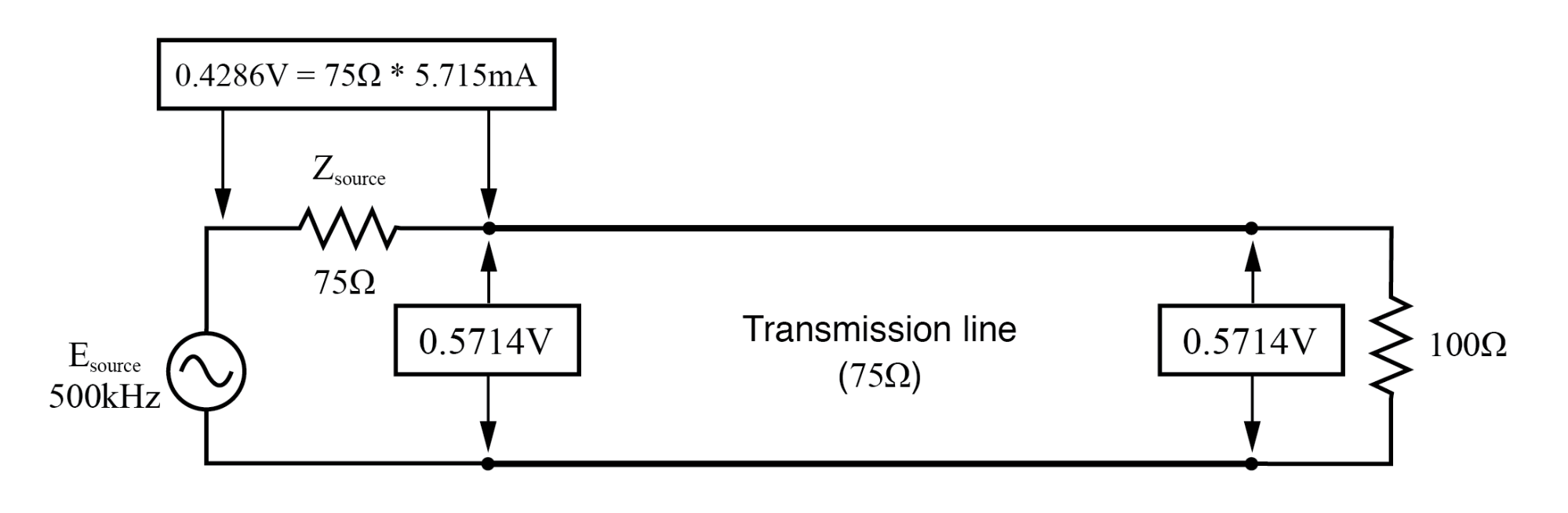
在 f=500 KHz 时：输入：V=0.5714，I=5.715 mA；结束：V=5.714，I=5.715 mA。

在 f=750 KHz 时：输入：V=0.4286，I=7.619 mA；结束：V=0.5714，I=7.619 mA。

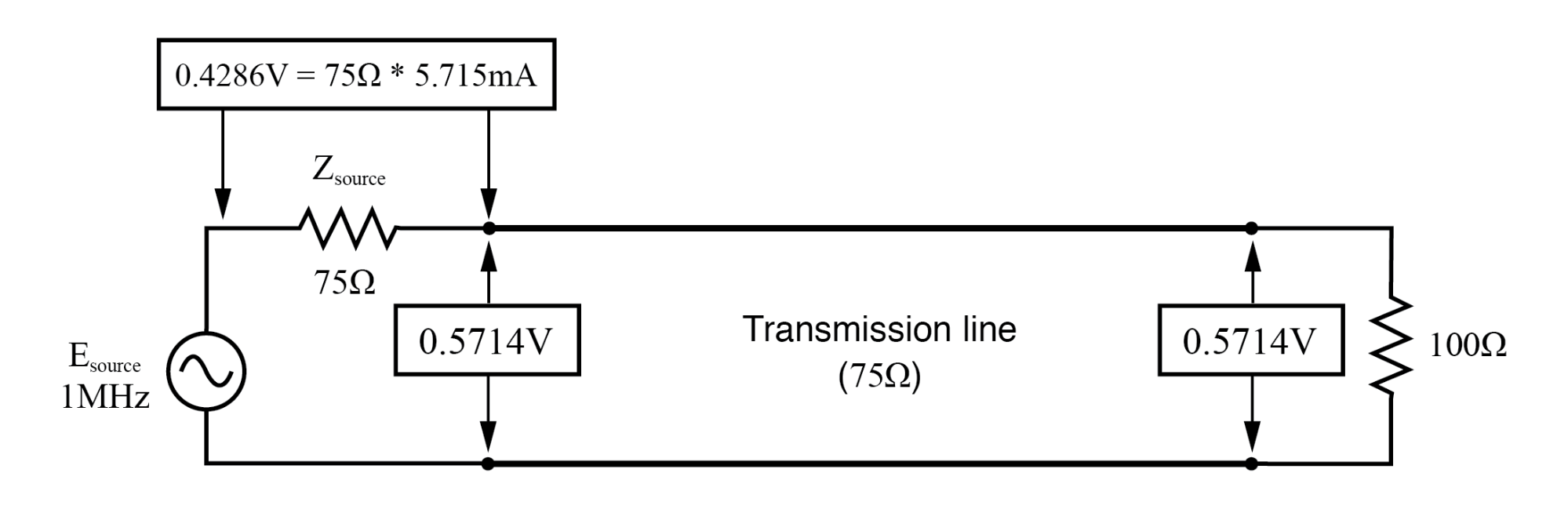
在 f=1 MHz 时：输入：V=0.5714，I=5.715 mA；结束：V=0.5714，I=0.5715 mA。

在基频的奇次谐波处（250 kHz，上图 3 和 750 kHz，上图），我们看到传输线每一端的电压电平不同，因为在这些频率下，驻波终止于节点的一端另一端在波腹。

与开路和短路传输线示例不同，这条传输线上的最大和最小电压电平没有达到 0% 和 100% 源电压的相同极值，但我们仍然有“最小值”和“最大”电压。

（上图 6） 电流也是如此：如果线路的终端阻抗与线路的特征阻抗不匹配，我们将在线路上的某些固定位置有最小和最大电流点，对应于驻流波的节点和波腹。

驻波比

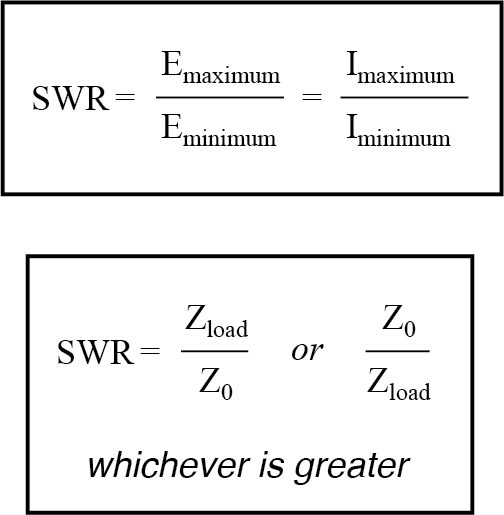
表示驻波严重程度的一种方法是电压或电流的最大振幅（波腹）与最小振幅（节点）的比率。

当线路因开路或短路而终止时，此驻波比 , 或 SWR 被赋值为无穷大，因为最小振幅将为零，任何有限值除以零都会导致无穷大（实际上，“未定义”）商。

在本例中，75 Ω 线路端接 100 Ω 阻抗，SWR 将是有限的：1.333，计算方法为 250 kHz 或 750 kHz（0.5714 伏）下的最大线路电压并除以最小线路电压（ 0.4286 伏）。

驻波比也可以通过取线路的终端阻抗和线路的特性阻抗，并将这两个值中的较大值除以较小值来计算。在本例中，100 Ω 的终端阻抗除以 75 Ω 的特征阻抗得到的商正好是 1.333，与之前的计算非常接近。

一条完美端接的传输线的 SWR 为 1，因为沿线长度的任何位置的电压都是相同的，电流也是如此。

同样，这通常被认为是理想的，不仅因为反射波构成未传递给负载的能量，而且因为驻波波腹产生的高电压和电流值可能会使传输线的绝缘（高压）和导体（大电流）。

此外，具有高 SWR 的传输线往往充当天线，将电磁能从传输线上辐射出去，而不是将其全部引导至负载。这通常是不可取的，因为辐射能量可能会与附近的导体“耦合”，从而产生信号干扰。

关于这一点的一个有趣的脚注是天线结构——通常类似于开路或短路的传输线——通常设计为在高 驻波比，正是为了最大化信号辐射和接收。

下图（下图）显示了无线电发射系统中连接点的一组传输线。两端带陶瓷绝缘帽的大铜管是50Ω特性阻抗的刚性同轴传输线。

这些线路将射频功率从无线电发射器电路传送到位于天线结构底部的小型木制掩体，然后从该掩体传送到具有其他天线结构的其他掩体：

连接刚性线路的柔性同轴电缆。

连接到刚性线路（同样具有 50 Ω 特性阻抗）的柔性同轴电缆将 RF 功率传导至防护罩内的电容和电感“定相”网络。将两条刚性管线连接在一起的白色塑料管将“填充”气体从一条密封管线输送到另一条密封管线。

这些线路是充气的，以避免在其中收集水分，这对于同轴线来说是一个明确的问题。请注意用作跳线的扁平铜“带”，用于将柔性同轴电缆的导体连接到刚性线路的导体。

为什么是扁平的铜带而不是圆线？由于趋肤效应，使得圆形导体的大部分横截面积在射频下无用。

像许多传输线一样，它们在低 SWR 条件下运行。但是，正如我们将在下一节中看到的，传输线中的驻波现象并不总是不受欢迎的，因为它可能被用来执行有用的功能：阻抗变换。

评论：

• 驻波 是不传播的电压和电流波（即它们是静止的），而是沿传输线的入射波和反射波之间干扰的结果。
• 一个节点 是最小值驻波上的一个点 幅度。
• 一个反节点 是最大值驻波上的一个点 幅度。
• 只有当终端阻抗与线路的特征阻抗不匹配时，驻波才能存在于传输线路中。在完美终止的线路中，没有反射波，因此根本没有驻波。
• 在某些频率下，驻波的节点和波腹将与传输线的末端相关，从而导致共振 .
• 传输线上的最低频率谐振点是传输线长度为四分之一波长的位置。谐振点存在于基波（四分之一波长）的每个谐波（整数倍）频率处。
• 驻波比 , 或 SWR , 是最大驻波幅度与最小驻波幅度之比。它也可以通过将终端阻抗除以特征阻抗来计算，反之亦然，得出最大商。没有驻波的线（完美匹配：Zload 到 Z0）的 SWR 等于 1。
• 传输线可能会被驻波的高最大振幅损坏。电压波腹可能会破坏导体之间的绝缘，电流波腹可能会使导体过热。