硼烯稳定性和STM图像的第一性原理研究

背景

自从发现石墨烯以来，二维 (2D) 材料因其独特的物理性质和在下一代电子和能量转换设备中的潜在应用而成为最活跃的纳米材料之一 [1,2,3,4,5, 6,7]。最近，一类二维硼纳米结构被发现并引起了极大的关注[8,9,10,11,12,13,14,15,16,17,18,19,20,21]。然而，直到最近，没有证据表明二维硼片可以通过实验实现，曼尼克斯等人。 [22] 和冯等人。 [23] 在实验实现原子薄二维硼片方面取得了惊人的进展。扩展后的二维硼片被称为“硼烯”，类似于石墨烯。

在过去的二十年中，已经发现了许多二维硼纳米结构 [8,9,10,11,12,13,14,15,16,17,18,19,20,21]。除了六边形片和三角形片[20, 21]，以及屈曲三角形片[8]，其他带有六边形孔的二维硼片，如α -sheet [9, 18], β -sheet [9, 18], γ -sheet [19] 和 g1/8 和 g2/15 sheet [15]，通过 ab initio 计算进行了检查。有人提出具有六边形空位的三角形平面硼晶格更稳定[9]。计算和实验研究组都报告了各种具有不同六边形孔图案的三角形硼层 [11, 13,14,15,16]。然而，所有这些单原子薄硼层的能量都高于硼的三维（3D）体态，这意味着硼的二维结​​构在热力学上处于劣势。因此，需要一个足够“粘性”的衬底来抑制 3D 成核​​势垒以吸引原子进入 2D 路线。

最近，通过第一性原理计算探索了金属和金属硼化物衬底上硼片的形成[24]；这表明硼片可以在 Ag(111) 和 Au(111) 表面上生长。此外，Piazza 等人的 [14] 研究提供了实验证据，证明基于他们对 B36 簇的观察，单层硼片是可以实现的；它被证明是一个高度稳定的平面簇，带有一个中心六边形孔 [14]。最近，两组[22, 23]通过分子束外延直接蒸发纯硼源，成功地在银表面合成了原子级薄结晶二维硼片。

曼尼克斯等人。 [22] 使用高分辨率扫描隧道显微镜 (STM) 表征在银基材上发现硼片的两个不同相：条纹相和均相。冯等人。 [23] 还发现了硼片的两相，它们看起来与 Mannix 等人的报告中报道的非常相似，他们将具有锯齿形突起行的均相描述为硼片的 χ3 晶格。另一方面，他们对条纹阶段的解释则大相径庭。曼尼克斯等人。 [22] 将条纹相指定为没有空位的屈曲三角形晶格。但冯等人。 [23] 提出条纹相为显示平行六边形孔行的矩形晶格，称为β12片。

这些二维硼片的确切配置和性能以及应用引起了极大的关注 [19, 22, 24, 25]。据报道，弯曲的三角形硼烯是一种高度各向异性的金属，沿扶手椅方向具有高杨氏模量，超过了石墨烯 [22]。孙等人。还发现屈曲三角形硼烯的晶格热导率具有很强的各向异性 [26]。此外，高等人。据报道，β12 硼烯和 χ3 硼烯可能是除 MgB2 薄膜之外的另一种硼超导相 [27]。然而，β12 硼烯和 χ3 硼烯的热力学稳定性是有争议的 [27, 28]。根据 Gao 等人的研究，β12 硼烯和 χ3 硼烯都是稳定的 [27]。但佩内夫等人。据报道，β12 硼烯和 χ3 硼烯在其声子谱中的 G 点附近都有虚频 [28]。

为了更好地理解实验上可实现的硼烯，我们通过第一性原理计算系统地研究了可能的原子结构及其稳定性，以及电子特性。我们的结果表明 β12 和 χ3 片层在热力学上是不稳定的。此外，屈曲三角形、β12 和 χ3 片的配置都显示出金属特征。此外，我们模拟了 Ag(111) 表面硼的独立和外延单层的 STM 图像；我们发现Ag(111)表面的屈曲三角形和β12硼片看起来都是条纹相，但几乎没有区别。

计算方法

计算是通过使用基于密度泛函理论 (DFT) [29, 30] 的 Vienna ab-initio 模拟包 (VASP) 进行的。投影仪增强波方法用于计算电子 - 离子相互作用 [31, 32]。并且使用 Perdew-Burke-Ernzerhof (PBE) 函数 [33] 通过广义梯度近似 (GGA) 描述电子交换-相关相互作用。波函数以平面波为基础展开，能量截止值为 500 eV。第一个 Brillion 区域分别用 25 × 15 × 1、15 × 9 × 1 和 11 × 11 × 1 k 网格对硼烯的屈曲三角形、β12 和 χ3 相进行采样。为了模拟 2D 硼片，沿 Z 方向包含至少 20 Å 的真空空间，以最大限度地减少周期性图像之间的相互作用。收敛标准设置为10 ⁻⁵ 自洽过程的两个离子步骤之间的 eV。所有结构都完全松弛，直到每个原子上的力小于 0.02 eV Å ^-1 ，底部两层银原子固定。声子色散谱已经通过使用在 PHONOPY 包中实现的有限位移方法计算出来 [34]。

STM 图像使用 Tersoff-Hamann 公式及其扩展 [35] 进行模拟。简而言之，假设尖端的状态密度是恒定的，我们可以用局部状态密度 \( \rho \left(\overrightarrow{r},E\right) \) 来近似 STM 隧道电流，作为只有具有以下表达式的变量：

其中 \( \rho \left(\overrightarrow{r},E\right) \) 是样品表面的 LDOS， \( {\psi}_i\left(\overrightarrow{r}\right) \) 是具有能量 E 的采样波函数 我 , 和 E F 是费米能量。当\( \rho \left(\overrightarrow{r},E\right) \) 中的状态被填满时，通常也引用\( \rho \left(\overrightarrow{r},E\right) \) 作为状态的电荷密度。基于计算的电子密度，使用恒流模式获得模拟的STM图像。

结果与讨论

图 1 显示了我们对硼烯的屈曲三角形、β12 和 χ3 晶格结构的计算结果。与石墨烯的单原子薄平面六边形构型不同，屈曲的三角形硼烯显示出沿一个晶格方向的屈曲。另一方面，β12 和 χ3 硼烯的结构是平面的，没有平面外屈曲。图 1a 显示在屈曲三角形硼烯的晶胞中有两个硼原子。并且屈曲三角形硼烯的空间群是Pmmn。我们优化的晶格常数是 a =1.613 Å 和 b =2.866 Å，与之前的理论和实验结果一致 [22]。图1b所示的β12硼烯沿锯齿形方向具有填充和空心六边形；对应的空间群是P2mm。晶胞中有五个硼原子。沿 a 的晶格常数为 2.916 和 5.075 Å 和 b 方向。 χ3 硼烯的晶胞是菱形的，具有四个硼原子，晶格常数为 4.448 Å。它的空间群是C2mm。表1列出了我们对晶格常数的计算结果，与之前的结果[22,23,27,36]非常吻合。

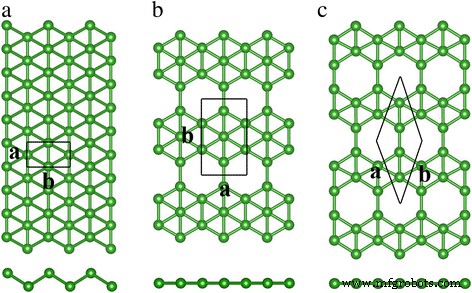
带扣三角形的顶视图和侧视图 (a ), β12 (b ) 和 χ3 (c ) 硼片。绿色球代表硼原子。由黑色实线包围的矩形和菱形表示单元格。字母 a 和 b 表示晶格参数

如图 1 所示，β12 和 χ3 片中都有空位，但在屈曲三角晶格中没有空位，并且 β12 和 χ3 硼烯中的空位数量不同。空位浓度η 定义为晶胞中空位数量与总位点（包括空位）的比值；它是从全局和局部角度描述硼片的数量[9]。 η 在 β12 晶格中为 1/6，在 χ3 晶格中为 1/5。与β12晶格相比，图1c显示χ3硼烯中相邻的空位行在Z字形方向上移动了晶格常数的一半，导致平面对称性为C2mm。

对于三种结构，我们使用以下方程计算每个硼原子的平均能量，并用它来比较三种结构的相对稳定性；该方法已应用于参考文献。 [23]

其中 E 硼烯和n 分别是一个晶胞中硼原子的能量和数量。我们的计算结果总结在表 2 中。这表明 β12 相最稳定，而 χ3 相最不稳定，相对较高的能量为 0.08 eV。

然后我们计算了屈曲三角形、β12 和 χ3 硼烯三相的声子色散谱。图 2 显示了沿高对称方向的声子色散谱。如图 2a 所示，弯曲的三角形硼烯有三个声子分支和三个光学声子分支。它还显示了沿 X-G 方向的 G 点附近的虚数值，表明晶格沿 a 不稳定 方向，这解释了沿 a 形成的条纹 实验 STM 图像中的方向 [23]。事实上，最近的研究表明，即使在 0.08% 的拉伸应力下，双轴拉伸和单轴拉伸也不能稳定独立的屈曲三角形硼烯 [36, 37]。图 2b、c 表明在 β12 和 χ3 相的 G 点附近也存在虚频率。结果表明，屈曲三角形、β12和χ3三相均不稳定。

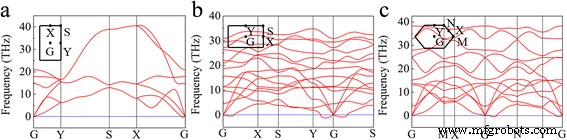
a的声子色散 带扣三角形，b β12 和 c χ3 硼片。高对称点显示在左上角

我们进一步研究了屈曲三角硼烯、β12 硼烯和 χ3 硼烯的电子结构。计算出的沿高对称方向的能带结构如图 3 所示。如图 3 所示，屈曲三角形、β12 和 χ3 硼烯三相均为金属相。特别是，对于如图 3a 所示的屈曲三角形硼烯，三个能带穿过费米能级：一个沿 S-Y 方向，另外两个沿 G-X 方向。然而，我们在上面的章节中已经提到，屈曲三角形是沿着 b 方向，分别沿 X-S 和 Y-G 方向打开 9.63 和 4.32 eV 的带隙。这表明屈曲的三角形硼烯表现为具有强各向异性的金属，其导电性被限制在无波纹的a 方向。

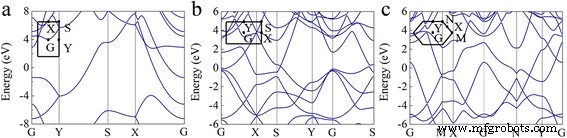
a 的计算能带结构 带扣三角形，b β12 和 c χ3 硼片。费米能量设置为零。高对称点显示在左上角

此外，我们研究了 Ag(111) 衬底上的屈曲三角形、β12 和 χ3 硼片的原子结构和稳定性。结果如图 4 所示。 Ag(111) 表面的屈曲三角硼烯的晶胞是独立屈曲三角硼烯的 (1×3) 超胞和 Ag 的矩形 1×(√3)R30° 超胞(111) 基材。对于Ag(111)表面β12片层的构型，晶胞是β12硼烯的晶胞和Ag(111)表面的1×(√3)R30°超晶胞。我们的计算表明，β12 硼烯与 Ag(111) 表面的匹配（~ 1% 错配）比弯曲的三角形硼烯（~ 3% 错配）更好。 χ3 硼烯在 Ag(111) 表面形成两种构型，如图 4c、d 所示，分别命名为 χ3 和 χ3'。 χ3的晶胞为菱形，晶格常数为a =8.67 Å，且 χ3' 的晶胞是正交晶胞，晶格参数为 a =2.89 Å 和 b =25.02 Å；它是Ag(111)表面的1×(5√3)R30°超胞。

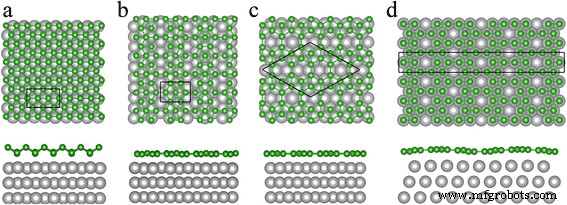
Ag(111) 表面硼片的顶视图和侧视图。 一 带扣三角形，b β12，c χ3 和 d χ3' 硼片。绿色和灰色球分别代表硼和银原子。黑色实线包围的矩形和菱形表示Ag(111)表面硼片的晶胞

根据我们的计算，从 Ag(111) 表面到屈曲三角形硼烯的上下硼原子层的垂直距离分别为 2.5 和 3.3 Å，表明硼片与银基板之间的相互作用较弱。 β12、χ3 和 χ3' 片在 Ag(111) 表面上均保持平面，硼片与 Ag 表面之间的垂直距离为 2.4~2.9 Å。结果与 Mannix 等人报道的 ~ 2.7 至 3.1 Å 的测量厚度一致。 [22]。我们将 Ag 衬底上硼烯的屈曲三角形、β12、χ3 和 χ3' 相的原子结构与独立式硼烯的对应物进行了比较，发现这四种结构变化很小。屈曲高度h 屈曲三角形硼烯的长度从 0.910 到 0.857 Å 较短，而 B-B 长度较长，约为 0.1 Å。此外，β12硼烯中的六边形空位沿一个方向收缩，而χ3硼烯中的六边形空位略大。

与独立式硼烯相对稳定性的计算类似，我们通过以下公式进一步计算了Ag（111）表面硼片的每个硼原子的平均能量：

其中 E tot 是硼片和 Ag(111) 表面的总能量，E sub 是 Ag 衬底的能量，n 是一个晶胞中硼原子的数量。我们的结果表明，基于它们的相近能量，在 Ag(111) 表面形成屈曲三角形、β12、χ3 和 χ3' 晶格的可能性是相似的。此外，相对于独立片，Ag(111) 表面上硼烯的能量每个硼原子低 0.1~0.2 eV。这意味着Ag(111)表面稳定了硼烯。

图 5 显示了我们模拟的 Ag(111) 表面上独立和生长的硼片的 STM 图像，以及独立硼片的部分电荷密度。如图 5a 所示，独立式带扣三角形硼板具有亮点条纹。图 5d 表明亮点来自上部硼原子的 pz 轨道。图 5b 显示了被明亮六边形包围的一排黑色圆形斑点。显然，图 1b 所示的 β12 晶格中的六边形空位导致暗点，而亮六边形对应于 σ 如图 5e 所示，六边形孔周围硼原子的轨道。如图 5c 所示，χ3 片显示哑铃形亮点的菱形图案。这些明亮的哑铃点实际上是两个硼原子的 pz 轨道和 σ 它们之间形成轨道。

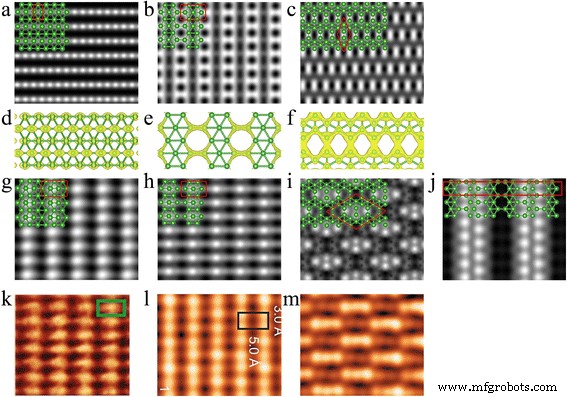
Ag(111) 表面上独立式和外延硼片的模拟 STM 图像。独立式a 三角形，b β12 和 c χ3 硼片。独立式 d 的部分电荷密度 三角形，e β12 和 f χ3 硼片。 g 带扣三角形，h β12，i χ3 和 j Ag（111）表面上的χ3'硼片。偏置电压为 1.0 V。绿色球代表硼原子。由红色实线包围的矩形和菱形分别表示 Ag(111) 表面上独立和生长的硼片的晶胞。实验观察到的 k 参考文献中的条纹阶段。 [22], l 参考文献中的条纹阶段。 [23] 和 m 参考文献中的均相[23]

由于硼烯和Ag（111）表面的晶胞之间的不匹配，Ag基板上的硼片相对于独立的具有更大的单元图案。图 5g 显示了我们在 Ag(111) 表面上弯曲的三角形硼片的模拟 STM 图像。它显示纺锤形亮点条纹，与实验观察结果非常吻合 [22]。与图 5a 所示的独立屈曲三角形硼片的图像相比，Ag（111）表面上的屈曲三角形硼片的 STM 图像的晶胞增加了三倍。形状由圆形变为纺锤形。图 5h 所示的 Ag(111) 表面 β12 片层的 STM 图像显示了成排的椭圆形暗点，其四个角上有四个亮点围绕。与图 5b 所示的独立 β12 片的图像不同，亮点来自六边形中心硼原子的 pz 轨道。如图 5i 所示，χ3 片具有菱面体 STM 图案，与实验观察到的 S2 相非常吻合 [23]。菱面体晶胞中的一组亮点对应于σ 晶胞中较高硼原子的轨道和pz轨道，而其他硼原子由于较低而看不见。

曼尼克斯等人。 [22] 和冯等人。 [23] 都根据他们的 STM 观察报告了 Ag(111) 表面上二维硼片的条纹相，并且两个 STM 图像都具有平行的突起行。但是，两次实验观测中亮点的形状不同；它们在 Mannix 等人的报告中是纺锤形 [22]，在 Feng 等人的 [23] 中是椭圆形。我们的屈曲三角形和 β12 硼片的模拟 STM 图像与参考文献中实验观察到的条纹相非常匹配。 [22] 和参考文献。 [23] 和图 5g 中显示的图像，h 清楚地再现了 Mannix 等人的实验观察结果之间的差异。 [22] 和冯等人。 [23]。它还为我们提供了一种区分屈曲三角形和β12两种晶格的方法。至于 Ag(111) 表面 χ3 片的 STM 图像，如图 5i 所示，它与实验观察 [23] 一致，但我们的结果表明亮点来自于边缘的硼原子。六边形空位而不是参考文献中所示的填充三角形区域。 [23].

为了进一步区分Ag（111）表面硼片的晶格结构，我们模拟了几种不同偏置电压下Ag（111）上硼片的STM图像。如图 6 所示，弯曲三角形硼烯的模拟 STM 图像在正电压下显示出纺锤形亮点条纹。但是在- 0.4 V的负偏置电压下，模拟的STM图像显示出明暗条纹，与实验结果[22]匹配良好。另一方面，β12 硼烯的模拟 STM 图像在正偏压和负偏压下均保持椭圆形。因此，屈曲三角形结构更可能是条纹相的正确配置。对于 χ3 硼烯的 STM 图像，图 6 表明所有图像中的亮点来自六边形空位边缘的硼原子，但它们的明亮对比度随着电压从正变为负而变化。当偏置电压为 0.2 和 - 0.4 V 时，斑点的亮度相似。此外，我们针对 χ3' 配置的模拟 STM 图像在 0.8 至 - 1.0 V 的偏置电压下看起来相似（图 6）。它们都显示出来自六方空位边缘硼原子的亮点，但只有较高的硼原子可见，晶胞中间的较低硼原子不可见。

Ag(111) 上硼片的模拟 STM 图像。 Ag(111) 上 a 处的带扣三角形硼烯 0.8，e 0.2, i − 0.4，m − 1.0 V. β12 硼烯在 Ag(111) 上 b 0.8，f 0.2, j − 0.4 和 n − 1.0 V. χ3 硼烯在 Ag(111) 上 c 0.8, g 0.2, k − 0.4 和 o − 1.0 V. χ3' 硼烯在 Ag(111) 上 d 0.8, h 0.2, l − 0.4 和 p − 1.0 V。绿色球代表硼原子。红色实线包围的矩形和菱形表示Ag(111)表面上生长的硼片的晶胞

结论

总之，我们对最近在金属表面生长的三个二维硼片（即屈曲三角形、β12 和 χ3 晶格）的原子结构、稳定性和电子性质进行了第一性原理计算。我们的计算表明，没有金属基材的支持，所有三个硼片都是热力学不稳定的。能带结构表明，弯曲的三角形硼片表现为具有强各向异性的金属，β12 和 χ3 硼片也是金属，没有能隙。此外，我们的结果表明，三种晶格的能量非常接近，屈曲三角形和 β12 硼片与 Ag(111) 表面之间的晶格匹配非常小。此外，我们发现Ag（111）上的弯曲三角形和β12硼片都形成了STM图像的矩形晶格和平行条纹图案，但几乎没有区别。我们的结果提供了区分两个晶格的详细信息。最重要的是，我们模拟的STM图像为实验观察到的Ag(111)表面的硼片提供了新的解释。

缩写

二维：

二维

3D：

三维

STM：

扫描隧道显微镜