通过退化特性的数值分析提高超表面偏振器的高性能

背景

纳米级光的控制已在纳米光学和纳米光子学中得到广泛研究。因此，迄今为止已经提出了不同类型的光子纳米结构。例如，具有超高品质 (Q) 因子的光子晶体 (PhC) 纳米腔 [1] 可以将光限制在亚波长区域。与 PhC 腔类似，高 Q 因子是通过微盘 [2, 3]、球形 [4] 和环形 [5] 腔实现的。那些具有高 Q 因子的腔体通常由透明介电材料组成。与那些介电腔相比，金属腔具有较低的 Q 因子，但可以减小其整个腔的尺寸。特别是，等离子体亚波长腔对于在极小尺度上控制光很重要[6]。尽管等离子体腔具有低 Q 因子，但它们可以将光压缩到深亚波长区域 [7]。这种极其有限的光有望成为融合光子学和电子学的关键[8]。

除了上述光子纳米结构之外，超表面最近在设计高功能和超薄光学器件方面引起了相当大的关注。有多种类型的超表面可以控制折射 [9]、反射 [10]、光致发光 [11]、荧光 [12-14]、波片 [15] 和分束器 [16]。偏振态是光的基本和重要特性之一，可以由超表面控制 [17-22]。数值和实验研究表明，具有堆叠互补结构的超表面偏振器在近红外区域具有 10,000 量级的高消光比 [23-26]。由于巴比涅原理，互补结构在几乎相同的波长处具有共振 [27, 28]。当互补结构处于共振状态时，对特定偏振表现出高透射率，而另一个结构处于非共振状态，对相同偏振表现出低反射率。结果，整个结构表现出高透射率。对于正交极化，电场和磁场交换的作用，导致高反射率。因此，具有互补结构的超表面表现出高消光比。然而，这种高性能的稳定性和可靠性令人深感担忧，因为超表面包含银，银会在大气中降解。为了避免这个问题，另一种方法是使用金作为等离子体材料，但由于金属损耗增加，这会降低偏振器的性能。因此，在实际应用中，超表面偏振器的稳定性和可靠性应该得到解决。

在这项研究中，我们研究了超表面偏振器的降解特性。我们表明偏振器的消光比表现出时间退化。作为退化的根源，我们关注表面形态对偏光片高性能的影响。为了描述形态，我们引入了两个模型。一种通过具有高斯白噪声的周期性曲线来描述表面粗糙度，而另一种则通过使用随机分布的纳米颗粒来描述粗糙度。我们还研究了金属损耗对高性能的影响。通过这些数值计算，我们揭示了导致退化的关键因素，并提出了一种具有高消光比的优化超表面偏振器。

方法/实验

高消光比测量的实验装置如图 1 所示。我们使用由三倍频 Nd:YAG（钇铁石榴石）激光器（Optolette 355，Opotek）泵浦的光学参量振荡器（OPO）作为光来源。脉冲宽度和重复频率分别为 7 ns 和 20 Hz。来自 OPO 的闲散光通过透镜聚焦在样品上，并通过格兰激光棱镜 (GLP) 线性偏振。传输的闲散光由扩展 InGaAs 光电探测器 (Edmund Optics) 测量。在该光学系统中，单个脉冲的光强波动会导致信噪比 (S/N) 较差。因此，为了消除这种波动的影响，我们测量了单个脉冲的平均透射率。为了监测单个脉冲的光强度，我们在镜头和 GLP 之间插入了一对光束采样器。一部分闲散光在第二个光束采样器 (BS2) 处反射，然后在反射中性密度 (ND) 滤光器处再次反射，该滤光器调整反射的激光强度，以免损坏光电探测器。调谐激光通过针孔入射到扩展的 InGaAs 光电探测器（Edmund Optics）上，该针孔阻挡了在 BS2 背面反射的不必要的“鬼”光（参见图 1 的插图）。第一光束采样器作为光路偏差的补偿器。

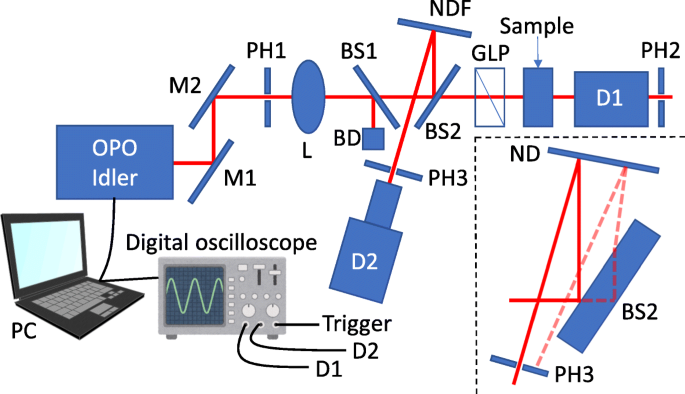
消光比测量的实验装置示意图。 M镜、PH针孔、L透镜、BS光束采样器、BD光束阻尼器、NDF中密度滤光片、GLP格兰激光棱镜、D探测器

使用此设置，我们如下评估消光比。发射信号计算为D 1=(1-R BS2)T GLPT 样本I ，其中 R BS2，T 普洛斯，T 样本和我 分别为 BS2 的反射率、GLP 的透射率、样品的透射率和 BS2 前方的光强。检测器2的信号强度计算为D 2=R BS2R NDFI ，其中 R NDF 是反射 ND 滤光片的反射率。请注意，光强度已充分降低，以便检测到的信号与光强度成正比。使用 D 1 和 D 2、我们可以计算T 样本为

评估 T 样品，我们还需要测量光学元件的反射率和透射率，比如光束采样器。这是不必要的，因为我们关注的是消光比，即透射率。通过将样品旋转 90°并以相同的设置测量透射率，我们可以简单地获得消光比 η 作为

其中上标 H 和 L 分别表示具有高透射率和低透射率的偏振态。在本文中，我们测量了 D 的比率 1/D 2对于正交偏振态并评估消光比η .

为了确认测量数据的有效性，我们基于严格耦合波分析 (RCWA) 结合散射矩阵方法 [29, 30] 和逆傅立叶方法 [31] 进行了数值计算。 Ag 和二氧化硅的介电常数分别从 [32] 和 [33] 获得。计算中使用的倒易格向量数为2601。

为了计算粗糙金属结构的透射率，我们使用了基于有限元方法的 COMSOL Multiphysics 商业软件。在之前的研究 [34] 中，粗糙度对光学响应的​​影响是通过金属介电常数虚部的增加来描述的。在本文中，除了金属损耗的增加外，我们还考虑了结构变化以及粗糙度对透射率的直接影响。我们分别处理了这两种影响。当仅考虑结构变化的影响时，我们将体介电常数应用于具有粗糙度的金属结构。另一方面，当仅考虑损耗增加的影响时，我们将修改后的介电常数应用于没有粗糙度的金属结构。我们将数值计算的相对容差设置为小于1%。

结果与讨论

图 2a 描绘了三层超表面偏振器的示意图。第一层具有与第三层互补的结构（见图 2b），两层均包含银 (Ag)。第二层和基材包含二氧化硅(SiO2)。如图 1c 所示，超表面具有矩形孔阵列（150 nm × 540 nm）对，并且在 x 中的周期为 900 nm 和 y 方向。金属层和介电层的厚度分别为 45 和 200 nm（见图 2d）。该样品是通过纳米压印光刻结合随后的干蚀刻技术制备的 [35]。 [26] 中描述了样品制备的细节。图3为制备样品的扫描电子显微镜（SEM）图像。

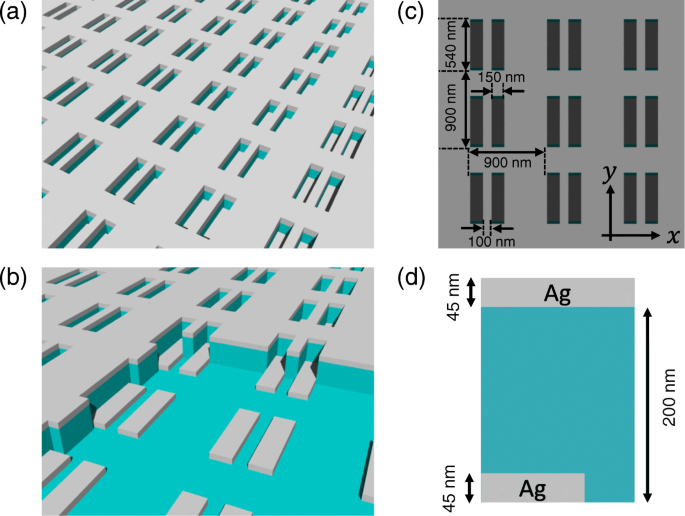
超表面偏振器的示意图（a ) 包含三层 (b ）。超表面在 x 中有一个周期为 900 nm 的矩形孔对阵列 和 y 方向 (c ）。金属层和介电层的厚度分别为 45 和 200 nm (d )

a 的 SEM 图像 超表面偏振器和 b 它的放大图像

我们使用分光光度计 (V-7200, JASCO, Japan) 来测量 x 样品的透射率 和 y 极化。图 4 显示了测量结果。蓝线和绿线表示 x 的透射率 和 y 极化，分别。对应于高透射率的蓝线是用高 S/N 比测量的。然而，对应于低透射率的绿线具有低信噪比，因此表明偏光片具有高消光比。特别是，绿线在波长超过 1350 nm 时具有负信号，因为透射光的强度低于分光光度计的噪声水平。因此，我们使用上一节中描述的光学系统来测量高消光比。

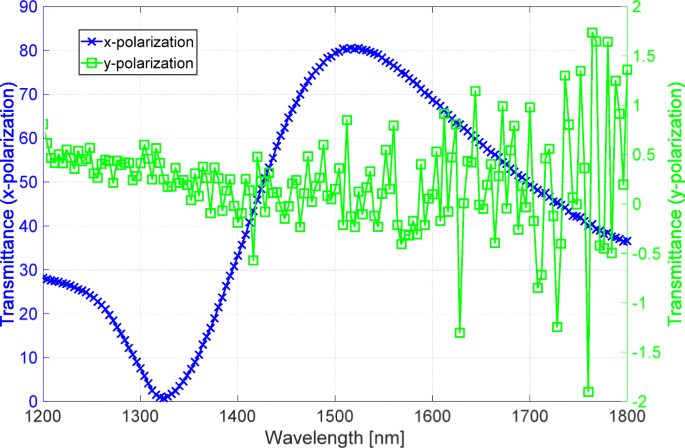
由分光光度计测量的透射光谱。蓝线和绿线是 x 的光谱 和 y 极化，分别

图 5a 显示了 x 的测量透射光谱 和 y 极化。对应于高透射率的蓝线具有与分光光度计测量的透射率相似的光谱曲线。对应于低透光率的绿线在 1625 nm 波长附近有明显的下降，这是分光光度计未测量到的。通过划分 x 的透射率 y 的极化 偏振，我们评估了图 5b 中所示的消光比光谱。消光比光谱在1640 nm波长附近峰值超过20,000。

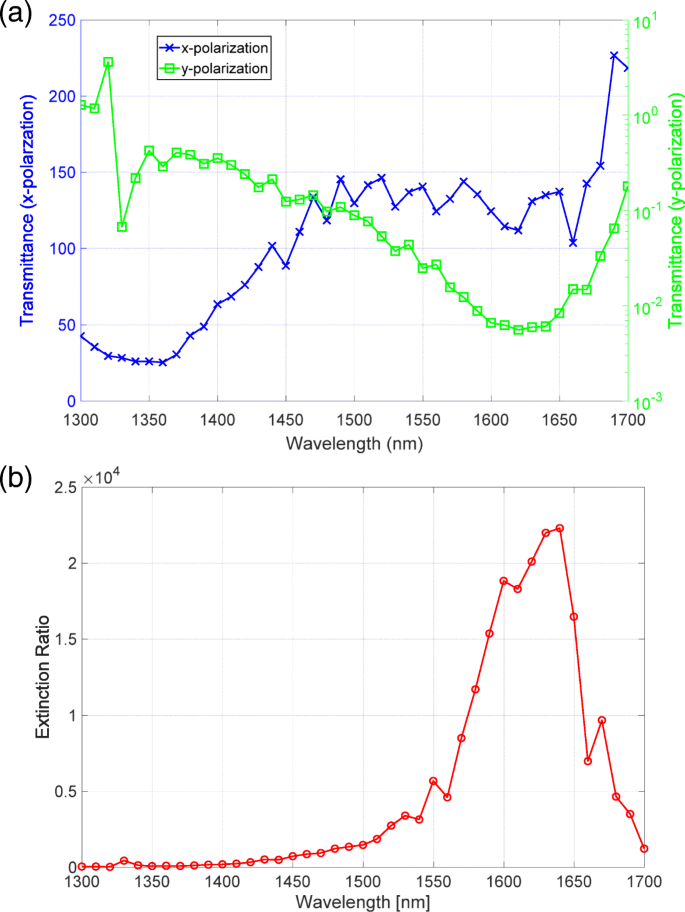
一 x 的透射光谱 （蓝色）和 y （绿色）偏振由图 1 所示的设置测量。b 超表面偏振器的消光比光谱

为考虑实测数据的有效性，我们将实测光谱与数值计算结果进行了比较。如图 6a 所示，高透射光谱与分光光度计测量的光谱一致。以对数刻度显示的低透射率光谱在 1640 nm 波长附近有明显的下降。该特征与观察到的光谱中的特征非常吻合。图6b所示的消光比谱峰为15000，与观测值接近。因此，测得的透射率和消光比光谱与数值计算结果一致，表明我们成功观测到超过20,000的高消光比。

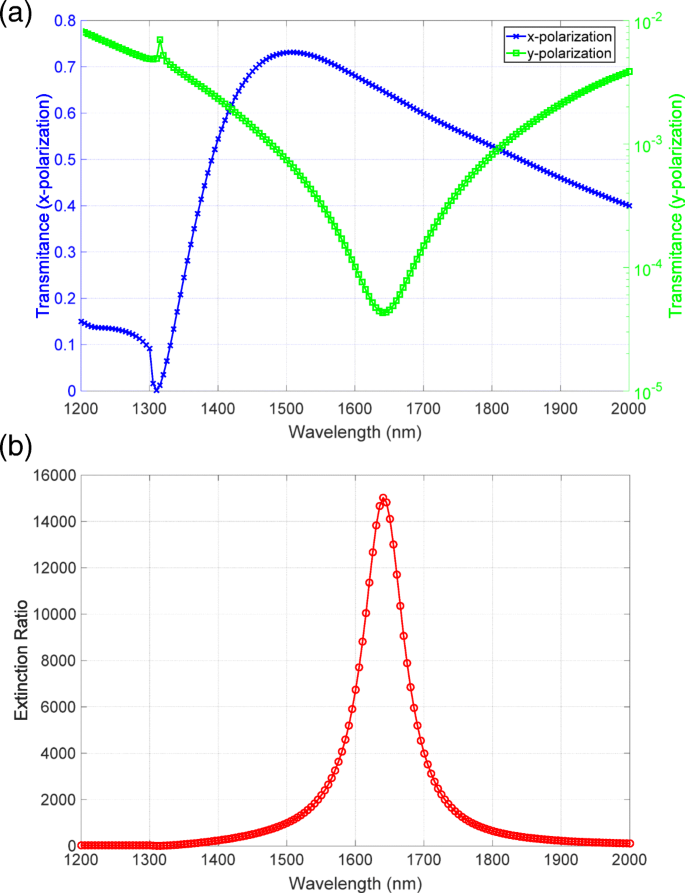
a的数值计算结果 透射率和b 消光比光谱。 a 中的蓝线和绿线 对应于 x 和 y 极化，分别

在对具有高消光比的超表面进行实验证明之后，我们将重点放在对时间降解的稳定性上，因为超表面包含银，在大气中会发生降解。图 7 显示了消光比的时间退化。红色、绿色和蓝色线分别是金属沉积后 6、7 和 9 天后观察到的消光比光谱。红线峰值超过20,000。经过一天的红线测量，消光比有所下降，但仍然有一个超过 10,000 的峰值。然而，绿线测量两天后，消光比显着下降，峰值为500。蓝线的线宽变宽，表明这种下降会导致损耗的增加。因此，消光比急剧下降，性能下降一个数量级。我们还发现了降解后消光比光谱的蓝移峰。对涉及性能下降的关键因素进行了研究。

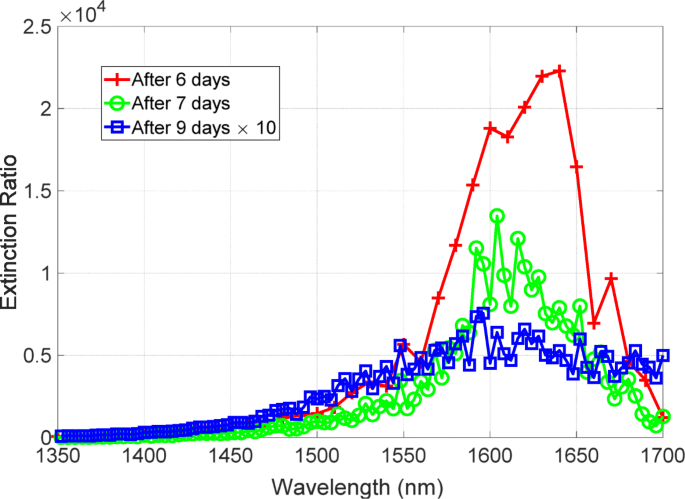
消光比的时间退化。红、绿、蓝线为金属沉积后6、7、9天的消光比谱

降解进行得很快，消光光谱的线宽变宽，表明这种降解过程会涉及一些结构变化。因此，我们研究了金属纳米结构的表面形态如何影响偏振器的性能。为了描述形态，我们引入了两个模型。一种用高斯白噪声的周期曲线描述表面，另一种用随机分布的纳米粒子描述表面。

首先，我们使用周期曲线研究模型。图 8a 描绘了建模表面。我们仅在底部金属层中引入粗糙度以节省 CPU 时间和内存资源。由于表面粗糙，金属层的有效厚度各不相同。因此，我们改变了图 8b 中绿色箭头指示的底层厚度。图 9a、b 分别显示了该结构的透射率和消光比光谱。即使存在粗糙度，超表面偏振器也具有 10,000 量级的高消光比，表明粗糙度不会显着降低性能。数值计算还显示了随着厚度的减小，消光比的红移光谱。这种红移由图 9a 中所示的透射率的光谱特征阐明。高透光率对金属厚度变化的灵敏度非常低，而低透光率则随着金属厚度的减小，倾角位置红移。消光比的峰值位置取决于低透射率的下降，导致红移。计算中出现的红移与实验观察到的蓝移特征不一致。

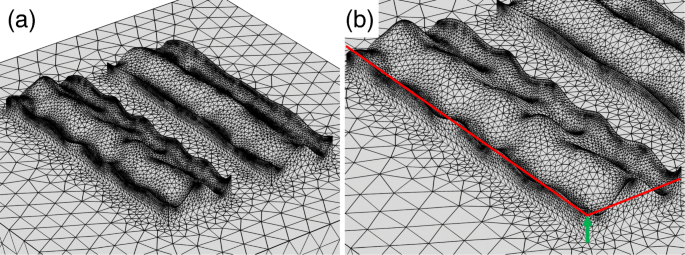
一 使用具有高斯白噪声的周期性曲线建模的粗糙表面。 b 绿色箭头表示的基础厚度在计算中是变化的

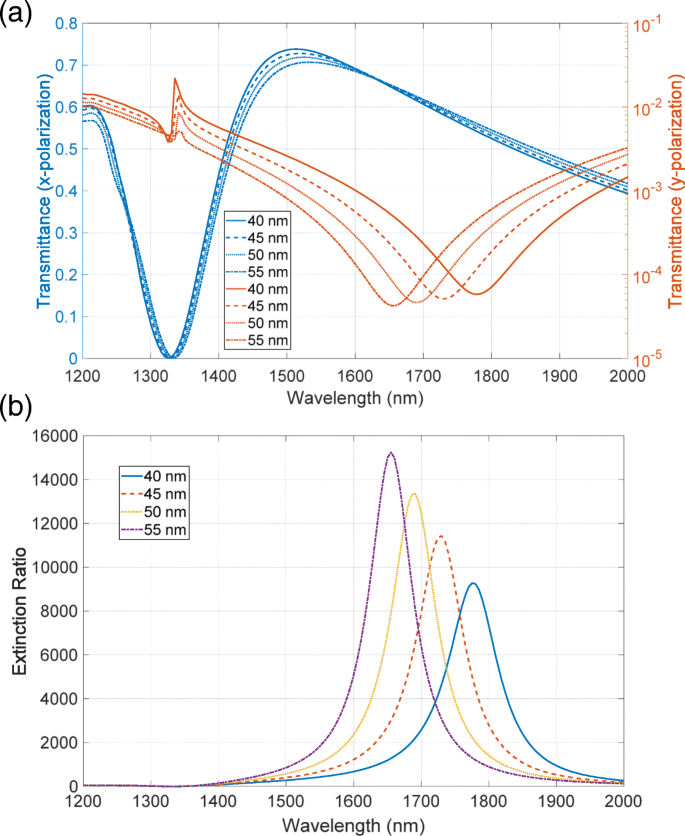
一 透射率和b 图 8 所示第一个模型的消光比光谱。底部金属层的基底厚度从 40 到 55 nm 以 5 nm 的步长变化

其次，我们通过纳米粒子研究模型。图 10a 描绘了建模表面，其中半径为 15、20 和 25 nm 的纳米粒子随机分布在底部金属结构的表面上，如图 10b 所示。我们按照均匀分布的随机数将半球状的纳米粒子放置在表面。在随机分布下，一些粒子有轻微的空间重叠，粒子之间的网格大小变得非常消耗内存。在这种情况下，为了节省内存，我们手动移动了一个粒子并降低了网格大小。我们将底部结构的厚度设置为 40 nm。图 11a、b 分别显示了该结构的透射率和消光比光谱。与第一个模型类似，消光比光谱具有 10,000 量级的峰值，并且不会显着退化。在纳米颗粒的存在下也出现了红移峰。这些特征也与第一个模型中观察到的相同，但与退化特性和蓝移的实验结果不一致。

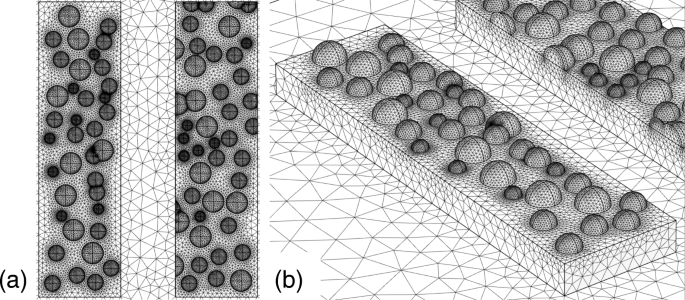
一 顶视图和b 使用随机分布的纳米颗粒建模的粗糙表面的鸟瞰图

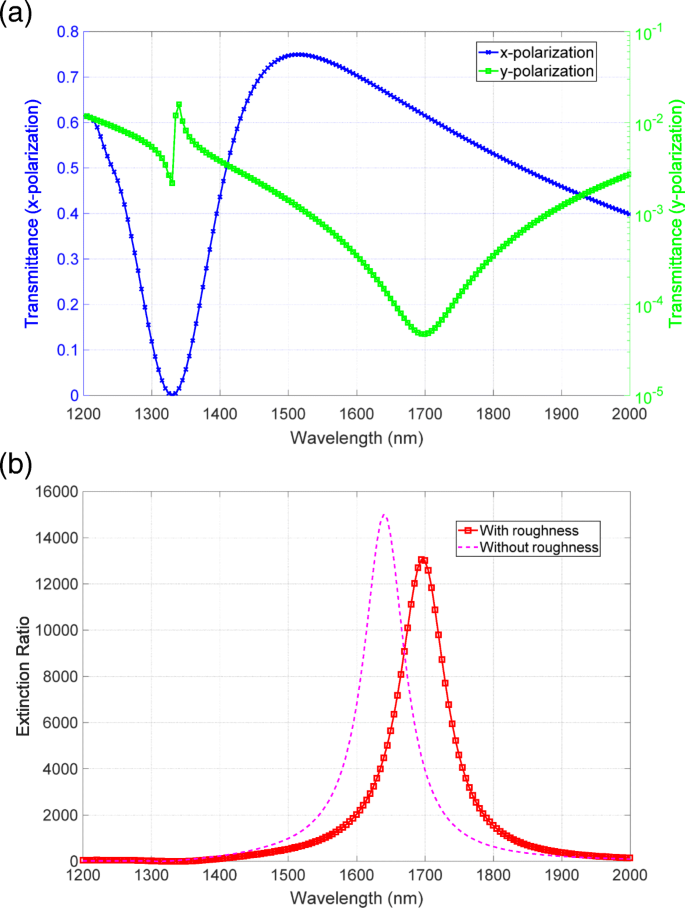
一 透射率和b 图10所示的第二种模型的消光光谱

在这个阶段，我们已经在数值上表明表面形态的变化不会显着降低超表面偏振器的性能。形态学的这种稳健性归因于 Babinet 原理。巴比涅原理不是指表面形态，而是指互补结构的屏幕。基于此原理的高性能偏光片不受形态的强烈影响，因为即使存在表面粗糙度，屏幕也是不变的，从而导致形态的鲁棒性。因此，作为降解的根源，我们需要考虑表面形态的另一个影响。在这里，我们关注与形态相关的金属损失。随着表面粗糙度的增加，由于表面散射和晶界效应，Ag 的虚部增加 [36, 37]。这种损耗的增加可以用描述为 γ 的 Drude 模型的阻尼常数来解释 =ρ n e ² /米 e, 其中 ρ , n , e , 和 m e 分别是电阻率、电子密度、电子电荷和有效电子质量。电阻率由两项组成。一种是体电阻率，另一种是表面电阻率。表面电阻率ρ s 与横向相关长度成反比 ξ ，即 ρ s∝ξ ⁻¹ [38]。随着粗糙度的增加，横向相关长度ξ 降低，从而导致更高的表面电阻率和金属损失。由于使用了周期性边界条件并假设了粗略的周期性结构，因此计算中不包括该物理机制。我们考虑金属损耗增加对消光比的影响，并按如下方式修改 Ag 的介电常数：

其中 ε Ag是从[32]得到的Ag的介电常数，C 是代表金属损耗增加的常数，i 表示虚数单位。请注意，介电常数的实部必须随着虚部的增加而修改，因为实部和虚部通过 Kramers-Kronig 关系连接。在这项研究中，我们只修改了虚部以进行定性讨论。使用这个修正的介电常数，我们计算消光比谱。这个结果如图 12 所示，其中常数 C 从 1 到 5 变化。随着金属损耗的增加，消光比急剧下降。此外，随着损失的增加，光谱的峰值位置表现出蓝移特征。这些急剧退化和蓝移的特征与实验观察到的特征非常吻合。这种蓝移的起源阐明如下。随着金属损耗的增加，低透光率的下降值逐渐变浅。结果，高透射率的峰值对消光比的贡献增加。峰值位置对金属损耗具有很强的不敏感性，并且处于比倾角位置更短的波长处，导致消光光谱的蓝移。因此，我们发现虚部的增加是导致退化的关键因素。

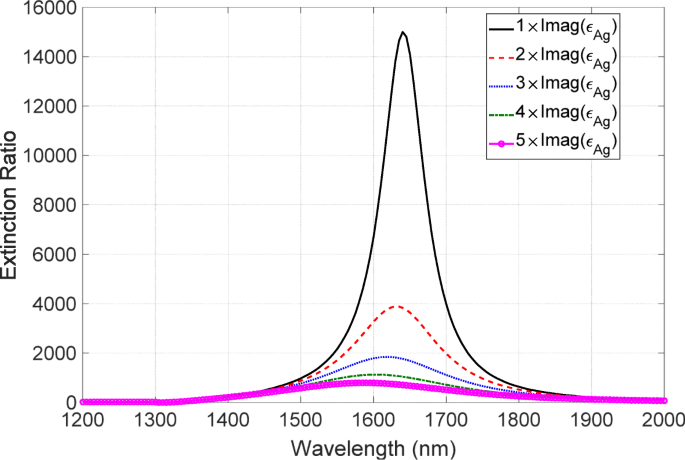
消光光谱的金属损耗依赖性。黑、红、蓝、绿、品红线对应C的情况 =1,2,3,4,5 分别

我们建议通过改变互补金属层的厚度来提高消光比。高透射率的峰值位置位于比低透射率的下降位置更短的波长处。为了提高消光比，这些峰和谷的位置应该彼此靠近。根据巴比涅原理，波峰和波谷必须在同一波长上。然而，该原理假设互补结构包括具有无限薄厚度的完美电导体，即使在近似下也难以在光学区域中验证。结果，互补结构具有不同的共振波长。为了调整波长，我们考虑负责共振的本征模式的特性。图 13a、b 分别显示了图 6 所示透射率峰值和下降位置处的电场和磁场分布图。这些场分布在 z 中描述 -x y 处的平面 =0，在1W入射光强度下。高透光率的本征模在顶部金属结构中具有电偶极子的特性，而低透光率的本征模在底部结构中具有磁环特性。高透射率的共振波长由 z 中的气孔宽度决定 -x 飞机。这是一个固定参数，无法调整。另一方面，低透射率的共振波长由 z 中底部结构的横截面决定 -x 飞机。这可以通过改变金属厚度来调节。这些调整与透射率的厚度依赖性一致，即高透射率的峰值位置对底部金属层的厚度具有低灵敏度，而低透射率的倾角位置具有高灵敏度。基于此分析，我们调整波长如下。随着厚度的增加，横截面增加，低透射率的共振波长向更短的波长移动。结果，波峰和波谷位置变得接近并且消光比增强。为了证实这一点，我们计算了透射率和消光比光谱对厚度的依赖性。在此计算中，我们将顶部金属层的厚度固定为 45 nm。图 14a 显示了 x 的透射光谱 和 y 极化。随着厚度的增加，低透射率的倾角位置向更短的波长移动，并且倾角变得更深。另一方面，即使峰值降低～ 5%，高透射率的峰值位置也不会受到厚度变化的强烈影响。图 14b 显示了消光比光谱。当厚度为35或40nm时，低透射率的下降比45nm的下降更浅，导致消光比较低。当厚度为 50 或 55 nm 时，几乎没有增强。这是因为高透光率峰值的降低抵消了调整峰谷位置的增强作用。当厚度为 60 或 65 nm 时，消光比有明显的提高。这是由于更深的倾角值和位置调整的增强的组合。正如我们在数值上显示的那样，可以通过调整互补金属结构的厚度来进一步提高消光比。这种变化的厚度可以通过重复金属沉积来实现。首先，金属沉积厚度为a 在图案化的基板上进行。然后，用干净的布擦拭，仅去除金属厚度为a的基材表面的顶部金属层 .随后，金属沉积厚度为b 是对样品进行的。结果，顶层和底层的厚度变为b 和 a +b , 分别。

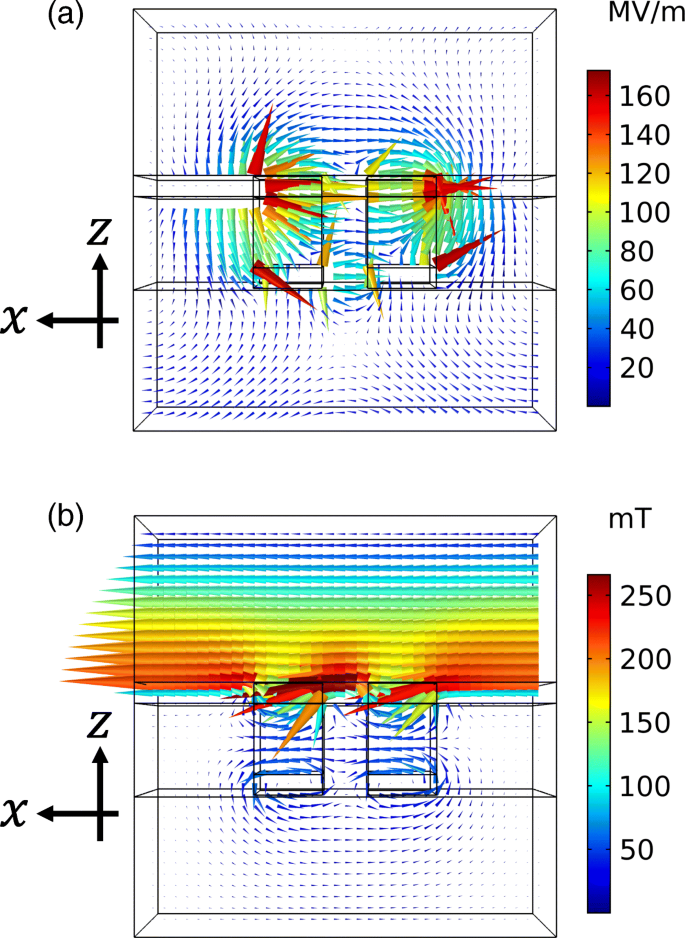
一 高透光率峰值处的电场分布图如图6所示。b 图 6 低透光率倾角处的磁场分布图。伪色表示矢量场强度

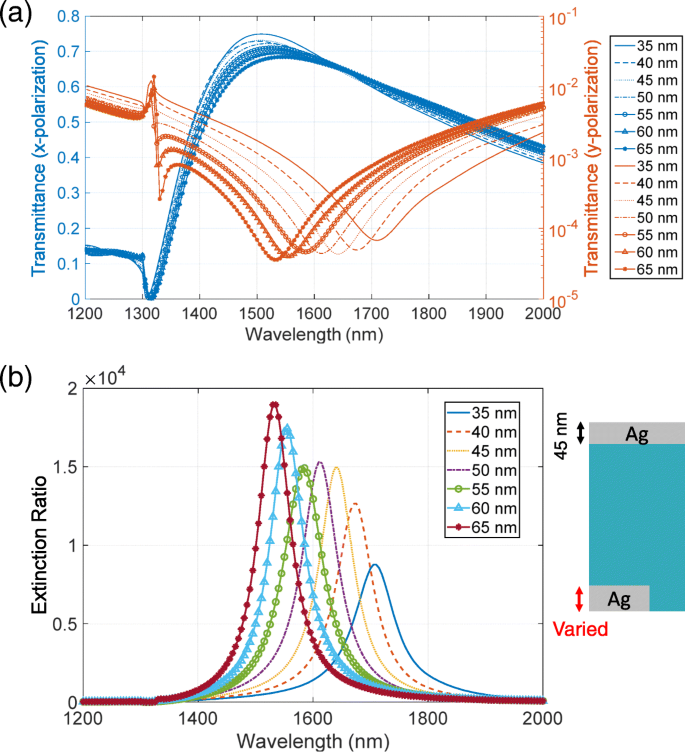
一 透射率和b 当互补金属层具有不同厚度时的消光比光谱。顶部金属层的厚度固定为 45 nm，而底部金属层的厚度从 35 到 65 nm 以 5 nm 的步长变化（参见 b 中的插图 )

结论

我们研究了高性能超表面偏振器的降解特性。制备的超表面表现出 10,000 量级的高消光比。我们注意到高性能已经逐渐下降。为了阐明这种降解的起源，我们研究了表面形态对消光比的影响。提出了两种模型来描述表面形态。一种通过周期曲线和高斯白噪声的组合来模拟粗糙表面，而另一种则通过随机分布的纳米粒子来模拟表面。两种模型都表明高性能不会因表面粗糙度而降低。这是因为高消光比受巴比涅原理支配，导致表面形态的鲁棒性。 We have also investigated the relation between the extinction ratio and the increase in metallic loss because of the surface roughness, which showed drastic degradation of the extinction ratio. The spectral feature of the blue-shift was also reproduced by the numerical calculation, indicating that the degradation is due to the increase in the metallic loss. From this result, we find that the metal deposition should be conducted to reduce the scattering and grain boundary losses that are related to the roughness. Throughout the numerical calculation, we have found that the low transmittance has a high sensitivity to the surface morphology, while the high transmittance does not have the high sensitivity. By utilizing these findings, we proposed that the extinction ratio can be enhanced by varying the thicknesses of the metallic layers. This study paves a way for the development of a metasurface with a high performance and stability toward time degradation.

缩写

BS:

Beam sampler

GLP:

Glan-laser prism

NDF:

Neural density filter

OPO:

Optical parametric oscillator

PhC:

Photonic crystal

SEM：

扫描电子显微镜

YAG:

Yttrium iron garnet