增强对散装狄拉克半金属-绝缘体-金属波导中太赫兹表面等离子体激元的限制

背景

在过去的几十年中，太赫兹 (THz) 波因其创新应用而得到广泛见证，例如太赫兹成像、生化传感和通信 [1,2,3]。为了提高太赫兹器件的传感灵敏度、成像分辨率和集成度，迫切需要将太赫兹波限制在深亚波长范围内 [4,5,6]。表面等离子体激元 (SPP)，即由贵金属导带中的电子与可见光波长中的光子之间的相互作用激发的表面电磁模式，沿金属-绝缘体界面传播，并使光的操控超出经典衍射极限 [7]。 Sommerfeld-Zenneck 模式是可见波段 SPP 的模拟，可以由太赫兹区域的金属支持。超材料和其他人造结构，例如周期性贴片、穿孔板和黄铜管，已被提议用于定制这种松散结合的表面波 [8,9,10]。遗憾的是，该模式的限制性差、固有损耗高和无源可调性严重阻碍了其实际应用。

石墨烯等离子体具有相对低的损耗、动态可调性和对太赫兹波的极端限制，在高分辨率、超紧凑和动态可调设备中具有广阔的应用前景。段等人。提出了一种宽带栅极可调石墨烯异质结构，以相干地产生和控制具有动态可调性和更高效率的太赫兹等离子体。由于石墨烯等离子体场的严格限制，可以生成稳健的差频信号 [11]。段等人。首先研究在太赫兹波长下介电石墨烯等离子体波导阵列中的离散 Talbot 效应，这为纳米级太赫兹波的高分辨率自成像提供了一个新平台 [12]。林等人。提出了一种超紧凑的等离子体诱导透明波导，它有望在太赫兹波的慢光中得到潜在的应用 [13, 14]。李等人。提出了一系列基于 2D 材料等离子体的功能性光学滤波器和吸收器，它们表现出高集成 [15]、低损耗和动态可调性 [16,17,18]。从这些工作中，我们可以确信是表面等离子体的极端限制使得在深亚波长尺度上操纵太赫兹波成为可能。

最近，块体狄拉克半金属（BDS）“3-D 石墨烯”因其高达 9 × 10 ⁶ 的超高载流子迁移率而备受关注。 厘米 ² V ⁻¹ s ⁻¹ ，远高于最佳石墨烯的2 × 10 ⁵ 厘米 ² V ⁻¹ s ⁻¹ [19]。一般来说，载流子迁移率越高，等离子体的固有损耗越低。此外，BDS 的介电函数可以通过改变其费米能量来主动调整。好消息是BDS，如Na3Bi[19]、Cd3As2[20]和AlCuFe准晶[21]，与石墨烯相比更容易加工且更稳定，有望成为继石墨烯之后的新一代等离子体材料.然而，BDS-绝缘体界面中SPPs的模式限制并不乐观。我们最近的工作研究了双层 BDS 片波导中太赫兹 SPP 的操纵，这表明对称耦合模式比单层 BDS 薄膜中的等离子体波导模式具有更好的限制 [22]。对称模式的模式指数在 1.0 THz 时为 1.21，具有 BDS E 的费米能​​量 F =70 meV，仍不能满足深亚波长范围内处理太赫兹波的需求。

在本文中，我们提出了一种深亚波长 BDS 绝缘体金属 (BIM) 波导，具有增强的限制、相对较低的损耗和理想的可调性。研究了这种高度受限模式的色散关系、传播损耗和滤波应用。有趣的是，有一个优化的频率范围，具有增强的限制和减少的损耗，这在金属结构的传统 SPP 模式中很少报道。高达 λ 的宽带模式限制 0/15，损耗相对较低，为 1.0 dB/λ 0 可以实现。与之前研究的基于 BDS 的结构不同，这种 BIM 波导的模式可以有效地通过宽度小于 λ 的超窄狭缝传输 0/2000。以两根硅带作为反射镜，实现了动态可调光谐振腔。通过改变BDS的费米能量可以动态调谐谐振器的谐振频率，在太赫兹开关和滤波方面具有应用前景。

理论与仿真

拟议的 BIM 等离子体波导如图 1(a) 所示，其中厚度为 0.2 μm 的单层 BDS 膜放置在间隙宽度 g 远离由介电间隔物隔开的银基板，介电常数为ε r .太赫兹区域的银衬底可以被视为完美的电导体（PEC）边界。对于 TM 偏振入射光，限制在金属-绝缘体界面的等离子体波导模式可以沿 x 传播 具有波矢 k 的方向 SPP 和沿 y 指数衰减 方向进入自由空间。通过结合适当的边界条件，波矢k BIM 波导的 SPP 可由以下色散关系获得：[23]。

其中 k 0 是入射光的波矢。通过求解方程。 (1)，我们可以得到有效折射率n eff =k SPP/k 0 =Re(n eff) + i 我(n eff) 提出的等离子体波导。对于高度受限的等离子体波导模式，有效折射率 Re(n eff) 粗略描述模式限制，而虚部 Im(n eff) 与模式传播损耗成正比：较大的 Re(n eff) 是，限制越高。当 g 足够大使得 tanh[g (k SPP ² − ε r k 0 ² /ε 0)] ~ 1，方程。 (1) 将简化为色散关系

它描绘了仅由单层 BDS 支持的等离子体波导模式。 BDS的复电导率在方法方程（3）-（4）中给出。

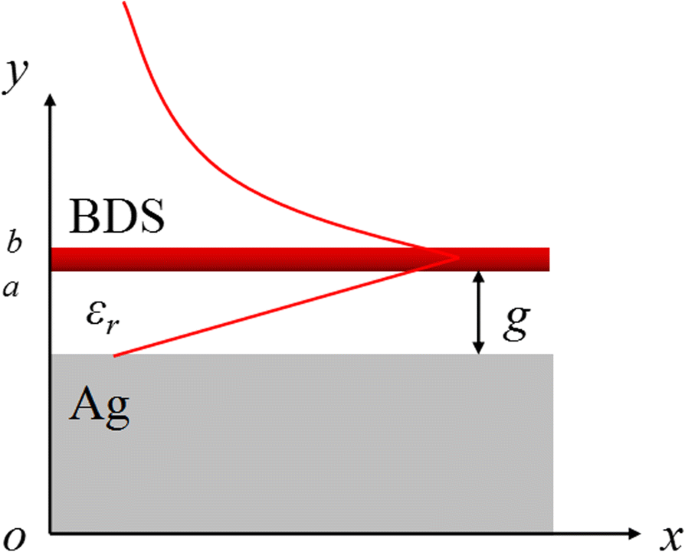
BIM 等离子体波导示意图：以间隙宽度 g 放置单层 BDS 薄膜 远离由介电间隔物隔开的银基板，介电常数为 ε r . TM 偏振等离子体波导模式沿 x 传播 方向并沿 y 衰减 方向。 E 的示意图 x 分布用红线表示

结果与讨论

首先，我们证明了 BIM 波导的模式限制和传播损耗对 BDS 金属间隙宽度的依赖性 g 和费米能量 E F. 通过取 E F =70 meV，我们计算了 SPP 波导模式 n 的有效折射率 g 不同值的 eff , 其中它的实部和虚部, Re(n eff) 和 Im(n eff)，分别绘制在图 2a、b 中。如图 2a 所示，g 的曲线 =10 和 100 μm 在高于 0.05 THz 的频率处合并，这表明等离子体波导模式被严格限制在 BDS-绝缘体界面中，以至于大多数 SPP 场分布在 10 μm 的范围内并且银不起作用在如此大的间隙宽度下。而在间隙宽度 g 之后，模式限制显着增强 从 1 μm 逐渐减小，g 越小 研究，可以获得更强的约束。在传播损耗对间隙宽度g的依赖性中可以观察到类似的趋势 ，如图 2b 所示。另一方面，对于小于 1 μm 的固定间隙宽度，Re(n eff) 每个最初表现出显着减少到最小值，然后表现出逐渐增加的行为，而 Im(n eff) 每个都随着频率的增加而单调减少。因此，存在一个优化的频率区域，其中模式限制强烈增强，而传播损耗逐渐降低。在金属-绝缘体界面的传统等离子体波导模式中很少观察到这种特性。图 2c、d 描绘了模式限制和传播损耗对费米能量 E 的依赖性 BDS薄膜的F，其中间隙宽度g =1μm。与单层和双层波导的情况类似，随着费米能量的增加，模式限制和传播损耗不断降低，这可归因于 BDS 的金属丰度增强和载流子弛豫时间延长。例如，等离子体波导模式在 2.5 THz 处的限制因子可达 λ 0/15，其中 λ 0 入射波长，损耗相对较低，为 1.0 dB/λ 当 BDS 金属间隙宽度为 10 nm 且费米能量为 70 meV 时为 0。因此，依赖上面已经讨论过的框架将增加模式限制，损耗相对较低，可用于集成滤光器、缓冲器和马赫-曾德干涉仪的设计。

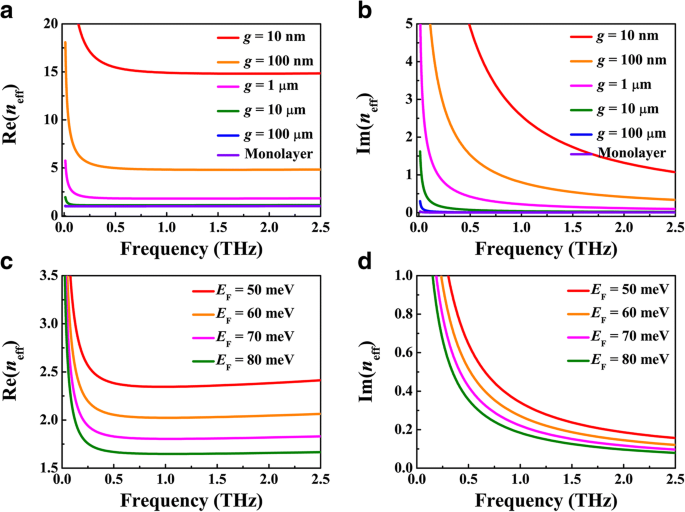
有效折射率的实部和虚部n a 的效果 , b 不同的间隙宽度g , 其中 BDS 的费米能​​量固定为 E F =70 meV，并且 c , d 费米能量 E 的不同值 F，其中间隙宽度固定为 g = 1 微米

为了检查上述分析，我们对所提出的波导结构的传输强度和场分布进行了数值计算。模拟设置在方法中描述。与具有相同费米能量E的单层BDS波导比较 F =70 meV，BIM波导在1.56 THz频率下的传输强度为0.97，高于前者，如图3a所示，这表明BIM结构中的等离子体波导模式具有较低的传播损耗.另一方面，如图 2a 所示，BIM 在 1.56 THz Re(n eff) =2.45，远高于单层情况下的1.002。为了形象化这个陈述，磁场 Hz 这些模式的分布如图 3b、c 所示。可以清楚地发现，BIM 波导中高度受限的等离子体模式显示出比单层 BDS 情况下更短的振荡周期。此外，大部分等离子体场都位于这种狭缝中~λ 0/2000，在非线性物理的近场增强方面具有广阔的应用前景。

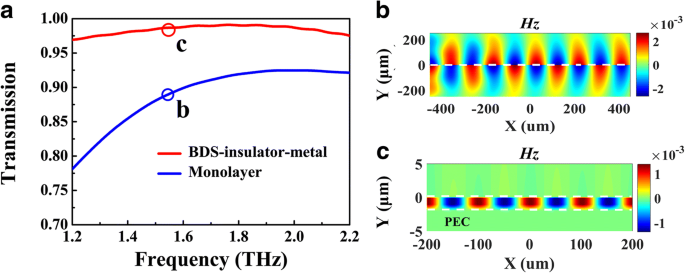
透射光谱的数值计算 (a ) 和磁场 (H z) 分布 (b , c ) BIM（红色曲线）和单层（蓝色曲线）波导，其中 E F =70 meV, g =50 μ m，入射频率为 1.56 THz

在上述所有应用中，光谐振器是定制太赫兹等离子体波导模式的基本元件。如图 4a 所示，两个硅 (n Si =3.4) [24] 带嵌入介电隔离物以形成反射镜，其中传播的等离子体波可以在硅 - 空气界面来回反射，在两个硅之间的 BIM 区域形成局部驻波共振丝带。只有入射频率满足驻波的谐振条件，等离子体波才能通过与设计的光谐振器耦合传输到波导的输出端。图 4a 显示了具有两个硅带的 BIM 波导的传输光谱，其中在 1.56 和 2.22 THz 的频率处可以明显地发现具有 0.12 和 0.09 THz 的 FWHM（半峰全宽）值的两个传输峰值，这证明了新颖性太赫兹区域的带通滤波效果。磁场分布 (|H z| ² ) 的传输峰值如图 4c、e 所示，这意味着夹在两个硅带之间的 BIM 区域可以被视为法布里-珀罗 (FP) 腔。在 FP 腔中可以清楚地发现一阶和二阶共振。共振频率附近的入射等离子体波可以耦合到 FP 腔中，然后通过 BIM 波导传输，从而在光谱中产生传输峰值。而对于非谐振频率区域，无法形成驻波，因此在 BIM 波导的左端口禁止入射波，如图 4d 所示。此外，结合BIM波导的色散关系，可以通过耦合模式理论（CMT）[17]解析计算传输强度：

其中 ω 0 分别是 FP 腔的谐振频率。在这里，κ w =ω 0/(2Q w ) 和 κ 我 =ω 0/(2Q 我 ) 分别是与 FP 腔的波导耦合损耗和固有损耗相关的衰减率。可以通过Q来估计总的和内在的损耗品质因数 t =ω 0/FWHM 和 Q 哦 =− Re(n eff)/(2Im(n eff))，分别。然后，从总损耗中减去固有损耗即可得到波导耦合损耗品质因数，即Q ei =Q 哦 问 ti /(Q 哦 - Q ti ) [17]。基于 CMT 的分析结果与数值模拟非常吻合，如图 4b 所示。

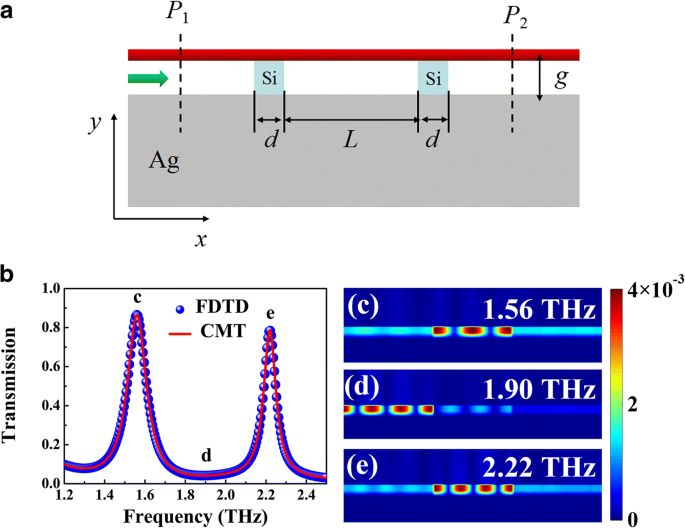
一 引入硅带的 BIM 波导示意图。每条硅带的宽度为d , 色带之间的距离为 L . b 所提出结构的数值（蓝色球）和 CMT 拟合（红色曲线）透射光谱，其中 g =1 μm，d =5 μm 和 L =120 μm。 c –e 磁场分布 (|H z | ² ) 的入射频率为 1.56 (c ), 1.90 (d ) 和 2.22 THz (e )

图 5 显示了谐振频率对腔长 L 的依赖性 , 其中 g =1 μm，d =5 μm，和 E F =70 meV。随着L的增加，透射峰趋于红移 ，如图 5a 所示，可以通过驻波谐振条件 2k 进一步描述 SPP(ω r )L + θ =2mπ (米 =1, 2, 3, ...)，其中 θ 是来自硅-空气界面的反射相移和 k SPP(ω r ) 是谐振频率下 BIM 波导的波矢。如图 5b 所示，随着 L 的增加，第一和第二模式的谐振频率确实表现出红移 .根据方程。 (1)、模式限制受间隙宽度g的影响 因此对谐振频率有影响。图 6a 显示了不同 g 的透射光谱 , 其中 L =120 μm 和 E F =70 meV。随着g的增加 ，相同顺序的共振峰呈现蓝移。这种现象可归因于 Re(n eff)，如图 6c 所示。 BDS的费米能的调节在实验中可以通过碱性表面掺杂来实现。图 6b 显示了不同费米能量的透射光谱，其中其他参数与图 4b 相同。随着费米能量的增加，传输峰值呈现蓝移，这也可能涉及驻波共振图。对于固定长度 L , FP 腔支持具有定义的 SPP 波长 λ 的共振 SPP =λ 0/ Re(n eff)，其中 λ 0 是入射波长。如图 6c 所示，Re(n eff) 随费米能的增加而减小。结果，入射波长λ 0 也应该减少以保持 λ SPP 作为常数。这就是传输峰值随着费米能量的增加而发生蓝移的原因。同时，传输峰值的带宽变窄，这可以归因于 Im(n eff)，即等离子波导模式在BIM波导中的传播损耗。

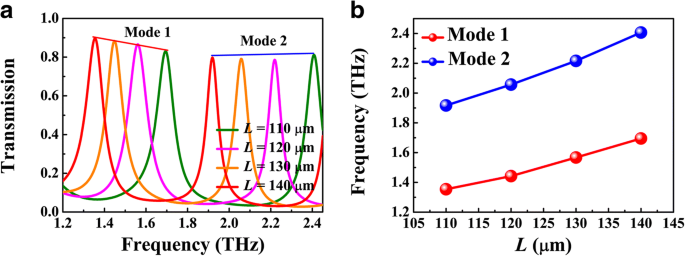
一 不同腔长L的数值透射光谱 . b 模式 1 和模式 2 的谐振频率作为腔长度的函数 L .在这里，g =1 μm，d =5 μm，和 E F =70 meV

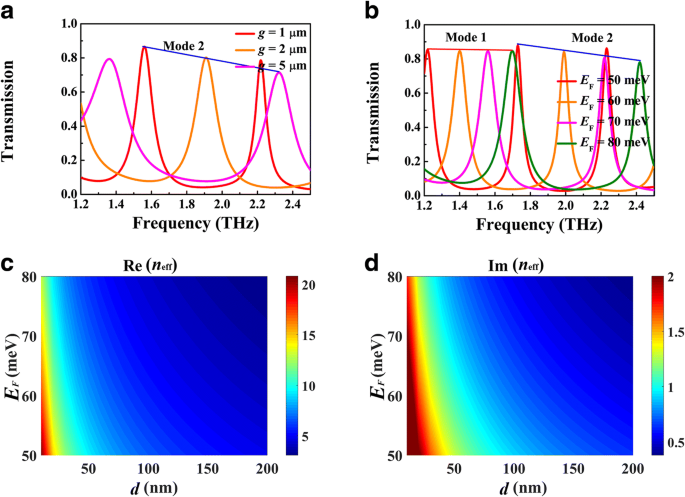
不同间隙宽度g的透射光谱 (a ) 和费米能量 E F (b )，其中其他参数与图 4b 相同。 Re(n的依赖 效果) (c ) 和 Im(n eff) (d ) 费米能量 E F和间隙宽度g

结论

总之，我们已经展示了由 BIM 波导支持的高度受限的太赫兹等离子体模式。模式限制和损耗特性与 BDS-金属分离和费米能量的变化进行了讨论，这表明存在一个优化的频率范围，模式限制增强，传播损耗降低，这在传统的 SPP 模式中很少报道在金属结构中。与之前研究的基于 BDS 的结构不同，这种 BIM 波导的模式可以在宽度小于 λ 的非常窄的狭缝中得到有效支持 0/2000。以两根硅带为反射镜，实现了动态可调带通滤波器，通过调整BDS薄膜的费米能量，无需重新优化其结构参数即可主动控制谐振频率。

方法

数值结果是通过使用二维有限差分时域 (FDTD) 方法获得的，其中完美匹配层被设置为吸收 x 中的散射光 和 y 方向。 BDS 薄膜的网格尺寸设置为 dx × dy =1μm × 0.02μm，以达到良好的收敛性。

BDS的频率相关电导率用Kubo公式描述，随机相位近似[12, 25]。

其中 G (E ) =n (-E ) − n (E ) 和 n (E ) 是费米-狄拉克分布函数，E F 是 BDS 的费米能​​量，k F =E F/ћv F 是它的费米动量，v F =10 ⁶ m/s 是费米速度。 ε =E/E F, Ω =ћω/E F+ iћτ ⁻¹ /E F, 其中 ћτ ⁻¹ =v F/(k Fμ ) 是电子散射率，它显示出对载流子迁移率 μ 的强烈依赖性。 ε c =E c /E F (E c 是 Dirac 谱不再是线性的截止能量），并且 t 是量子简并因子。以AlCuFe为例，我们计算中的拟合参数设置如下：t =40, ε c =3, μ = 3 × 10 ⁴ 厘米 ² V ⁻¹ s ⁻¹ 和 E F =70 meV。

本研究不涉及人类参与者、数据、组织或动物。

缩写

BDS：

散装狄拉克半金属

BIM：

BDS-绝缘体-金属

CMT：

耦合模式理论

FDTD：

有限差分时域

FWHM：

半高全宽

SPP：

表面等离子体激元