Minterm vs Maxterm 解决方案
到目前为止,我们一直在寻找逻辑归约问题的总和 (SOP) 解决方案。对于这些 SOP 解决方案中的每一个,还有一个总和解决方案 (POS),这可能更有用,具体取决于应用程序。
在使用乘积解决方案之前,我们需要介绍一些新术语。以下用于映射产品术语的过程对本章来说并不陌生。
我们只是想建立一个minterms的正式程序,以便与maxterms的新程序进行比较。
小项
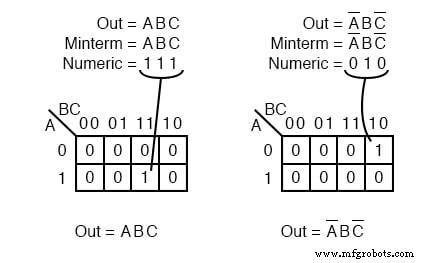
minterm 是一个布尔表达式,结果为 1 对于单个单元格的输出,0 s 表示卡诺图或真值表中的所有其他单元格。如果一个 minterm 有一个 1 其余单元格为 0 s,它似乎覆盖了 1 的最小区域 s.
左上图显示了 minterm ABC , 单个产品术语,作为单个 1 在否则 0 的地图中 s。我们还没有显示 0 到目前为止,我们的卡诺图中的 s,因为除非特别需要,否则通常会省略它们。另一个 minterm A'BC' 显示在右上方。
要审查的一点是单元格的地址直接对应于被映射的 minterm。也就是说,单元格 111 对应于 minterm ABC 左上角。
在右上方我们看到最小项 A'BC' 直接对应于单元格 010 .一个布尔表达式或映射可能有多个最小项。
参考上图,我们总结一下在K-map中放置一个minterm的过程:
- 确定要映射的最小项(乘积项)项。
- 写出相应的二进制数值。
- 使用二进制值作为地址放置1 在 K 图中
- 对其他最小项(乘积总和中的 P 项)重复步骤。
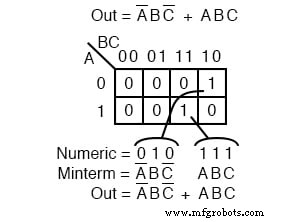
如上所示,布尔表达式通常由对应于卡诺图中多个单元格的多个最小项组成。此图中的多个最小项是我们在上图中检查的单个最小项。
我们回顾以供参考的一点是 1 s 作为二进制单元地址从 K-map 中出来,直接转换为一个或多个乘积项。
直接我们的意思是 0 对应一个补变量,一个1 对应一个真实的变量。示例:010 直接转换为 A'BC' .
在这个例子中没有减少。不过,我们确实有一个来自 minterms 的 Sum-Of-Products 结果。
参考上图,让我们总结一下从 K-map 写出 Sum-Of-Products 简化布尔方程的过程:
- 形成最大的 1 组 可能涵盖所有最小项。组必须是 2 的幂。
- 为组写入二进制数值。
- 将二进制值转换为乘积项。
- 对其他组重复步骤。每个组在 Sum-Of-Products 中产生一个 p 项。
到目前为止,没有什么新鲜事,已经写下了处理 minterms 的正式程序。这是处理 maxterms 的一种模式。
接下来我们攻击0的布尔函数 对于单个单元格和 1 s 为所有其他人。
最大值
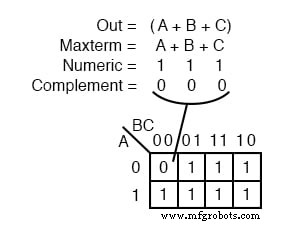
一个 maxterm 是一个布尔表达式,结果为 0 对于单个单元格表达式的输出,1 s 表示卡诺图或真值表中的所有其他单元格。左上图显示了 maxterm (A+B+C) , 单个求和项,作为单个 0 在否则 1 的地图中 s.
如果 maxterm 有一个 0 其余单元格为 1 s,它似乎覆盖了 1 的最大区域 s.
现在我们正在处理一些新的东西,maxterms,有一些差异。 maxterm 是 0 ,不是 1 在卡诺图中。 maxterm 是求和项,(A+B+C) 在我们的示例中,不是产品术语。 (A+B+C) 看起来也很奇怪 映射到单元格 000 .
对于方程 Out=(A+B+C)=0 , 所有三个变量 (A, B, C) 必须分别等于 0 .只有(0+0+0)=0 将等于 0 .因此,我们将唯一的 0 对于 minterm (A+B+C) 在单元格 A,B,C=000 中 在 K-map 中,输入都是 0 .
这是唯一会给我们一个 0 的情况 对于我们的 maxterm。所有其他单元格包含 1 s 因为除了 ((0,0,0) 之外的任何输入值 对于 (A+B+C) 产量 1 s 在评估中。
参考上图,在K-map中放置一个maxterm的过程是:
- 确定要映射的总和项。
- 写出对应的二进制数值。
- 形成补语
- 使用补码作为地址来放置 0 在 K 图中
- 对其他 maxterms 重复此操作(Product-of-Sums 表达式中的 Sum 项)。
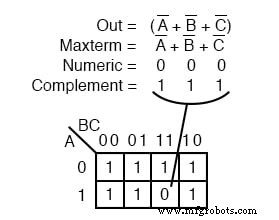
另一个 maxterm A'+B'+C' 如上所示。数字 000 对应于 A'+B'+C' .补码是111 .放置一个 0 对于 maxterm (A'+B'+C') 在这个单元格中 (1,1,1) 如上图所示。
为什么要(A’+B’+C’) 导致 0 在单元格 111 中 ?当 A'+B'+C' 是 (1’+1’+1’) , 全部 1 s in,即 (0+0+0) 取补码后,我们有唯一条件可以给我们 0 .所有1 s 与所有 0 互补 s,即 0 当 OR 编辑。
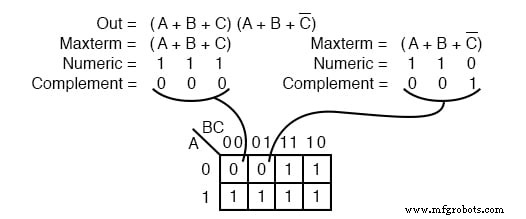
一个布尔乘积表达式或映射可能有多个 maxterms,如上所示。 Maxterm (A+B+C) 产生数字 111 与 000 互补 , 放置一个 0 在单元格 (0,0,0) 中 . Maxterm (A+B+C’) 产生数字 110 与 001 互补 , 放置一个 0 在单元格 (0,0,1) 中 .
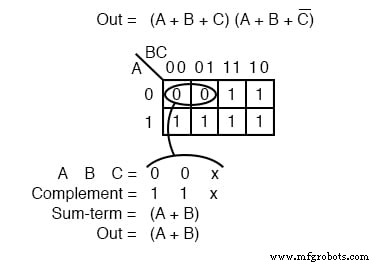
现在我们有了 k-map 设置,我们真正感兴趣的是展示如何编写一个 Product-Of-Sums 约简。形成 0 s 分组。那将是以下两人一组。写出和项对应的二进制值是 (0,0,X) .
A 和 B 都是 0 为组。但是,C 都是 0 和 1 所以我们写一个 X 作为 C 的占位符 .形成补码 (1,1,X) .写出和项(A+B) 丢弃 C 和 X 它占据了它的位置。
一般而言,期望在总和结果中将更多的总和项相乘。不过,我们这里有一个简单的例子。
让我们总结一下为 K-map 编写 Product-Of-Sums 布尔归约的过程:
- 形成最大的 0 组 s 可能,涵盖所有 maxterms。组必须是 2 的幂。
- 为组写入二进制数值。
- 补充组的二进制数值。
- 将补值转换为和项。
- 对其他组重复步骤。每个组在总和结果中产生一个总和项。
例子
示例:
简化下面的 Product-Of-Sums 布尔表达式,以 POS 形式提供结果。
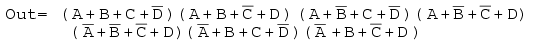
解决方案:
将七个 maxterm 作为 0 转移到下面的地图中 s。一定要补充输入变量以找到合适的单元格位置。
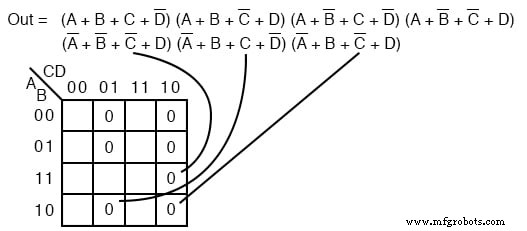
我们映射 0 s 因为它们在上面的地图上从左到右从上到下显示。我们用引导线定位最后三个 maxterms..
一旦细胞在上面就位,形成如下所示的细胞组。较大的组将给出输入较少的总和项。较少的组将在结果中产生较少的总和项。
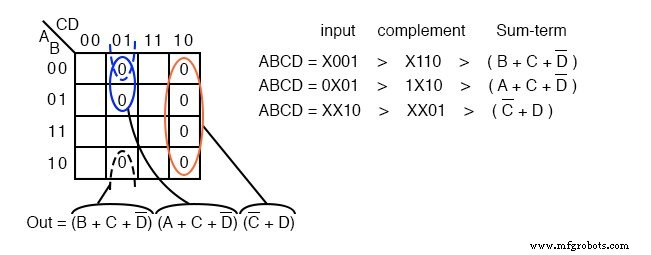
我们有三个组,因此我们希望在上面的 POS 结果中有三个总和项。 4 个单元格的组产生 2 个变量的总和项。两组2-cells给了我们两个3-variable sum-terms。
详细显示了我们如何得出上述总和项。对于组,写入二进制组输入地址,然后对其进行补码,将其转换为布尔和项。最终结果是三个和的乘积。
示例:
简化下面的 Product-Of-Sums 布尔表达式,以 SOP 形式提供结果。
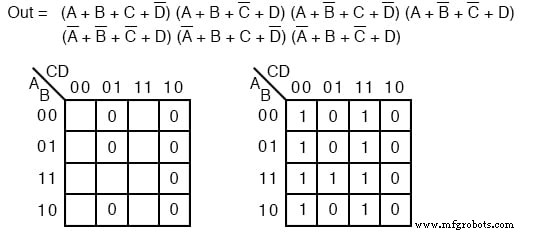
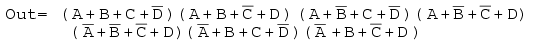
解决方案: 这看起来像是上一个问题的重复。不同的是,我们要求的是 Sum-Of-Products 解决方案,而不是我们刚刚完成的 Product-Of-Sums。映射 maxterm 0 s 来自上一个问题中给出的和的乘积,左下方。

然后填写隐含的1 s 在右上方地图的剩余单元格中。
形成 1 组 s 覆盖所有 1 s。然后按照本章的前一部分编写 Sum-Of-Products 简化结果。这与之前的问题相同。
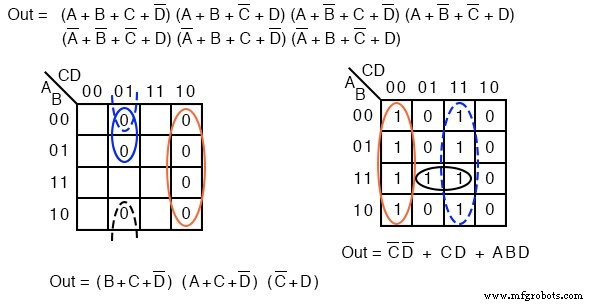
上面我们展示了来自上一个示例的 Product-Of-Sums 解决方案和来自当前问题的 Sum-Of-Products 解决方案以进行比较。
哪个是更简单的解决方案? POS 使用 3-OR 门和 1-AND 门,而 SOP 使用 3-AND 门和 1-OR 门。两者都使用四个门。
仔细观察,我们计算门输入的数量。 POS 使用 8 个输入; SOP 使用 7 输入。根据最小成本解决方案的定义,SOP解决方案更简单。
这是一个技术上正确的答案示例,但在现实世界中几乎没有用。
更好的解决方案取决于复杂性和所使用的逻辑系列。如果使用 TTL 逻辑系列,SOP 解决方案通常会更好,因为与非门是基本构建块,与 SOP 实现配合良好。
另一方面,当使用 CMOS 逻辑系列时,POS 解决方案是可以接受的,因为所有尺寸的 NOR 门都可用。
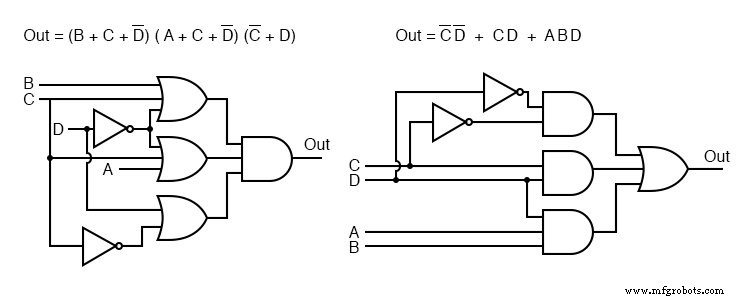
上面显示了两种情况的门图,左为总和,右为总和。
下面,我们仔细看看我们的示例逻辑的 Sum-Of-Products 版本,它在左侧重复。
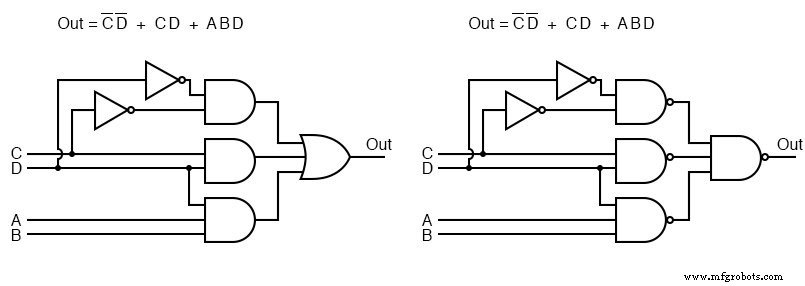
以上所有左侧的与门已被右侧的与非门替换。输出处的或门被替换为与非门。为了证明 AND-OR 逻辑等效于 NAND-NAND 逻辑,将 3-NAND 门输出端的反相反转气泡移动到最终 NAND 的输入端,如从右上方到左下方所示。
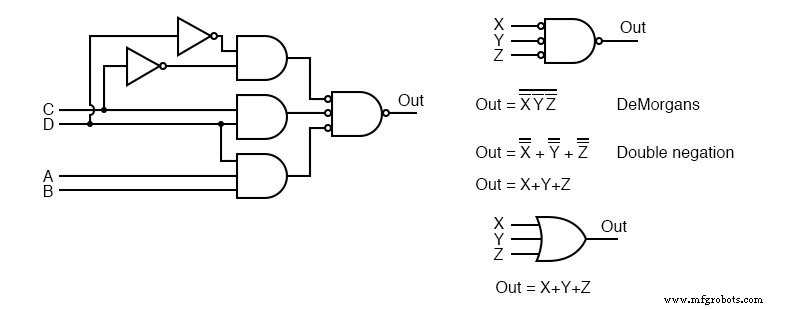
在右上方,我们看到具有反向输入的输出与非门在逻辑上等同于 DeMorgan 定理和双重否定的或门。
此信息可用于在实验室环境中构建数字逻辑,其中 TTL 逻辑系列与非门比其他类型更容易在各种配置中使用。
构造NAND-NAND逻辑代替AND-OR逻辑的流程如下:
- 生成减少的积和逻辑设计。
- 在绘制 SOP 的接线图时,将所有门(AND 和 OR)都替换为与非门。
- 未使用的输入应绑定到逻辑高。
- 在故障排除的情况下,NAND 门输出第一级的内部节点与 AND-OR 图逻辑电平不匹配,而是反转。使用 NAND-NAND 逻辑图。不过,输入和最终输出是相同的。
- 标记任意多个包裹 U1、U2 等
- 使用数据表为所有门的输入和输出分配引脚编号。
示例:
让我们重新审视之前涉及 SOP 最小化的问题。生成总和解决方案。将 POS 解决方案与之前的 SOP 进行比较。
解决方案:
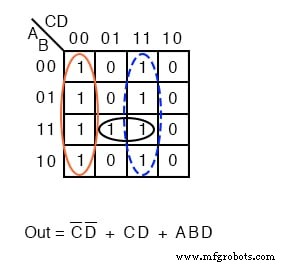
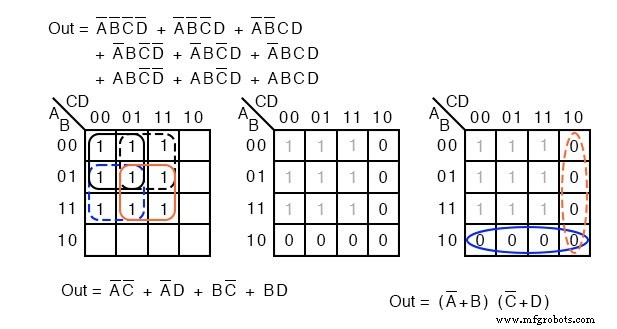
在左上方,我们有一个以 9 分钟布尔非简化表达式开始的原始问题。回顾一下,我们形成了四组 4 细胞以产生 4-product-term SOP 结果,左下。
在上面中间的图中,我们用隐含的 0 填充空格 s。 0 s 形成两组 4 细胞。纯蓝色组是(A’+B) ,红色虚线组为(C’+D) .这会在和的乘积结果中产生两个和项,在右上方 Out =(A'+B)(C'+D)
将之前的 SOP 简化(左)与 POS 简化(右)进行比较,表明 POS 是成本最低的解决方案。 SOP总共使用5个门,POS只使用3个门。
由于结果的简单性,这种 POS 解决方案在使用 TTL 逻辑时甚至看起来很有吸引力。我们可以找到具有 2 个输入的 AND 门和 OR 门。
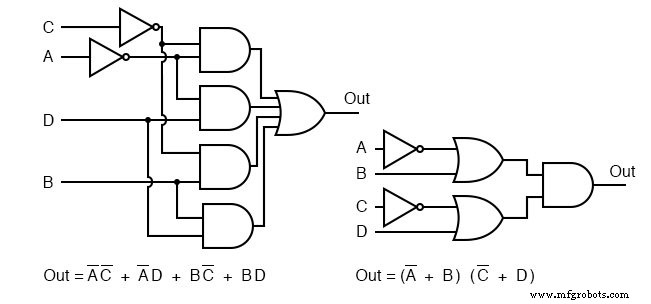
SOP 和 POS 门图如上图所示,用于我们的比较问题。
给定下面 TTL 逻辑系列集成电路门的引脚输出,用电路指示符(U1-a、U1-b、U2-a 等)和引脚编号标记右上方的 maxterm 图。
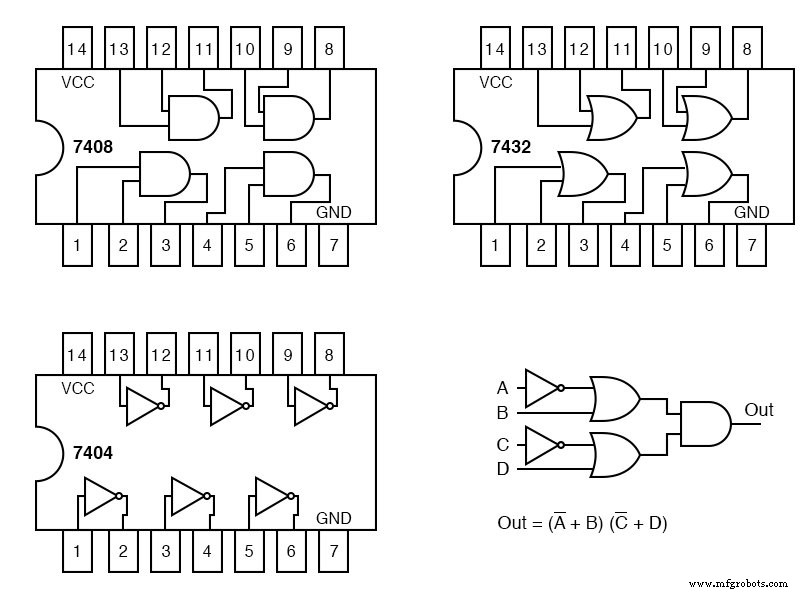
我们使用的每个集成电路封装都会收到一个电路代号:U1、U2、U3。为了区分包装内的各个门,将它们标识为a、b、c、d等。
7404 六角逆变器封装为 U1。其中的各个反相器是 U1-a、U1-b、U1-c 等。 U2 分配给 7432 四或门。 U3分配给7408四与门。
参考上面封装图上的管脚号,我们为下面示意图中的所有门输入和输出分配管脚号。
我们现在可以在实验室环境中构建这个电路。或者,我们可以设计一个印刷电路板 为了它。印刷电路板包含铜箔“布线”,背面是酚醛树脂或环氧玻璃纤维的非导电基材。
印刷电路板用于大量生产电子电路。将未使用的门的输入接地。
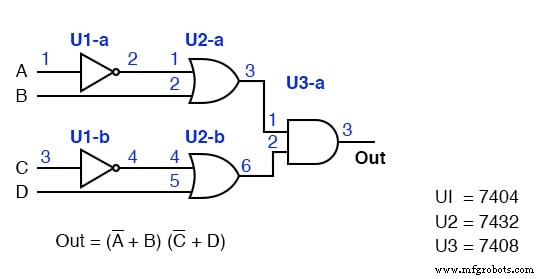
用电路代号和引脚编号标记左上方的先前 POS 解决方案图(背面第三个图)。这将类似于我们刚刚所做的。
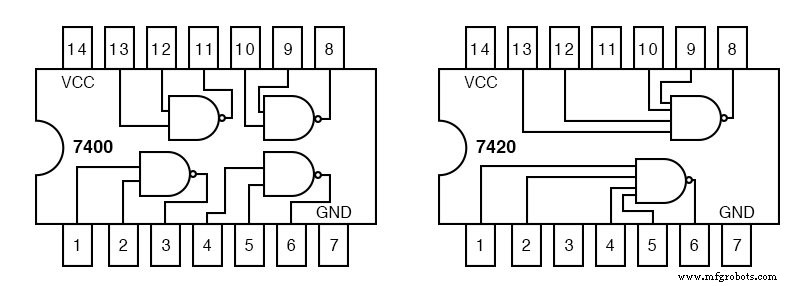
我们可以在前面的示例中找到 2 输入与门,7408。然而,我们很难在我们的 TTL 目录中找到一个 4 输入的 OR 门。
唯一一种具有 4 个输入的门是右上方所示的 7420 与非门。
我们可以通过将 NAND 门的输入反相来将 4 输入与非门变成 4 输入或门,如下所示。因此,我们将通过反转输入将 7420 4 输入与非门用作或门。
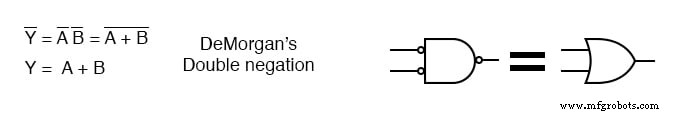
我们不会使用分立反相器来反转 7420 4 输入与非门的输入,而是使用 2 输入与非门来驱动它,而不是 SOP、minterm、解决方案中要求的与门。
2输入与非门输出的反相为4输入或门提供反相。
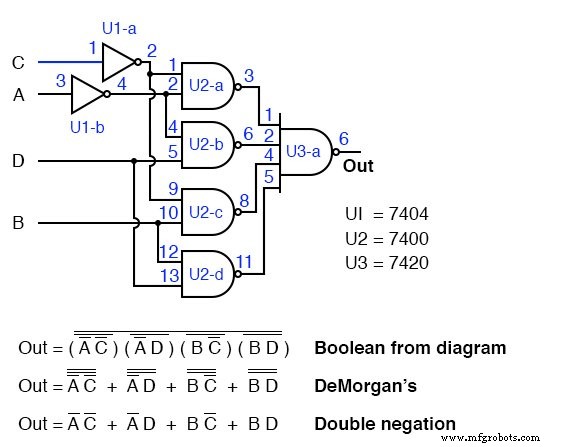
结果如上所示。使用 NAND-NAND 逻辑代替 AND-OR 逻辑,这是用 TTL 门实际构建它的唯一实用方法。
相关工作表:
- 卡诺图工作表
工业技术


