具有热控 RKKY 耦合的纳米结构中的磁滞

背景

Ruderman-Kittel-Kasuya-Yosida（RKKY）型的间接交换耦合（IEC）[1]和巨磁阻效应[2]的重要发现产生了大量新的基础物理成果和大量应用[3]。所发现的 IEC 在幅度和符号上与金属叠层中各个铁磁层的间隔发生振荡，产生平行 (P) 或反平行 (AP) 磁基态。这种 RKKY 类型的相互作用几乎与温度无关 [4, 5] 并且在很大程度上对制造后的任何其他外部控制不敏感，这限制了效果的使用。最近试图增强温度对 RKKY 的影响并用它来控制 Tb/Y/Gd [6] 和 Co/Pt [7] 多层中的 IEC 报告了相对较弱的 RKKY，没有直接平行到反平行（P-to- AP) 热开关，具有广泛的热转变 (~ 100 K)。

我们最近展示了 [8, 9] 磁性多层中层间 RKKY 耦合的异位热控制的新机制。该想法基于使用具有相对较低居里温度 (T C ^* ) 而不是强铁磁 (FM) 层之间的非磁性垫片。在最初的设计中，经典 RKKY 三层 Fe/Cr/Fe 中的 Cr 垫片被稀释合金 Fex 取代 Cr100 − x （图 1a、b）。当垫片在 T 处为顺磁性 (PM) 时> T C ^* （图 1a），由于反铁磁 (AFM) 间接，三层表现出 Fe 矩的反平行排列 交换耦合（RKKY）。平行对齐由 direct 强制执行 当垫片为 FM (T <T C ^* )（图 1b）。随着温度的变化，这些三层表现出平行到反平行的磁化转换，由于磁邻近效应 [10]，具有 ~ 100 K 的相当宽的转变。与具有 制服 的三层相比 间隔，三层不均匀，复合 间隔物表现出显着增强的性能，热磁转变宽度低至~ 10 K。此外，通过调整间隔物特性，可以在 T <T C ^* .在 T 以上加热 C ^* ，Fe 矩将它们的相互方向反转为 Fe/sp1/Fe 平行（图 1d）或 Fe/sp2/Fe 反平行（图 1f）。就实际意义而言，狭窄的热转变和选择磁区（P/AP）以及工作温度区间的能力都是重要的优势。

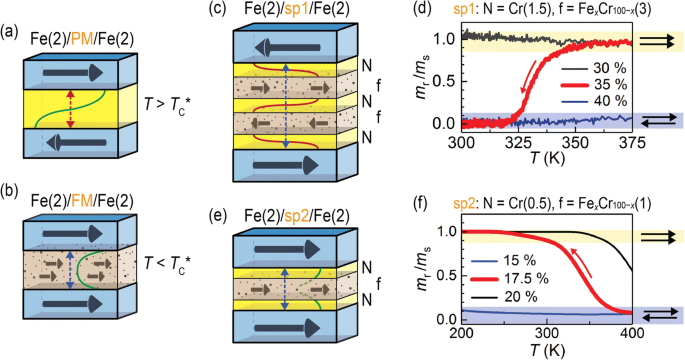
当垫片为顺磁性 (PM) (a ) 或铁磁 (FM) (b ）。 c , e 具有改性复合间隔物 sp1 和 sp2 的结构在低温下分别表现出反平行和平行磁基态 (T <T C ^* ）。 d , f 具有隔离物sp1和sp2的结构的剩余磁化强度的相应特征温度变化对于隔离物内部稀释合金层的不同成分。括号中的层厚以“纳米”为单位

我们多层中的反铁磁层间耦合清楚地表现为零剩磁，反映了 Fe 层矩的反平行排列。除零剩磁外，磁化曲线M (H ) 的特点是在反转场扫描时采用阶梯式的饱和和滞后方法（图 2a）。双线性交换耦合模型给出M (H ) 作为在间接交换的有效场处接近饱和的线，H J .由于结构的铁磁层的面内磁各向异性，饱和的阶梯状特征发生，导致易轴各向异性 [11] 的一个步骤，以及四倍各向异性 [12] 的两个连续步骤。然而，我们对多层膜的角度相关磁力测量和磁谐振研究显示没有宏观面内磁各向异性。后一个事实保证了对实验结果进行更全面的分析，并伴随着模型模拟。在下文中，这种综合方法用于对比两种关键多层设计的磁化转换机制——均匀（图 1a、b）与复合间隔层（图 1c、e）。

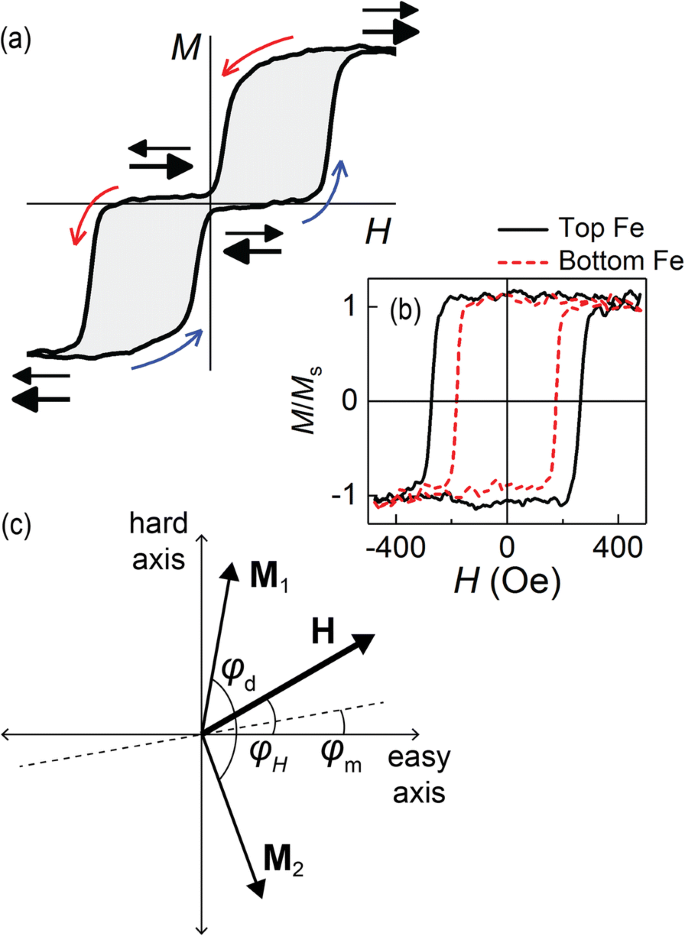
一 典型的面内磁化曲线，M (H )，通过 MOKE 测量具有反铁磁层间耦合的 Fe/sp2/Fe 多层膜。弯曲箭头表示场扫描方向；水平箭头表示 Fe 磁矩的相互对齐。 b MOKE M (H ) 循环参考 Fe(2)/Cr(10)（底部 Fe）和 Cr(10)/Fe(2)（顶部 Fe）双层。 c 平面内M的参考系示意图 1、M 2、H , 相对于纳米微晶双重磁各向异性的易轴

我们指出了理解给定系统中层间交换所涉及的机制的重要性。多层中 RKKY 的开创性工作 [13] 及其扩展到例如双二次交换 [14, 15] 引发了物理和技术的重大发展，即自旋电子学。然而，由于缺乏合适的开关机制，原始形式的 RKKY 在今天不再使用，但通常在设备中起到辅助作用，例如，磁通闭合参考层。在这项工作中，我们研究了这种主要的 RKKY 切换机制，更具体地说，分析了导致 RKYY 热开/关切换的相互作用之间的相互作用，这反过来又控制了磁化的 P/AP 切换效率。纳米结构。基于此分析，我们能够得出优化居里-RKKY纳米器件开关性能的结论和建议。

方法

在这项工作中，我们分析了两个系列的样本：(1) Fe(2)/sp1(x =30–40 at.%)/Fe(2)，其中 sp1 =N/f/N/f/N，N =Cr(1.5)，f =Fe(0.25)/Fex Cr100 − x (3)/Fe(0.25)（图 1c）和（2）Fe(2)/sp2(x =10–20 at.%)/Fe(2)，其中 sp2 =N/f/N，N =Cr(d Cr), f =Fex Cr100 − x (d ), d 总 =(2d Cr + d ) =1.5 nm（图 1e）。此外，沉积了许多参考膜和双层。括号中的厚度以“纳米”为单位。使用直流磁控溅射系统在室温下将多层沉积到 Ar 预蚀刻的未掺杂 Si (100) 基板上。稀释的 Fex 层 Cr100 − x 不同成分的二元合金是使用单独的 Fe 和 Cr 靶的共溅射沉积的。关于多层制造的更多细节可以在别处找到[8, 9]。

使用配备高温炉（Lakeshore Inc.）的振动样品磁力计（VSM）在 295-400 K 的温度范围内进行面内磁表征，以及磁光克尔效应（MOKE）配备光学低温恒温器 (Oxford Instr.) 的磁力计，温度范围为 77-450 K。此外，铁磁共振 (FMR) 测量在室温下使用配备自动测角仪的 X 波段 Bruker ELEXYS E500 光谱仪进行测量磁共振谱的面内角相关性。

结果与讨论

间接交换耦合现象

用于模拟三层 F1/NM/F2 的磁化曲线的现象学静磁模型，其中 F1 和 F2 是铁磁层，NM 是非磁性间隔物，具有以下假设。首先，在薄膜平面上施加磁场，这与我们的实验相对应并简化了计算。其次，多晶薄膜中的单个晶粒具有双重面内各向异性，易轴均匀分布在所有面内角度（薄膜在面内旋转下沉积）。这些假设对于所研究的系统是合理的，并且对测量的 M 产生了最佳拟合 (H ) 不同温度下的数据，如下所述。

我们的 F1/NM/F2 系统的自由能密度可以写为

其中 U H , U a 和 U J 分别是 H 场中 FM 层的塞曼能量 =(H , φ H )、单轴各向异性能量和双线性类型的层间耦合能量 [16, 17]。 FM 层的磁矩，M 1 =(M , φ 1) 和 M 2 =(M , φ 2)，具有相同的量级，如图 2c 所示。 H a1,2 和 H J 分别是单轴（双重）各向异性和双线性层间耦合的有效场。转换为角度变量φ m =(φ 1 + φ 2)/2 和 φ d =(φ 1 − φ 2) 简化系统磁自由能的表达式为

在以下模拟中，磁化曲线 M (H )，通过寻找参数φ得到 m 和 φ d，对应于U的最小值 在（2）中对于给定的φ H , H 1a, H 2a 和 H J ，根据

磁化矫顽力

测量的 M (H ）对于具有 AFM 交换耦合的结构具有阶梯状形状，具有明确定义的反向场扫描矫顽力（图 3a）。上述现象学模型用于分析铁磁层Fe(2 nm)的磁性和介导层间耦合的复合间隔件中的热致磁跃迁。

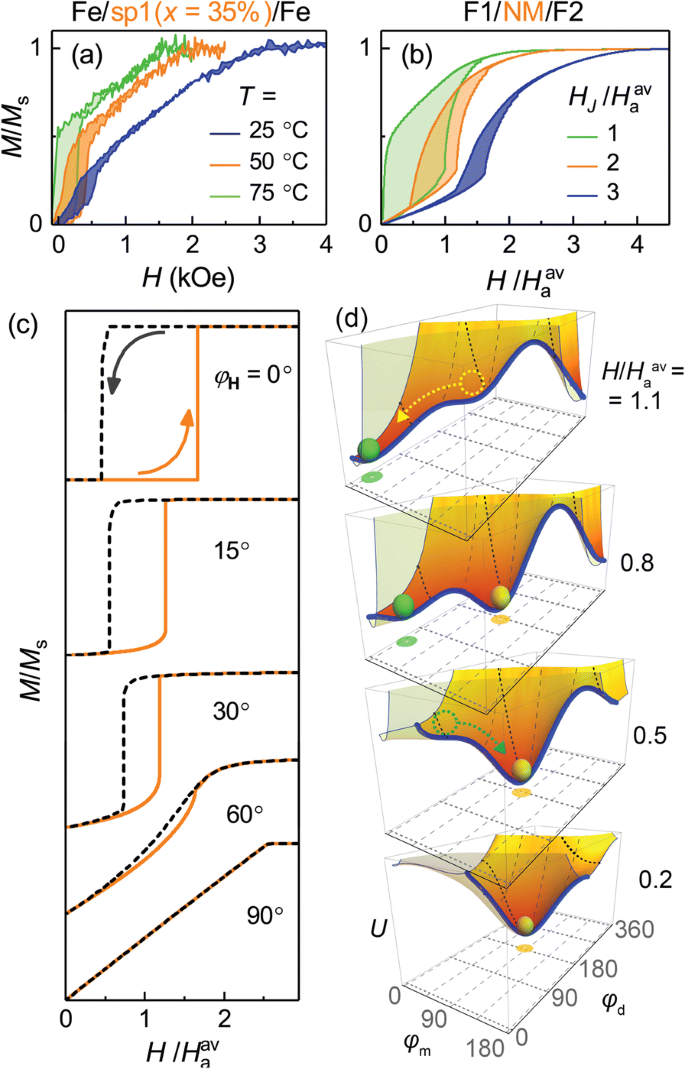
一 测量 M (H ) 系列样品的曲线，Fe/sp1(x =15%)/Fe，对于不同的温度。 b 对应的模拟M (H ) F1/NM/F2 三层模型在不同强度有效场 H 下的曲线 J 间接交换耦合。 (H ^av =(H a1 + H a2)/2，其中 H a1和H a2是层F1和F2的各向异性场。 c M (H ) 为选定角度模拟的曲线 φ H , 对于 H J /H ^av =2.d 自由能局部最小值的变换 (2) 作为外加场 H 的函数 , 对于情况 H J /H ^av =2 和 φ H =15°。蓝线描绘了连接不同 φ 能量最小值的路径 米 (φ d)。能量面的前表面是透明的，以方便说明

在单晶衬底上生长的外延 (100) Fe 基多层膜通常具有四倍面内磁各向异性 [12]，而其他纹理的衬底 [例如 (211)] 可导致双重各向异性 [11]。 M 的主要区别 (H ) 两种情况之间存在 M 中的两个特征步骤 对比 H 当各向异性是四倍并且只有一个 M -vs-H 步骤是双重的。我们对参考 Fe(2 nm) 薄膜和 Fe/Cr/Fe 三层（数据未显示）的 VSM 和 FMR 研究未显示磁滞回线或共振光谱中任何显着的平面内角度依赖性，使我们得出结论基本上不存在宏观面内磁各向异性。另一方面，上述数值分析得出的结论是，测得的阶梯形M (H ) RKKY 耦合的 Fe/Cr/Fe 三层的回路必须是由于形成多晶膜的单个微晶尺度上的双重磁各向异性。在我们的样品的情况下，薄膜平面中局部各向异性易轴的均匀角度分布可能是由于在旋转基板上的沉积造成的。然后可以根据溅射多层膜的多晶性质和纳米晶粒之间的面内应变变化来解释这种磁各向异性模式[18]。

M (H ) 模型系统 F1/NM/F2 的曲线，模拟不同强度的 AFM 层间交换耦合（有效场 H J ）并如图 3b 所示，展示了实验曲线中发现的所有关键特征（图 3a）。 M (H ) 对于 Fe/sp1(x =35 at.%)/Fe 随温度升高发生显着变化。变化是由于层间耦合减弱，可以直接对比模拟的M (H ）如图 3b 所示。在实验 M 中看到的所有变化 (H ) 数据，包括矫顽力随着层间耦合减弱而增强，与模拟行为非常相关，从而验证了模型。需要注意的是，模型计算没有直接考虑温度的影响（仅通过有效降低H J )，这应该会降低各个层的矫顽力。这可能是实验中矫顽力稍小的原因。

模拟的M (H ) 图 3b 所示的曲线是通过平均 M (H ) 计算不同角度 φ H 外场H之间 和单轴磁各向异性的易轴。图 3c 显示了选定角度 φ 处的曲线 H 对于H的情况 J /H ^av =2.这里，H ^av =(H a1 + H a2)/2，其中 H a1 和 H a2 是分别作用于 F1 和 F2 层的面内单轴各向异性的有效场。比率H a1/H a2 =0.7，用于计算，对应于实验获得的值（图 2b）。 φ 的阶梯状形状和矫顽力是明确定义的 H <60°。如上所述，参考 Fe(2 nm) 薄膜和 Fe/Cr/Fe 三层的额外 VSM 和 FMR 研究没有揭示任何显着的磁滞回线或共振光谱的平面内角度依赖性。由于 VSM 和 FMR 测量样品的积分特性，我们得出结论，基本上不存在宏观面内磁各向异性。另一方面，观察到的矫顽力只能归因于面内磁各向异性。此外，实验 M 的形状 (H ) 曲线更接近于通过平均获得的计算曲线而不是选择 φ 的任何单个曲线 H .因此，考虑到我们溅射多层膜的多晶性质，可以得出结论，Fe(2 nm) 层在膜平面中具有均匀的局部各向异性易轴的角度分布。

图 3d 说明了能量 U (φ 米，φ d) 等式。 2 响应 H 的变化 .我们再次取H J /H ^av =2 和 φ H =15°，对应于面板（c）中的第二条曲线。图 3d 中的粗实线描绘了连接不同 φ 能量最小值的路径 米 (φ d)。局部能量最小值在这个最小值路径中被明确定义。低场的最小值对应于 Fe 矩的反平行取向 (φ m ≈ 90°，φ d ≈ 180°）。随着H的增加 ，第二个局部能量最小值出现并加深，而第一个最小值变浅并最终消失。这种单极小状态对应于 Fe 矩的平行取向 (φ m ≈ φ H , φ d ≈ 0°）。在随后减小 H ，系统最初处于第二最小值（平行磁态），直到它在较低的 H 消失 并且系统最终处于第一个能量最小值（反平行状态）。

直接和间接交换耦合之间的竞争：矫顽力的温度依赖性

虽然第一个系列的三层 Fe/sp1/Fe 表现出从低温 AFM 层间耦合到高温解耦状态的热诱导转变，但第二个系列表现出从低温 FM 到高温 AFM 的转变耦合。对于第二种情况下的 FM 到 AFM 热转变，不需要外部磁场并且磁化切换是完全可逆的——这是应用的一个关键优势。

使用通过第一系列样品的上述分析验证的模型，我们接下来重点研究 Fe/sp2*(x )/Fe，具有 sp2* =Fex 类型的均匀间隔 Cr100 − x (1.5 nm) 和 sp2* =Cr(d Cr)/Fex Cr100 − x (d )/Cr(d Cr), d + d Cr =1.5 nm（sp2* 是从厚度固定的间隔物 sp2 =Cr(0.4)/Fex 的衍生物 Cr100 − x (0.7)/Cr(0.4) 的第二个系列）。图 4 比较了实验 M (H ) 具有 sp2 =Cr(0.4)/Fe15Cr85(0.7)/Cr(0.4) [面板 (a)] 和相应的 M 的结构的循环 (H ) 用 H 模拟的曲线 J 选择，例如获得最适合实验。首先要注意的是计算循环和测量循环之间的高度相似性，所有关键特征都被重现。其次，实验显示了从 FM 层间耦合 [图 4a 中的低温单回路] 到 AFM 耦合 [图 4a 中零剩磁的高温回路] 的温度诱导转变。各种有效耦合场值H的模拟回路形状的变化 J （图 4b）另外证实了所选择的现象学描述的有效性。与上一节相同，H a1/H 在模拟中使用 a2 =0.7。应该注意的是，即使这里不是这种情况，阶梯状的 M (H ) 形状是由于 AFM 层间耦合（例如，在 300 K 和 H J =0.5H ^av ) 原则上可以由 F1 和 F2 中不同的矫顽场在没有层间耦合的情况下引起 (H J =0)。然而，强 FM 层间耦合总是导致一个 M (H ) 循环。

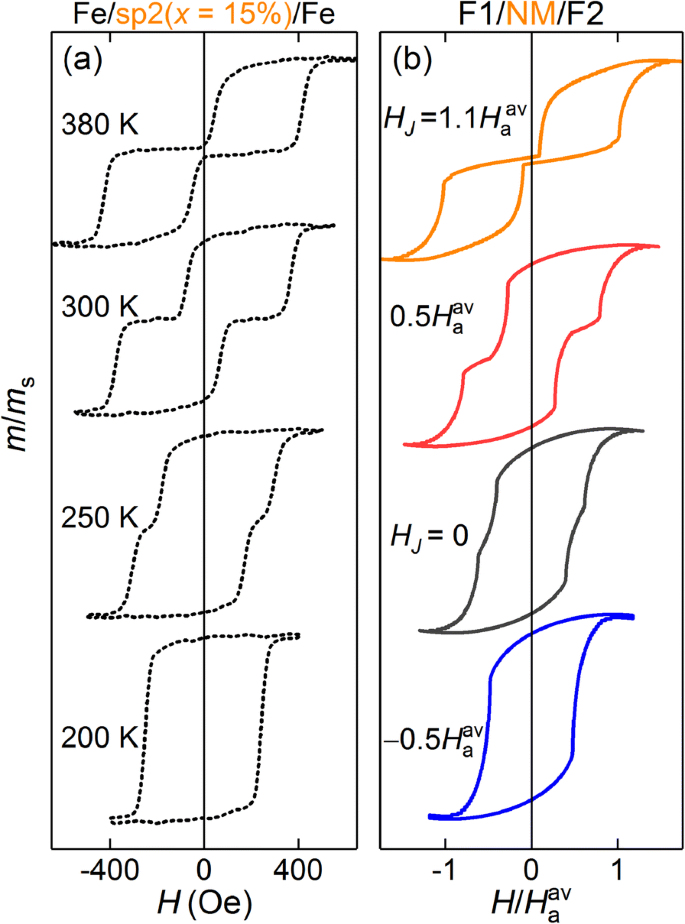
一 MOKE 测量的第二系列样品的磁化强度与磁场的关系，Fe/sp2(x =15%)/Fe，对于不同的温度。 b 对应的模拟M (H ) 模型 F1/NM/F2 三层的曲线，对于不同的间接交换耦合有效场，H J

部分环的矫顽力 (H c ^部分 ) 对所有样品都具有明显的温度依赖性，并且随着温度的降低几乎呈线性增加。图 5a 显示了矫顽场的温度依赖性，定义为磁化导数 dM 上两个峰值的场之间的差异 /dH 对比 H .带有 x 的系列 =15% 包含不同厚度的构成间隔层的样品：d (d Cr) =3 (6), 7 (4), 9 (3), 11 (2), 15 (0) Å。最后一个样本 [d (d Cr) =15 (0) Å] 是具有均匀间隔层 Fe15Cr85 (1.5 nm) 的三层。带有 d 的样本 ≤ 7 Å (d Cr ≥ 4 Å) 显示 H 单调增加 c ^部分 随着温度的降低。 d较小样品的矫顽力 Cr (<4 Å) 在刚好低于转变温度时开始偏离该斜率。 H的高温部分 c ^部分 (T )，然而，处于总体线性趋势 [在图 5a 中显示为粗红线]。矫顽力场与温度的这种线性斜率主要与外 Fe(2 nm) 层的本征矫顽力的变化有关。

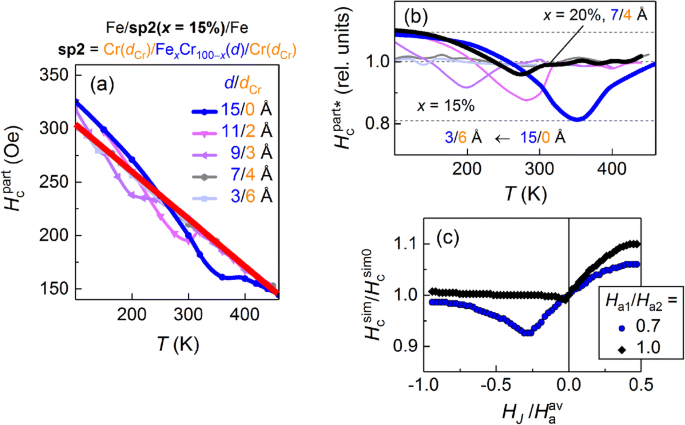
一 部分环矫顽力的温度依赖性 (H c ^部分 ) 对于结构 Fe/sp2(x =15%)/Fe 不同厚度的 Fex Cr100 − x 和 Cr 层 (d 和 d Cr，分别）在间隔 sp2。红色粗线是H高温部分的线性近似 c ^部分 (T ）。 b 矫顽力的温度依赖性归一化为线性背景。 c 矫顽力与H J 从模拟 M 获得 (H ) 两种情况的曲线： (1) H a1/H a2 =0.7 和 (2) H a1 =H a2

在我们之前的工作 [9] 中，间隔厚度为 d 的结构 ≤ 7 Å (d Cr ≥ 4 Å) 表现出最尖锐的热磁转换。然后我们提出磁跃迁变窄的原因是关闭了外 Fe 层之间的直接交换通道。另一方面，H的依赖 c ^部分* 对比 T （图 5b），通过归一化 H 获得 c ^部分 (T ) 到倾斜的内禀矫顽力背景，显示出明显的负 偏差仅适用于具有薄 Cr 间隔物的结构 (d Cr <4 Å) 并且对于 d 基本上没有偏差 Cr ≥ 4 Å。 x 的依赖 =20%, d Cr =4 Å 用于比较，因为 x 的转变 =15%, d Cr =4 Å (T C ^* ≈ 140 K) 接近最低测量温度。 H 上没有负偏差 c ^部分* 对比 T 对于带有 d 的结构 Cr ≥ 4 Å 可以作为直接层间耦合被完全抑制的额外确认。

对依赖H的部分进行分离分析 c ^部分 (T )，这是由层间耦合 (H J )，模拟的M的矫顽力 (H ) 与 H 作图 J 在图 5c 中。从而得到H c ^sim 对比 T 取决于 F1 和 F2 层的有效各向异性场之间的比率，H a1/H a2。 H的偏差越大 a1/H a2 来自 unity，最小值越深，其与图的 FM 侧零场的偏移越大 (H J <0)。当各向异性场相等时 (H a1/H a2 =1)，最小值不存在。这种行为类似于 H 之间的区别 c ^部分* (T ) 对于具有大 d 的均匀和复合垫片的结构 Cr (≥ 4 nm) [分别在图 5b 中的蓝色和黑色曲线]。这表明这两种类型的间隔物不同地传输两个外 Fe 层之间的层间耦合。在均匀间隔中，直接 FM 交换与间接 AFM 交换竞争，在某些温度下对其进行补偿，使得 H J =0。我们的模型很好地描述了这种情况，其中 F1 和 F2 层具有不同的各向异性场 [图 5c 中的蓝色曲线]。相比之下，复合垫片结构中的Fe层在低温下依次通过Fe/Cr/FeCr和FeCr/Cr/Fe进行FM耦合，垫片的FeCr内层处于FM状态。由于该 FeCr 层充当附加交换链接，间隔物以有效均衡外 Fe 层的矫顽力的方式传输交换 [图 5c 中的黑色曲线]。当 FeCr 层处于顺磁状态时，该系统的行为类似于具有均匀间隔层 [H 的高温部分的系统 c ^部分* 对比 T 图 5b 中的依赖关系和 H 的 AFM 侧 c ^sim 对比 T (H J> 0) 在图 5c]。

结论

总之，我们已经描述并比较了具有不同类型的层间交换介导间隔物的多层中温度诱导磁化转换的两种机制。切换机制反映了通过均匀间隔物的直接和间接交换耦合或通过复合间隔物的铁磁和反铁磁类型的全间接交换耦合的竞争。隔板设计的关键元素是弱磁性稀合金层，其居里跃迁转变为结构中的 P-AP 磁化转换。我们的测量数据得到了多层中磁滞的详细理论模拟的支持，解释为由于单轴磁各向异性的纳米颗粒，其易轴均匀分布在外铁磁层的平面中。对于不同的间隔件设计，磁过渡区中矫顽力的温度依赖性具有不同的形式。发现具有复合间隔物的结构的特定行为是抑制直接层间交换通道的结果，因此相关的 P-AP 切换机制是间接铁磁和间接反铁磁（均为 RKKY 型）交换的竞争。

因此，我们已经表明，间隔内直接层间交换的中断通道与更尖锐的热磁转变相关。我们还表明，纯间接层间交换、铁磁 RKKY 与反铁磁 RKKY 之间的热驱动竞争，其中垫片中的邻近效应不起作用，导致更好的开关性能。这些结果对于居里-RKKY 纳米结构在自旋热电子器件中的器件应用具有重要意义 [19, 20]。

缩写

原子力显微镜：

反铁磁性

AP：

反平行

调频：

铁磁性

FMR：

铁磁共振

IEC：

间接交换耦合

MOKE：

磁光克尔效应

NM：

无磁性

P:

平行

下午：

顺磁性

RKKY：

Ruderman-Kittel-Kasuya-Yosida

VSM：

振动样品磁力计