石墨烯加载超材料吸收器的耦合共振增强调制

背景

等离子超材料 (PM) 吸收器在深亚波长尺度上与金属纳米结构一起工作。可以在特定波长下实现和定制完美的吸收，从而实现各种应用，包括光发射器/检测器、传感器、光热疗法、光机相互作用和高光谱成像 [1,2,3,4,5,6,7 ]。 PM 吸收器还为设计具有可调特性的新型功能器件提供了一个有前途的平台。通过引入液晶、半导体或相变材料等组件，可以对光响应进行电、光或热调制 [8,9,10,11,12,13]，从而实现新型调制器、开关和多光谱探测器。

最近，石墨烯因其作为等离子体材料的高速调制能力和可调性而受到相当多的关注 [14,15,16,17,18,19,20]。具体来说，石墨烯的电导率取决于费米能级 (E F) 可以在几纳秒内通过偏置电压连续调谐，从而在近红外和中红外区域实现高调制率 [17, 19,20,21,22,23,24]。然而，由于单个石墨烯层只有原子级厚，入射光和等离子体共振之间的相互作用非常弱。由于带间跃迁的泡利阻塞，这种相互作用在中红外区域变得更加微弱 [22]。因此，波长调谐范围和调制深度非常有限。波长漂移一般小于共振波长的 10% [21, 22, 25,26,27,28]，这对于光通信和宽带光谱检测的实际应用仍然是一个挑战。因此，为了实现高效的电光调制，需要大大加强石墨烯与光的相互作用。前人的研究取得了一些进展。基于纳米天线和裂环谐振器等复杂纳米结构的设计 [19, 21, 22, 25, 27, 28]，石墨烯-光相互作用的增强已在理论上和实验上得到证明。然而，这些设计通常复杂或依赖极化，工作频率范围较小，可调性仍然有限。

在这项工作中，我们提出了一种调制范围为 9 到 14 μm 的石墨烯负载吸收器，这对生物化学传感和热成像等应用非常感兴趣 [5, 29,30,31]。十字形槽内的耦合共振为电场提供了四个数量级的增强，强烈加强了石墨烯与光的相互作用，并导致中心波长的偏移高达 25%。此外，我们提出了一个简单的 LC 电路模型，它很好地解释和预测了由电压和几何参数控制的石墨烯诱导调制。如此大范围的可调性将在许多应用中大有可为。

方法

如图1a所示，图案化的金属贴片以Λ =8 μm的周期排列在由介电间隔物隔开的金属基板上。单层石墨烯夹在贴片和垫片之间。基板很厚，起到反射镜的作用。间隔层的厚度为t d =520 nm，金属贴片为t m =100 nm。图 1b 显示了一个单元电池的俯视图。两个子单元以对角线对称的方式排列，以支持极化无关性。每个方形贴片上蚀刻一个十字形槽，将其分成四个相同的小块。 S 中小同种的大小 1 和 S 2 个是 l 1 =1.5 μm 和 l 分别为2 =1.7 μm。两个子单元的槽宽度为 a =20 nm。在我们的研究中，金属材料被选择为金 (Au)，其光学性质由 \( \varepsilon \left(\omega \right)=1-{\omega}_p^2/\left 的 Drude 模型描述(\omega \left(\omega +\tau \right)\right) \) 与 ω p =1.369 × 10 ¹⁶ 赫兹和τ =1.224 × 10 ¹⁴ 赫兹 [32]。介电间隔物由硫化锌（ZnS）组成，其光学指数为n =2.2，在中红外区域的损失可以忽略不计[33]。

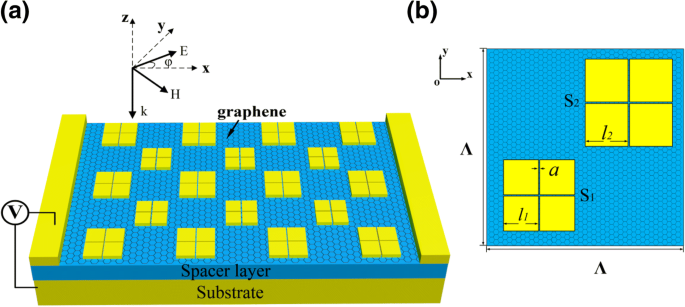
一 所提出的石墨烯负载超材料的示意图。每个亚单元中的十字形槽可以极大地增强石墨烯与光的相互作用，而不会产生偏振依赖性。 b 在一个时期内的结构顶视图。两个亚基对角排列，斑块大小不同

有限差分时域（FDTD；Lumerical FDTD Solutions）方法用于计算反射光谱和电磁场分布。模拟是在 x 的周期性边界条件下进行的 和 y z 中的方向和完美匹配层条件 方向。通过表面电导率方法将单个石墨烯层建模为二维结构 [34]。石墨烯层的表面电导率σ g，包括带间项σ 间和带内项σ 内，可由久保公式计算[35]。

其中 e 和 ξ 是电子的电荷和能量，ℏ 是简化的平板常数，ω 是角频率，\( {f}_d\equiv 1/\left({e}^{\left(\xi -{E}_F\right)/{k}_BT}+1\right) \) 是指到费米-狄拉克分布，T 是绝对温度，Γ 是散射率，k B 是玻尔兹曼常数，E F 是费米能级。在我们的计算中，T =300 K，且Γ =10 meV [28]。石墨烯层附近的网格尺寸为 0.25 nm，槽中的网格尺寸为 2.5 nm。石墨烯的有效介电常数可以表示为

其中 ε 0 是真空的介电常数，t g 是石墨烯层的厚度。方程（1）和（2）表明石墨烯的光学常数随E而变化 F. 这种变化导致吸收频率的可调性，通过纳米结构中的耦合共振可以大大扩大吸收频率的范围，从而大大降低器件的施加电压。

结果与讨论

图 2a 显示了 x 的吸收光谱 -极化波（φ =0) 在正常发生率。当费米能级为 E F =0eV，在波长λ处观察到两个吸收峰 =12.4 μm 和 13.3 μm，分别。范围从 12.1 到 13.5 μm 的入射光几乎被纳米结构吸收。作为 E F 增加，共振向更短的波长移动。在 E F =0.2 eV，吸收峰移至11.8 μm和12.46 μm，相对位移分别为4.8%和6%。同时，峰值 2 的吸光度下降，这是由于在较高的 E 下超材料和空气之间的阻抗不匹配 F [28]。有趣的是，随着费米能级的不断增加，峰 2 的蓝移速度比峰 1 快。稍后将通过电路模型来解释这种观察到的行为。

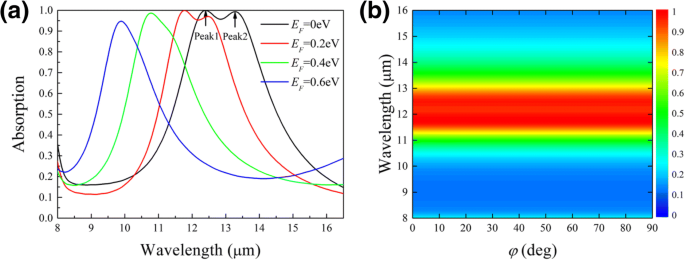
不同E在法向入射处的吸收光谱 F 在 φ =0，随着 E 的增加，峰的蓝移很大 F (a )，以及不同的 φ 在 E F =0.2eV，证明了极化无关性 (b ）。偏振角φ 定义如图 1a

调制可以通过参数M来量化 =Δλ /λ 0，其中λ 0 是 E 处的共振波长 F =0 eV和Δλ 是由于 E 的变化引起的波长偏移 F. 图 2a 显示了 M 1 =20.1% 和 M 当 E 时，峰 1 和峰 2 分别为 2 =25.5% F 达到 0.6 eV。与以前的工作相比，共振的调制范围要宽得多 [19, 21, 22, 25,26,27,28]。如此大的调制在低 E 对于许多应用，F 是非常理想的。单独的计算表明，随着间隔物厚度的减小，吸收峰蓝移（附加文件 1）。因此，我们可以优化厚度以设置合适的调制起始点。此外，所提出的超材料的光学响应与偏振无关，如图 2b 所示。当偏振角φ时吸收光谱保持不变 由于设计的对称性，从0°到90°不等。

共振的场分布清楚地说明了完美吸收的机制。由于众所周知的金属-绝缘体-金属 (MIM) 结构 [3, 32, 36,37,38] 如图 1 所示，局部 SPP 被刺激以在每个贴片中形成紧凑的磁共振。图 3a 和 b 展示了归一化磁场 |H| ² 在 E 的石墨烯层中 F =0.2 eV，在λ的共振波长下 1 =11.8 μm和λ 分别为2 =12.46 μm。由于 SPP 具有很强的局部性，因此两个子单元可以独立工作。然而，由于每个子单元内部分裂槽的宽度很窄，四个相同的共振实际上是相互耦合的。并且这种耦合极大地增加了槽内的电场，如图 3c 和 d 所示。只有 E y 中的字段 -方向槽在这里很明显，因为入射光在 x 极化。 E 的强度 共振耦合增强的场比入射光的场强四个数量级E 公司相比之下，先前工作中用于调制的最强化场位于补丁边缘。图 3e 和 f 分别显示了沿图 3c 和 d 中白线的槽和边缘之间增强的鲜明对比。

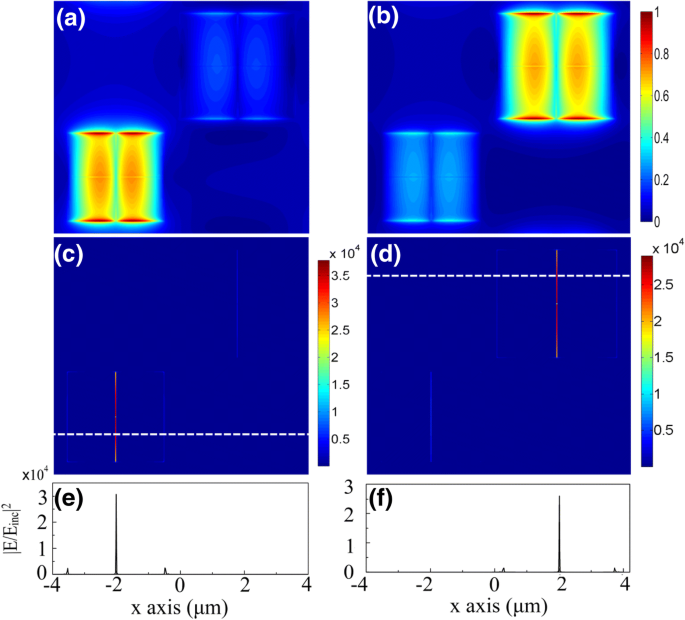
E 石墨烯层中的场分布 F =0.2 eV 对于法向入射的 x 偏振光，显示耦合共振引起的缝隙中的极大增强。 a, b 归一化磁场|H| ² 在 λ 1 =11.8 μm (a ) 和 λ 2 =12.46 μm (b ); c , d |E/Einc| ² 对应的场分布; e , f |E/Einc| ² 沿着 c 中显示的白色虚线 和 d ， 分别。插槽内部的强度与补丁边缘的强度之间形成鲜明对比，提示比以前的作品更宽的调谐范围

这种场分布很好地解释了为什么在我们的提议中调制如此之大的原因。基于微扰理论，石墨烯引起的共振位移可以评估为 Δω =− iσ g ∫S |Es| ² dS /W 0 [22]。这里，|Es| ² 是石墨烯层中的电场强度，W 0 是储存的能量，S 表示被石墨烯覆盖的区域。共振的谱位移 (Re(Δω )) 由 σ 的虚部决定 g，远大于其在中红外区域的实部 [22, 28]。如图 3c-f 所示，窄槽内的电场增强是边缘的 10 倍以上。因此，积分值主要由大大增强的 E 贡献 补丁槽中的场，导致峰值的偏移比以前仅具有增强的 E 的情况大得多 金属边缘的场 [21, 22, 25, 27, 28]。

根据场分布和上述讨论，提出了一个 LC 电路模型来研究调谐行为。如图4a所示，L 我 和 C 我 (i =1, 2) 分别是贴片S的电感和电容 我 在图 1b 中。当槽宽a 非常大而且没有石墨烯层，我们可以忽略槽和石墨烯引起的影响。然后，L 我 和 C 我 可以通过与吸收光谱中获得的共振波长进行拟合，通过单独计算来确定 [37, 39, 40]。结果是L 1 =0.07 pH值和C 对于亚基S，1 =350 aF 1、同时L 2 =0.075 pH和C 对于亚基S，2 =380 aF 2. 每个子单元内部的槽感应耦合效应可以用并联电容C来描述 c ，发现随着槽宽度a的增加而减小 .在我们的例子中，C c 对于 a 是 290 aF =20 nm，并且 a 每增加 10 nm，变为 200 aF、180 aF 和 135 aF .谐振波长是通过让电路的阻抗为零得到的，即\( {\lambda}_i^0=2\pi {c}_0\sqrt{L_i{\mathrm{C}}_i^0} \)。在这里，c 0 是真空中的光速，“i ” 指亚基S 我 , 和 \( {C}_i^0={C}_i+{C}_c \).

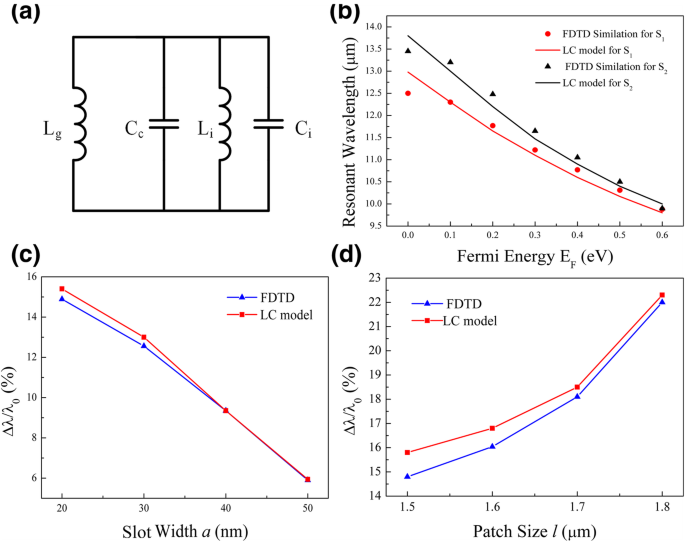
一 LC 电路模型包括来自不同贴片 (L 我 和 C 我 ), 槽 (C c ) 和石墨烯 (L g ）。 b LC 模型计算的共振与 FDTD 模拟相比。 c , d E 处单个贴片的共振位移 F =0.4 eV 随着 c 的几何参数的变化 槽宽 (l =1.5 μm) 和 d 补丁大小 (a =20 nm)

二维石墨烯层基本上充当电感器。如图3所示，石墨烯层的主要贡献来自电场增强的槽位。由于狭缝宽度远小于工作波长和石墨烯等离子体的波长，准静态近似是有效的。电压V 和当前的 I 可以通过 V 评估整个插槽 =aE 和我 =2l 我t g(σ g − iωε 0)E , 其中 E 是石墨烯层中的电场。所以，我们可以引入一个电感 L g =− 1/ω Im(V/I) [41]，描述了石墨烯层的贡献，发现是

该电感器用作图 4a 中所示的并联元件。因此，一个贴片的总电感为\( 1/{L}_i^{\prime }=1/{L}_i+1/{L}_{\mathrm{g}} \)。每个亚基的最终共振波长，与石墨烯层，变为

由于每个子单元独立工作，因此可以将两个子单元的阻抗并联得到超材料的总阻抗。

该 LC 模型预测随着 E 的增加，共振会发生蓝移 F. 从方程推导出来。 （1）和（2），我们得到了更大的|Re(ε g)|对于较高 E 的石墨烯 F，它给出了一个更小的 L 方程中的 g (3).由于电感并联，最终电感 \( {L}_i^{\prime } \) 变得更小，导致等式中的谐振波长更短。 (4).计算结果总结在图 4b 中，显示与 FDTD 模拟获得的谐振波长非常吻合。看到小偏差是因为我们的 LC 模型忽略了每个补丁边缘弱场的贡献（图 3c-f）。 LC 模型还显示了几何参数如何影响共振的蓝移。微分方程(4)，我们有\( \partial {\lambda}_i^{\prime }/\partial {L}_i^{\prime}\propto 1/\sqrt{L_i^{\prime }} \)。很明显，\( \sqrt{L_i^{\prime }} \) 的小值有利于增加这种蓝移的灵敏度。因为电感是并联的，L 我 是固定的，总电感值 \( {L}_i^{\prime } \) 的小值意味着石墨烯电感 L 的小值 G。为了增加调谐范围，槽宽a 应该很小，补丁大小 l 大，根据方程。 (3).图 4c 显示了 E 处的共振蓝移 F =0.4 eV 从大约 6% 增加到 15%，当 S 内的槽宽度 1 从 50 减少到 20 nm。另一方面，如果我们将槽宽度固定在 a =20 nm，共振从 15% 增加到 22%，贴片尺寸从 1.5 变为 1.8 μm，如图 4d 所示。与FDTD模拟的良好一致性表明，这种简单的电路模型是研究相关超材料器件的有效方法。

结论

总之，我们设计了一种具有大范围调制的与偏振无关的宽带超材料吸收器。对于两种谐振，当 E 时，调谐范围可达中心波长的 20.1% 和 25.5% F 从 0 增加到 0.6 eV。如此大的调制来自石墨烯-光相互作用，通过每个金属贴片的十字形槽内的耦合共振大大增强。这种效应在 LC 模型中由石墨烯引入的电感器很好地描述。这样一个简单的模型预测了不同几何参数下的调制行为，结果与 FDTD 模拟非常吻合。我们的提议有利于光通信、传感和热成像等潜在应用。

缩写

E F ：

费米能级

FDTD：

有限差分时域

MIM：

金属-绝缘体-金属

下午：

等离子超材料

ZnS：

硫化锌