大面积外在手性金属纳米新月阵列的巨大可调圆二色性

介绍

如果一个物体的结构不同于它的镜像对映异构体 [1]，那么它就是手性的。手性是各种化合物（例如生物和化学物质或人造超材料）所具有的普遍特性[2]。这种结构特性广泛应用于物理学、生物学、化学和医学等许多领域[3,4,5,6]。手性贵金属纳米结构在过去的几十年中得到了广泛的研究，因为它们具有可调的光学特性，包括旋光性、圆偏振光的不对称传输和非凡的圆二色性 (CD) [7,8,9,10,11 ,12,13,14]。这些特殊的特性归因于这些结构的强光学响应，它是由局部表面等离子体共振 (LSPR) 产生的。这种现象对金属纳米结构的形状、尺寸和周围环境很敏感 [15,16,17]。由于这些原因，手性金属纳米结构可用于许多应用，例如负折射 [18,19,20]、光源偏振的操纵 [21,22,23] 和手性分子传感 [ 24, 25]。

通过倾斜照明破坏实验装置的镜面对称，也可以在非手性超材料中产生光学手性。由于缺乏化合物的双重旋转对称性，这种现象被称为“外在手性”。外在手性最初由 Bunn 于 1945 年引入并证明。Zheludev 及其同事在金属开口环中发现了外在手性引起的外在手性响应。此外，他们研究了这些结构的电偶极子和磁偶极子之间的相互作用机制 [26, 27]。最近，Leon 等人。 [28] 在实验和理论上证明了由金属裂环阵列组成的超表面中的大圆二色性。与手性金属纳米结构相比，具有大表面的外在手性金属纳米结构更容易制造 [29,30,31,32,33,34]。此外，它们显示出更强的手性光学特性，例如 CD，这意味着该化合物在与左圆偏振 (LCP) 或右圆偏振 (RCP) 入射波相互作用时呈现不同的透射率 [35, 36]。在同一研究小组之前的工作中，制造了大面积随机分布的金属新月形纳米结构，并证明它具有大的光学手性 [37]。然而，由于随机分布的纳米新月体密度低，实验中获得的CD系数低于预期。此外，随机分布的金属新月形纳米结构的均匀性存在一些缺陷，这阻碍了该化合物在应用中的使用。由于阵列结构提供了大的单元密度和良好的均匀性。开发简单、知名且低成本的制备方法来生产大面积、均匀、外在的手性金属阵列结构，对促进金属手性在应用中的应用提出了新的挑战。

在这项工作中，使用聚苯乙烯 (PS) 微球阵列作为模板制造了晶格常数在 500-1000 nm 范围内的金属新月形纳米结构的周期性阵列。 CD 的最大值 (0.51) 在 1270 nm 处测量，晶格常数为 800 nm。对所提出的结构进行了模拟，发现与实验测量结果非常吻合。根据模拟，这种强烈 CD 效应的主要机制是通过圆偏振光选择性激发 LSM。此外，通过改变结构的晶格常数，通过实验验证了 CD 效应的可调性。由于 PS 微球是市售的，金属新月形纳米结构周期性阵列的外在手性可以在很宽的光谱范围内进行调制，该范围从可见光到红外区。所提出的样品具有二色性高、易于制作和标准制作技术兼容等优点，有望在圆偏振光成像和传感方面得到应用。

方法

以不同尺寸的PS纳米球为模板，制备了具有不同晶格常数的金属新月形纳米结构的大面积等边三角形晶格阵列。本工作中使用的 PS 纳米球的直径为 500、650、800、850 和 1000 nm。制造过程如图1a所示。最初，通过自组装过程在预处理的石英表面上形成单层六边形密堆积 PS 球阵列 [38]。然后通过形成氩等离子体 6 分钟 (PDC-32G-2) 来蚀刻密堆积的胶体单层，以获得非密堆积的模板 [39, 40]。样品保持在 0.2 毫巴的压力下，光的输入功率设置为 100 毫瓦。随后，通过倾斜角为 45° 的离子束溅射涂层沉积 50 nm 薄金层。金膜被离子束垂直蚀刻。最后，使用丙酮去除纳米球模板，形成金属新月形纳米结构的大面积等边三角形晶格阵列。根据基本的几何考虑，可以通过选择不同直径的 PS 纳米球来调整新月直径。此外，通过控制沉积在样品上的金量和最大月牙宽度w，可以直接获得薄膜厚度 金属的表示为

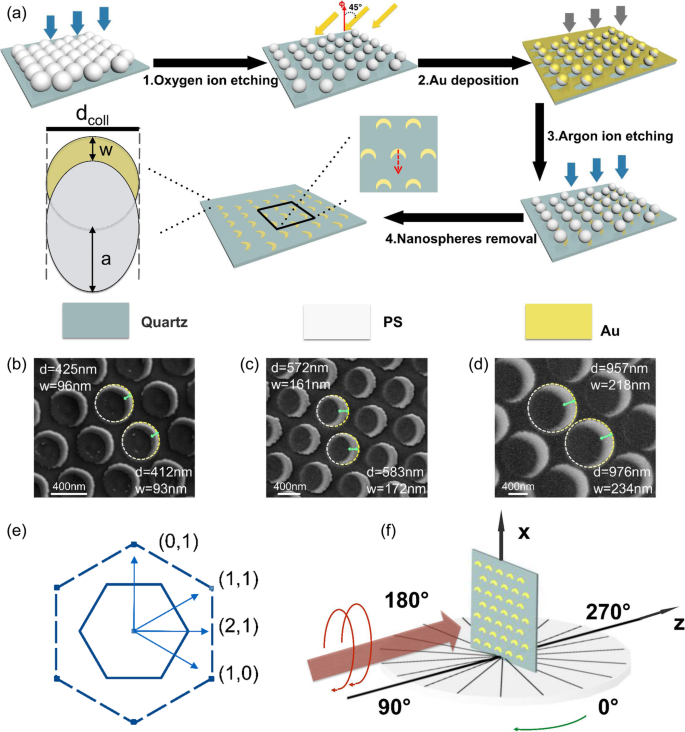
一 新月形制备过程示意图和指示直径 d 的颗粒几何形状 掩蔽胶体coll和最大新月宽度w 的金属。红色箭头表示纳米新月镜轴的正方向； b –d 具有晶格常数的结构的SEM图像：b 500 纳米，c 800 纳米，d 1000 纳米。绿色箭头的长度代表月牙形结构w的最大宽度 .虚线表示与圆拟合后的新月形结构的直径（蚀刻的PS纳米球）； e 倒易格由基向量 (1, 0) 和 (0, 1) 构成。显示了倒数向量 (1, 1) 和 (2, 1)。倒格图中的连续和虚线分别代表第一和第二布里渊区的边界。 f 实验方案设计

代入Φ =45°，在此处讨论的整个研究中使用，在上述等式中产生

必须注意的是，实际上，与图 1a 中建议的理想化几何形状会发生偏差。 w ，在扫描电子图像中看到，图 2b-d，比理想情况略小。作为额外的系统不确定性，应考虑胶体的蚀刻和聚集。图1a中的红色箭头定义了纳米新月的镜轴正方向，即朝向纳米新月的开口方向。如图1b-d所示，纳米新月体的镜轴方向是一致的，这可以通过倾斜沉积过程确定并人工控制。金属纳米新月体规则地排列在相对较大的区域内。然而，由于制造缺陷，在测量几平方毫米的光学测量区域之外难以控制晶格的取向。因此，金属纳米新月的方向与等边三角形晶格的相对取向是随机的。

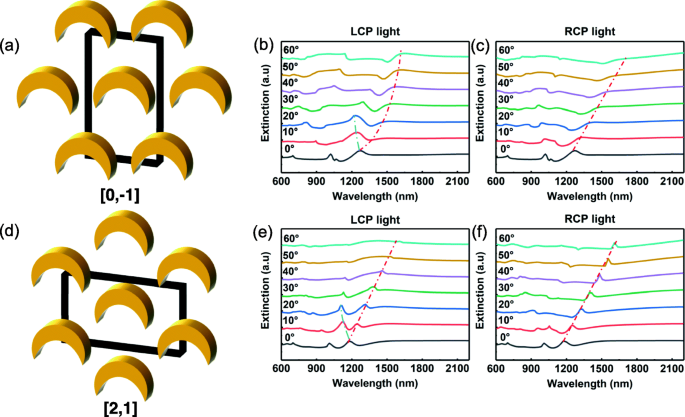
一 , d 纳米新月的镜轴分别朝向 [0, - 1] 和 [2, 1] 晶轴的晶格示意图（方块代表晶胞）； b , c 通过分别使用具有左圆偏振和右圆偏振的入射光记录的消光光谱。纳米新月的镜轴指向晶格的[0, - 1]方向； e , f 通过分别使用具有左圆偏振和右圆偏振的入射光记录的消光光谱。纳米新月的镜轴指向晶格的[2, 1]方向

使用基于有限差分时域 (FDTD) 方法的麦克斯韦方程求解器对具有外在手性响应的样品进行建模。选择晶格常数为 800 nm 的金属纳米新月阵列结构（即由直径为 800 nm 的 PS 微球形成的样品）进行模拟。虽然在实验中纳米新月的镜轴与晶格之间的相对取向是随机的，但在模拟中，纳米新月的镜轴选择朝向[0, - 1]和[2, 1]晶轴，如图所示为简单起见，图 2a、d。在这里，石英构成基板，Au 是金属，如 Johnson 和 Christy 模型所示。沿 x 应用周期性边界条件 - 和 y - 方向。 FDTD 网格尺寸设置为 2 nm，以提供等离子体效应的准确计算。通过将左旋圆偏振光和右旋圆偏振光照射到样品上，同时围绕金属纳米新月体的旋转对称轴旋转样品，可以改变入射角，如图1e所示。

结果与讨论

二维纳米颗粒阵列中的表面晶格共振 (SLR) 已得到广泛研究。光谱中的消光特征是由晶格表面模式 (LSM) 产生的，它是由掠过衍射级或瑞利异常 (RA) 产生的 [28, 41]。在这项工作中，纳米粒子的尺寸由晶格常数近似。因此，尽管通过添加石英基板引入了环境折射率不对称性，但仍然可以观察到由 LSM 引起的光谱中存在的消光特征 [42]。此外，由于 LSPR 与相邻金属粒子的强耦合，可以观察到源自瑞利异常条件的显着红移 [43]。这些现象将在本工作的以下部分详细介绍。

当纳米新月的镜轴指向[0, - 1]晶格晶轴且光的入射角为0°时，两种圆偏振光产生的消光光谱重叠。此外，每个光谱表现出三个消光峰，分别位于 697 nm、1019 nm 和 1265 nm（图 2b、c）。由于位于 697 nm 处的消光峰强度低且对 CD 效应的贡献很小，因此没有对该特征进行进一步研究。位于 1265 nm 处的消光峰主要由 LSMs (± 1, 0), (1, 1) 和 (− 1, − 1) 引起，而出现在 1019 nm 处的特征主要由 LSMs (2 , 1) 和 (− 2, − 1)。新月结构的引入消除了简并性，因为它的特点是对称度相对较低。因此，当它被入射角为 0° 的光照射时，1019 nm 处的消光峰会分裂。当入射角θ 增大且镜轴平行于晶格的[0, − 1]方向，LSMs的共振方程可写为：

\( {\lambda}_{RA}^{\pm}\left(\theta \right)=\frac{\sqrt{3}}{2}\varLambda n\left[1\pm \frac{\sqrt {3}}{2}\sin \left(\theta \right)\right] \) 用于 (±1, 0)、(1, 1) 和 (−1, −1) 模式；

\( {\lambda}_{RA}^{\pm}\left(\theta \right)=\frac{1}{2}\varLambda n\left[1\pm \sin \left(\theta \right )\right] \) 用于 (2, 1), (−2, −1) 模式。其中Λ 是等边三角形晶格的晶格常数，测量值为 800 nm；符号 ±（正或负）取决于 LSM 的第一个数字； n 是等边三角形晶格周围的有效折射率，对于每个 LSM，它假定几乎相同的值 (1.25)。通过在上面的表达式中引入这些值，LSMs (± 1, 0), (1, 1) 和 (− 1, − 1) 引起的消光峰应该出现在 866 nm，而 LSMs 引起的特征(2, 1) 和 (− 2, − 1) 在 500 nm。然而，模拟结果表明这些峰位于 1265 nm 和 1019 nm，这意味着它们与计算的峰有很大的红移。红移是由 LSPR 模式与相邻金属纳米粒子的强耦合引起的 [43]。 LSPR 模式与相邻金属纳米新月体的耦合强度对于不同的几何配置和模式是不同的，这会导致它们的光学响应发生红移。在这项工作中，红移的不同值取决于有效折射率，n , 在共振方程中。纳米新月体镜轴朝向[0, − 1]晶轴和θ时测得的有效折射率 =0°对于 LSM (± 1, 0)、(1, 1) 和 (− 1, − 1) 为 1.46，对于 LSM (2, 1) 和 (− 2, − 1) 为 2.04。随着入射角的增加，简并性被消除，1265 nm 和 1019 nm 处的消光峰变得更宽或分裂。 LSPR模式的激发效率随着θ的增加而有不同的变化趋势，消除简并性是一个非常复杂的过程。 .因此，这项工作集中在产生巨大CD效应的主要因素上。如图 2b、c 所示，随着 LCP 光入射角的增加，位于 1265 nm 的消光峰发生蓝移，但在使用 RCP 光的消光光谱中未观察到这种现象。这些结果表明用 RCP 和 LCP 入射光测量的消光光谱之间存在显着差异，这可能与测量的巨大 CD 效应有关；虽然 LCP 光可以激发 (− 1, 0) 和 (− 1, − 1) LSM，但 RCP 光不会发生这种情况。

当纳米新月的镜轴与晶格的 [2, 1] 轴对齐时，可以获得类似的结果。如图2e，f，当θ =0°，两种圆偏振入射光的消光光谱重叠。此外，每个光谱还表现出三个消光峰，分别位于 697 nm、1019 nm 和 1171 nm。以下分析不考虑位于 697 nm 处的消光峰。观察结果表明，位于 1171 nm 的消光峰主要由 LSMs (0, ± 1) 引起，而位于 1019 nm 的消光峰可能由 LSMs (- 1, 1), (1, - 1) 产生, (1, 2) 和 (− 1, − 2)。随着入射角的增加，θ ，当镜轴平行于晶格[2, 1]方向时，LSMs的共振方程可写为：

\( {\lambda}_{RA}^{\pm}\left(\theta \right)=\frac{\sqrt{3}}{2}\varLambda n\left[1\pm \sin \left( \theta \right)\right] \) 对于 (0, ±1) 模式；

\( {\lambda}_{RA}^{\pm}\left(\theta \right)=\frac{1}{2}\varLambda n\left[1\pm \frac{\sqrt{3}} {2}\sin \left(\theta \right)\right] \) 用于 (−1, -1)、(1, −1)、(1, 2) 和 (−1, −2) 模式。

符号 ±（正或负）取决于 LSM 的第二个数字。当 θ =0°, n LSM (0, ± 1) 的值为 1.35，而 LSM (− 1, 1)、(1, − 1)、(1, 2) 和 (− 1, − 2) 的测量值为 2.04。当入射角增加时，1171 nm 和 1019 nm 处的消光峰变宽或分裂。类似地，当纳米新月的镜轴平行于 [0, - 1] 晶轴时，使用 RCP 和 LCP 入射光记录的消光光谱之间最显着的差异是一系列消光峰。与位于 1171 nm 处的峰相比，它们发生蓝移。此外，随着入射角的增加，它们仅出现在通过 LCP 入射光测量的消光光谱中，但如果使用 RCP 光则无法观察到。这一观察结果可以解释测量到的巨大 CD 效应，因为只有 LCP 光可以激发 (0, - 1) LSM。通过左右圆偏振光对 LSM 的选择性激发可能是在外在手性阵列结构中观察到的巨大 CD 效应的原因，这种观察结果与参考文献一致。 [28].

进行实验测量以获得样品的消光光谱和CD光谱。开发了由紫外-可见-近红外分光光度计组成的测量系统。光通过格兰-泰勒棱镜和广谱四分之一波片驱动，以确保可以实现圆偏振并在一定角度下照射样品。这个角度可以通过旋转样品台来精确控制。 CD 系数可以使用以下公式计算：

其中 L 分机 和 R 分机 分别是用分光光度计通过 LCP 光和 RCP 光测量的金属纳米新月体的消光强度。结果显示在图 3d、e 中，而 CD 光谱显示在图 3f 中。为了使模拟接近实验条件，将两种配置的消光光谱叠加（图 3a、b）并计算模拟 CD 系数（图 3c）。模拟与实验结果非常吻合，尤其是在 CD 光谱的情况下。如图3d，e，当θ =0°，LCP 和 RCP 入射光测量的消光光谱几乎相同。此外，存在位于 696 nm 和 1838 nm 的两个显着消光峰。结果表明，696 nm 处的消光峰是由高阶 LSPR 模式产生的。由于 LSM (± 1, 0), (1, 1), (− 1,− 1), (0, ± 1) 和 LSPR 偶极子模式，1838 nm 处的消光峰可能会出现。随着θ的增加 ，696 nm 处的消光峰最初减小然后再次增加，尽管其强度在 LCP 和 RCP 光谱中不同。这一观察结果与本课题组前期工作的结论一致。 1838 nm处的消光峰变化不大，随着θ的增加，在1390 nm处出现了新的消光峰 当使用 LCP 入射光时。这导致 (− 1, 0)、(− 1, − 1) 和 (0, − 1) LSM 的激发。当样品通过RCP入射光激发时，1838 nm处的消光峰红移，强度随着θ而减弱 增加。虽然在 1390 nm 处没有消光峰，但当 θ 时在 1080 nm 处出现了一个新特征 增加，这可能是由 LSPR 模式产生的。如图3f所示，随着θ的增加 ，出现一个主要的 CD 峰并发生红移。当 θ =30°，可在 1270 nm 处测量 CD 系数的最大值 (0.51)。 (− 1, 0)、(− 1, − 1) 和 (0, − 1) LSM 通过圆偏振光的选择性激发触发了导致巨大 CD 效应的机制。由于生产过程中的缺陷，实验得到的消光峰和CD峰比模拟峰稍宽。

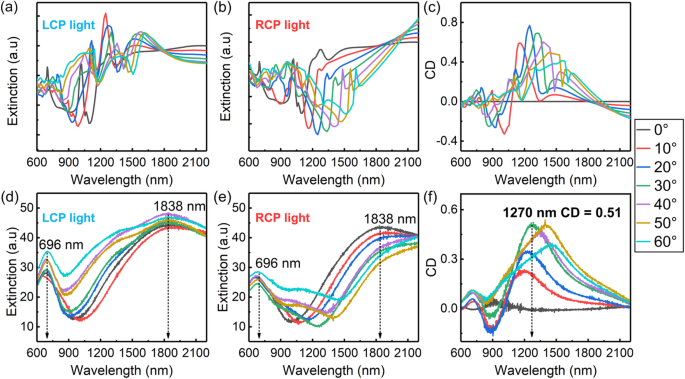
模拟和测量的消光和 CD 光谱。 一 –c 圆偏振光不同入射角的模拟加性消光光谱：a LCP，b RCP 和 CD 光谱。 d –f 不同入射角圆偏振光的测量消光光谱：d LCP，e RCP和CD光谱

此外，这项工作表明，可以通过调整 PS 微球的直径来调整金属新月形纳米结构阵列的外在手性。图 4 显示了在 500-1000 nm 范围内具有 θ 的不同晶格常数（即 PS 纳米球的直径）的几种金属纳米新月阵列的 CD 光谱 =30°。随着晶格常数的增加，CD光谱的峰值从1019nm红移到1799nm，CD系数保持较大（>0.25）。由于直径在 50 nm 和 10 μm 之间的 PS 微球可以在商业上获得，因此可以调节结构的外在手性，以用于其在从可见光到红外的广泛波长范围内的应用。

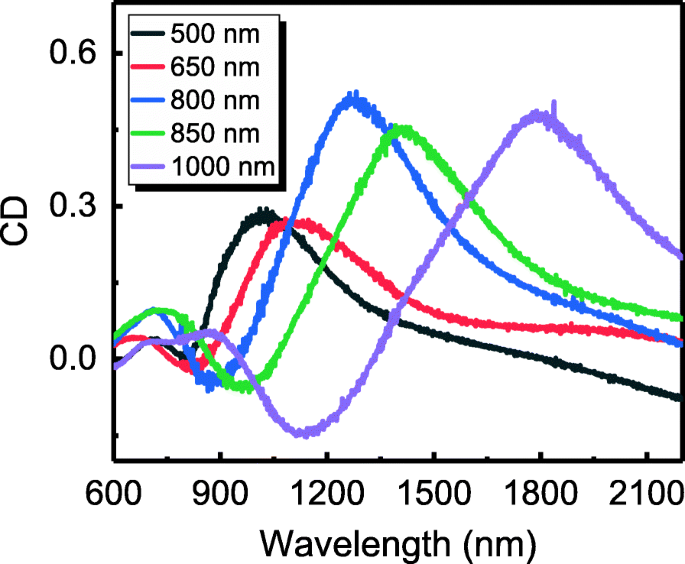
直径在500-1000 nm范围内的金属纳米新月阵列的CD光谱；光源入射角为30°

结论

总之，我们已经证明大面积金属纳米新月阵列结构显示出相当大的外在手性效应，以及高模块化和简单的制造方法。成功制备了具有不同晶格参数的样品，并从理论上和实验上研究了 CD 效应。最大 CD 系数 (> 0.5) 是在 1270 nm 处使用 30° 入射角在金属新月形阵列中以 800 nm 周期测量的。此外，通过改变 PS 微球的直径，可以广泛地调整这种结构的 CD 光谱，同时保持大的峰值强度。当晶格常数在 500-1000 nm 范围内变化时，CD 峰的位置从 1019 到 1799 nm 不等。模拟与实验结果非常吻合，样品的大且可调的外在手性效应可归因于 LCP 和 RCP 诱导的 LSM 的选择性激发。所展示的结构可用于遥感和偏振成像。

数据和材料的可用性

本研究期间生成或分析的所有数据均包含在这篇已发表的文章中。

缩写

LCP：

左圆偏振

RCP：

右圆偏振

CD：

圆二色性

LSPR：

局域表面等离子体共振

LSMS：

晶格表面模式

SLRS：

表面晶格共振

SEM：

扫描电子显微镜