MBi 和 MSb（M:Ti、Zr 和 Hf）蜂窝中量子反常霍尔效应的预测

背景

严谨的研究工作一直致力于探索新型二维材料，例如量子自旋霍尔 (QSH) 绝缘体。这些新型材料，也称为二维拓扑绝缘体 (2D TI)，表现出独特的特性，其中尽管体系统是绝缘体，但边缘仍具有自旋极化的无间隙状态 [1]。 QSH 绝缘体显示出无耗散的自旋/电荷传输，这在自旋电子器件应用中非常重要 [2]。最近，已经发现 QSH 绝缘体中时间反转对称性 (TRS) 的破坏会导致量子反常霍尔效应 (QAHE) 系统，其中螺旋边缘状态转换为手性边缘状态 [3]。无需外部磁场的无耗散电荷传输在低能耗自旋电子学中提供了有前景的应用 [4, 5]，并鼓励寻找更多的 QAHE 系统 [6, 7]。 Haldane 于 1988 年预测，QAHE 仅在 2013 年通过拓扑绝缘体的磁掺杂薄膜在实验上实现 [8]。理论研究表明，量子反常霍尔 (QAH) 相可以通过引入铁磁性并通过强自旋轨道耦合 (SOC) 效应诱导能带反转跃迁来打破 TI 的 TRS [9, 10]。因此，QSH 绝缘体是实现 QAHE 的良好起始材料。几项研究预测，IV 族 (Sn) [11-13] 和 V (Bi, Sb) [6, 14-17] 的薄膜支持 QSH 相，这也可以通过化学功能化实现 [17, 18]。除了 IV 族和 V 族元素外，还预测 [19-21] III-V 族蜂窝体在独立式和功能化情况下都支持 QSH 阶段。这些结果为寻找 QAHE 相铺平了道路。研究表明，QAHE 存在于官能化组 IV [22] 和 V [17, 18, 22] 薄膜中。此外，第一性原理计算表明 QAHE 在氟化 [23] 和化学功能化 [24] III-V 蜂窝中。此外，一些理论研究预测，蜂窝中的过渡金属掺杂可以诱导 QAH 相 [17, 25-27]。这已通过 Cr 和 V 掺杂实验实现 [8, 28, 29]。在 III-V 族蜂窝材料是 QSH 绝缘体的发现 [19] 和掺杂磁性材料可以诱导磁性的理论预测 [10] 的支持下，我们用过渡金属（M=Ti、Zr 和高频）。过渡金属碳化物 MC（M=Zr 和 Hf）[30] 和过渡金属卤化物 MX（M=Zr 和 Hf）[31] 也是预测作为 QSH 绝缘体存在的另一类材料。但是，尚未探索其支持 QAHE 的潜力。受这些发现的启发，我们预测了过渡金属 pnictides MPn（M=Ti、Zr 和 Hf；Pn=Sb 和 Bi）的电子特性，以表现出 QAH 相。在这项工作中，我们采用第一性原理计算来预测过渡金属（M =Ti、Zr 和 Hf）在 Bi/Sb 蜂窝上诱导内在磁性的能力。我们检查了屈曲和平面情况，并确定了由于应变引起的相变。通过计算Chern数和观测波段反演验证了QAH相位。

结果和讨论

类似于可以采用屈曲和平面结构的纯 Bi 蜂窝（晶胞中有两个原子），我们的材料是通过在晶胞中用过渡金属 [例如 Ti、Zr 和 Hf] 取代一半的 Bi 获得的. M-Bi/Sb 的顶视图与轮廓的 1 × 1 晶胞如图 1a 所示，而弯曲和平面 M-Bi/Sb 蜂窝的侧视图分别如图 1b、c 所示。图 1d 显示了相应的第一个布里渊区 (BZ)，标有高对称点。

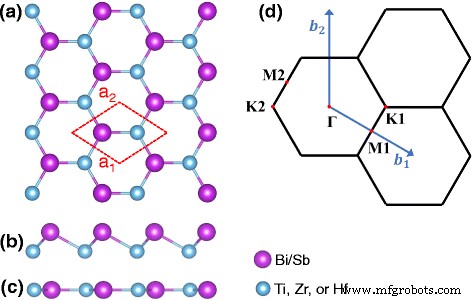
一 M-Sb/Bi蜂窝的晶体结构。 b , c 分别为弯曲结构和平面结构的侧视图。 d 具有高对称点的第一个布里渊带（BZ）

我们通过改变晶格常数并允许原子在屈曲和平面情况下松弛来研究蜂窝的稳定性和应变的影响。接下来，我们通过陈数计算确定了它们在不同应变下的拓扑相。结果通过图 2 所示的相图进行说明。TiBi、ZrBi 和 HfBi 的能量曲线分别显示在图 2a-c 中。我们发现 MBi 蜂窝具有低屈曲和平面相。通过这些数字，我们确定了用于进一步分析的平衡晶格常数。该图还表明，屈曲 MBi 是能量上最受青睐的结构。然而，当应变增加时观察到大部分 QAH 阶段，这将材料从弯曲的蜂窝状转变为平面蜂窝状。还应该注意的是，可以在屈曲 HfBi 中观察到 QAH 相，但只能在很小的晶格常数范围内观察到 [见图 2c]。

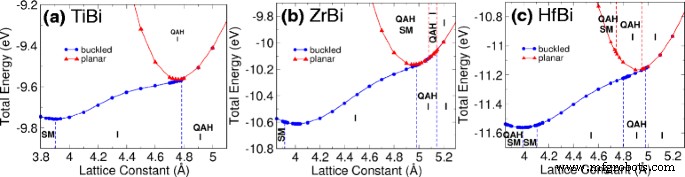
a的相图 TiBi，b ZrBi 和 c HfBi 显示了不同晶格常数下的总能量。该图分为标记为 QAH（量子异常霍尔相位）、I（绝缘体）和 SM（半金属）的各个区域。蓝色圆圈和红色三角形分别代表扣件和平面件

表 1 和 2 显示了 M-Bi 和 M-Sb 结构的平衡晶格常数。还指出了相关的带隙、磁矩、相位和材料分类。当计算出的陈数 C 为非零整数时，存在 QAHE。带隙计算为最低未占用带和最高占用带之间的差值。我们的计算表明，可以在平面 TiBi 和 HfBi 中发现 QAH 绝缘体相，带隙分别为 15 和 7 meV。此外，可以通过改变屈曲距离 [见图 3] 和通过在屈曲 HfBi 中引起应变 [图 3] 在 TiBi 中引起相变。 4]。在 TiBi 中，我们发现由于屈曲距离变化导致的带交叉出现在图 3d 所示的低对称点处；而在 HfBi 中，我们首先在 K2 (a =4.8 Å) 然后在 K1 (a =5.0 Å) 由于图 4c 中的应变，g。

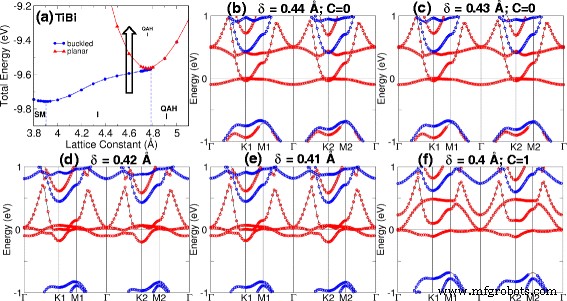
改变屈曲距离后的相变。 一 TiBi 在 a 处的相图 =4.6 埃。箭头显示了过渡的路径。 b –f 随着屈曲距离(δ ) 从 0.44 减少到 0.4 Å。转变发生在 δ =0.41 埃

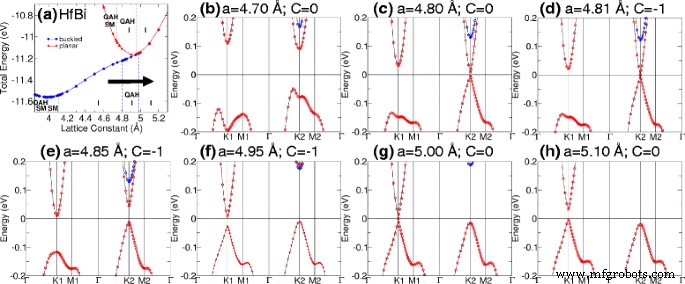
改变晶格常数后的相变。 一 屈曲 HfBi 的相图。箭头显示了过渡的路径。 b –h 随着晶格常数从4.7增加到5.1 Å，能带结构转变

图 5a、b 分别显示了 M-Bi 和 M-Sb 在平面和屈曲结构中在平衡晶格常数下的电子能带结构。红色和蓝色圆圈分别是向上旋转和向下旋转的贡献。 QAH 阶段（使用 C =1) 在平面 TiBi 中观察到的最大带隙为 15 meV。平面 HfBi 也是一种 QAH 绝缘体，具有 7 meV 的小带隙（具有 C =-1)。然而，在屈曲形式中，HfBi 是一种具有高 C 的半金属 =-3。另一方面，发现弯曲的 ZrBi、TiSb、ZrSb 和平面 ZrSb 是微不足道的绝缘体。

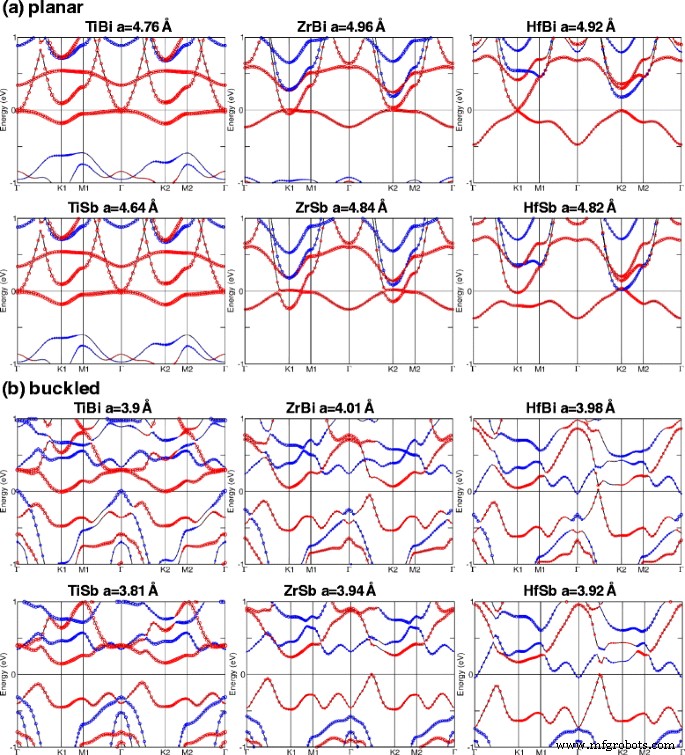
M-Pn（M=Ti、Zr 和 Hf；Pn=Sb 和 Bi）在 a 的平衡晶格常数下的电子能带结构 平面和b 扣箱。平衡晶格常数在能带结构上方给出。红色和蓝色圆圈表示 +s z 和 -s z 贡献，分别

通过检查 SOC 在非磁性和铁磁性计算中的影响，可以进一步了解 QAHE 的性质。为此，我们选择了平面 TiBi（带有 a =4.76 Å) 作为示例。在有和没有 SOC 的非磁性和铁磁性计算中获得的能带结构如图 6 所示。我们的计算表明这种结构的磁矩为 1.05 μ B 每个晶胞主要由 Ti 原子贡献。在非磁性计算中，我们发现该系统是金属的[图。 6a，c]。我们可以在图 6b 中观察到，由于受过渡金属 Ti 影响的铁磁有序，可以感应净磁矩。此外，该系统现在具有无间隙自旋向上状态（红线）和有间隙自旋向下状态，通过将 SOC 应用于铁磁计算，然后获得 15 meV 的间隙。这表明能带反转是由SOC引起的，并且QAHE中的间隙开放导致。

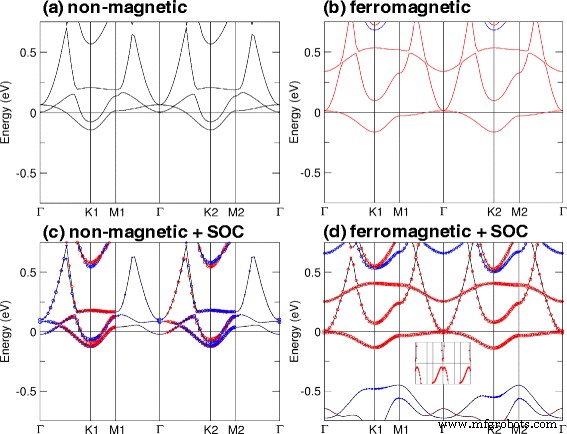
a处平面TiBi薄膜的电子能带结构 =4.76 Å 对于非磁性计算 (a ) 没有 SOC 和 (c ) 与 SOC 以及铁磁计算 (b ) 没有 SOC 和 (d ) 与 SOC。红色和蓝色圆圈表示 +s z 和 -s z 分别为 (c ) 非磁性 (d 铁磁）计算与 SOC

最后，我们使用通过万尼尔函数导出的紧束缚哈密顿量检查平面 HfBi 蜂窝的边缘带谱是否存在边缘状态。我们构建了具有锯齿形边缘和 127 Å 宽度的 HfBi 带，如图 7 所示。该图还证实了边缘状态的存在，这些边缘状态由分别代表左右边缘的红色和蓝色圆圈的大小表示并与其成正比.分离的边缘状态是由于左右锯齿形边缘的不对称性。我们还可以观察到奇数个边缘带穿过费米能级。我们发现这个数与陈数的绝对值相同，进一步证实了平面HfBi中的QAH相。

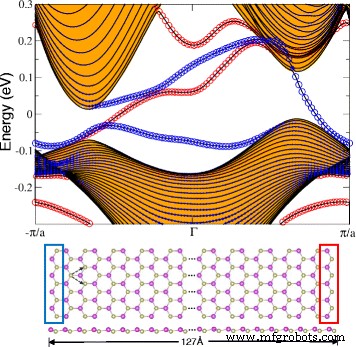
具有a的屈曲HfBi锯齿形纳米带边缘的能带结构 =4.9 Å，宽度为 127 Å。蓝色（红色）圆圈表示来自左（右）边缘的贡献。体带由橙色填充区域表示

我们进一步计算了每个系统的声子谱，并注意到这些系统具有负频率。因此，上述系统需要基板来稳定。我们还注意到，上述计算是使用一个一个的晶胞完成的，具有铁磁 (FM) 配置的材料是最稳定的状态。然而，对于更大的超级单元，我们发现FM在屈曲情况下仍然比反铁磁（AFM）配置具有更低的能量，而在平面情况下FM和AFM配置的能量均退化。

结论

总而言之，我们的第一性原理计算预测 Sb 或 Bi 蜂窝膜上的过渡金属（Ti、Zr 和 Hf）的替代可能会表现出 QAH 相。尽管这些材料在其屈曲形式下在能量上更稳定，但将其转化为平面形式会在相当合理的晶格常数范围内产生 QAH 相。这种相位也可以通过改变屈曲距离和应用我们计算出的相图中的应变来引起。我们发现平面 TiBi 和 HfBi 结构作为 QAH 绝缘体存在，带隙分别为 15 和 7 meV。这些发现提供了另一种在蜂窝材料中实现 QAH 相的方法，该材料可能在自旋电子应用中发挥作用。

方法/实验

密度泛函理论 (DFT) 框架内的第一性原理计算是使用在 Vienna Ab-Initio Simulation 中实施的广义梯度近似 (GGA) [32-36] 和投影仪增强波 (PAW) [37] 方法进行的包版本 5.3 (VASP) [38, 39]。将动能截止设置为 350 eV 并优化晶体结构，直到残余力不大于 5×10 ^-3 eV/Å。收敛的自洽标准设置为 10 ^-6 用于电子结构计算的 eV，有或没有自旋轨道耦合。我们通过沿 z 插入至少 20 Å 的真空层来模拟薄膜 24×24×1 Gamma 中心 Monkhorst-Pack 网格的采样二维布里渊区上的方向 [40]。我们使用 WANNIER90 包 [41] 计算了最大局部化的 Wannier 函数，然后将其用于计算边缘状态。拓扑相是通过使用 Z2Pack 包 [42, 43] 计算陈数来确定的，该包利用了一种跟踪混合万尼尔电荷中心的技术。