使用椭圆石墨烯-黑磷对的可调和各向异性双波段超材料吸收器

介绍

石墨烯是一种二维材料，碳原子排列成蜂窝状晶格[1, 2]。由于其超紧凑的尺寸和独特的光-石墨烯相互作用，近年来开发了各种基于石墨烯的光子器件 [3,4,5,6]。作为其最重要的应用之一，基于石墨烯的超材料吸收器由于其强大且可调谐的等离子体响应而引起了越来越多的兴趣 [7,8,9,10]。然而，由于石墨烯的带隙为零或接近零，一些需要高开关比的应用受到限制[11]。作为替代的二维材料，黑磷（BP）是一种单层磷原子，排列在六方晶格中，具有褶皱结构 [12]，最近也引起了研究兴趣的激增。它具有卓越的光学和电子特性，例如面内各向异性、厚度相关的可调带隙 [13] 以及高载流子密度和迁移率 [14]。在过去的几年中，在红外区域，研究人员已经研究了许多结构以增强基于 BP 的超材料中的光-BP 相互作用强度 [15,16,17]。然而，基于 BP 的吸收体的等离子体共振很难灵活有效地调整，并且它们通常具有相对较低的吸收率和中等掺杂水平。这是因为单层 BP 的共振强度相当弱，限制了其各向异性电位。因此，已经提出了基于石墨烯-BP 的等离子体吸收器，利用石墨烯和 BP 的杂交来实现强和各向异性的等离子体吸收 [18,19,20]。然而，之前报道的基于石墨烯-BP的吸收体通常需要相对复杂的制造技术或具有单一的吸收带，阻碍了它们在成像、生物传感和通信系统中的进一步应用。

在我们的工作中，使用周期性椭圆石墨烯-BP 对数值地提出了一种各向异性双波段红外吸收器，这很容易制造。证明了几何尺寸和掺杂水平对共振的独立可调性。绘制电场分布以揭示物理机制。还说明了入射角容差和偏振灵敏度。

方法

所提出的吸收体由沉积在 SiO2 层上的横向和纵向椭圆形石墨烯-BP 对组成，如图 1 所示。六方氮化硼 (hBN) 层插入单层石墨烯和 BP 之间作为绝缘间隔物以防止载流子传输它们之间并保证高载流子迁移率。 SiO2 和 hBN 的参数从参考文献中获得。 21 和参考。分别为 22。模拟由 COMSOL Multiphysics 执行，以研究双频带特性，该模拟基于频域中的有限元方法 (FEM)。我们应用 Floquet 周期性作为 x 的边界条件 - 和 y - 方向。计算域顶面设置红外波激发端口，底面设置完美电导体（PEC）边界条件。具有用户控制器网格密度的四面体网格应用于整个域。

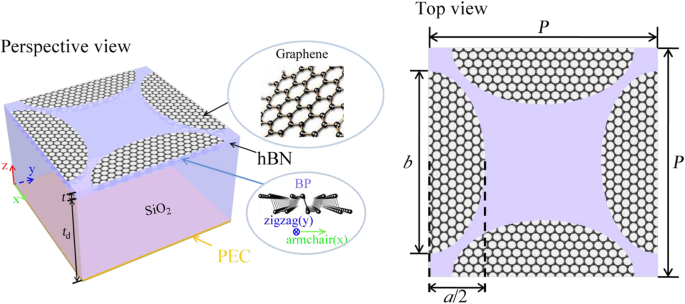
基于椭圆石墨烯-BP 对的拟议吸收体的晶胞。 t d 和 t 分别是介电层和绝缘体层的厚度。 一 和 b 是椭圆的短轴和长轴。 P 是方形晶胞的周期边长

在模拟中，石墨烯和 BP 都被视为具有表面电导率的二维表面，而不是具有介电常数张量的大块材料。该假设解决了超薄材料厚度定义和计算效率低的问题[23]。

描述石墨烯的表面电导率σ (ω )，我们使用如下著名的 Kubo 公式[24]：

根据方程。 1、σ (ω ) 由带内和带间对应物组成，即 σ 内部和σ 间。 ω 是弧度频率，μc 是化学势，Г 是散射率，T 是开尔文温度。 ㄧ , e , ξ , 和 k B 分别为约化普朗克常数、电子电荷、电子能量和玻尔兹曼常数。

在红外区域，由于入射光子几乎不能激发带间跃迁，光-石墨烯相互作用以带内跃迁为主。特别是当 μc ≫ k BT ，久保公式可以进一步简化为方程。 5：

因此，石墨烯的表面电导率取决于ω的值 , Г , 和 μ c .在这里，Г 假定为 0.3 meV 和 μ 根据之前的工作[25, 26]，假设c为0.7 eV。

另一方面，我们计算表面电导率σ j的BP与简单的半经典德鲁德模型[27]：

其中 n s 是与掺杂水平相关的载流子密度。我们选择n s =1.9 × 10 ¹³ cm ⁻² 和 Г BP = 10 meV 根据之前的参考文献 [16]。 j 是关注的方向，所以 σ x 和 σ 是 由沿 x 的电子质量决定 - 和 y - 方向，分别。 米 x 和 m y 可以通过以下方式进一步计算：

其中 m 0 是标准电子质量，Δ 和 a 分别是 BP 单层的带隙和尺度长度。通过替换方程。 10-12 进入方程。 8 和方程。 9、可以得到沿着扶手椅的电子质量 (x -) 和锯齿形 (y -） 方向。它们之间的差异导致了BP的各向异性表面电导率。

结果与讨论

为了说明所提出的吸收体的各向异性吸收特性，我们首先模拟和比较单个石墨烯层、单个 BP 层和石墨烯-BP 对的吸收光谱。从图 2a 中可以看出，石墨烯的等离子体响应是各向同性的，在 9.9 μm 和 15.4 μm 处有两个明显的吸收峰，与极化无关。另一方面，尽管 BP 的等离子体共振是各向异性的，但其强度对于 TE (<12.7%) 或 TM (<0.7%) 入射都很弱。通过结合石墨烯和 BP 的优点，石墨烯-BP 对表现出强烈的和各向异性的等离子体响应。对于TE入射，两个吸收峰位于8.8 μm和14.1 μm，吸收率大于90%。对于 TM 入射，最大吸收波长分别移动到 9.5 μm 和 15.4 μm。偏振消光比可以定义为 PER =10 × log(R 1/R 0)，其中 R 1 和 R 0 表示反射率 (R =1-A , A 表示同一波长下不同极化的吸光度），则每个共振的最大PER值在λ处可达23 dB和25 dB =9.5 μm 和 λ =14.1 μm，分别。因此，所提出的吸收器可以用作高性能的双波段反射偏振器。

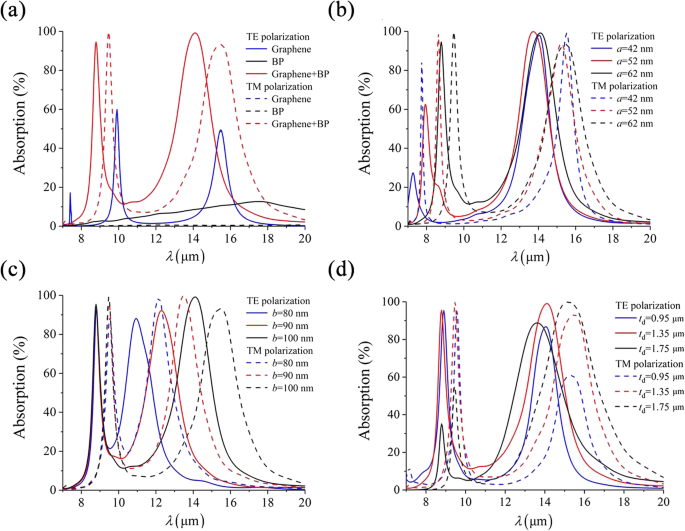
一 单层石墨烯（蓝色实线和蓝色虚线重叠）、单层BP和石墨烯-BP对之间等离子体响应的比较，以及不同a的吸收光谱 (b ), b (c ) 和 t d (d ）。默认参数为 a =62 nm, b =100 nm, t d =1.35 μm, t =5 nm，并且 P =250 nm，正常入射下

我们接下来分析具有不同几何配置的吸收光谱，以证明图 2b-d 中的可调双波段吸收特性。在图 2b 中，第一个吸收峰的红移为 a 对于两种极化，从 42 到 52 nm 增加，而第二谐振频率几乎没有变化。另一方面，如图2c所示，通过增加长轴长度b ，第二个共振也发生红移，而第一个吸收峰对于 TE 和 TM 极化保持不变。因此，可以通过改变椭圆形石墨烯-BP 对中相应的轴长度来独立调整双吸收峰。此外，介电层的厚度对所提出的器件的性能也起着关键作用，该器件充当由石墨烯-BP 超表面和 PEC 衬底形成的法布里-珀罗谐振器。因此，不同t的吸收光谱 d 绘制在图 2d 中。作为 t d从0.95增加到1.75 μm，TE和TM极化的第一个吸收峰急剧下降，而第二个峰先增加后急剧下降。因此，存在最佳厚度 t d 使所提出的吸收体的双吸收峰最大化。

为了阐明物理洞察力，我们进一步揭示了图 3 中不同波长处的电场强度分布。对于 TE 入射，电场位于扶手椅 (x -） 方向。在第一个峰值 (λ =8.8 μm)，入射的红外光可以激发石墨烯和BP中的电子横向振荡，导致电场在纵向椭圆的短轴端集中，如图3a所示。在 λ =14.1 μm，横向椭圆长轴端的局域电场增强。另一方面，在锯齿形 (y -)方向可以激发电子在9.5 μm的吸收峰沿纵向振动，导致横向椭圆短轴端的场分布集中。此外，在 λ =15.4 μm，电场增强集中在纵向椭圆的长轴端。因此，共振波长与横向和纵向椭圆形石墨烯和BP对中感应偶极子的有限振荡长度直接相关。

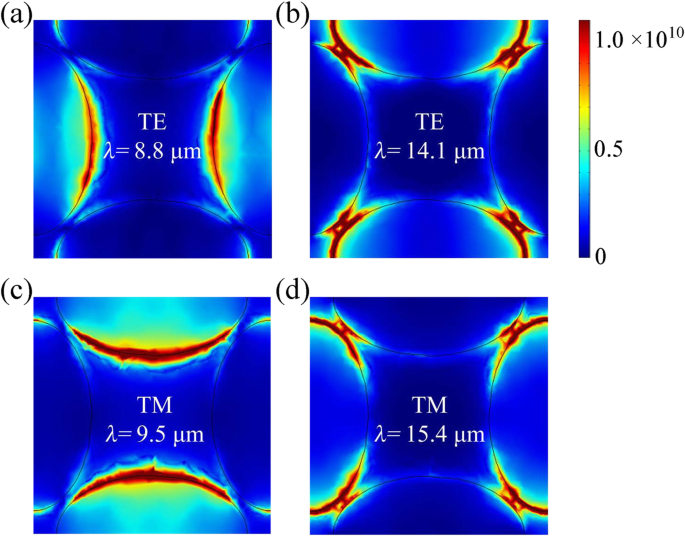
a在不同波长下的电场强度分布 , b TE 和 c , d TM极化，其中a =62 nm, b =100 nm, t d =1.35 μm, t =5 nm, P =250 nm，正常入射下

可以通过改变几何尺寸来有效地调整各向异性双波段吸收性能，如图 2b-d 所示。同时，石墨烯和BP的表面电导率也可以通过改变μc和n来控制 s 根据上述石墨烯和 BP 模型公式。 μ c 和 n s 代表在几何制造后可以改变的石墨烯和 BP 的掺杂水平。因此，具有不同 μ 的拟议吸收器的性能 c 和 n s如图4所示。考虑到实际情况，μ c 是在 0.4 和 0.8 eV 之间选择的，从之前的工作中得到了实验验证 [28]。在之前报道的工作 [29] 中，n 的最大理论值 BP 的 s 被证明是 2.6 × 10 ¹⁴ cm ⁻² , 所以适度的 n s 在 10 ¹³ 之间选择 cm ⁻² 和 10 ¹⁴ cm ⁻² 在模拟中。在图 4a 中，当 μ c =0.4 eV，第一个吸收峰位于10.9 μm，第二个吸收峰位于17.1 μm。作为 μ c 增加到 0.8 eV，两个谐振波长蓝移到 8.4 μm 和 13.4 μm。与 TM 极化类似，双吸收峰分别从 12.4 和 19.8 μm 蓝移到 8.9 和 14.4 μm，μ c 从 0.4 增加到 0.8 eV，如图 4b 所示。对于单个图案化 BP，共振波长 λ p 可以计算为 \( {\lambda}_p\propto \sqrt{L/{n}_s} \)，其中 L 是有效振荡长度 [27]。因此，如果 L 固定，吸收光谱表现出明显的蓝移 n 如图 4c 所示，TE 极化的 s 增加。对于 TM 偏振，吸收峰也略微蓝移为 n s 从 10 ¹³ 增加 cm ⁻² 到 10 ¹⁴ cm ⁻² 如图 4d 所示。

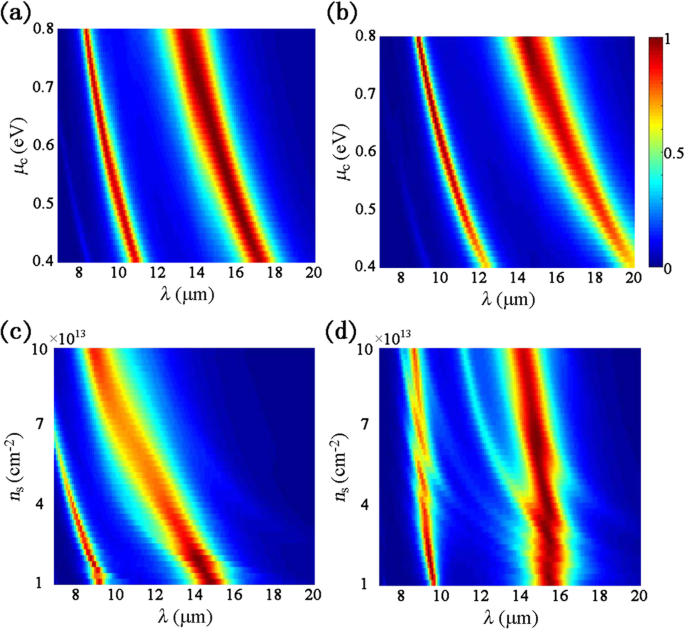
吸收光谱与法向入射下不同掺杂水平的关系：a 和 b 对于石墨烯的不同化学势，c 和 d 对于不同载流子密度的 BP，a 和 c 对于 TE 极化，和 b 和 d 对于 TM 极化，其中 a =62 nm, b =100 nm, t d =1.35 μm, t =5 nm，并且 P =250 nm

在实际应用中，红外吸收剂优选具有宽入射角的容差。因此，详细阐述了斜入射下的吸收光谱。在图 5a 中，观察到对于 TE 极化，当 θ 时，第一个吸收峰保持大于 80% 增加到 52°，而第二个吸收峰即使 θ 也保持在 80% 以上 增加到 80°。当 θ> 46°，第二谐振波长随着θ逐渐红移 变得更大。对于 TM 入射，当 θ 小于62°，第一个峰的吸收率保持大于90%，而谐振波长保持恒定在λ =9.5 μm，如图5b所示。此外，对于第二次共振，θ 的峰值吸收保持大于 80% 到 60°，然后随着 θ 的增加略有下降 .优异的角稳定性源于法布里-珀罗谐振器的共同特征，它们对斜入射角具有鲁棒性[30]。

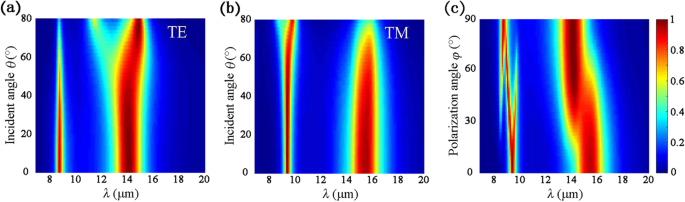
a在不同入射角下的吸收光谱 TE 和 b TM极化和c 法向入射下的各种偏振角。几何参数同图4

不同偏振角垂直入射下的吸收光谱φ 在图 5c 中呈现，以研究所提出的吸收器的偏振依赖性。我们假设 TE 极化的极化角为 0°。从图 5c 中可以看出，当 φ 从 0°增加到 90°，吸收光谱与图 2a 中的 TM 偏振相同。当 0° <φ <90°，入射将激发 BP 中的电子在扶手椅和锯齿形方向上振荡，因为它的 x - 和 y - 入射电场的分量。因此，可以同时在BP的扶手椅和Z字形方向上诱导表面等离子体共振。

结论

总之，我们提出了一种由周期性横向和纵向石墨烯-BP 椭圆组成的各向异性双波段红外吸收器。每个谐振的最大 PER 可以达到 23 dB 和 25 dB。双各向异性共振归因于位于短轴和长轴末端的感应电偶极子。通过调整短轴和长轴的长度，可以分别独立调谐第一和第二吸收峰。此外，还可以通过改变石墨烯和 BP 的相应掺杂水平来调整共振吸收带。此外，在任何偏振的斜入射下都可以实现两个峰的高吸收率。所提出的吸收体可用作可调反射偏振器和新型红外传感器。

数据和材料的可用性

所有数据完全可用，不受限制。

缩写

BP：

黑磷

有限元：

有限元法

hBN：

六方氮化硼

PEC：

完美的电导体

TE：

横向电动

TM：

横磁