使用分子动力学研究石墨烯在金基材上的纳米级摩擦行为

背景

石墨烯是一种有前景的新材料，可用于纳米级电子产品，具有广泛的潜在应用 [1,2,3,4,5]。在实际的基于石墨烯的电子设备中，金通常用于电触点 [6]。因此，石墨烯-金体系的摩擦在此类石墨烯器件的高效制造和可靠运行中起着重要作用。尽管石墨烯因其优异的机械性能引起了纳米摩擦学领域研究人员的极大兴趣 [3, 7]，但石墨烯在金表面滑动的摩擦性能却知之甚少。到目前为止，石墨烯的许多摩擦学研究都集中在石墨烯和扫描探针尖端之间的摩擦力上 [8,9,10,11,12,13,14]。例如，化学改性石墨摩擦的原子力显微镜 (AFM) 实验显示负摩擦系数 [9]。少层石墨烯的摩擦力显微镜 (FFM) 实验发现，随着石墨烯层数的减少，摩擦力增加 [10, 11]。这些现象可以通过石墨烯的起皱效应来解释 [9,10,11]。据推测，石墨烯薄片和石墨之间的摩擦是在在石墨上滑动过程中尖端拖动薄片时测量的 [8, 14]。研究发现，由于薄片重新定向成相称的结构，旋转运动与薄片横向运动相结合，导致摩擦增加 [15]。同时，一些学者也致力于使用其他技术研究石墨烯和/或金的摩擦。采用石英晶体微量天平 (QCM) 技术研究金在石墨烯上的润滑性 [16] 和石墨烯/Ni(111) 基板上固体氙膜的滑动摩擦 [17]。 QCM 实验和分子动力学 (MD) 模拟都表明，非公度 Kr 单层在 Au 上的摩擦遵循粘性摩擦定律 [18, 19]。进行 MD 模拟以探索石墨基板上二维金岛和三维金簇的静摩擦 [20]。发现由于厚簇具有更高的有效刚度，滑块厚度可以促进润滑性。通过对石墨烯和金衬底上氙原子的 MD 模拟 [21] 也揭示了尺寸相关的界面可公度性，这与 Cu 衬底上氪和硅团簇的模拟一致 [22]，这可以解释静摩擦的尺寸依赖性。最近，在低温下观察到了 Au(111) 衬底上石墨烯纳米带的超润滑性 [23]。基特等人。直接测量了石墨烯在 SiO2 基板上滑动的摩擦，发现单层和双层石墨烯的摩擦行为违反了阿蒙顿定律 [24]。总体而言，作为一种纯二维材料，预计石墨烯对石墨烯-基板系统表现出非典型的摩擦行为是合理的。遗憾的是，尽管已经系统地探索了石墨烯和金属之间的界面性质，但仍然缺乏对石墨烯在金衬底上滑动摩擦的详细研究[25,26,27,28]。

为了填补这一空白，在本文中，使用分子动力学 (MD) 模拟彻底研究了移动石墨烯薄片在单晶金基板上的滑动摩擦行为。我们研究了薄片尺寸、薄片形状、薄片与衬底之间的相对旋转角以及衬底晶体取向的影响，以阐明摩擦性能。

方法

模拟方法

为了模拟通过弹簧连接到尖端的石墨烯薄片在金基板上滑动的 AFM 实验 [29]，我们建立了由 N 制成的石墨烯薄片组成的 MD 模型 原子和单晶金基板，见图1。基板底部的三层原子在空间中保持固定，作为边界原子。为了控制系统的温度，选择与衬底中边界原子相邻的四层原子作为恒温原子。恒温器原子通过速度缩放方法保持在 300 K 的恒定温度 [30]。在本文中，首先，我们不考虑滑动过程中石墨烯的旋转；石墨烯中的原子只允许在 x 中移动 和 z 方向，但被限制在 y 方向，这简化了模拟。这是本文的主要关注点。然后，我们进一步进行了一些 MD 模拟，而没有石墨烯在 y 中的运动约束 方向以更好地匹配真实的实验条件。片状原子被一个虚拟原子以恒定速度通过谐波弹簧拖动。平行于基板表面的弹簧具有 10 N/m 的横向刚度，用于表示 AFM 系统的悬臂梁和尖端的变形 [31]。在模拟 [29, 31] 中，恒定的法向载荷直接施加到片状原子上。石墨烯薄片被虚拟原子以 10 米/秒的恒定速度横向拉动。运动方程与速度-Verlet 算法相结合。时间步长为 1 fs。边界在 x 中是周期性的 和 y 方向，在 z 自由 方向。

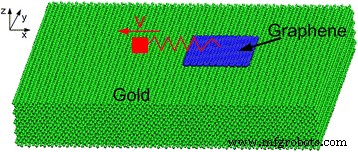
摩擦过程仿真模型

为了研究衬底晶体取向的影响，我们分别在 Au(111)、(001) 和 (110) 平面的三个不同表面上进行滑动摩擦的 MD 模拟。对于Au(111)面，坐标系取为\( x-\left[11\overline{2}\right] \), \( y-\left[1\overline{1}0\right] \) ) 和 z -[111] 大小为 19.98 × 15.0 × 3.06 nm ³ .对于Au(001)面，坐标系为x -[100], y -[010] 和 z- [001] 基板尺寸为19.99 × 15.1 × 3.06nm ³ .对于Au(110)面，坐标系为x -[001]、\( y-\left[1\overline{1}0\right] \) 和 z -[110] 大小为 19.99 × 15.0 × 3.03 nm ³ . Au(111)、Au(110) 和 Au(001) 表面沿滑动方向的晶格间距分别为 9.99 Å、4.08 Å 和 4.08 Å。如果没有注明，则采用 Au(111) 作为基材。在模拟中，模拟了几种不同的薄片尺寸和形状。默认薄片形状是大小为 5.8 纳米的正方形（原子数 N =1344）。 x -axis 沿着石墨烯的扶手椅方向和 y -axis 沿锯齿形方向，z - 垂直于石墨烯的轴。

Au 内的原子间力源自嵌入原子法 (EAM) 势 [32]。 EAM 势在模拟各种金属的弹性特性、缺陷形成能和断裂机制方面非常成功 [32, 33]。它也已成功应用于描述金属的表面特性，例如表面能和表面重建 [32,33,34]。广泛使用的 AIREBO 势用于描述石墨烯内原子的相互作用 [35]。石墨烯和 Au 基板之间的相互作用由标准 Lennard-Jones (LJ) 电位建模，该电位已被用于研究许多非平衡现象，例如石墨上金簇的摩擦和扩散 [36, 37]。 LJ 参数 [28, 29] 为：ε =22.0 meV 和 σ =2.74 Å。 MD 模拟是使用大规模原子/分子大规模并行模拟器 (LAMMPS) [38] 进行的。在模拟中，石墨烯薄片最初位于 Au 基板表面上方。摩擦系统完全松弛后，虚拟原子开始沿负x滑动 方向匀速。

结果和讨论

图 2 显示了摩擦力在各种法向载荷下作为滑动距离的函数。在本文中，滑动距离是虚拟原子的滑动距离。在 AFM 实验中，通过弹簧的变形来测量摩擦力。石墨烯薄片呈方形，大小为 5.8 nm，由 1344 个原子组成。很明显，摩擦力持续增加，然后急剧下降，这是典型的粘滑运动。摩擦力的突然下降导致能量耗散，并意味着在具有局部势能最小值的多个亚稳态之间发生转变 [39]。摩擦力随着负载 L 的增加而增加是合理的。为了探索尺寸效应，另外两个尺寸为 2.0 nm (N =160 个原子）和 10.0 nm (N =3936 个原子）。滑动过程中不同薄片尺寸的摩擦力和平均摩擦力的变化如图3所示。对于5.8-nm的薄片，2.0-和10-也可以观察到明显的粘滑摩擦纳米薄片。此外，每个原子的平均摩擦力明显存在尺寸效应F fric/N，见图 3c。相同载荷下，每个原子的平均摩擦力F 对于较小的薄片，fric/N 较大。这种尺寸效应是由于随着薄片尺寸的增加，边缘在摩擦中的作用逐渐降低 [40, 41]。应该注意的是，QCM 实验和 MD 模拟都发现吸附簇的摩擦随着其尺寸的增加而降低 [18,19,20,21,22]，与我们的模拟一致。然而，QCM 实验和 MD 模拟中摩擦的尺寸依赖性可以通过尺寸相关的界面公度来解释 [18,19,20,21,22]。

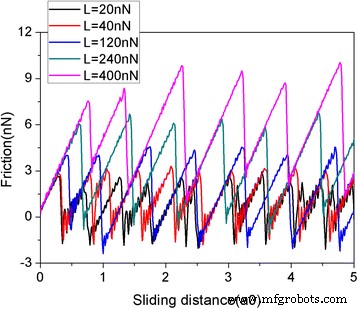
在各种法向载荷 (L) 下，摩擦力作为滑动距离的函数。薄片呈方形，大小为 5.8 纳米。其中，a0 (=9.99 Å) 是 Au(111) 沿滑动方向的晶格间距

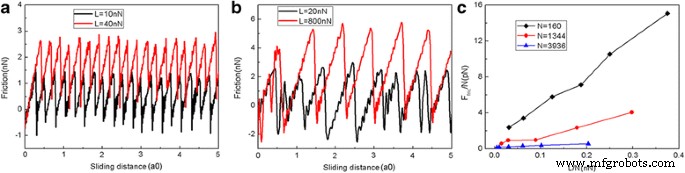
不同薄片尺寸的摩擦力和平均摩擦力的变化。作为滑动距离函数的典型摩擦力为 2.0 nm (N =160 个原子) 片状 (a ) 和 10 纳米 (N =3936 个原子）片状 (b ）。 c 每个原子的平均摩擦力 (F fric/N) 作为每原子载荷 (L/N) 的函数。其中，a0 (=9.99 Å) 是 Au(111) 沿滑动方向的晶格间距

由于滑块形状在确定摩擦方面起着重要作用 [42, 43]，为了进一步探索薄片形状对摩擦过程的影响，我们还使用圆形石墨烯薄片 (N =1080 个原子）和三角形石墨烯薄片 (N =654 个原子）。图 4 显示了滑动过程中不同薄片形状的典型摩擦力和平均摩擦力的变化。如图 4a、b 所示，在小负载 (L =20 nN 圆形薄片和 L =10 nN（三角形薄片），摩擦力在零附近连续波动，可以观察到超低摩擦（超润滑性）。然而，在大的正常负载 (L =400 nN 圆形薄片和 L =200 nN（三角形薄片），薄片表现出明显的粘滑运动和大摩擦力 [39]。相同载荷下，每个原子的平均摩擦力F fric/N 方片最大，三角形片最小，而 F 圆形薄片的 fric/N 介于两者之间。此外，每个原子的平均摩擦力的差异F 圆形和三角形薄片之间的 fric/N 相当小。但是F 方形薄片的 fric/N 大得多。因此，很明显薄片形状在滑动过程中起着至关重要的作用。

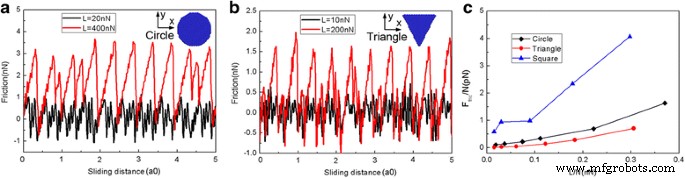
不同薄片形状的摩擦力和平均摩擦力的变化。作为圆形滑动距离函数的典型摩擦力 (N =1080 个原子）片状 (a ) 和三角形 (N =654 个原子) 片状 (b ）。 c 每个原子的平均摩擦力 (F fric/N) 作为每原子载荷 (L/N) 的函数。其中，a0 (=9.99 Å) 是 Au(111) 沿滑动方向的晶格间距

众所周知，薄片相对于基材的取向对于确定摩擦也很关键[42]。为了探索取向对摩擦的影响，石墨烯薄片围绕 z 逆时针旋转不同的角度 - 轴垂直于接触。旋转角度0°（不旋转）对应x -axis 沿着石墨烯的扶手椅方向，而旋转角 90° 对应于 x 的情况 -axis 沿之字形方向。在 L 处具有不同旋转角度的 5.8 nm 方形薄片的摩擦力随滑动距离的变化 =240 nN 如图 5. 对应的平均摩擦力 F 不同法向载荷下不同旋转角度下的摩擦系数计算如图6所示。很明显，对于θ =15°和θ =45°的薄片，摩擦力在零附近连续波动，可以观察到超润滑性，见图. 5b，d。此外，可以观察到 θ =15° 和 θ =45° 的薄片的平均摩擦力差异很小，见图 6。然而，对于 θ =30°、60° 和 θ =90° 的薄片，薄片表现出明显的粘滑运动和较大的摩擦力。此外，对于θ =30°、60°和θ =90°的薄片，旋转角度越大，平均摩擦力越大。有旋转的薄片的摩擦力都比不旋转的薄片的摩擦力小很多（θ =0°）。

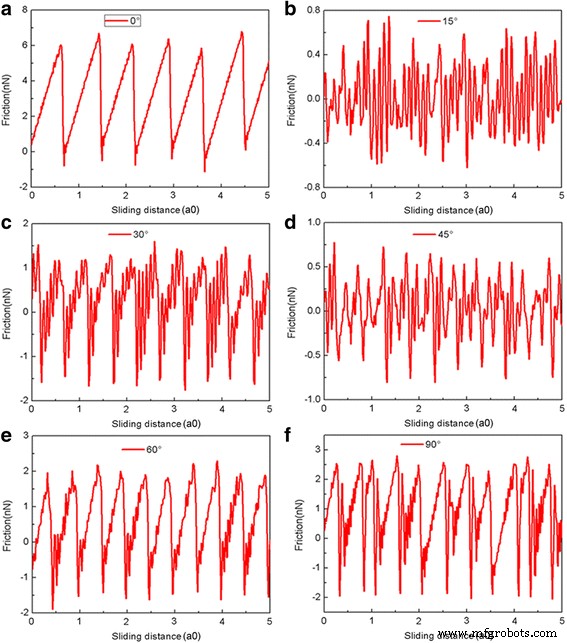
L 处 5.8 nm 方形薄片的摩擦力与滑动距离的关系 =240 nN 用于不同的旋转角度（θ =0°、15°、30°、45°、60°、90°）。 一 –f 分别对应旋转角度0°~90°。其中，a0 (=9.99 Å) 是 Au(111) 沿滑动方向的晶格间距

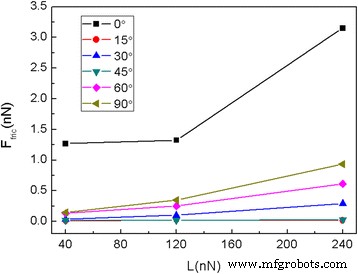
5.8nm方形薄片在不同法向载荷下不同旋转角度的平均摩擦力Ffric

单晶金表现出显着的各向异性效应的事实鼓励我们进一步研究基板的晶体取向对摩擦过程的影响。我们对晶体取向和滑动方向的另外两种组合进行了 MD 模拟，即 (001) [100] 和 (110) [001]。摩擦力和平均摩擦力F 在具有不同晶体取向的 Au 衬底上滑动的 5.8 nm 方形薄片的 fric 显示在图 1 和图 2 中。分别为 7 和 8。正如预期的那样，摩擦力随着法向载荷的增加而增加。可以看出，在相同载荷下，Au(001)和Au(110)面的摩擦力大于Au(111)面的摩擦力，Au(110)面的摩擦力为最大的。

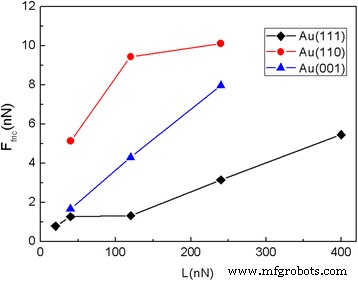
5.8 nm 方形薄片在 (a ) Au(001) 和 (b ) Au(110) 表面作为不同法向载荷下滑动距离的函数。这里，a1 (=4.08 Å) 是 Au(001) 沿滑动方向的晶格间距，a2 (=4.08 Å) 是 Au(110) 沿滑动方向的晶格间距

平均摩擦力F 不同法向载荷下5.8nm方形薄片在不同晶向的Au衬底上滑动的摩擦系数

根据著名的 Prandtl-Tomlinson 模型 [44]，摩擦力与界面能波纹密切相关 [45,46,47]。为了探索摩擦的显着各向异性效应背后的潜在机制，我们计算了随着我们改变薄片位置而在薄片和 Au 基板之间的相互作用势能 [46]。势能是针对固定高度的刚性薄片计算的，该高度对应于给定负载的平均高度 [29]。三个典型的等高线图表示 L 处 Au(111)、Au(110) 和 Au(001) 表面势能的空间变化 =120 nN 分别显示在图 9a-c 中。为了获得图 9 中的势能面 (PES) 图，我们沿 x 使用了 21 个网格点 和 y 方向。在图 9 中，为 Au(111)、Au(110) 和 Au(001) 计算的能量波纹分别为 3.5 eV、66.6 eV 和 29.1 eV。在图 9a-c 中，黑色实线 (y =0) 在 PES 地图上用于显示薄片的滑动路径。图 9d-f 中还分别绘制了沿 Au(111)、Au(110) 和 Au(001) 滑动路径的石墨烯-金相互作用势能。图 9 中 Au(111)、Au(110) 和 Au(001) 沿滑动路径的能量波纹分别为 3.5 eV、59.7 eV 和 29.1 eV。可以清楚地看出，能量波纹的幅度表现出与摩擦相同的各向异性效应。 Au(001)和Au(110)面的能量波纹大于Au(111)面的能量波纹，Au(110)面的能量波纹最大。因此，这清楚地解释了滑动过程中摩擦的显着各向异性效应 [45,46,47]。摩擦力随着石墨烯-衬底相互作用强度（能量波纹）的降低而降低的发现与MD模拟[16]和QCM实验[17]一致。

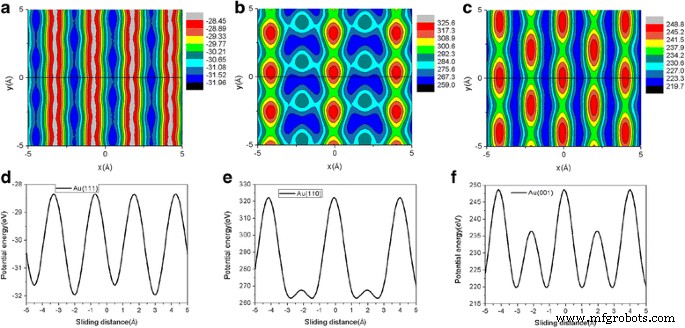
L 处 Au(111)、Au(110) 和 Au(001) 表面势能的等值线图 =120 nN 显示在 a 中 –c ， 分别。采用 5.8 nm 方形石墨烯薄片。在 a –c , 黑色实线 (y =0) 在地图上用于显示薄片的滑动路径。沿着Au(111)、Au(110)和Au(001)表面滑动路径的石墨烯-金相互作用势能也绘制在d中 –f ， 分别。势能的单位是eV。 L处的薄片平均高度 =120 nN 对于 Au(111)、Au(110) 和 Au(001) 表面分别为 2.36 Å、2.1 Å 和 2.17 Å

为了更好地匹配真实的实验条件，我们进一步进行了滑动摩擦的MD模拟，没有石墨烯在y中的运动约束 方向，在这种情况下，薄片可以在 y 中旋转和移动 方向。图 10 显示了在各种法向载荷下摩擦力与滑动距离的函数关系，该石墨烯薄片由 1344 个原子组成，具有方形和 5.8 nm 的尺寸。虽然摩擦力的值发生了变化，但可以看出摩擦力不断增加，然后突然下降，这是一种类似于图 2 的明显粘滑运动。摩擦力如预期的那样随着负载的增加而增加。我们还研究了另外两个尺寸为 2.0 nm (N =160 个原子）和 10.0 nm (N =3936 个原子）没有石墨烯在 y 中的运动约束 方向。滑动过程中不同薄片尺寸的摩擦力和平均摩擦力的变化如图 11 所示。与图 3 类似，我们还观察到 2.0 和 10 纳米薄片的明显粘滑摩擦。此外，每个原子的平均摩擦力存在尺寸效应F fric /N，见图 11c。在相同载荷下，每个原子的平均摩擦力F 对于较小的薄片，fric/N 较大，这是摩擦的典型尺寸效应。总的来说，我们发现 y 摩擦过程的 MD 模拟的主要发现 -放宽石墨烯薄片在y中的运动约束后，薄片的方向运动仍然成立 滑动时的方向。

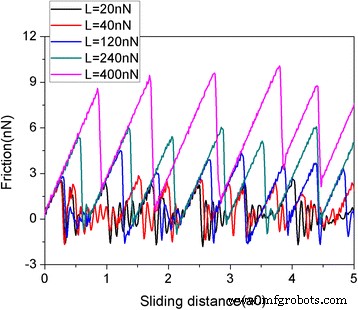
在各种法向载荷 (L ) 对于没有石墨烯在 y 运动约束的摩擦过程 方向。薄片呈方形，大小为 5.8 纳米。其中，a0 (=9.99 Å) 是 Au(111) 沿滑动方向的晶格间距

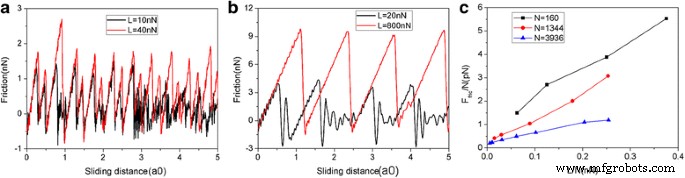
y中没有石墨烯运动约束的摩擦过程中不同薄片尺寸的摩擦力和平均摩擦力的变化 方向。作为滑动距离函数的典型摩擦力为 2.0 nm (N =160 个原子) 片状 (a ) 和 10 纳米 (N =3936 个原子）片状 (b ）。 c 每个原子的平均摩擦力 (F fric/N) 作为每原子载荷 (L/N) 的函数。其中，a0 (=9.99 Å) 是 Au(111) 沿滑动方向的晶格间距

结论

在这项工作中，分子动力学模拟被用来研究移动石墨烯薄片在单晶金基板上的滑动摩擦行为。深入研究了薄片尺寸、薄片形状、相对旋转角和衬底晶体取向的影响。发现摩擦行为存在尺寸效应。相同载荷下，每个原子的平均摩擦力F 对于较小的石墨烯薄片，fric/N 较大。还发现薄片形状在摩擦过程中起重要作用。每个原子的平均摩擦力 F 方形薄片的 fric/N 比三角形和圆形薄片的 fric/N 大得多。此外，每个原子的平均摩擦力 F 三角形薄片的 fric/N 最小。我们还发现石墨烯薄片相对于 Au 基板的取向影响对于确定摩擦至关重要。石墨烯薄片沿扶手椅方向滑动的摩擦力远大于旋转的薄片的摩擦力。对于 θ =15° 和 θ =45° 的薄片，可以观察到超低摩擦力。此外，对于θ =30°、60°和θ =90°的薄片，旋转角度越大，摩擦力越大。此外，发现摩擦表现出显着的各向异性效应。 Au(001)和Au(110)面的摩擦力大于Au(111)面的摩擦力，Au(110)面的摩擦力最大。这种摩擦的各向异性效应归因于势能波纹的各向异性效应。这些结果不仅提供了对石墨烯薄片在金衬底上滑动的潜在机制的见解，而且可以指导纳米级石墨烯基器件的设计和制造。