从反铁磁 MnBr2 到具有大 MAE 的铁磁 Mn3Br8 单层的对话

介绍

自旋电子学利用电子自旋和相关的磁矩，在过去的几十年里引起了广泛的关注 [1]，因为它比基于电荷的设备具有独特的优势。最近在有限温度下实现具有长程磁性排序的二维 (2D) 铁磁体 [2, 3] 对纳米级自旋电子学和相关应用具有重要意义，并激发了研究和制造二维铁磁体的巨大努力 [4,5 ,6,7,8,9]。

2017 年实现了前两种具有原子厚度的二维铁磁体，即单层 CrI3 [2] 和双层 Cr2Ge2Te6 [3]。不幸的是，它们的居里温度都低于液氮温度 (77 K)，这限制了它们的实际应用。除了居里温度外，实际应用中还需要相当大的磁各向异性和磁矩。大的磁各向异性能 (MAE) 意味着磁序有利于对抗热波动，并有可能降低每比特信息的粒度；小的 MAE 可能导致超顺磁性而不是铁磁性。大磁矩为自旋电子学提供了更高的灵敏度、更高的效率和更高的密度。重元素由于其强大的自旋轨道耦合 (SOC) 效应，更有可能带来大的 MAE [10]。一系列由重元素组成的 2D FM 材料已被预测具有大 MAE，例如 CrI3 [11]、CrAs [12]、CrSeI [13]、CrSiTe3 [14]、CrWI6 [15]、FeBr2 和 FeI2 单层 [16] ]。此外，MXenes Mn2NF2 和 Mn2N(OH)2 Mn 原子上的局部磁矩为每个 Mn 原子 4.5μB [17]，是已报道的 FM 2D 材料中最大的。

由于成功合成了 CrI3 单层，过渡金属卤化物备受关注 [18,19,20,21,22,23,24,25,26,27]。在双层 MnF2 中观察到自旋回波效应 [20]；磁性隧道结 (MTJ) [21] 中已经实施了几层 CrI3； NiCl3 单层已被预测为一种新型的狄拉克自旋无隙半导体 (SGS) [22]。特别是，基于第一性原理计算，MnBr2 单层具有 0.25 meV MAE 沿垂直于平面的反铁磁性[16]；锰 ²⁺ 离子在 d ⁵ 具有 5μB 磁矩的高自旋状态 [16, 26]。这些结果暗示了 MnBr2 作为具有大磁矩的单层铁磁体的潜力。关键问题是如何将Mn离子之间的AFM耦合转化为FM耦合。

通过实验在 LaMnO3 薄膜中观察到显着的 Mn 空位密度 [28]，并且可以通过高能粒子辐照或化学蚀刻有意调节合成过程来控制缺陷浓度 [29]。在这种情况下，我们通过将单个 Mn 空位引入 MnBr2 单层来设计 Mn3Br8 单层。空位改变了Mn原子的配位结构，破坏了d ⁵ 构型，这可能会将反铁磁耦合转化为铁磁耦合，并由于重 Br 原子而带来大的 MAE。正如我们所期望的，Mn3Br8 单层是 FM 并且每个分子式单元具有 - 2.33 meV 的大 MAE，每个 Mn 原子的磁矩为 13/3μB。考虑到通过弯曲柔性基板 [30,31,32,33]、拉长弹性基板 [33,34,35]、利用热膨胀失配 [33、36] 等 [33] 容易引入应变，以及为了通过静电掺杂有效控制自旋极化 [37, 38]，我们还研究了双轴应变和载流子掺杂下的 Mn3Br8 单层。我们的结果表明，在小双轴应变下，随着居里温度的升高，Mn3Br8 单层保持为 FM。另外，双轴应变和载流子掺杂都可以使MAE增加。

计算方法

本研究中的所有计算均采用维也纳ab-initio中实施的自旋极化密度函数理论（DFT）方法进行。 模拟包（VASP）[39]。电子和原子核之间的相互作用由投影增强波 (PAW) 方法描述 [40, 41]，并且电子交换-相关相互作用由广义梯度近似 (GGA) 中的 Perdew-Burke-Ernzerhof (PBE) 函数描述方法[42]。采用哈伯德 U 项来计算强相关相互作用 [43]； 4 eV 的有效现场库仑相互作用参数 (U) 和 1 eV 的交换能 (J) 用于研究 Mn 掺入的 2D 材料，用于 Mn-d 电子 [44]。布里渊区积分是通过采用基于 Monkhorst-Pack 方案的 9 × 9 × 1 k 网格进行的 [45]。声子谱是使用在 VASP 包中实现的 Phonopy 代码 [46] 计算的。沿垂直于单层表面的方向添加 20 Å 的真空空间，以避免相邻层之间的相互作用。平面波基组的截止能量设置为 500 eV。总能量和力的收敛准则设为1 × 10 ^–6 分别为 eV 和 0.01 eV/Å。

结果和讨论

MnBr2 单层的裂解能、基态和稳定性

优化后的 MnBr2 晶格常数为 a =b =3.95 Å，与之前的实验结果一致 (a =b =3.87 Å) [25]。我们首先探讨了从大块 MnBr2 剥离 MnBr2 单层的可行性。图 1a 展示了众所周知、有效且广泛认可的计算裂解能的方法 [47,48,49]。具体而言，解理能是通过计算基态总能量相对于两个断裂部分之间的分离距离 \(d\) 的变化而获得的，如图 1b 所示，a 和 b 的晶格常数为固定为块状 MnBr2 平衡状态下的值。 Grimme 的 DFT-D2 方案 [50, 51] 描述了层间远程 vdW 相互作用。总能量随着分离距离的增加而增加，然后慢慢收敛，如图 1b 所示。计算出的裂解能为 0.10 J/m ² , 与石墨两个断裂部分之间的解理能 (0.35 J/m ² ) [52]，证明了通过微机械剥离法获得MnBr2单层的可行性。

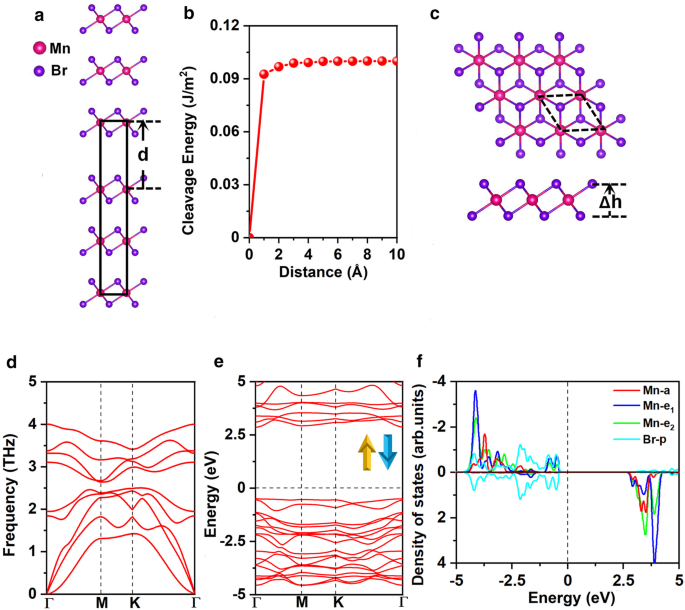
一 用于计算裂解能和b的MnBr2体模型 解理能作为两个断裂部分之间的分离距离 \(d\) 的函数（平衡层间距离设置为 0）。 c 顶视图和侧视图，d 声子谱，e 自旋通道和 f 的电子能带结构 MnBr2 单层的 Mn-d 轨道和 Br-p 轨道的投影态密度 (PDOS)。 Δh 表示两个卤化物平面之间的垂直距离。原始细胞以黑色虚线循环。能带结构和 DOS 的费米能​​级设置为 0 eV

MnBr2 单层具有 \(C_{{{3}v}}\) 对称性，如图 1c 所示；每个Mn原子被6个相邻的Br原子包围，形成一个八面体[MnBr6] ⁴⁻ 单元。如图 2a 和 b 所示，考虑了三种可能的磁性配置，即非磁性 (NM)、铁磁性 (FM) 和反铁磁性 (AFM) 状态。 Mn 离子的高自旋和低自旋状态都被考虑。我们的结果表明，FM 态的 Mn 离子处于低自旋状态，d ¹ 配置，而 AFM 状态的 Mn 离子处于高自旋状态，d ⁵ 配置。 MnBr2 单层的基态是 AFM 态，它比 NM 和 FM 态更稳定，每个配方单位分别稳定 3.91 eV 和 0.72 eV（附加文件 1：表 S1）。 MAE 为 0.25 meV，正值表示易磁化轴沿面外方向，与之前的结果 [16] 一致。优化的晶格常数为a =b =3.95 Å，与块体 MnBr2 的晶格常数相同。 Mn-Br 键长为 2.73 Å，两个卤化物平面之间的垂直距离为 3.03 Å。

a 的示意图 铁磁性和b MnBr2单层反铁磁构型

通过计算形成能、声子谱和弹性常数，进一步研究了 MnBr2 单层的稳定性。形成能计算如下：

其中\(E_{{{\text{MnBr}}}_{{2}} }}\)表示MnBr2单层的能量，\(E_{{{\text{Mn}}}}\)和\(E_ {{{\text{Br}}}}\) 分别是 Mn 和 Br 原子在其体结构中的能量。计算出的 \(E_{{{\text{form}}}}\) 是每个原子 − 1.87 eV；负值意味着形成是放热的，MnBr2 单层是能量有利的。此外，我们计算的 MnBr2 单层声子谱（图 1d）在整个布里渊区中没有显示负频率，表明动态稳定。此外，计算出的弹性常数（附加文件 1：表 S2）符合 \(C_{11}> 0\), \(C_{11} C_{22} - C_{12 }^{2}> 0\) 和 \(C_{66}> 0\)，证实 MnBr2 单层是机械稳定的。计算出的面内刚度为 26.98 J/m ² , 大约 75% 的 MnPSe3 (36 J/m ² ) [49] 和 15% 的 MoS2 单层 (180 J/m ² ) [54]。此外，与 MoS2 单层 (11%) 相比，MnBr2 单层表现出更高的柔韧性和承受更大拉伸应变的能力 [54]。这可能归因于 MnBr2 单层的离子键与 MoS2 单层的共价键。与弹性常数相关的变形分析表明它可以承受其重量（见SI中的详细信息）。

MnBr2 单层的电子能带结构如图 1e 所示，表明 MnBr2 单层是直接带隙为 3.35 eV 的半导体。价带最大值 (VBM) 和导带最小值 (CBM) 都位于 \(\Gamma\) 点。为了深入了解电子结构，Mn-d 和 Br-p 轨道的投影态密度 (DOS) 显示在图 1f 中。 Mn 离子的五个 d 轨道分裂为 \(a(d_{{z^{2} }} )\)、\(e_{1} (d_{xz} + d_{yz} )\) 和 \( e_{2} (d_{xy} + d_{{x^{2} - y^{2} }} )\) 根据 \(C_{{{{3}v}}}\) 对称性分组。更坏的电荷分析表明，每个 Mn 原子向两个相邻的 Br 原子提供两个电子。因此，一个自旋通道中的五个 d 轨道被 Mn ²⁺ 的五个 d 电子完全占据 离子。相应地，两个Mn ²⁺ 晶胞中的离子位于 d ⁵ 磁矩为 5μB/− 5μB 的高自旋态，Br ¹⁻ 离子处于 4p ⁶ 的低自旋状态 具有可忽略的磁矩 - 0.02μB（附加文件 1：图 S1（a））。根据古迪纳夫-金森-安德森 (GKA) 规则，这种配置总是提供反铁磁耦合 [55]。

Mn3Br8 单层的稳定性、电子和磁性能

引入Mn空位以打破d ⁵ Mn ²⁺ 的配置 离子。在 MnBr2 单层的 \(2 \times 2 \times 1\) 超晶胞中引入了单个 Mn 空位，产生了 Mn3Br8 单层。如图 3a 所示，每个 Mn 原子都有四个最近的相邻 Mn 原子并与六个 Br 原子结合，形成一个扭曲的八面体 [MnBr6] 单元。考虑了图 4 中所示的五种磁状态（NM、FM、FIM、AFM-1 和 AFM-2）。我们的结果表明 FM 状态是基态，比其他四种状态分别稳定 9.84 eV、32.90 meV、129.85 meV 和 97.65 meV 每个配方单元。优化后的晶格常数仍为 3.95 Å。与 MnBr2 单层不同，Mn3Br8 单层有 2 种类型的 Mn-Br 键（图 3b）。 Mn 原子和两个中心 Br 原子 (\(d_{{\text{Mn-Br1,2}}}\)) 之间的键为 2.76 Å，而其他 Mn-Br 键 (\(d_{{\text {Mn-Br3,4,5,6}}}\)) 为 2.59 Å。两个卤化物平面之间的垂直距离为 3.33 Å。

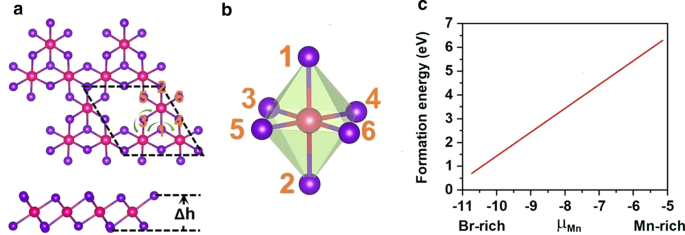
一 Mn3Br8 单层的顶视图和侧视图，\(\Delta h\) 表示两个卤化物平面之间的垂直距离。原始细胞以黑色虚线循环；绿色箭头线显示了超级交易所互动的两条不同路径。 b 扭曲的 MnBr6 八面体的结构。 c 单Mn空位形成能与Mn化学势(μMn)的关系

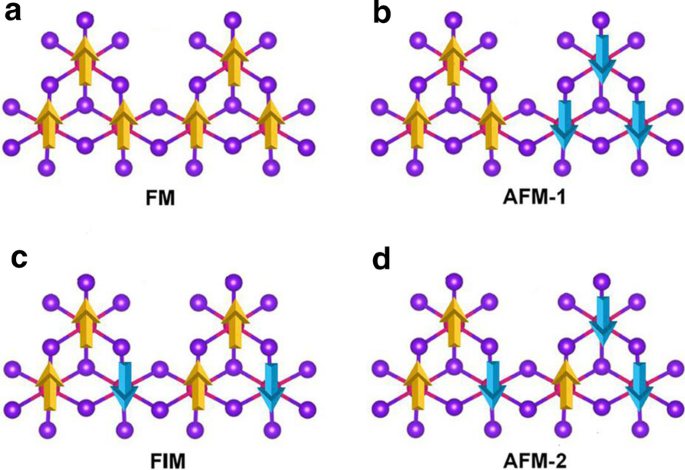
a 的示意图 铁磁性，b antiferromagnetic-1, c 亚铁磁性和d Mn3Br8单层的反铁磁-2构型

为了验证诱导Mn空位的可行性，我们首先通过以下方程计算了富Mn和富Br环境下的空位形成能，

其中 \(E_{{{\text{Mn}}_{{3}} {\text{Br}}_{{8}} }}\) 和 \(E_{{{\text{MnBr}}}_ {{2}} }}\) 代表 Mn3Br8 和 MnBr2 单层的总能量，\(\mu_{{\text{Mn-max}}}\) 是 Mn 在富锰环境下的化学势，即计算为Mn原子在其体结构中的能量，\(\mu_{{\text{Mn-min}}}\)是Mn在富Br环境下的化学势，计算公式为： $$\mu_{{\text{Mn-min}}} =E_{{{\text{MnBr}}}_{{2}} }} - 2 \times \mu_{{\text{Br-max}} }$$

其中 \(\mu_{{\text{Br-max}}}\) 是 Br 的化学势，计算为气相中 Br 原子的能量。如图 3c 所示，在富锰/富溴环境下的形成能量为每个 Mn 空位 6.30/0.71 eV，表明在富溴环境下锰空位的形成在能量上更有利。事实上，已经在 MoS2 单层中通过实验实现了 S 空位 [56]，并且在富含 S 的环境下 S 空位的预测形成能为 2.35 eV [57]。此外，构建像 β-FeOOH/PNGNs（多孔氮掺杂石墨烯网络）这样的多孔纳米结构可以诱导显着的 Fe 空位 [58]，并且采用 Bridgman 方法来诱导有序 Fe 空位。我们也希望这些方法适用于诱导锰空位 [59]。另外，在图 5a 所示的 Mn3Br8 单层的声子谱中没有发现负频率，证明了动力学稳定性。这些结果证实了我们引入Mn空位引入铁磁性的设计。

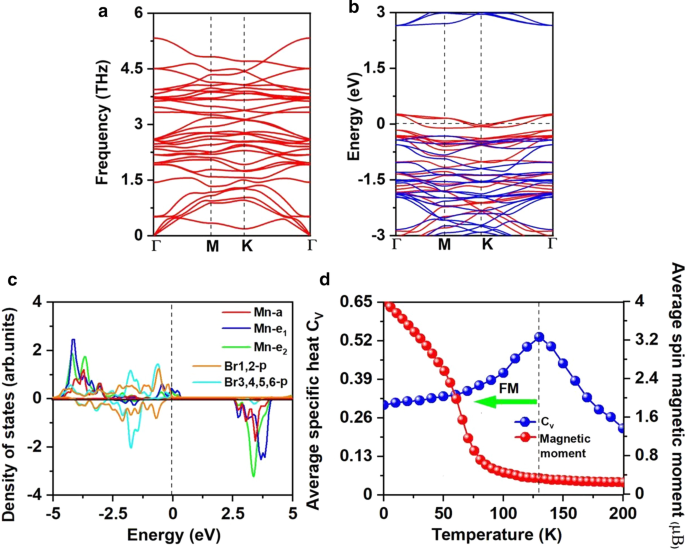
一 声子光谱，b 自旋分辨的电子能带结构，以及 c Mn3Br8 单层的 Mn-d 轨道和 Br-p 轨道的投影态密度 (PDOS)。 d Mn原子的现场磁矩和比热C v 作为基于 Mn3Br8 单层海森堡模型的温度的函数。能带结构和 PDOS 的费米能​​级设置为 0 eV

Mn3Br8 单层的铁磁性归因于 FM 超交换相互作用。根据 Goodenough-Kanamori-Anderson (GKA) 规则 [55]，当 Mn-Br-Mn 角度约为 90°时，Mn 离子之间的超交换相互作用是 FM。在这种配置中（附加文件 1：图 S2），Mn-d 轨道倾向于与不同的正交 Br-p 轨道进行 AFM 耦合，因此间接 Mn-Mn 磁耦合预计为 FM。但是如果每个 Mn 离子有 5 个不成对的电子，如 MnBr2 单层，虽然 Mn-Br-Mn 角接近 90°，但超级交换是 AFM，因为在 MnBr2 单层和自旋中没有空的自旋向上的 Mn-d 轨道up d 电子不能在相邻的 Mn 位点之间跳跃 [60]。 Mn3Br8 中存在两种不同的超交换相互作用路径（图 3a），并且都是 FM。一个涉及中心 Br1,2 原子，Mn-Br 键长为 2.76 Å，Mn-Br-Mn 角为 87.5°；另一个涉及 Br3,4,5,6 原子，Mn-Br 键长为 2.59 Å，Mn-Br-Mn 角为 95°。 Br3,4,5,6 原子的 p 轨道和 Mn-d 轨道之间的杂化相互作用强于涉及 Br1,2 原子的 p-d 杂化相互作用，如图 5c 所示，特别是从 - 2 eV 到 - 1.4 eV。虽然从 1.4 到 − 0.9 eV，p -d Br1,2原子杂化占主导。

更坏的电荷分析表明，每个 Mn 原子向相邻的 Br 原子提供 8/3 的电子。因此，Mn 离子位于 Mn ^8/3+ 状态。如图 5c 所示，每个 Mn 离子的 13/3 电子都填充在 d 轨道的自旋向上通道中，而 Br ¹⁻ 离子处于 4p ⁶ 的低自旋状态 .因此，每个Mn ^8/3+ 的磁矩 离子为13/3μB； Br ¹⁻ 的磁矩 离子是可以忽略的（附加文件 1：图 S1(b)）。对于 d ⁰ 也可以观察到由空位引起的铁磁性 系统，如 ZnS 和 ZnO [61, 62]，单个空位可以引起高达 2μB 的磁矩 [61]。对于每个 Mn 离子，2/3 d-轨道未被占据； \(e_{1}\) 和 \(e_{{2}}\) 轨道的自旋通道被部分占据并穿过费米能级，导致半金属性。从图 5b 所示的自旋分辨电子能带结构中也可以观察到半金属特征。自旋向上通道是金属的，而自旋向下通道是半导体，间接带隙为 2.97 eV； VBM/CBM 位于 \({\text{M}}\)/\(\Gamma\) 点。带隙值接近于 MnP (2.86 eV) [63]、MnAs (2.92 eV) [63] 和 Ni2NO2 (2.98 eV) [64]，这足以阻止热激发自旋-翻动。与 MnBr2 单层相比，半导体通道的 VBM 和 CBM 都更接近费米能级。 CBM 仍以 Mn 原子为主，而 VBM 以新的 Br1,2 原子为主。同时，半导体通道由直接变为间接，带隙减小。在具有H官能化的MnCl2单分子层中也观察到了类似的现象[60]。

磁化方向由磁各向异性能 (MAE) 决定。固体的 MAE 来自两个贡献者，即与自旋轨道耦合 (SOC) 相关的磁晶能 (MCE) 和由静磁偶极-偶极相互作用引起的磁偶极各向异性能 (MDE)。 3D 各向同性材料（如 bcc Fe 和 fcc Ni）中的 MDE 非常小。但对于由具有大磁矩的过渡金属原子组成的低维材料，MDE 不容忽视 [65,66,67]。 MCE 定义为通过考虑 SOC 沿面内（100 或 010）和面外（001）方向的磁化能量之间的差异。 MDE 是作为平面内和平面外磁化强度之间的 \(E_{d}\) 之差获得的。 \(E_{d}\) 在原子里德堡单位中由 [65, 66]

其中光速，\(c =274.072\)，\(i/j\) 是晶胞中的原子位置向量，而\({m}_{i}/{m}_{j}\ ) 是站点 \(i/j\) 上的原子磁矩 (μB)。磁偶极马德隆常数\(M_{ij}\)通过

其中 \(R\) 是晶格向量。在二维材料中，由于所有的 \(R\) 和 \(i\) 都在平面内，所以平面外磁化的第二项为零，导致正的 \(M_{ij}\ )，而 \(M_{ij}\) 对于面内磁化强度为负值 [67]。因此，MDE与过渡金属的磁矩有关，总是偏向于面内磁化。

Mn3Br8 单层的计算 MCE 为每分子式单位 - 1.90 meV（图 6a），远大于块状 Fe（每个原子 0.001 meV）和 Ni（每个原子 0.003 meV）[68]，并且大于Rh (111) 上的 Fe 单层（每个原子 0.08 meV）[69]，表明 Mn3Br8 单层的磁化强度是热稳定的。 MCE与方位角的关系可用下式[70]表示：

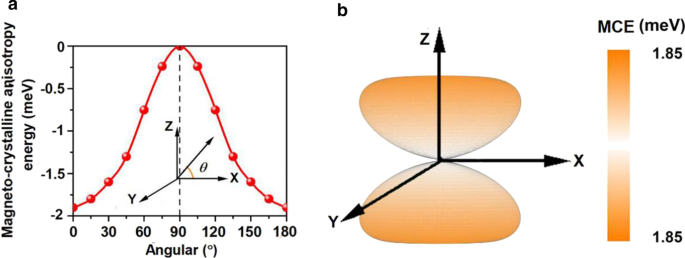
磁晶各向异性能 (MCE) a 的变化 关于方位角和 b 在Mn3Br8单层空间中

其中\(A\) 和\(B\) 是各向异性常数，\(\theta\) 是方位角。拟合结果见附加文件1：图。 S3.此外，自旋轴在整个空间中旋转时 MCE 的演变如图 6b 所示。 xy 平面内的 MCE 没有差异，但沿垂直于 xy 平面的方向达到最大值，证实了强磁各向异性。 MDE 为每分子式单位 - 0.43 meV，而 MAE (MCE + MDE) 为每分子式单位 - 2.33 meV。负值表示易磁化轴沿面内方向。 MDE 不会改变磁化方向，但会增强磁化方向。此外，Mn3Br8 单层的 MAE 远大于 MnBr2 单层的 MAE，再次证明了我们设计的有效性。

我们通过执行基于海森堡模型的蒙特卡罗 (MC) 模拟进一步计算了 FM Mn3Br8 单层的 \(T_{c}\)，这已被证明是预测 \(T_{c}\) 的有效方法对于二维材料 [11, 15, 48, 58, 71,72,73,74,75,76]。我们估计的 CrI3 单层 \(T_{c}\) 为 42 K（附加文件 1：图 S4）[76]，与实验测量值 [2] 和先前的计算结果 [15, 58, 71, 72, 74, 76]，这证明了我们采用的方法的准确性。包括最近邻（NN）磁相互作用的自旋哈密顿量描述为

其中\(J\)是NN磁交换参数，\(M_{i/j}\)是Mn离子的磁矩和基于蒙特卡罗方法的接近自旋极化电子数的积分[71, 77 , 78], \(i\) 和 \(j\) 代表 NN 对 Mn 离子。磁耦合参数\(J\)通过FM和AFM状态之间的能量差计算为

NN Mn 离子的计算 \(J\) 为 1.01 meV；正值表示偏好调频耦合。

采用计算出的 NN Mn 离子的 \(J\) 和包含 20,000 个磁矩矢量的 \(100 \times 100 \times 1\) 超级单元来执行 MC 模拟。每个温度的模拟持续10 ⁵ 脚步。每个磁矩矢量在所有方向上随机旋转。图 5d 显示了定义为 \(C_{{_{V} }} ={{\left( {\left\langle {E^{2} } \right\rangle - \left\langle E \ right\rangle^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {\left\langle {E^{2} } \right\rangle - \left\langle E \right \rangle^{2} } \right)} {K_{B} T^{2} }}} \right. \kern-\nulldelimiterspace} {K_{B} T^{2} }}\) 与温度，从中我们通过定位 \(C_{v}\) 的峰值位置，获得了 Mn3Br8 单层的 130 K 的 \(T_{c}\)，高于液氮温度 (77 K) 和 \(T_ {c}\) 的 CrI3 (45 K) [2] 和 Cr2Ge2Te6 (28 K) [3], CrX3 (X =F, Cl, Br) (36 ~ 51 K) [11], CrXTe3 (X =Si, Ge) (35.7 K, 57,2 K) [48]。我们的计算表明，FM Mn3Br8 单层具有比液氮温度高的大 MAE 和居里温度。

双轴应变和载流子掺杂下的Mn3Br8单层

应变工程已被证明适用于许多 2D 材料，并且可以有效地改变结构参数，例如键长和角度，以及调整电子和磁性。在这种情况下，我们在- 5% 到 5% 的双轴应变下研究了 Mn3Br8 单层。结果表明，Mn3Br8 单层在- 5 到 5% 的双轴应变下保持为 FM，原子磁矩几乎没有变化。如图所示。如图 7a 和 c 所示，两个 Mn 原子与 Br1,2 原子（θMn-Br1,2-Mn）之间的夹角为 84°–90°，随着应变逐渐增大并逐渐接近 90°。涉及 Br3,4,5,6 原子（θMn-Br3,4,5,6-Mn）的 Mn-Br-Mn 角逐渐偏离 90°，范围从 90° 到 100°。因此，通过不同正交Br-p轨道介导的Mn离子之间的超交换相互作用仍然是FM。

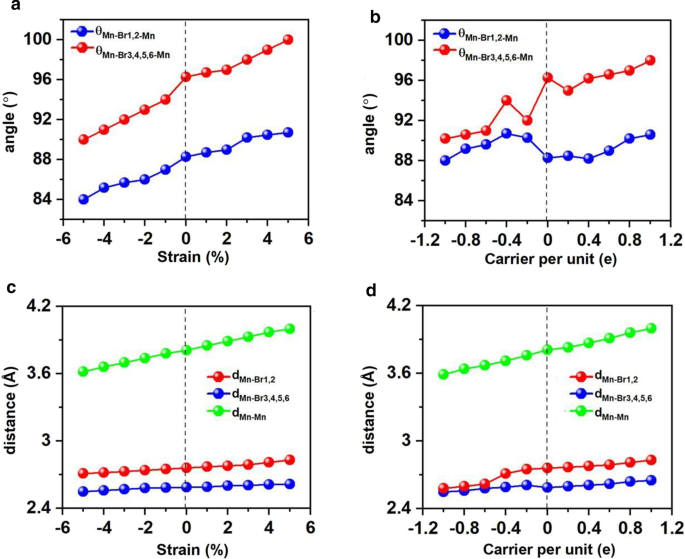
两个 Mn 和 Br 原子之间的角度、Mn 和 Br 原子之间的距离以及最近的相邻 Mn 原子之间的距离相对于施加的双轴应变和载流子掺杂的变化。 a 的变体 角度和 c 相对于双轴应变的距离，b 的变化 角度和 d 载流子掺杂的距离。载流子掺杂的正负值分别代表电子和空穴的掺杂

随着应变从 –5% 变为 5%，Mn-Mn 和 Mn-Br 距离均单调增加。相应地，图 8a 所示的双轴应变下的交换参数随着双轴应变从 –5% 变为 5% 而减小，并在 –5% 双轴应变下达到最大值 (1.18 meV)。 Mn3Br8 单层在 –5% 双轴应变下的居里温度为 160 K（图 9a）。特别是在拉伸应变增加的情况下，Mn-Br键变长，Mn-Br3,4,5,6-Mn的角度偏离90°，这是FM超交换相互作用变弱的主要原因。因此，居里温度降低。它类似于 CrPTe3 和 FePS3 单层 [79]。此外，MDE 随着应变的增加而降低（附加文件 1：图 S5（b））； –1% 双轴应变下的 MAE 最大 (–3.04 meV)。 –5-5% 的应变不会对 Mn3Br8 单层造成大的结构变形，其能带结构的形貌几乎没有变化。 Mn3Br8 单层保持半金属。半导体自旋通道中的 VBM 和 CBM 都略微向上移动到更高的能量，如图 1 和图 3 所示。 8c 和 10；在5%双轴应变下，带隙随着双轴应变增加至3.12 eV而缓慢增加。

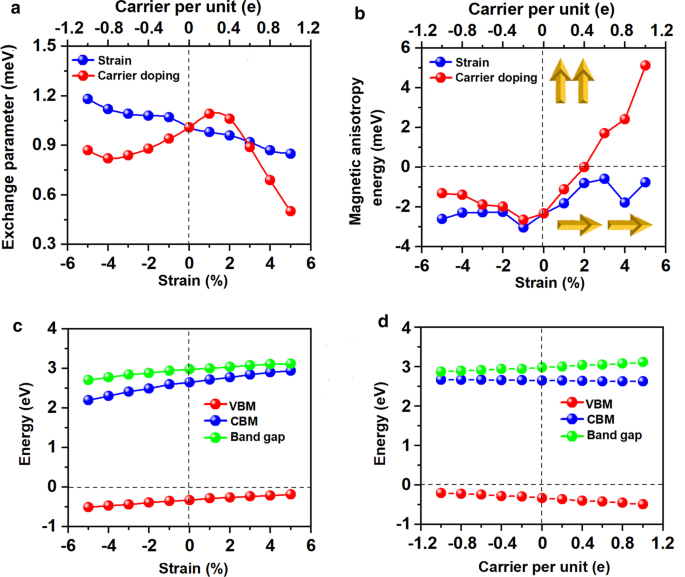
a 的变体 交换参数和 b Mn3Br8 单层的磁各向异性能 (MAE) 与施加的双轴应变和载流子掺杂有关。 The variations of valence band maximum (VBM), conduction band minimum (CBM), and band gap in the semiconducting channel for Mn3Br8 monolayer with respect to c the applied biaxial strain and d carrier doping ranging. Positive and negative values of the carrier doping represent the electron and hole doping, respectively

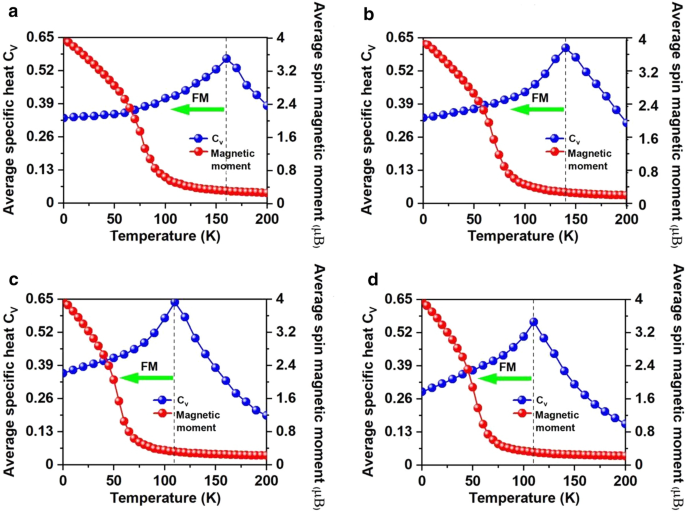
On-site magnetic moments of Mn atoms and the specific heat C v as function of temperature based on Heisenberg model for Mn3Br8 monolayer a under -5% biaxial strain, with b 0.2e, c -0.6e, and d -0.8e carrier doping per formula unit. Positive and negative values represent the electron and hole doping, respectively

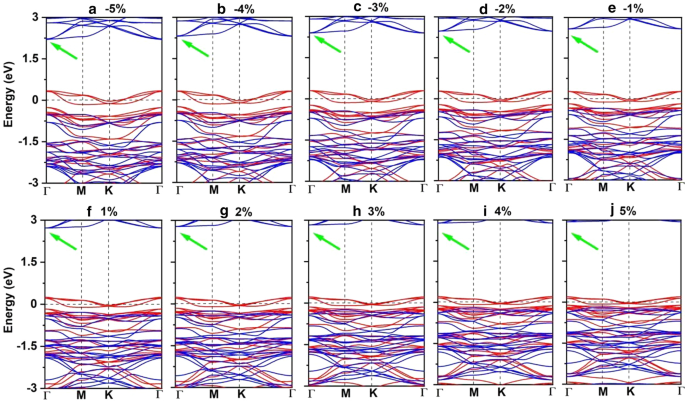
一 –j Spin-resolved band structure for Mn3Br8 monolayer under biaxial strain from -5% to 5%. The green arrow denotes the indirect band gap

Electron/hole doping always leads to VBM/CBM moving away from the Fermi level. Our calculations show that Mn3Br8 monolayer with –1–1e (~ \(1.7 \times 10^{14} {\text{cm}}^{{ - 2}}\)) carrier doping per formula unit is still FM; the atomic magnetic moment of each Mn ion is still 13/3μB. As shown in Fig. 7b and d, with carrier doping from –1e to 1e per formula unit, the Mn-Br-Mn angles involving Br3,4,5,6 atoms are about 90° ~ 98°; the Mn-Br1,2-Mn angles are about 88° ~ 90°. The Mn–Mn and Mn-Br1,2 distances increase with the increasing electron doping. Mn3Br8 monolayer with 0.2e and 0.4e carrier doping has larger magnetic exchange parameter (Fig. 8a). The Curie temperature at 0.2e electron doping is largest of 140 K (Fig. 9b). Additionally, with –1e ~ 0.2e doping, the MAE is along in-plane directions; the MDE decreases with the increasing electron doping. Under 0.4e doping, the MCE turns to be positive with the value of 0.41 meV per formula unit; the MAE is only 0.01 meV per formula unit with taking the MDE into account (Additional file 1:Figs. S5(a) and (b)). With 0.6e, 0.8e and 1e doping, the PMA (perpendicular magnetic anisotropy energy) is 1.70, 2.42, and 5.13 meV, respectively, large enough for spintronic applications (Fig. 8b).

Additionally, Mn3Br8 monolayer with carrier doping of –1e ~ 1e per formula unit maintains to be half-metallic. Its band gap in the semiconducting spin-channel increases/decreases slightly with the increasing electron/hole doping as shown in Fig. 8d; the positions of the VBM and CBM do not change. Exceptional, Mn3Br8 monolayer turns to be FM spin-gapless semiconductors (SGS) with the metallic spin-channel opening up a very small energy gap (0.07 eV) under –0.6e and –0.8e hole doping; its Fermi level locates in the band gap region (Fig. 11b and c, more clearly figures are presented in Additional file 1:Figs. S6(a) and (b)). Correspondingly, electrons may be easily excited from the valence band to the conduction band with a small input of energy, which simultaneously produces 100% spin polarized electron and hole carriers. The Curie temperature at –0.6e and –0.8e hole doping is 110 K (Fig. 9c and d), higher than liquid-nitrogen temperature (77 K). Considering with that the charge density modulation of \(10^{13} \sim10^{15} {\text{cm}}^{ - 2}\) was already achieved experimentally [80,81,82], our predicted properties of Mn3Br8 monolayer with carrier doping are also experimentally approachable.

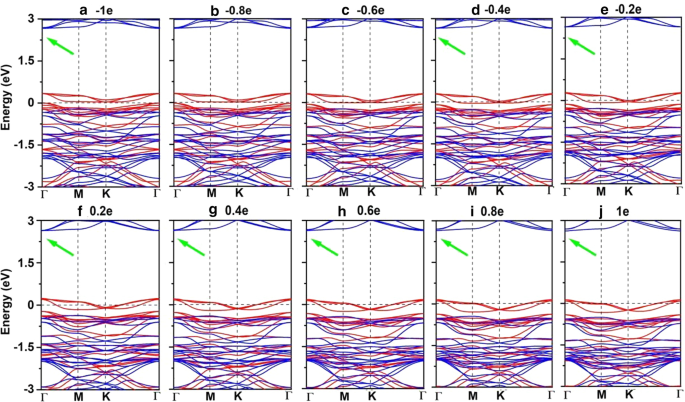
一 –j Spin-resolved band structure for Mn3Br8 monolayer with carrier doping from -1e to 1e per formula unit. Positive and negative values represent the electron and hole doping, respectively. The green arrow denotes the indirect band gap

结论

In summary, the stability, electronic, and magnetic properties of Mn3Br8 monolayer have been carefully investigated. Our results show that Mn3Br8 monolayer is FM half-metal with 130 K Curie temperature and with 2.97 eV band gap for the semiconducting spin-channel. Plus, the magnetic moment of each Mn ion is 13/3μB; the MAE is –2.33 meV per formula unit. The Mn3Br8 monolayer is designed by inducing single Mn vacancy in the \({2} \times {2} \times {1}\) supercell of MnBr2 monolayer to break the AFM coupling d ⁵ 配置。 The feasibility of forming the Mn vacancy and the dynamical, mechanical stability of Mn3Br8 monolayer have been comprehensively confirmed. Additionally, Mn3Br8 monolayer under biaxial strain –5% ~ 5% is still FM half-metal with 2.71 ~ 3.12 eV band gap for the semiconducting spin-channel, whose Curie temperature under –5% biaxial strain is 160 K. Both biaxial strain and carrier doping make the MAE increase, which turns to be perpendicular to the plane under electron doping. With 0.8e and 0.6e hole doping, Mn3Br8 monolayer turns to be spin-gapless semiconductor (SGS) with band gap of 0.07 eV. Our calculations demonstrate Mn3Br8 monolayer as FM half-metal with high Curie temperature, and having large MAE and large magnetic moment, and tunable electronic and magnetic properties under the applied biaxial strain and carrier doping.

数据和材料的可用性

在当前研究期间生成和/或分析的数据集可根据合理要求从相应作者处获得。

缩写

二维：

二维

原子力显微镜：

Antiferromagnetic

CBM：

导带最小值

DFT：

密度泛函理论

DOS：

态密度

FIM:

Ferrimagnetic

调频：

Ferromagnetic

GGA：

广义梯度逼近

GKA:

Goodenough–Kanamori–Anderson

MAE:

Magnetic anisotropy energy

MCE:

Magneto-crystalline anisotropy energy

MC:

Monte Carlo

MDE:

Magnetic dipolar anisotropy energy

MTJ:

Magnetic tunneling junctions

NM:

Non-magnetic

NN:

Nearest neighboring

爪子：

投影仪增强波

PBE：

Perdew–Burke–Ernzerhof

PMA：

Perpendicular magnetic anisotropy energy

PNGN:

Porous nitrogen-doped graphene networks

SGS:

Spin-gapless semiconductor

SOC：

Spin–orbit coupling

VASP：

Vienna ab-initio simulation package

VBM：

价带最大值

VDW:

范德华