形态和晶体结构对二氧化钛纳米管热导率的影响

背景

由于电子设备和纳米机电系统 (NEMS) 的持续小型化，纳米结构及其性能的研究在过去几年引起了广泛关注 [1, 2]。控制纳米结构的尺寸和成核的研究之前已经提出，因为纳米结构已被用于不同的潜在应用 [3, 4]。由于纳米结构在电子工业、NEMS 和先进热电领域的应用，通过控制尺寸、成分和结构来控制纳米结构中的热性能的研究特别令人感兴趣 [2, 5, 6]。一种特殊情况是尽量减少集成电路 (IC) 的热耗散，以保证其稳定性和长寿命。

一维 (1D) 材料，例如碳纳米管 (CNT)，室温热导率为 3000 W m ^-1 K ⁻¹ ，远高于金刚石晶体 [2, 5]。碳纳米管是石墨烯的无缝轧制板，由于碳-碳键强且没有点缺陷和边界，因此具有更高的热导率[6]。与碳纳米管相反，与大块材料相比，其他一维晶体半导体显着降低了热传输[6]。低维纳米结构中热导率的降低归因于声子平均自由程 (MFP) 的减少、小晶粒尺寸、声子边界散射、粗糙度和点缺陷 [6,7,8]。

硅纳米线已被研究用于定制热传输以用于热电应用。首次，Li 等人。 [9] 报道称，由于声子边界散射，硅纳米线的热导率比体硅低两倍。直径为 50 nm 的硅纳米线的热导率接近硅的非晶极限，与体硅相比，热导率降低了 100 倍 [10]。这些具有显着降低的热导率和增加的电导率的硅纳米线具有更高的热电效率 [10,11,12,13]。还报告了其他纳米线与其体材料相比降低的热性能，例如 Bi2Te3 [14, 15]、Si/SiGe [16]、Ge/SiGe [17, 18]、ZnTe [19]、GaN [20] 、InSb [21]、CdS [22]、PbS、PbSe [23]、InAs [24]、Bi [25]、SrTiO3 [26]、ZnO [27] 和 TiO2 纳米线 [28, 29]。此外，还报道了对纳米管的热研究，如 Si [30]、Bi2Te3 [31] 和 TiO2 纳米管 [1, 32,33,34]。基于这些研究，可以得出结论，由于纳米管壁内的额外声子散射，纳米管的热导率低于相应纳米线的热导率 [31]。应该注意的是，结晶纳米管的热导率通常高于非晶纳米管的热导率，并且受其表面粗糙度的影响很大 [32, 34]。此外，温格特等人。 [30] 注意到结晶硅纳米管的热导率低于其非晶等效物。这种对结晶硅纳米管中超出非晶极限的热导率的观察归因于弹性软化和强声子边界散射 [30]。非晶纳米材料中的热传输主要 (93%) 归因于扩散子（非传播“扩散子”模式），而其余 4% 与称为“传播体”的类声子模式有关，3% 与局域模式有关称为“位置”[35]。由于扩散子的平均自由程通常被认为是原子间距离的自由程，因此预计非晶纳米结构的热导率与尺寸无关[36]。

Cahill 和 Pohl 为无序材料提出了一个众所周知的最小热导率模型 [37]。根据该模型，二氧化钛的建议最小热导率（非晶极限）为 1.6 W m ⁻¹ K ⁻¹ [38]。没有报道过非晶氧化物的热导率随尺寸而降低[35]，尽管一些氧化物薄膜的热导率低于非晶极限。获得较低的热导率值的原因是结构中的杂质或薄膜与基板之间的热边界电阻[35]。

二氧化钛纳米管——具有高比表面积的一维纳米结构——已被设计用于许多潜在的应用[39]。二氧化钛纳米管可以通过各种方法合成，包括水热 [40] 和电化学阳极氧化 [39, 40]、化学处理 [41]、快速击穿阳极氧化 (RBA) [42] 以及模板辅助和静电纺丝方法 [40]。热导率范围为 0.40–0.84 W m ⁻¹ K ⁻¹ [1] 和 0.55–0.75 W m ⁻¹ K ⁻¹ [33] 已经观察到通过水热法合成的钛酸盐纳米管。布拉米等人。 [32] 报道了 0.85 W m ⁻¹ 的热导率 K ⁻¹ 对于单个无定形纳米管和 1.5 W m ⁻¹ K ⁻¹ 用于电化学阳极氧化制备的锐钛矿型二氧化钛纳米管。另一方面，据报道分离的二氧化钛纳米管阵列的热导率为 0.617 W m ^-1 K ⁻¹ 沿管方向为无定形和 1.12 W m ⁻¹ K ⁻¹ 对于锐钛矿纳米管 [34]。交叉管非晶热导率为 0.077–0.1024 W m ^-1 K ⁻¹ 对于无定形纳米管和 0.24 W m ⁻¹ K ⁻¹ 在结晶纳米管的情况下[34]。这些报告中的二氧化钛纳米管阵列是通过电化学阳极氧化方法在 Ti 基板上生长的，使用具有氟离子的有机电解质（第三代 TNT），壁厚为 30-70 nm [32] 和 15 nm [34]。 RBA制备的纳米管包括第四代TNTs[43]，其中利用无氟电解质获得成束的二氧化钛纳米管[42]。

在目前的贡献中，我们报告了具有可变形态、晶体结构和壁厚低于 30 nm 的二氧化钛纳米管的热导率的比较实验研究。纳米管是通过化学加工 [41] 和 RBA [42] 合成的。导热系数的研究扩展到第四代二氧化钛纳米管（即RBA制备的粉末）以及不同合成方法制备的TNT粉末的比较。 Liang 和 Li [44] 提出了一种纳米材料尺寸相关热导率的分析模型，这在纳米线和薄膜中得到了实验证实。该模型后来由 Gao 和 Jelle [1] 针对纳米管进行了修改，但尚未经过实验验证。根据该模型，纳米管的热导率取决于壁厚 [1]。布拉米等人。 [32] 研究了壁厚为 30-70 nm 的 TNT 的热导率；然而，在他们的研究中没有观察到热导率随壁厚的降低。在本报告中，我们通过减少结晶二氧化钛纳米管的壁尺寸，通过实验验证了二氧化钛纳米管的尺寸依赖性热导率。与普遍看法相反，目前的数据与文献中的数据相结合，表明非晶二氧化钛纳米管的热导率也随尺寸而降低。

方法/实验

TNT 合成

二氧化钛纳米管 (TNT) 粉末是通过分别在 [41, 42] 中详细讨论的化学处理和快速分解阳极氧化 (RBA) 方法制备的。制备了三种具有不同晶体结构和形态的二氧化钛纳米管，即（i）多壁开放式 TNT，（ii）一端开口另一端封闭的无定形单壁 TNT，以及（iii）结晶二氧化钛纳米管一端打开，另一端关闭。多壁开放式二氧化钛纳米管采用化学加工方法制备，具有钛酸盐（Nax H2 − x Ti3O7·nH2O，其中 0 <x <2) 具有锐钛矿相 [41] 的突出峰，并在全文中称为 TNTA,T。其他两种类型的纳米管是通过 RBA 方法制备的，要么使用水基电解质（0.1 M 高氯酸）获得具有锐钛矿结构的结晶 TNT，要么使用有机电解质（乙二醇 + 水 + 高氯酸）制备无定形纳米管 [42] . RBA生产的无定形（TNTAmor）和结晶（TNTA）二氧化钛纳米管粉末是单壁的，一端开口另一端封闭。这些 TNT 的示意图如图 1 所示。

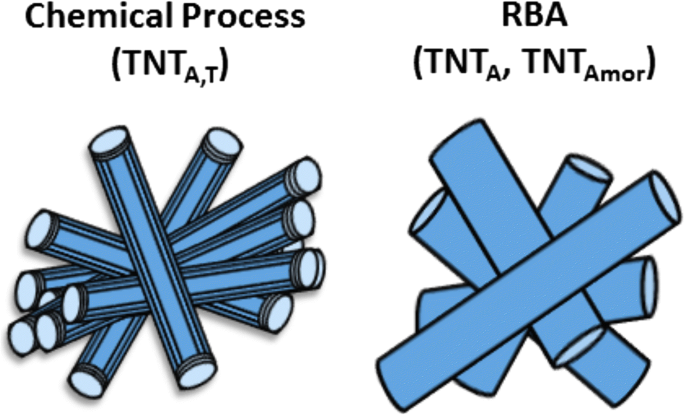
TNTA、T、TNTA、TNTAmor示意图

表征方法

使用透射电子显微镜（TEM；Tecnai F-20 G2 200 kV FEG S-twin GIF）在 200 kV 的操作电压下检查二氧化钛纳米管粉末的形态和尺寸。通过使用X射线衍射（XRD）获得晶体结构。 XRD 数据是通过使用帕纳科 X’pert Pro 衍射仪获得的。工作波长为 0.154 nm Cu-Kα 辐射，电压和电流分别为 40 kV 和 45 mA。每种粉末的密度通过比重瓶（Upyc 1200e v5.04；Quantachrome Corporation）测量。然后将粉末压缩成 10 毫米的小球，用于热导率测量。颗粒是通过纳米管粉末的静水压制成的，所得颗粒的厚度在 2-4 毫米范围内。测量的颗粒厚度和计算的密度与施加的压力有关，压力控制在 5 到 50 kN 的范围内以调整每个颗粒的密度。用场发射枪扫描电子显微镜（FEG-SEM；Hitachi S-4700）分析丸粒表面。

在室温下，使用带有 Proteus LFA 软件的 Netzsch LFA 467 设备，通过使用闪光法测量丸粒的热扩散率。短光氙激光脉冲加热小球的后表面。在测量之前，颗粒涂有石墨喷雾以改善热辐射的吸收和发射。红外探测器观察到颗粒另一侧的相应温度变化。根据帕克等人的说法。 [45] 根据实验数据，可以使用以下关系式获得热扩散率：

这里，α 是样品的热扩散率，d 是样品厚度，t ^1/2 是半信号高度处的时间值。每个样品重复 LFA 测量五次。 Proteus 软件用于拟合测量。样品的热导率由下式[45]求得：

在这里，κ 表示热导率，α 表示热扩散率，c p 是比热容，ρ 是密度值。二氧化钛纳米管的比热容在 100 K 以上接近块状二氧化钛的比热容 [46]，因此，二氧化钛纳米管的比热容值来自郭等人的研究。 [34, 47]。颗粒的密度由颗粒的重量和相应的体积计算。实验结果的不确定性来自于扩散率测量的 LFA 测量单元 (2%) 和颗粒厚度计算的误差（千分尺）。热导率实验的总误差估计为8%。

结果与讨论

纳米管晶体结构的 XRD 数据如图 2 所示。TNTAmor 数据没有峰，证实了通过 RBA 利用有机电解质制备的纳米管的无定形结构 [42]。化学加工的纳米管 (TNTA,T) 显示出锐钛矿相的显着峰以及 H2Ti3O7 峰。锐钛矿以外的结构被指定为 Nax H2 − x Ti3O7·nH2O 其中 0 <x <2，如先前研究中所述[41]。水基电解液制备的TNTA具有锐钛矿峰。从XRD数据可以看出，两种纳米管是结晶型的，一种是非晶型的。

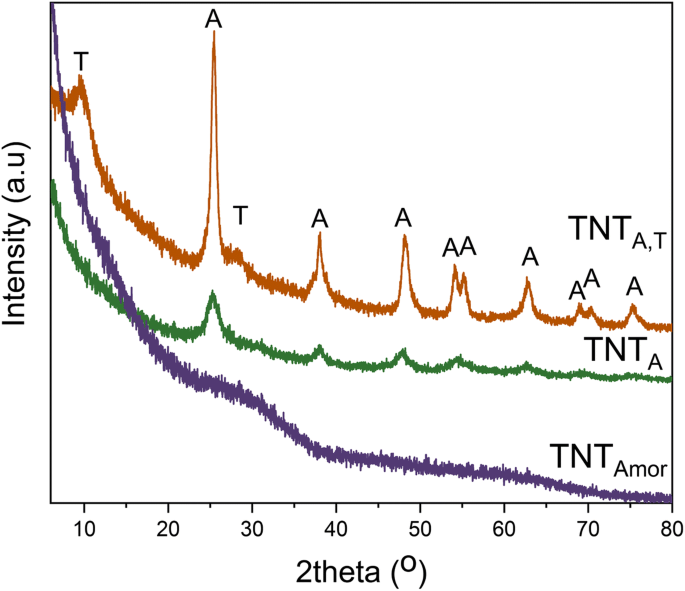
由锐钛矿 (TNTA)、钛酸盐和锐钛矿 (TNTA,T) 和无定形结构 (TNTAmor) 组成的结晶二氧化钛纳米管的 XRD [41, 42]。 T =H2Ti3O7，A =锐钛矿峰

通过化学加工方法合成的二氧化钛纳米管是多壁的，这是由于纳米管合成过程中纳米片的滚动[48]。这些开放式纳米管的壁厚为 4-5 纳米，长度从 60 到数百纳米不等 [41]。来自这些纳米管的 TEM 图像显示在图 3a、b 中。如图 3a 所示，纳米管是随机取向的，更喜欢保持成束状。 3 到 4 层多层结构很明显，如图 3b 所示。 RBA 生产的结晶纳米管壁厚在 7-12 nm 范围内，长度为 18-35-μm [42]（表 1）。它们是单壁的，一端开放，另一端封闭，如图 3c 中的显微照片所示，其中插图显示了开放端。由 RBA 制备的无定形纳米管与由 RBA 方法制备的结晶纳米管具有相似的形态。然而，由于电解质的贡献，尺寸是不同的。壁厚在 15-30 nm 范围内，管长在 6-13 μm 范围内 [42]。图 3d 显示了单壁非晶纳米管的 TEM 图像。粗糙度是 TNT 壁面高度偏离参考平面的平均值 [44]。从 TNT 的 TEM 图像估计的平均粗糙度值对于 TNTA,T 约为 0.3 nm，对于 TNTA 约为 1.0 nm，对于 TNTAmor 约为 1.5 nm。

a 的 TEM 图像 TNTA,T 化学加工制备，b 显示多壁纳米管结构的 HR-TEM 显微照片，c RBA制备的单壁结晶纳米管（TNTA）和d 非晶纳米管（TNTAmor）

使用液压机将二氧化钛纳米管颗粒制备成不同的密度和相应的孔隙率。 TNTAmor 粉末以 20 kN 的最大载荷压实，因为在较高载荷下无法获得 LFA 测量所需的颗粒光滑表面。颗粒的孔隙率通过以下公式计算（方程 1）：

其中 ρ o 是散装样品的密度，它是通过比重瓶测量获得的粉末密度，如表 1 所示。ρ 是颗粒的计算密度和 P 是样品的孔隙率。在附加文件 1 中使用 FESEM 研究了颗粒的表面。表面分析显示纳米管束在表面上随机取向（附加文件 1：图 S1），即可以在不同方向（开口顶部，关闭底部和侧视图位置）在附加文件 1：图 S1。来自 TNTA、TNTAmor 和 TNTA,T 颗粒的颗粒表面的类似 SEM 图像在附加文件 1 中描述：图 S2a-c。通过 LFA 方法测量的热扩散率总结在表 2 中。测量的热导率被绘制为孔隙率的函数，如图 4 所示。测量的热导率随着所有样品的孔隙率增加而降低（表 2）。 Gao 和 Jelle 获得了具有不同颗粒孔隙率的样品的热导率值的相似趋势 [1]。与块状二氧化钛 (8.5 W m ^-1 ) 相比，纳米管的热导率明显降低 K ⁻¹ [34]）。一维二氧化钛纳米管中导热率的这种抑制归因于由于尺寸减小而导致的声子限制和声子边界散射 [1]。由于纳米管随机排列并压实以形成颗粒，因此它们也相互连接。在这种情况下，纳米管和 Kapitza 电阻之间互连区域的声子散射也会影响整体热导率值。然而，为简单起见，这里忽略了考虑纳米管取向的接触卡皮察电阻和声子边界散射。

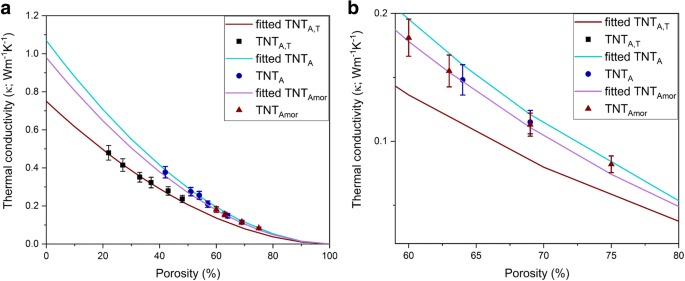
一 测量二氧化钛纳米管（符号）与孔隙率的有效热导率。实线表示使用形状因子为 1.24 的有效热导率模型（方程 6）进行拟合。 b 为清晰起见，60-80% 孔隙率范围内的热导率

考虑到二氧化钛纳米管和充满空气的孔隙，样品的测量热导率估计了纳米管颗粒的电导率。空气的热导率假定为 0.026 W m ⁻¹ K ⁻¹ [1]。纳米管的热导率 (κ TNTs) 排除孔隙率的影响可以通过使用方程给出的有效热导率模型进行估计。 4 [1, 49]，对于非导电孔的情况，其简化为方程式。 5 [1]：

其中 κ eff 是包括孔隙率效应的有效热导率，κ air 是空气的热导率，P 是孔隙率。 TNTA,T 的热导率由等式估计。 4 在 0.44–0.61 W m ⁻¹ 的范围内 K ⁻¹ 对于 TNTA,T。使用有效热导率模型（方程 4），具有大致相似尺寸的纯钛酸盐纳米管的热导率已报告为 0.40–0.84 W m ^-1 K ⁻¹ [1]。当使用相同的有效热导率模型（方程 4）时，我们的结果与报告的值非常吻合。

然而，纳米管压块中的气隙形状只是部分随机的，因为管本身具有非随机形状。为了说明孔隙的不同形状，Bauer [49] 在求解拉普拉斯热传导方程的基础上推导出了适用于全范围孔隙度的分析模型。该等式可以表示为以下形式：

在这个方程中，ε 是与孔隙形状相关的形状因子或校正因子。它的值说明了孔隙的可变形状。对于气隙的随机形状，ε 是 2/3 [1, 27, 50] 从而减少方程。 5 等式。 6.

Yang等人已经估计了多面体形状的形状因子值。 [50]，基于 1 到 1.48 之间的建模形状因子。当我们的数据拟合方程时。 6，最佳拟合（见图 4）是为形状因子 ε 获得的 值为 1.24。根据拟合，发现 TNTA 的热导率为 1.07 W m ⁻¹ K ⁻¹ .该值略低于之前报告的值 1.12 W m ⁻¹ K ⁻¹ 对于锐钛矿纳米管阵列 [34] 和 1.5 W m ^{− 1} K ^{− 1} 对于单个锐钛矿纳米管 [32]。相应地，发现 TNTAmor 的热导率为 0.98 W m ⁻¹ K ⁻¹ .与 TNTA 相比，非晶纳米管的导热系数略低是由于它们的非晶结构。 [32, 34] 还报道了非晶二氧化钛纳米管的热导率值低于结晶纳米管的热导率值。通常，与晶体材料相比，已知非晶薄膜和材料具有较低的热导率，尽管在如此小的规模下，其他因素也会影响热导率值。例如，温格特等人。 [30] 报道称，与具有相似尺寸的无定形对应物相比，结晶硅纳米管的热导率低 30%。这些纳米管的亚非晶热导率归因于结晶纳米管中的强弹性软化效应[30]。与非晶薄膜相比，通过 ALD 工艺沉积的 100-nm 非晶二氧化钛薄膜的实测热导率为 1.29 W m ^-1 K ⁻¹ [47]。由最小热导率 [37] 的 Cahill 和 Pohl 模型近似的热导率为 1.38 W m ⁻¹ K ⁻¹ 对于同一部电影 [47]。据报道，通过溅射沉积的非晶二氧化钛薄膜的热导率为 1.6 W m ^-1 K ⁻¹ 对于 920 纳米厚的薄膜 [38, 51]。纳米管获得的热导率小于这些报告中处理的无定形二氧化钛薄膜的热导率 [38, 47, 51]。然而，相对较低的热导率 0.7 W m ^-1 K ⁻¹ [52] 还报道了通过溅射和 0.9 W m ^-1 制备的 150 nm 厚的非晶二氧化钛薄膜 K ⁻¹ [53] 通过溶胶-凝胶法制备 120 nm 厚的薄膜。在薄膜的情况下，基板、薄膜和金属换能器薄膜之间的热边界电阻被认为将整体热导率降低到非晶极限以下 [52]。在纳米管的情况下，纳米管之间的热接触电阻、表面粗糙度和制备过程中结构中的杂质等因素也会影响净热导率。郭等人。 [34] 提出与结晶纳米管相比，非晶纳米管阵列之间的热接触电阻值更高。 0.85 W m ⁻¹ 的热导率 K ⁻¹ 已经报道了单个非晶纳米管 [32]，而郭等人。 [34] 报道了 0.617 W m ⁻¹ 的热导率 K ⁻¹ 用于沿管方向的非晶纳米管阵列。对于 TNTA,T，热导率为 0.75 W m ⁻¹ K ⁻¹ 获得。该值与通过水热法制备的钛酸盐纳米管 [1, 33] 的公开结果非常吻合。还注意到热导率随着表 1 中所示材料密度的增加而增加。测量的 TNTA 密度 (3.79 g cm ^-3 ) 接近 3.89 g cm ⁻³ 的整体锐钛矿密度 [34]。 TNTA,T 的密度也与测量的混合钛酸盐和二氧化钛纳米结构压块的密度相关 [54]。 TNTAmor 的密度为 3.67 g cm ⁻³ , 接近于报道的非晶二氧化钛薄膜的密度 (3.73 g cm ⁻³ ) 由 ALD [55] 沉积。氧化铝薄膜的热导率与密度的线性相关性在[55]之前已有报道。

声子平均自由程已计算为二氧化钛 [1] 为 2.5 纳米，二氧化钛纳米纤维 [28] 为 1.21-3.15 纳米，二氧化钛纳米管 [32] 为 2-3 纳米。在本报告中研究的三种不同类型的纳米管中，锐钛矿纳米管 (TNTA) 的热导率值最高，而多壁 TNTA,T 的热导率低于 TNTA 和 TNTAmor。图 5 显示了当前和以前公布的热导率值与 TNT 壁厚的比较。通过水热法、[1, 33] 第三代阳极氧化阵列 [34] 和单纳米管 [ [图 32]，并将通过本 RBA 和化学处理方法生产的纳米管的值与其壁厚和热导率的平均值绘制成图（图 5）。图 5 显示结晶二氧化钛纳米管的热导率通过减小壁厚而显着降低。随着壁厚的减小，热导率的抑制归因于壁厚的声子限制[32]。尽管 Brahmi 等人没有观察到这种效果。 [32]，显然由于样本尺寸减少的限制，建议的减少是用目前的 TNTA,T 观察到的。图 5 显示了非晶纳米管的类似趋势，热导率随壁厚降低。通常，无定形纳米材料预计具有类似的热导率，而与尺度无关，因为热传输归因于非传播扩散 [47]。根据材料及其尺寸，传播体（传播振动）也可能对整体热导率做出贡献 [35]。温格特等人。 [35] 提出通过将薄膜厚度从微米范围缩小到纳米范围来降低非晶硅薄膜的热导率。后来，Kwon 等人通过实验证实了非晶硅的尺寸依赖性热导率降低。 [36] 由于传播对整体热传输的贡献。发现非晶硅的载体的平均自由程在 10 nm 到 10 μm 的范围内，它们在室温下使热导率增加了 30% [36]。估计无定形二氧化钛的平均自由程在 0.195-0.201 nm（≈ 原子间距离）[56] 的范围内。没有发现说明二氧化钛中传播体的平均自由程的研究。然而，也观察到非晶 TNT 的热导率随着壁厚的减小而降低（图 5）。因此推测TNTs中的热传输不仅归因于扩散子，而且propagons也可能有助于整体热导率，这降低了非晶纳米管的热导率，并随着壁尺寸的缩小而降低。

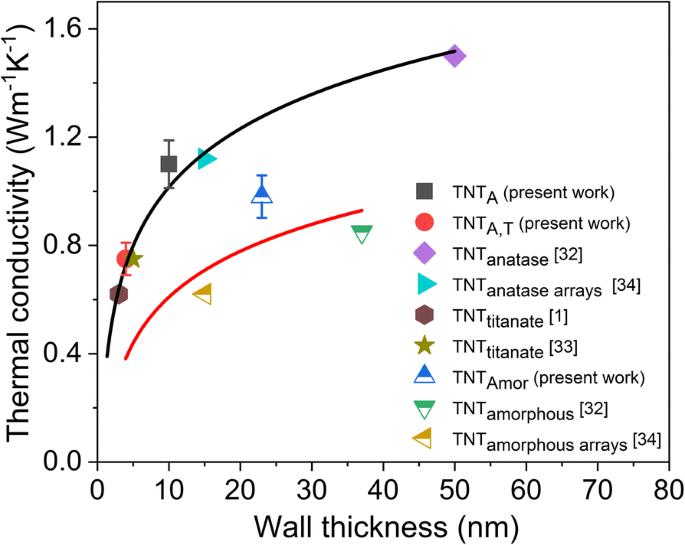
结晶和非晶二氧化钛纳米管的热导率与其壁厚有关。添加趋势线以提供视觉指导

有人提出，纳米管的热性能取决于它们的壁厚而不是直径 [1, 32]。 Gao 和 Jelle 提出了热导率随壁厚降低的理论近似值 [1]，这是对早先提出的模型的修改 [44]。然而，整体热导率也受纳米管表面粗糙度的影响。梁和李 [44] 通过表面粗糙度参数 (p ) 如下：

其中 κ TNT 是纳米材料的热导率，κ B 是体热导率，l o 是声子平均自由程，L 是壁厚，L o 是晶体的几乎所有原子都位于其表面的临界尺寸 [44]。需要注意的是 L o =2(3 − d )w , where d is the dimension of the material (which is 1 in the case of nanotubes) and w is the atomic or molecular diameter [1, 44]. Finally, α is a material constant = 2Sv /3R  +  1, where Sv is the bulk vibrational entropy and R is the ideal gas constant [44]. The phonon mean free path of the titania nanotubes calculated from the kinetic formula of lattice thermal conductivity was reported to be 2.5 nm [1]. The bulk thermal conductivity of titania (κ B) is 8.5 W m ⁻¹  K ⁻¹ as noted previously. The values for w , Sv , and α are obtained from the study by Gao and Jelle [1]. The surface roughness factor p obtains values from 0 to 1, where smaller value of p corresponds to a rougher surface and diffusive phonon scattering and larger values correspond to smooth surfaces with specular phonon scattering [1, 32, 44]. Figure 6a shows the thermal conductivities of crystalline nanotubes for different wall thicknesses and scattering factors. p factor of 0.4 was found best for estimating the thermal conductivity of 2-nm rutile nanoparticles in [57] as well as for silicon nanowires having the diameter of 20–100 nm in [44]. The same p value of 0.4 has also been used for titanate nanotubes by Gao and Jelle [1], who theoretically estimated thermal conductivity values of TNTs between 0.30 and 0.77 W m ⁻¹  K ⁻¹ for 2–3-nm wall thickness. Contrary to the previous reports, by using Eq. 7 our experimental data for TNTA,T fit with the p factor of 0.26 as shown in Fig. 6a. The practical value is plotted at a maximum wall thickness. For TNTA, the thermal conductivity value obtained by using Eq. 7 at the maximum wall thickness (12 nm) fits with the calculated surface roughness factor of 0.18. These small values are associated with the rough surface of the anodized nanotubes. p factor corresponds to p =  1 − 10η /L , where η is the surface roughness of nanotubes and L is the thickness of the material [44]. This equation gives the approximation of surface roughness of 0.22–0.29 nm for TNTA,T and 0.56–0.96 nm for TNTA. These values correlate quite well with the roughness values estimated from the TEM micrographs. The difference in surface roughness for both nanotubes results from the synthesis process. It is pointed out that the thermal conductivity increases with increasing wall thickness for both crystalline nanotubes. This provides experimental verification for the model proposed by Liang and Li [44] and modified for nanotubes by Gao and Jelle [1], where thermal conductivity increases with an increase in wall thickness. The decline in the wall dimensions leads to the reduced phonon mean free path by phonon confinement and increased diffuse phonon boundary scattering, resulting in overall reduction in thermal conductivity values [32]. The crystal defects as well should influence the net thermal conductivity value along with the thermal contact resistance between the nanotubes, which are not considered here. Equation 7 is also adapted for the amorphous nanotubes (TNTAmor) and the maximum value of wall thickness (30 nm) is plotted in Fig. 6b. The bulk thermal conductivity (κ B) of the titania is estimated as 1.6 W m ⁻¹  K ⁻¹ [38] from the minimum thermal conductivity model and l o is estimated as 0.198 nm [56]. The experimental value fits well with the p factor of 0.65 for amorphous nanotubes, which gives the surface roughness of 0.99–1.98 nm for the TNTAmor. The mean roughness of TNTAmor estimated from the TEM images (1.5 nm) fits well with this theoretical range. The surface roughness in one-dimensional crystalline nanostructures (< 100 nm) has a strong impact on the overall thermal conductivity reduction due to the diffusive phonon boundary scattering [58, 59]. In the case of amorphous material, the surface roughness could play a role if it approaches the wavelength of the propagons [36].

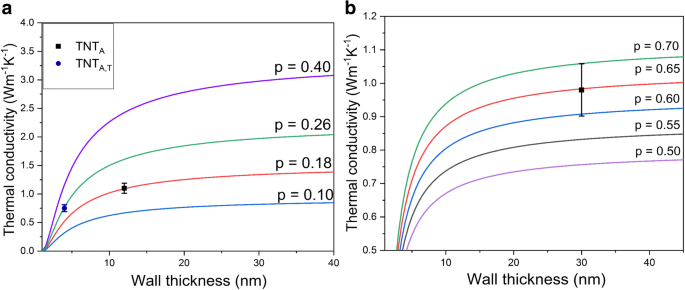
Size-dependent thermal conductivity of a crystalline titania nanotubes (TNTA and TNTA,T) and b amorphous nanotubes (TNTAmor) with different surface roughness factors; symbols show the experimental thermal conductivity of the studied titania nanotubes and the solid lines indicate the calculated thermal conductivities by using Eq. 6

结论

Three different kinds of titania nanotubes are synthesized with different crystal structure and morphology by using chemical processing and rapid breakdown anodization methods. Based on the measurement results at room temperature, the thermal conductivity of the titania nanotubes is considerably lower as compared to the bulk titania. Titania (TNTA) nanotubes are single-walled with one end opened and other closed, and they have anatase structure and a wall thickness of 7–12 nm. The thermal conductivity of these nanotubes estimated by an effective model of thermal conductivity is 1.07 W m ⁻¹  K ⁻¹ . The amorphous nanotubes (TNTAmor) with a wall thickness of 15–30 nm have a thermal conductivity of 0.98 W m ⁻¹  K ⁻¹ . Their thermal conductivity is slightly lower than that of crystalline anatase nanotubes (TNTA). However, the multiwalled and open-ended nanotubes (TNTA,T) with a mixed crystal structure and a wall thickness of 4–5 nm have the lowest thermal conductivity of 0.75 W m ⁻¹  K ⁻¹ . This low value of thermal conductivity is due to the reduced dimensions of walls approaching the calculated 2.5-nm phonon mean free path. The reduction in the wall thickness is found to result in overall suppression of the thermal conductivity as the phonon confinement is enhanced and the phonon boundary scattering increased. The size confinement effects of phonon transport with different surface-related parameters for both crystalline and amorphous nanotubes are considered. Generally, the thermal conductivity of amorphous oxides is found independent of the size. Comparison of the present result on the amorphous nanotubes with those in the literature, however, suggests also size-dependent reduction in the thermal conductivity of the amorphous nanotubes. This may be due to the possible contribution of propagons in the overall thermal transport in disordered structure along with the diffusons. For TNTA,T, the thermal conductivity value agrees well with the surface roughness factor of 0.26, while in the case of TNTA nanotubes, it matches with 0.18 confirming the different surface roughness of the two kinds of crystalline nanotubes related to the synthesis processes. TNTAmor surface roughness (1.5 nm) estimated from TEM micrographs is in line with the calculated surface roughness factor of 0.65.

缩写

RBA:

Rapid breakdown anodization

SEM：

扫描电镜

TEM：

透射电子显微镜

TNTA :

Titania nanotubes with anatase crystal structure

TNTA,T :

Titania nanotubes with mixed crystal structure (anatase and titanate)

TNTAmor :

Titania nanotubes with amorphous structure

TNTs:

Titania nanotubes

XRD：

X射线衍射