固体氧化物燃料电池阳极的各向异性微观结构演变

背景

固体氧化物燃料电池（SOFC）是一种将氢的化学能直接转化为电能的电化学装置。单个电池通常具有平板形式，其中不透水且致密的离子导电电解质夹在两个多孔催化电极之间：阳极和阴极。燃料供给阳极侧，空气供给阴极。气体不能混合以避免非生产性燃烧。相反，气体撞击催化剂材料，失去电子，并在电解质的两侧形成电容器。由于阴极侧的反应较慢，因此两个电极之间会出现电位差。这种电位差与氧气压力梯度一起，是将氧离子从阴极移动到阳极的驱动力。在这方面，电极微结构的形态至关重要。典型的阳极由镍相 (Ni)、氧化钇稳定的氧化锆相 (YSZ) 和孔隙相组成。通过为不同物种提供途径，每种材料在跨 SOFC 的运输过程中都发挥着重要作用。在阳极的情况下，YSZ 相提供了通向氧离子的通路，Ni 相提供了电子，孔隙相允许气体穿透电极。电化学反应只能发生在所有三相接触的线上，即所谓的三相边界 (TPB)。跨细胞的传输现象如图1所示[1]。

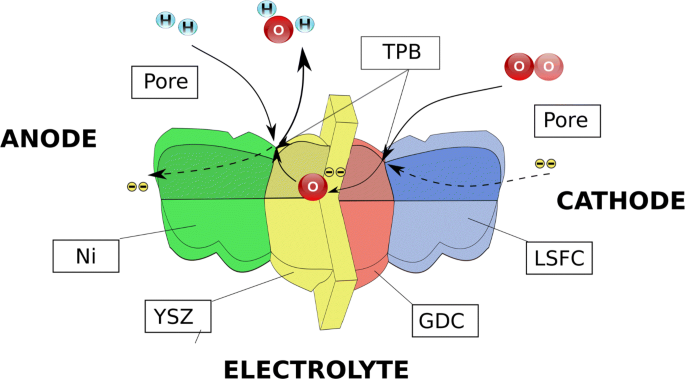
典型的固体氧化物燃料电池的输运现象示意图，突出了微观结构的作用

由于阳极复合材料的复杂性，面向微观结构的设计成为 SOFC 开发的关键步骤 [2-7]。在这项工作中，我们研究了固体氧化物燃料电池阳极在长时间运行中发生的微观结构变化。为了提供深入的分析，我们专注于反映给定方向上微观结构复杂性的各向异性曲折系数。使用与聚焦离子束耦合的扫描电子显微镜进行结构分析。该技术于 2006 年由 Wilson 等人引入 SOFC 领域。 [8]。该方法允许直接观察许多后续部分，并将结果转换为微观结构的 3D 数字表示。从重建的微观结构，可以评估微观结构参数 [9-11]。这些参数直接从真实电极结构中获得，对于了解燃料电池系统长期运行过程中阳极微观结构的演变至关重要。该技术被广泛用于改进数值建模 [12-17]，最近还用于了解固体氧化物燃料电池阳极的降解机制 [18-24]。这成为对最近晶体学研究的宝贵认可 [25, 26]。

在本文中，我们首次报告了 SOFC 堆长期运行过程中微观结构演变的各向异性特征。结果表明，微观结构的演变主要是由于镍颗粒的各向异性迁移、生长和粗化。

实验光圈

模块化堆栈测试平台

老化测试是使用由欧洲领先的 SOFC 制造商 SOLID Power 设计和开发的模块化堆栈测试台 (MSTB) 进行的。装置示意图见图2。电堆位于电炉内。

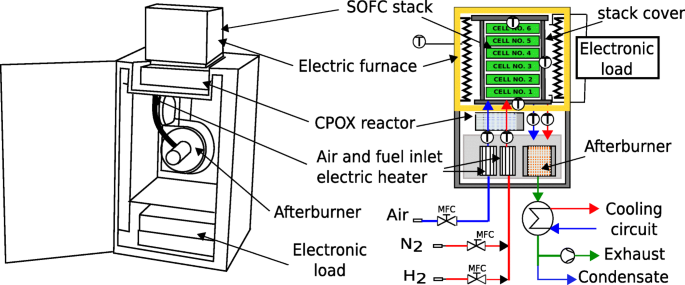
模块化堆栈测试台示意图

燃料和空气通过质量流量控制器和预热器供应给系统。空气和燃料都被送入催化部分氧化 (CPOX) 反应器（如果燃料含有甲烷），或者如果燃料是氢气和氮气的混合物，则绕过它。预热后向阴极通道供应空气。进料空气中的部分氧气在电化学反应中被消耗。同时，空气用于从电池堆中去除热量。然后，空气被输送到加力燃烧室以燃烧来自阳极通道的未使用燃料。在空气处理的另一端，燃料被氧化以发电。本研究中的燃料是氢气 (H2) 和氮气 (N2) 的混合物，预热后被送入阳极通道。残余燃料在加力燃烧室中被氧化。燃烧过程结束后，气体被冷却，冷凝水被分离，干燥的气体最终被排放到环境空气中。

图 2 中标有“T”的七个热电偶监测温度分布。每个双极板都连接到电线，然后连接到恒电位仪。这种配置允许获得电池组中每个电池的电流-电压特性。电池的尺寸为 60 × 80 [mm × mm]。可用于反应的活性细胞面积为 48 [cm ² ]。该电池燃料利用率高达75%，可实现大于1 [W cm ⁻² 的高功率密度 ]。烟囱采用共流配置，燃料和空气流方向相同。系统采用氢气和氮气混合燃料作为燃料。

有关设置的更多详细信息，请参见其他地方 [27, 28]。

聚焦离子束-扫描电子显微镜

双光束系统在一个腔室中结合了扫描电子显微镜 (SEM) 和聚焦镓离子束 (FIB) 源。 SEM 用于成像，FIB 主要用于铣削。对于有限的情况，可以使用 FIB 进行观察。该系统为研究样本的后续部分提供了独特的可能性。可放置在支架中的材料样品通常尺寸为 25 mm ² . FIB-SEM 设置和测量程序如图 3 所示。离子枪方向垂直于样品表面，电子枪相对于离子源倾斜一定角度，以允许对样品截面的观察。在单个程序中可以观察到的样品的感兴趣体积约为 1000 μ m ³ .聚焦离子束用于制造沟槽并暴露满足最小代表性体积尺寸要求的样品交叉点。沟槽制作完成后，交点用低能Ga ⁺ 抛光 光束和图像是使用镜头内检测器拍摄的。这在所研究的相之间产生了非常好的对比：Ni、YSZ 和孔隙。拍摄 SEM 图像后，FIB 枪铣削以暴露另一个交叉点，并去除另一层材料。根据感兴趣的体积，重复“cut-and-see”过程直到获得 200-300 个图像。此过程称为切片。该过程可以概括为以下步骤：

1. 1

   碳层沉积在感兴趣的体积上。

   <图片>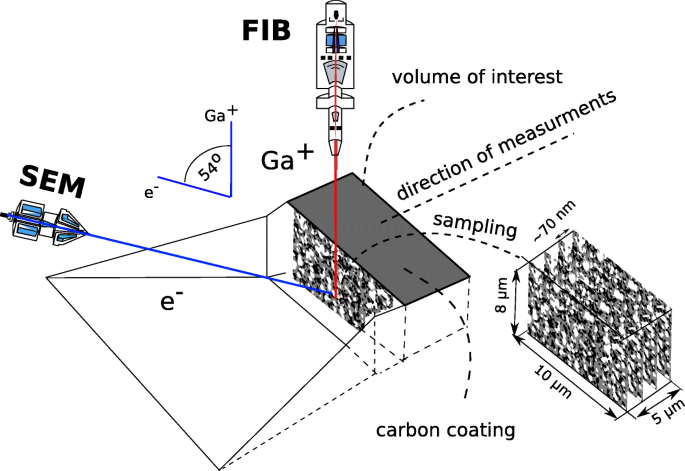

   双光束系统的配置

2. 2

   制造一个沟槽以进入样品的交叉点。

3. 3

   断面采用小电流束抛光。

4. 4

   使用透镜内二次电子检测器拍摄观察到的交叉点的SEM照片。

5. 5

   FIB 枪使用 Ga+ 离子束研磨样品以暴露另一个交叉点。

6. 6

   重复“剪切并查看”过程以获得二维图像序列。

剪切和观察程序的思想如图3所示。

实验方法

所提出的研究分为两个独立的部分：发电实验和微观结构研究。耐久性研究是通过在长时间内将堆栈保持在恒定负载下进行的。为了减少测试的持续时间，温度升高到 800 ^o C 和施加的电流为 19.4 A，以在实验开始时提供 90 W 的输出功率。燃料利用率为75%。详细的实验条件总结在表1中。老化测试后，将电堆拆开，选择9个样品进行测试后的微观结构分析。从细胞中提取了三个样品。 1、3 和 5（位于每个单元的上游、中心和下游），如图 4 所示。另外一个单元，即所谓的参考单元，是还原过程之后的一个新单元。电池由制造商提供，不参与电化学测试。因此，可以合理地假设参考电池的微观结构代表老化试验之前的微观结构。用于 FIB-SEM 分析的所有样品均为 5 mm × 5 mm 正方形，并使用金刚石笔从单元（6 cm × 8 cm）上切下。在进行微观结构研究之前，所有样品都用环氧树脂浸渍并用砂纸抛光。浸渍对于在 SEM 成像过程中识别孔隙相很重要。 9个样品均采用FIB-SEM技术进行分析。

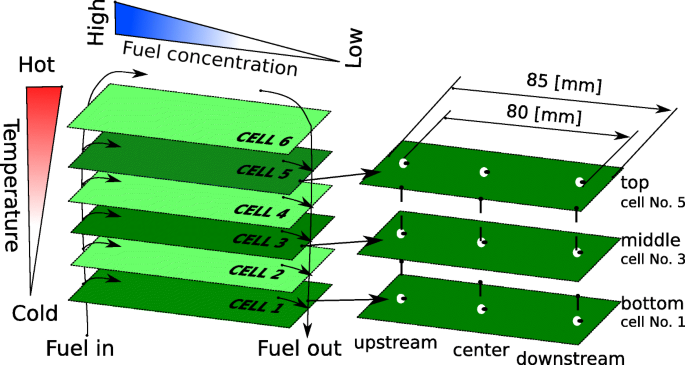
所选样本在单元格和堆栈中的位置

为每个样品获得的一组 SEM 图像经历了图像分割过程，以将三个阶段中的一个分配给 SEM 图像的每个区域。分割是根据图像区域的亮度标记图像区域的过程，该过程半自动进行，每个样本需要操作员长达一个月的工作时间。图像分割过程成功后，进行图像重采样（见图5）。

图像处理和相位标记的工作流程。 一 原始图像。 b 手动移除实验工件。 c 过滤。 d 相标记，白色代表镍，黑色代表气孔，灰色代表YSZ

本文稍后介绍的随机游走模拟需要立方体素。这意味着图像之间的距离应该等于图像的像素大小。然而，更多的切片表明分割需要更多的时间，这实际上是不可行的。在实践中，图像之间的距离比像素大小更重要，以在最耗时的分割过程中节省时间。因此，对立方体素进行分割，并在后处理期间转换为立方体素。基于重新采样的图像，代表每个相的三维形态的表面是通过不同区域之间界面的三角形近似生成的。三角测量和重采样是使用 ThermoFisher Scientific 的 AVIZO 软件进行的。获得的三维数字材料表示如图6所示。

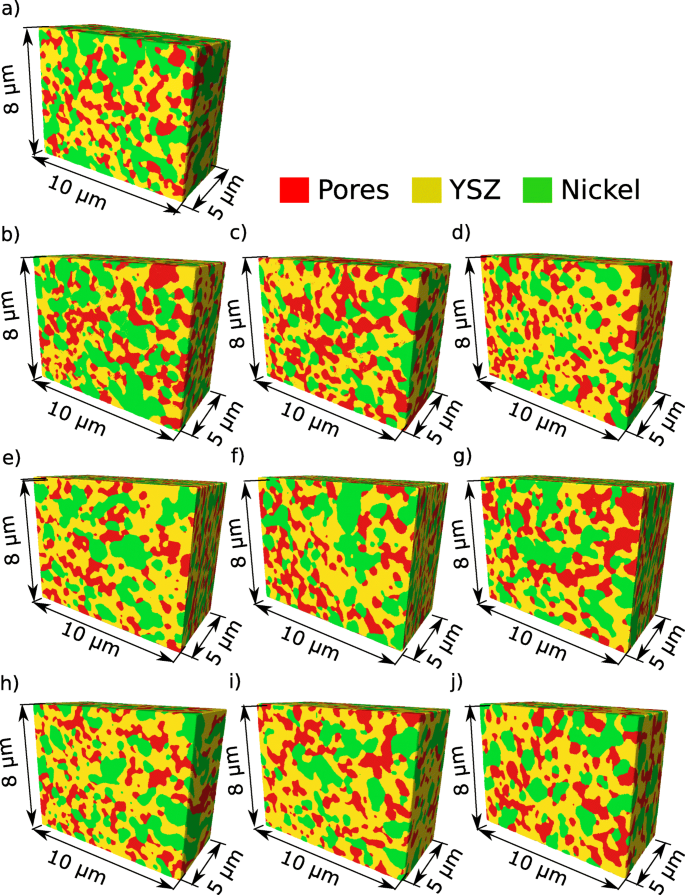
老化试验前后阳极微观结构的数字材料表示。 一 参考样品。 b 单元 5 上游。 c 单元 5 中心 d .下游单元 5 e 单元 3 上游。 f 单元格 3 中心 g .细胞 3 下游。 h 小区 1 上游。 我 单元格 1 中心。 j 细胞 1 下游

曲折系数是微观结构复杂性的定量度量。 Carman [29] 将曲折的概念引入到多孔介质研究中，他研究了通过沙床的流动。他引入了曲率作为考虑多孔介质内流体的细​​长扩散路径的因素。在他的研究中，他假设厚度为 L 的多孔床 s 可以看作是一束具有均匀横截面和长度L的弯曲毛细管 e .类似地，对于固体氧化物燃料电池阳极，曲折度可以定义为实际扩散路径长度与电极厚度的比值。在这个简化的系统中，曲折度定义为实际扩散路径长度的比值，L e , 到直通道情况下的路径，L s （阳极厚度）：

记住曲折度和曲折系数之间的区别很重要。根据 Carman 的公式，曲折因子 (τ ) 定义为曲率的平方 (τ =\(\bar {\tau }^{2}\))，在质量扩散方程中用作增强因子：

其中 ε 是孔隙率，D 我 是气体香料i的扩散系数 在混合气体中，D 我 ,eff 为考虑多孔介质内流体的细​​长扩散路径的有效扩散系数。

在真正阳极的微观结构中，燃料路径可能非常复杂，气体连接路径可能会产生许多分支、分离和重新连接。因此，将曲折系数表示为曲折的平方具有一定的象征意义，曲折与曲折系数之间的真实关系无法使用毛细管模型计算。一些小组使用所谓的 M 因子来克服这个问题，该因子明确地将几何曲折、渗透因子 (P ), 收缩因子 (β ), 相体积分数 [30]:

其中 a , b , 和 c 是源自参考文献中描述的方法的常数。 [31]。 Peterson [32] 引入的constriction factor 可以理解为bugles 和bottlenecks 之间的比率。可以在 Tjaden、Brett 和 Shearing [33] 的评论中找到对现有方法来估计曲折系数的全面回顾。

最近，基于扩散的算法受到越来越多的关注，因为它们不需要限制因素。这是因为在模拟扩散过程时直接考虑了瓶颈和凸起，实测值是扩散系数的直接折减[34]。

这里最有前途的方法之一是随机游走过程，它可以统计计算非吸附粒子的曲折系数。在该方法中，大量称为随机游走的标记随机分布在孔隙相中，如图 6 中的红色体积所示。在每个时间步长，每个游走随机迁移到同一相的相邻体素。如果为迁移选择的体素属于不同的阶段，则步行者停留在当前位置并等待下一个时间步。重复这个过程，可以计算出随机游走者的均方位移：

哪里𝜗 是随机游走过程的无量纲时间，n 是随机游走者的数量。

自由空间中晶格游走的均方位移的精确解由[35]给出：

其中 D 0 是自由空间中的扩散系数 [m ² s ⁻¹ ] 和 t 是 [s] 中的时间。来自方程的扩散系数。 (5) 可以通过计算导数重写为时间的函数：

因为𝜗 是时间的函数 t , 方程(6)采用如下形式：

部分 \(\frac {\mbox{{d}} \vartheta }{\mbox{{d}}t}\) 可以从方程的一部分导出。 (5):

给予

其中 a 是简单立方晶格的晶格常数（即 FIB-SEM 体素的尺寸）[nm]。

曲折系数τ 描述了与自由空间相比，多孔介质中均方位移的减少程度 [34, 36]：

通过结合方程。 (7) 和 (10) 得出以下公式：

在进一步合并方程之后。 (8)和(10)变成：

当只考虑一个方向的传输现象时，以下表达式是相关的：

因此，对于各向异性曲折系数的估计，方程。 (12)变成：

由于该方法基于统计量，因此需要许多步行者和大的均方位移才能正确估计曲折因子。最终，步行者将离开由微观结构的数字表示所代表的计算域。这当然是不可取的，因为步行不能继续超出计算域。相位镜像用于避免这个问题。当步行者越过边界时，它完全出现在一个新的域中，这个域是原始微观结构重构的镜像。每当步行者越过边界时制作数字重建的完整副本对于计算机内存来说太重了，因此，应用了特殊的编程技术来节省硬件资源。相位镜像是该方法的主要限制，因为计算出的曲率仅反映了所研究的感兴趣体积（而不是整个阳极）的复杂性。

基于各向异性曲折度，我们引入定义如下的各向异性因子：

其中 τ x ,τ 是 , 和 τ z 是 x 中的各向异性曲折因子 , y , 和 z 方向，分别为 τ r 是为步行者总位移计算的曲折系数，与位移发生的方向无关。

结果与讨论

图 7 显示了老化测试期间电池组的平均端电压。可以看出，没有性能降低的证据。此外，在前一千小时的运行中，极化会减少。我们之前的结果表明，尽管没有性能恶化，但反应表面接触面显着减少 [24]。我们发现 TPB 的衰减是非均匀的，并且强烈依赖于堆栈中的位置 [24]。在本文中，我们表明微观结构的演变不仅是不均匀的，而且是各向异性的。阳极的复杂性是根据使用图 6 所示的数字材料表示导出的各向异性曲折系数估算的。

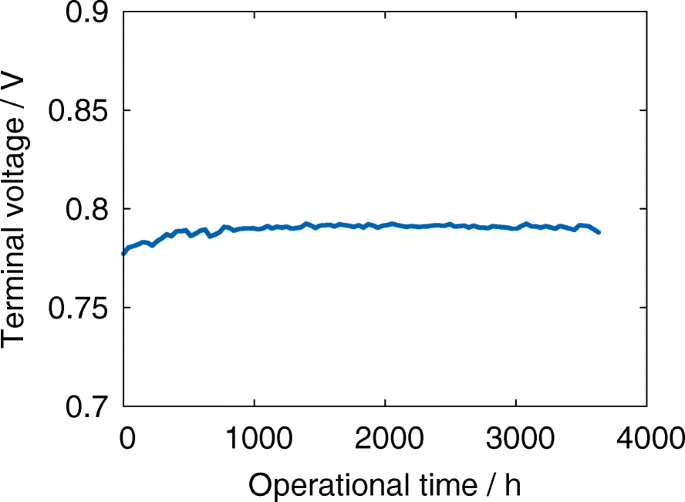
长期运行期间作为运行时间函数的端电压

备注 在实际实验中，由于实验工件的存在，所获得的感兴趣体积的直径各不相同。最常见的伪影，例如窗帘效果、阴影和再沉积，可能会限制可访问的横截面。因此，每次测量可以适当识别和分割的体积是不同的。在某些情况下，我们可以获得超过 10 μ z 中的 m 方向;然而，由于窗帘影响音质，y中的图像 方向有限。对于其他人，图像在 y 中很清晰 方向，但我们只能正确对齐有限数量的图像。对于定量，每个体积约为 1000 μ m ³ .然而，仅仅为了可视化，我们将图像修剪到一个常见的尺寸 10 μ m × 8 μ m × 5 μ m 以便在图 6 中并列和比较它们。

曲折因子估计的方法在“实验方法论”部分进行了简要介绍。图 8 显示了电池和堆栈中不同位置的各向异性因子。还提供了与参考样品的比较。结果中观察到的一个共同趋势使我们得出以下结论：

• 参比负极材料具有各向同性，在老化试验过程中演变为强各向异性。

  <图片>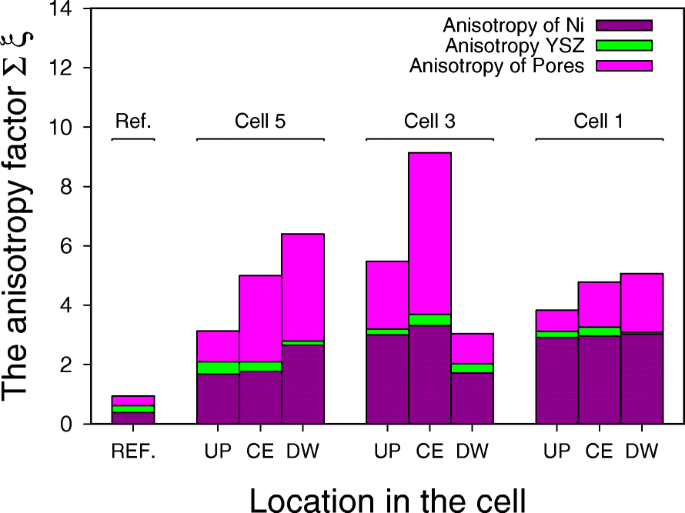

  电池堆内不同位置的各向异性因子，其中UP、CE、DW分别表示电池的上游、中心和下游，缩写REF对应参考电池

• 总的趋势是各向异性因子随着细胞向下游移动而增加。

• 仅对镍相和孔相观察到强各向异性。钇稳定的锆保持各向同性。

各向异性的可能原因是在我们之前的研究 [23, 24, 40] 以及其他研究小组 [18, 41] 中观察到的镍颗粒粗化 [37-39] 和迁移。在长期运行过程中，镍颗粒从阳极电解质界面向阳极表面迁移。由于迁移主要发生在一个方向，因此导致微观结构的各向异性。这也可以解释为什么各向异性只影响镍相和孔隙相。详细机制尚不清楚，但镍颗粒从阳极-电解质界面向阳极表面迁移的可能原因是挥发性镍物质（如氢氧化镍）的蒸发沉积。这会导致镍的电子传导路径不均匀和不连续[42]。

今天在 SOFC 模拟中使用的大多数气体扩散模型都假设一个均质多孔电极。对于大多数应用来说它是准确的，但我们的结果表明这种同构假设在退化后可能不成立。本文中观察的直接含义是，当人们希望将老化样品的微观结构参数应用到数值模拟中时，重要的是要记住模型中考虑的传输现象的方向。因此，应从微观结构参数中提取适当的各向异性属性（如果检测到各向异性）。基于所获得的结果，可以得出结论，当考虑扩散时，各向异性尤其重要，因为曲折因子定量地表达了扩散系数的减小率。将长期运行后获得的不同阳极的微观结构参数并列时注意各向异性方向是本次观察的另一个实用建议。

一般结论

在本文中，我们首次证明了 SOFC 的长期运行会导致阳极微观结构的各向异性。使用短堆栈进行扩展发电实验。在老化测试之前和之后使用 FIB-SEM 纳米断层扫描进行局部分辨的微观结构分析。将获得的阳极微观结构的 3D 重建实施到基于扩散的算法中，以计算各向异性曲折系数。结果表明，长期运行导致所研究阳极的镍相和孔隙相具有很强的各向异性。老化试验后阳极各向异性性能的可能原因是镍颗粒的迁移、生长和粗化。

数据和材料的可用性

由于数据构成正在进行的研究的一部分，因此目前无法共享重现这些发现所需的原始数据和过程数据。

缩写

CPOX：

催化部分氧化

FIB：

聚焦离子束

MSTB：

模块化堆栈测试台

SEM：

扫描电子显微镜

SOFC：

固体氧化物燃料电池

TPB：

三重相界

YSZ：

氧化钇稳定氧化锆