检测自组织 InAs/InGaAs 量子点超晶格中的空间局域激子：提高光伏效率的一种方法

背景

由于三维载流子限制的性质和类似 δ 的态密度，自组装量子点 (QD) 已被广泛研究用于光电子学的可能应用。最近，提出了 QD 结构来实现中间带太阳能电池 (IBSC)，它通过价态 IB 和 IB 导带吸收引入额外的光载流子 [1]。具有比 GaAs 能隙更小的量子点的 GaAs 基 IBSC 形成串联结构，该结构能够吸收能量低于 GaAs 能隙的光子，从而导致更高的能量转换效率 [2]。量子点中间带的形成需要高密度量子点的密堆积多层结构 [3, 4]。然而，由于内部压缩应变的积累，InAs QD 的晶体质量随着 QD 层数的增加和层间距的减小而降低。过大的应变会导致位错和缺陷，这些位错和缺陷从 QD 向上延伸到表面。因此，InAs/GaAs QD SC 的性能也会随着 QD 层数的增加而降低 [5]。为了克服这些问题，已经使用用于 InAs/GaAs 材料系统的 GaAsN、GaAsP 和 GaP 缓冲层证明了应变补偿生长技术 [6,7,8]。克服这些问题的另一种技术是用薄的 InGaAs 应变降低层覆盖 InAs/GaAs QDs 层。与 InAs/GaAs QD 相比，由于 InAs 和 InGaAs 之间存在小的晶格失配，该层会导致光响应发生红移。温度相关的光致发光研究提供了关于多层 InAs/GaAs QDs SC 的有用信息，具有相当大的实践和理论意义。传统上，半导体材料的带隙随着温度的升高而单调减小。由于量子点集合内的热激活载流子转移机制，特殊材料（例如 InAs/GaAs QD）在低温下显示出 PL 异常。然而，如 Ilahi 等人所示，这些异常在 InAs/InGaAs/GaAs QD 异质结构中的生长后混合过程后逐渐消失。 [9]。 Sayari 等人研究了与本研究相似的异质结构在光伏应用中的效率。 [10]。在过去的几十年中已经提出了许多模型，例如 Passler、Vina 和 Varshni 模型。为了生产可靠的器件，必须充分了解此类 InAs/InGaAs/GaAs QD 异质结构的温度特性，这是通过使用最佳拟合模型。我们在此使用修正了热再分布系数的 Passler 经典模型，以便更好地理解所观察到的激子带隙的 S 形温度依赖性。我们的研究为 InAs/InGaAs/GaAs QD 异质结构中的载流子定位和转移提供了自洽的精确图片，这是一种用于制造高效光伏器件的技术上非常重要的能源材料。

实验详情

图 1 说明了我们研究中研究的 InAs/InGaAs/GaAs QD 异质结构的示意图。异质结构由五叠 InAs/In0.11Ga0.89As/GaAs QD 层和夹在 80 nm 本征 GaAs 层之间的叠层组成。外延层在 epiready n ⁺ 上生长 -GaAs (100) 衬底使用固体源分子束外延 (SS-MBE) 和 Riber MBE 32P 系统。氧化物解吸后，250 nm n ⁺ 掺杂浓度为 2 × 10 ¹⁸ 的掺杂 GaAs 缓冲液 厘米 ⁻³ 在 520 °C 下生长，然后是 1000 nm n 掺杂的 GaAs 基层，掺杂密度为 10 ¹⁷ 厘米 ⁻³ .然后将衬底温度降低并稳定在 500°C 以沉积本征区域。如图 1 所示，重复层由 2.5 个单层 (ML) 的 InAs 覆盖层、5 纳米厚的 In0.11Ga0.89As 和 33 纳米厚的 GaAs 组成。通过监测高能电子 (RHEED) 的衍射图，原位控制 QD 的形成。 5 nm 厚的 In0.11Ga0.89As 的目的是使发射和吸收光谱红移，而 33 nm 厚的 GaAs 用作间隔层。 InAs、In0.11Ga0.89As 和 GaAs 层的生长速率分别为 0.08 ML/s、0.78 ML/s 和 0.7 ML/s，通过 RHEED 镜面光斑振荡测量。最后，一个 500 nm p 掺杂的 GaAs 发射极层（2 × 10 ¹⁷ 厘米 ⁻³ ) 后接 100-nm GaAs p ⁺ -掺杂接触层（5 × 10 ¹⁸ 厘米 ⁻³ ) 生长在异质结构的顶部。硅 (Si) 和铍 (Be) 分别用作 n 型和 p 型掺杂剂。生长过程中采用高温计校准温度。

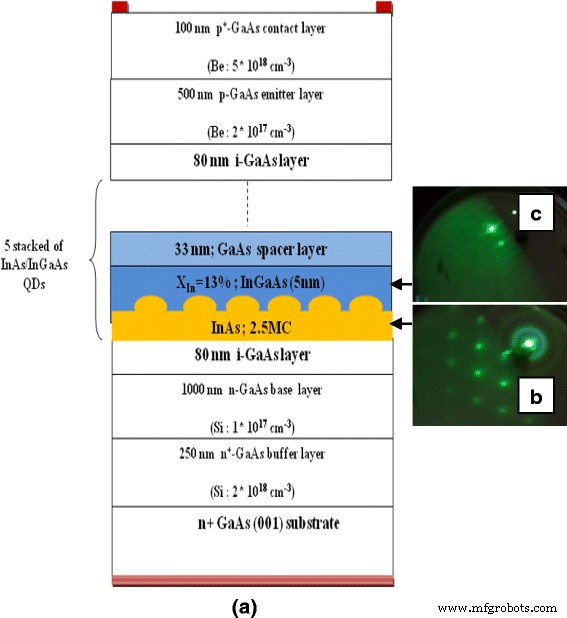
一 在 (001) n ⁺ 上生长的五层堆叠 InAs/InGaAs QDs SC 的层结构示意图 -GaAs 衬底。 b RHEED 在 2.5 毫升 InAs 生长后形成图案（三维生长）。 c RHEED 在 5 纳米 InGaAs 生长期间形成图案（二维生长）[10]

使用 J.A. Woollam 可变角光谱椭偏仪 (VASE) M-2000。 SE 测量是在 45° 到 60° 的入射角范围内进行的。在 PL 测量中，氩离子 (Ar ⁺ ) 波长为 514.5 nm 的激光被用作激发源以产生电子-空穴对。来自样品的发光由高分辨率光谱仪分散，并由带有内置放大器的热电冷却 Ge 光电探测器检测。对于激发功率相关和温度相关的 PL 测量，将样品安装在封闭循环、温度控制的氦低温恒温器中。 PL 光谱是在 1.5–350 mW 的标称输出功率范围和 11–300 K 的温度范围内获取的。时间分辨 PL 测量是在可变温度 (10–240 K)、闭环氦气中进行的低温恒温器。 514 nm 线用作激发波长，来自锁模钛：蓝宝石皮秒脉冲激光器，重复率为 80 MHz，脉冲宽度为 1.2 ps。

结果和讨论

图 2 显示了 InAs/InGaAs/GaAs QD 异质结构在 300 K、能量范围为 1-6 eV 时测量的实部 (a) 和虚部 (b) 介电函数。实部和虚部遵循不同的模式。介电函数随光子能量的变化表明薄膜中光子和电子之间的一些相互作用是在 1-6 eV 的能量范围内产生的。两个主要的光谱特征是分别为 ~3 和 ~4.5 eV 的 E1 和 E2 临界点 (CP) 结构 [11, 12]。为了定量确定不同带间跃迁的能量位置，我们对伪介电函数的虚部的二阶导数谱进行了零交叉。得到的不同跃迁能量总结在表1中。

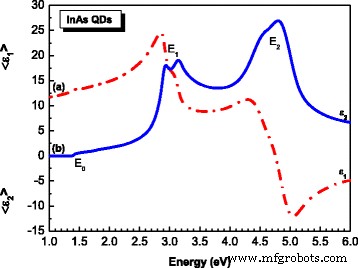
实数 (ϵ 1) (红色虚线 ) 和虚数 (ϵ 2) (蓝色实线 ) 从 SE 测量中获得的 InAs/InGaAs QD 异质结构的部分介电函数 [10]

图 3 显示了图 2 所示伪介电函数的虚部的二阶能量导数谱。2.9 和 3.1 eV 处的两个峰值分别对应于 E 1 和 E 1 + Δ1，GaAs 中的带间跃迁。然而，大约 4.4 和 4.7 eV 处的两个靠近的峰值是由 CP 跃迁 E 引起的 0' 和 E 2，分别在 InAs QD 层中 [12]。我们注意到 E 的贡献 InAs 到 E 的 1 + Δ1 CP 能量 (2.74 eV) [12] 1 一 (2.91 eV) [11] GaAs 不能排除，因为两个能量值之间的差异很小。在低能量下，GaAs 的带隙在 ε 中清晰可辨 大约 1.4 eV 的光谱。此外，二阶能量导数谱（图 3）显示了 1.75 eV 处的带间跃迁，对应于 E GaAs 的 0 + Δ0 CP 能量 [11]。已知ε 2是材料质量的量具和量度；最高值意味着最突然的界面[13]。据文献记载，ε 2 个大约 25 的值，在我们的例子中最高值为 26.8，在 E 区域获得 2 带隙接近 4.7 eV，表明形成由 SS-MBE 生长的 InAs/InGaAs/GaAs QD 异质结构的材料质量高。

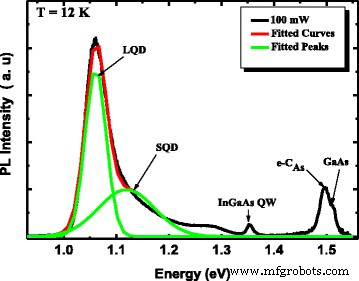
虚部的二阶导数谱 (ϵ 2) 介电函数作为 InAs/InGaAs QD 异质结构的光子能量的函数。 InAs QD 层和 GaAs 层产生的跃迁能量如图所示 [10]

图 4 显示了在低温 (12 K) 下激发功率为 100 mW 的 InAs/InGaAs/GaAs QD 异质结构中有源区的 PL 光谱。显然，光谱呈现出位于高能侧的不对称形状，可以通过高斯拟合在两个子带中进行去卷积[14]。考虑到量子限制势对点尺寸的依赖性，位于 1.06 eV 的最强峰值归因于较大 QD (LQD) 基态的发射，而 1.11 eV 处的较高能量峰值是指来自较小量子点 (SQD) 的基态 [15]。因此，在非常低的激发功率和低温下，我们推断出不对称形状是由于源自点的双峰尺寸分布的发光 [16]。此外，在 1.35、1.49 和 1.51 eV 附近看到源自 InGaAs 量子阱层的峰、GaAs 导带中的电子与碳受体水平 (e-CAs) [17] 上的空穴之间的复合以及 GaAs 带隙，分别。为了确认这种不对称形状的归因，我们在 10 到 100 mW 的不同激光功率下进行了 PL 测量。我们还对类似于所研究的结构的无帽结构进行了 AFM 测量。从图 5 中可以清楚地看出异质结构具有与功率无关的 PL 形状。除了最高激发光谱外，异质结构高能 PL 峰的 PL 强度和线宽没有显着变化。此外，两个 PL 峰之间的能量分离（图 5）约为 50 meV。正如预期的那样，AFM 图像表明第五层中的量子点具有双峰尺寸分布，整个量子点密度为 7 × 10 ¹⁰ cm^(-2)。假设异质结构的低能量侧峰对应于大量子点 (LQD) 的基态，我们可以说高功率下的高能量峰似乎是相对较小量子点 (SQD) 基态的结果).

在低温 (12 K) 下从五层堆叠 InAs/InGaAs QD 异质结构测量的 PL 光谱。光谱的线形分析证明QD PL信号是两个高斯形峰的卷积，如实线所示

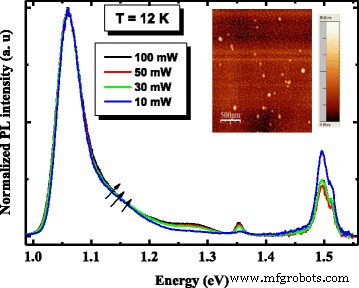
InAs/InGaAs QD 异质结构的激发功率相关归一化 PL 光谱在 12 K 下测量

为了深入了解 PL 重组机制，对 10 到 300 K 的异质结构进行了温度相关的 PL 测量，如图 6 所示。图 7 显示了与 LQD 发射相关的主峰的 PL 能量位置。与传统的 GaAlAs [18] 等其他 III-V 三元合金相比，该峰显示出 10 到 100 K 之间的异常温度依赖性。在此温度范围内（区域 (i)），观察到大约 12 meV 的红移。这种转变是由于激子通过不均匀分布的 LQD 集合内的局域态重组所致。随着温度在该温度范围内升高，载流子被热激活并从集合内的较小 QD 转移到较大 QD，在那里它们最终以辐射方式重新组合。这使得观察到的现象可能源于我们结构中的大点尺寸分散（参见 AFM 插图）。两个复合过程（定域和离域载流子）平等参与PL信号的特征温度表示为T loc/deloc。然后，在 100 到 120 K（区域 (ii)）之间，峰值能量增加。这是由于载流子从较浅的状态逃逸到较高的状态。特征温度表示为 T 逃脱。即使在高温下（区域（iii）），激子完全离域并恢复带间复合。

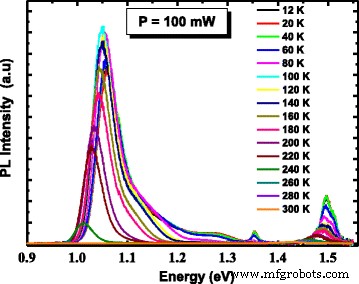
InAs/InGaAs QD 异质结构的温度相关 PL 光谱在 100 mW 的激发功率下测量

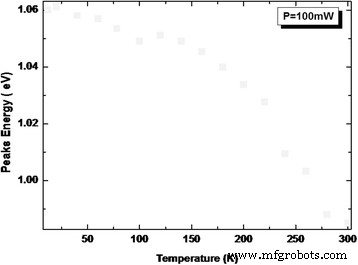
不同温度下所研究的 InAs/InGaAs QD 异质结构的 LQD PL 峰值能量

为了进一步了解 InAs/InGaAs/GaAs 多层叠 QD 中的复合过程，我们使用光计数时间相关技术研究了时间分辨 PL。从理论上预测 QD 的激子衰变寿命对温度敏感 [19]。实验测量表明，寿命确实是低于临界温度的温度常数 [20]。马库斯等人。 [21] 报告了在实验误差范围内在很宽的温度范围内约 950 ps 的恒定寿命。

图 8a 显示了 PL 衰减光谱，在 17 到 240 K 之间，检测能量固定为 1.06 eV，激发能量 (λ exc =514 nm）。这些光谱在理论上通过单指数函数很好地拟合，在较低温度下衰减时间约为 1000 ps。与 III-V 族半导体薄膜 [22] 相比，这种缓慢的衰减时间是存在局域态 [23] 的标志，并且载流子在 LQD 峰的复合应该是纯粹的辐射复合。事实上，在低温下，光生电子和空穴在复合之前需要时间来形成激子并松弛它们的能量以被浅局域态捕获。这些现象导致衰减时间缓慢。已经研究了温度对 PL 衰减时间的影响，并显示了两种不同状态的存在，如图 8b [24] 所示。我们注意到与 PL 带的较低能量 (LQDs (1.06 eV)) 相关的衰减时间在 140 K 之前几乎是恒定的 (1000 ps)，然后随着温度的升高而减少。

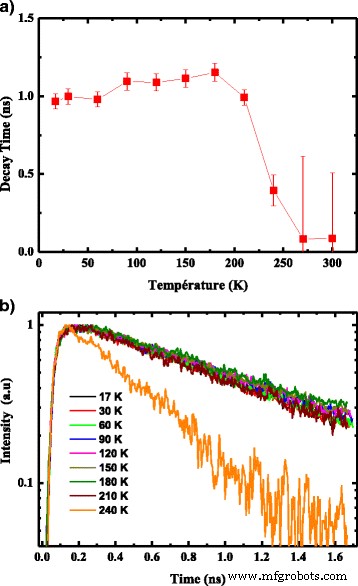
一 对于 514 nm 的波长激发，LQD 峰的衰减时间与样品温度的关系。 b 典型的光致发光衰减强度与在 514 nm 激发波长下测量的 LQD 峰温度的关系

理论方法

为了理解 PL 的异常温度依赖性，使用 Li 等人开发的 LSE 模型研究了 PL 峰值位置。 [25, 26]。事实上，该定量模型为先前在几种 III-V 族材料中观察到的局域态发光的异常光谱特征提供了令人满意的解释，例如硼基 B(In)GaAs/GaAs [27, 28] 合金和 InGaAs/GaAs MQW [29, 30]。该模型假设局域态对于状态密度具有高斯型能量分布：

其中 σ 和 E ch 是局部态分布的展宽参数（局部化深度）和载流子转移必须克服的势垒水平，分别。在准稳态下，局域激子的动力学可以用以下速率方程来描述：

参数τ r , τ tr, γ c, K B、Λ 和 N ' 分别表示载流子复合时间（辐射寿命）、载流子转移时间（非辐射寿命）、重新捕获系数、玻尔兹曼常数、局域态总数和远离热激活的载流子总数本地化状态。 G (E ) 表示载波生成率。数量 \( \frac{\gamma_c N\hbox{'}\left( E, T\right)\rho (E)}{\Lambda} \) 是每单位局部状态重新捕获的载流子数时间。右边的第三项给出了局部载流子的热逃逸率。最后一个代表由于辐射复合导致的载流子减少率。定域载流子的载流子密度与定域载流子的分布函数和态密度成正比。事实上，方程的解。 (2) 可以用方程来描述。 (3).

其中 E 0 是中心能量。在数学上，由 \( \frac{\partial N\left( E, T\right)}{\partial t}=0 \) 确定的局部状态内载流子热重新分布引起的峰值位置的温度依赖性由下式给出:

其中 x (T ) 是非线性方程的数值解。 (5):

方程 5 对于 \( 0 $$ E(T)\approx {E}_0-\frac{\sigma^2}{K_B T} $$ (6)

众所周知，理想化半导体材料的带隙通常由 Passler 经验公式 [32] 描述。考虑到由于热再分布系数引起的校正，使用方程描述的 LSE 模型的发光峰值位置的变化。 (7):

其中 θ 是预期与德拜温度 θ 相当的特征温度参数 D. 对于 T>>θ ，我们看到 α 仅表示一阶导数的大小限制 \( {\frac{dEg(T)}{dT}}_{T\to \infty } \)。指数“p”与底层电子-声子谱函数的形状有关 [33]。该模型与图 9 所证实的实验演化有很好的拟合。拟合参数总结在表 2 中。

LQD 峰的温度依赖性光致发光演变（黑色实心方块 ) 使用经验 Passler 定律拟合（蓝色实线 ) 和 LSE 模型的修正 Passler 关系真值（红色实线 )

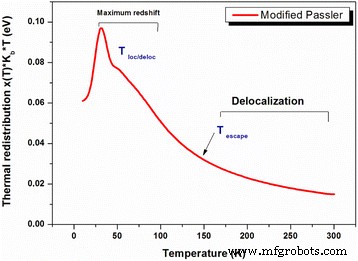
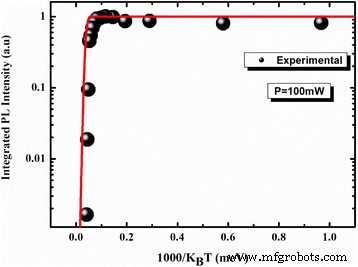
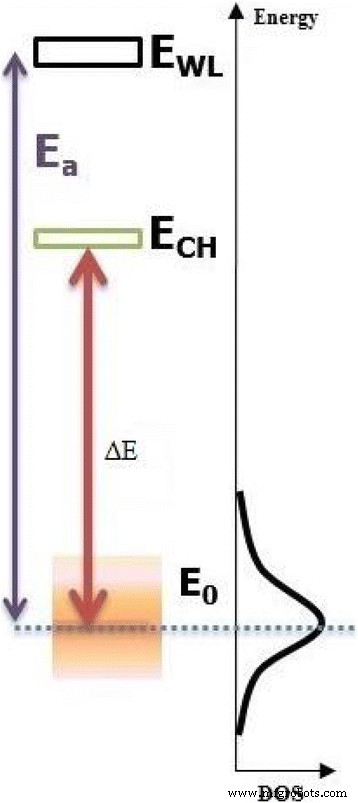
PL 峰值能量很大程度上取决于图 10 中表示的热再分布。这最后表明低温范围内的快速增加。热再分布的最大值对应于能量演化中红移的最大值 (~50–100 K)。在高 PL 温度区域，热再分布呈指数下降并趋于抵消，因为从 150 K 开始离域过程并返回带间跃迁。此外，当经典曲线和修正曲线叠加时，我们可以观察到这一点（图 9）。指数“p”表明纵向声学 (LA) 声子的贡献比纵向光学 (LO ) 声子。这种贡献似乎在高 PL 温度区域占主导地位，其中通过声子辅助发射。双峰分布过程打开了 QD 之间的耦合通道，由能量 E 分隔的离域电子和空穴状态表示 通道这种耦合通道的起源仍然是一个有争议的话题 [34,35,36]。然而，耦合通道可以被视为存在于二维 WL 和零维 QD 状态之间的中间状态 [37]。因此，可以想象，由于所需的活化能较小，QD 状态的载流子比 WL 更容易被热激发到耦合通道，然后转移到有限距离内的相邻 QD。它看起来像费米-狄拉克分布中的费米-狄拉克能级。这种能量E ch 小于活化能 E a 从 Arrhenius 图（图 11）中提取。 E 的原因 a 较大可以解释为载流子需要更大的能量才能到达润湿层 (WL)，如图 12 所示。此外，差值 ΔE =E ch − E 0 在确定局部载流子发光的异常温度依赖性方面起着更重要的作用。我们应该注意到这两种情况，E ch − E 0> 0 和 E ch − E 0 <0，从物理角度来看是存在的，但通常被指定为“正”热活化能。在我们的例子中，这意味着 E ch 比 E 低 4 meV 0 其中局部载流子被热激活到具有更高能量的状态（或真实空间中的位置）。与具有 In0.15Ga0.85As 应变降低底层的单个 InAs QD 层相比，它降低了 [10]。 σ指定的潜在波动深度 是量子点尺寸分布不均匀的结果。发现潜在深度为 19 meV。它通过增加 InAs/In0.11Ga0.89As/GaAs QD 的堆叠数量而减少。因此，我们可以推断，与 Ilahi 等人研究的一层 InAs/InGaAs/GaAs QD 相比，潜在深度的减少提高了结构效率。和赫尔米等人。 [10, 36]。

与温度相关的热重新分布以数字方式确定。特征温度 (T loc/deloc 和 T 逃逸）在定位-离域过程中被指示

研究样本的阿伦尼乌斯拟合。归一化积分强度（黑圈 ) 具有三个活化能（红色实线 )

局域电子/空穴（激子）态 (WL) 的 QD 分布示意图 润湿层，CH 载波传输通道）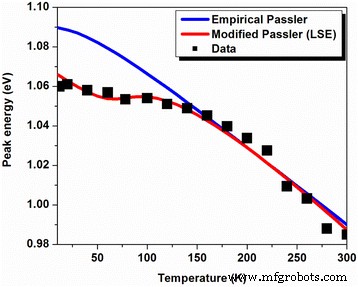

结论

总之，我们通过在 QD 上覆盖 InGaAs 层并插入 GaAs 间隔层，成功地制造了具有多层 InAs QD 的 GaAs 基 SC。在 3 和 4.5 eV 的 InAs/InGaAs/GaAs QD 异质结构的介电函数光谱中观察到的两个主要光谱特征归因于 E 1 和 E 2 GaAs 和 InAs 的 CP 结构，分别。 GaAs 基体中 InAs QD 的 PL 光谱强烈且呈现不对称形状，这表明高质量、多堆叠 InAs QD 结构的生长。还证明了较大和相对较小的 QD 对 PL 光谱的贡献。使用开发的 LSE 模型成功地对发光测量进行建模和重新解释。理论研究定量解释了观察到的温度相关光谱，并基于拟合参数阐明了多层 InAs/InGaAs/GaAs QD 中复杂的自发发射机制。这项研究提出了一种提高 InAs/GaAs QD 结构在光伏应用中使用效率的方法。这些结果有助于提高对应变工程 QD 中温度相关载流子动力学的理解，以提高研究结构的效率。进一步开展这项工作，我们将研究取向的影响以及多堆叠结构的 InAs/GaAs QD 数量的增加对定位深度的影响。