双轴拉伸应变锗纳米线的理论研究
摘要
我们从理论上研究了 GaSb 上的横向高拉伸应变 Ge 纳米线。有限元方法已用于模拟 Ge 纳米线中的残余弹性应变。在不同情况下计算Ge沉积前后的总能量增量,包括应变能、表面能和边缘能。结果表明,在两种情况下,GaSb 上的 Ge 纳米线易于沿 <100> 而不是 <110> 生长,并且在沉积少量 Ge 时更倾向于通过 {105} 面暴露,而被 {110 } 当Ge量超过临界值时。此外,Γ 中的导带最小值 两种情况下任何位置的 -valley 都比 L-valley 中的值低,导致 Ge 纳米线中的直接带隙跃迁。对于价带,Γ 处的光空穴带最大值 点高于任何位置的重空穴带最大值,甚至高于静水应变的导带最小值超过 5.0%,导致负带隙。此外,由于在高拉伸应变下有效质量的减少,可以提高电子和空穴的迁移率。结果表明,双轴拉伸应变Ge纳米线在器件应用中具有良好的性能。
背景
锗 (Ge) 作为 IV 族元素,在光电子学和电子学方面都具有优势,并且与硅 (Si) 光子学具有很好的兼容性。 Ge 的一个基本特性是它的直接带隙约为 0.8 eV (1.55 μ m) 在 300 K。Ge 中电子和空穴的迁移率远高于 Si。因此,Ge 已被用于当前基于 Si 的集成电路中的高速器件 [1, 2]。更有趣的是,拉伸应变 Ge 在上述方面提供了优化。 Ge是一种间接带隙半导体,L-valley和Γ之间的微小差异为136 meV -谷[3]。理论上预测,沿<111> [4] 的单轴拉伸应变超过 4.0% 或双轴 [5, 6] 拉伸应变超过 1.6-2.0% 可以降低 Γ -谷低于L谷,从而将Ge转化为直接带隙材料,这为IV族材料的发光开辟了新途径。另一个重点是张应变Ge显着提高载流子迁移率[7, 8],以实现高速互补金属氧化物半导体器件。
由于大的表面积与体积比以及载流子和光子在二维 (2D) 中的限制,纳米线 (NW) 表现出有吸引力的电子和光学特性 [9]。在过去的几年里,Si 上的 Ge NWs (GeNWs) [10] 或 Ge/Si 核/壳 NWs [11] 由于它们在用于 Si 微电子的金属氧化物半导体场效应晶体管 (MOSFET) 中的潜力而受到广泛研究。与传统的 Si p 相比,缩放的跨导和导通电流均提高了三到四倍 -MOSFET [12]。因此,直接在 Si 上外延生长横向 GeNW 有望制造高性能 MOSFET。张等人。解决了 Si (001) 上的超薄 GeNW 暴露于 {105} [13] 的小平面,其具有最低的预测表面能 [14]。此外,SiGe 虚拟衬底上的应变 Ge MOSFET 被证明可以提高空穴迁移率 [1]。尽管具有压缩应变的 Si 上的横向 GeNW 可以显示出所假设的载流子传输的显着改善,但它们无法转换为直接带隙。为了在 GeNW 中引入拉伸应变,需要 GeSn 合金 [15] 和 III-Sb 化合物 [16],它们具有比 Ge 更大的晶格常数。尽管机械方法已被应用于制造单轴应变 GeNW [17, 18],但这种制造技术的复杂性很难适用于硅基光子学和电子学的单片集成。此外,应变很容易在独立的 NW 中释放,而横向 GeNW 本身可以适应高得多的应变。因此,需要外延生长的具有高双轴拉伸应变的横向GeNWs来实现直接带隙跃迁以及载流子迁移率的增强。
迄今为止,InP (001) 上的无位错和高度双轴拉伸应变的 Ge 量子点已显示出通过有限元方法 (FEM) [19] 模拟的直接带隙发射的潜力。与此类似,在这项工作中,我们从理论上预测了双轴拉伸应变 GeNW 在松弛 GaSb 模板上的暴露表面形态和生长方向,该模板可以直接在带有 AlSb 缓冲层的 Si 上生长 [16, 20]。我们选择 {110}、{105} 和 {111} 作为横向 GeNW 的暴露表面,并比较稳态系统中的总能量变化。为简单起见,我们在这个高度应变的系统中忽略了位错和断裂的影响 [21]。基于 FEM 的模拟表明存在临界量的 Ge。低于临界值,GeNWs 由 {105} 暴露,而高于临界值,它们由 {110} 暴露。几乎所有的 GeNW 区域都可以转换为直接带隙,即在 Γ 处导带最小值和光空穴带最大值的差值 -观点。此外,我们还定性分析了Γ处应变相关载流子有效质量的变化。 -指向间接预测电子和空穴迁移率的增强。
方法
横向 NW 通常显示三角形横截面 [22, 23]。由于图 1a 所示的 NW 的一维特性,类似于 Zhang 等人的有限 NW 模型。在参考文献的补充材料中。 [13]可以适当地用于模拟,其中开始和结束的表面都是固定的,如图1b所示。由于边界效应,我们只讨论 NW 的中心部分,并认为这部分的横截面代表了无限长 NW 中的情况。 FEM 用于模拟与 GaSb 有 7.7% 晶格失配的 GeNW 中的拉伸应变分布。我们计算在三种情况下在稳态下沉积相同数量的 Ge 后的总系统能量增量:(i)[100] 生长方向,{110} 面暴露(情况 A),(ii)[100] 生长方向,但{105}面暴露(情况B),和(iii)[110]生长方向,{111}面暴露(情况C)。这三种情况的横截面如图 1c 所示。横截面面积保持不变,代表等量的Ge。
<图片>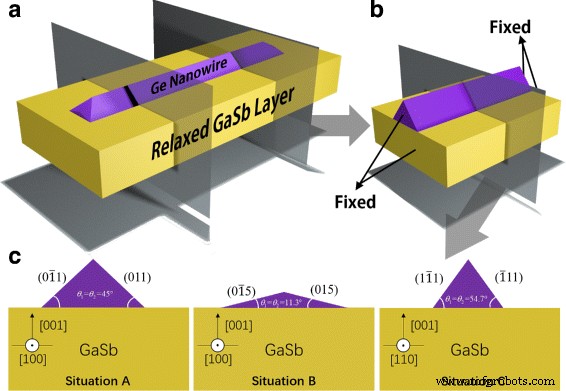
GaSb 上的 GeNW 示意图:a 3D 模型,b 简化的有限模型和 c 不同面的GeNW横截面
每单位长度的系统总能量变化 (J/nm) 包括应变能、表面能和边缘能的整体差异 [24],可由下式给出:
$$ \Delta{{E}_{\text{total}}}=\Delta{{E}_{\text{strain}}}+\Delta{{E}_{\text{surface}}}+ \Delta{{E}_{\text{edge}}}。 $$ (1)第一项Δ E s t r 一 我 n 表示Ge沉积前后稳态系统的应变能差,以单位体积表示,
$$ \Delta{u}=\frac{1}{2{Y}}\sum\limits_{i=j}^{{}}{\tau_{ij}^{2}}-\frac{\nu {Y}\sum\limits_{i其中 h 是 GeNW 截面的高度,σ 我 (i =A、B、C)为单位面积下暴露面的平均表面能,NW面与界面的对应夹角用θ标记 我 如图 1c 所示。表面能的应变可以忽略不计,因为它对参考文献中的处理影响很小。 [25]。表 1 显示了文献中的表面能值。最后一项称为边缘能量变化代表形成锐利边缘的能量成本的变化,由
给出 $$ \Delta{{E}_{\text{edge}}}=3\varGamma $$ (4)其中 3Γ 是包含顶部和两个基底面交点的总边缘能量。通过实验拟合 [26] 估计 3Γ 的值为 3.7 eV/nm,由于值几乎没有变化,边缘能量的影响可以忽略不计 [25]。因此,计算Δ的能量增量是有效的 E 总计−3Γ。
知道应变分布后,应变相关导带在 Γ 处减少 - 并且可以在忽略量子效应的情况下计算 L 谷。 Γ 的导带 - 山谷仅在静水应变下降低
$$ \Delta E_{c}^{\Gamma}={{a}_{c}}({{\varepsilon}_{xx}}+{{\varepsilon}_{yy}}+{{\varepsilon }_{zz}}) $$ (5)其中 a c 表示在 Γ 处具有 -8.24 eV 值的静水变形势 -点[27],ε xx , ε yy 和 ε zz 是 x 中的应变 , y, 和 z 分别在材料坐标系中的方向。然而,导带在 L 点的位移受流体静力和剪切应变的影响 [19],由
给出 $$ {{}\begin{aligned} \Delta{E_{c}^{\mathrm{L}}}=&\left({{\Xi}_{d}}+\frac{1}{3} {{\Xi}_{u}}\right)({{\varepsilon}_{xx}}+{{\varepsilon}_{yy}}+{{\varepsilon}_{zz}})\\&-\frac{2}{3}{{\Xi}_{u}}\left(|{{\varepsilon}_{xy}}|+|{{\varepsilon}_{yz}}|+|{ {\varepsilon}_{xz}}|\right) \end{aligned}} $$ (6)其中 Ξ d 和 Ξ 你 分别是 L 谷处的膨胀变形势,值为-6.97 eV,单轴变形势为 16.3 eV。为了将 Ge 转化为直接带隙材料,Γ -valley 必须低于 L-valley,这意味着 \(\Delta {E_{c}^{\Gamma, \text {L}}}=\Delta E_{c}^{\Gamma }-\Delta {E_{c}^{\mathrm {L}}}<-0.136\) eV。这里,我们使用 \(\Delta {E_{\text {DT}}}=\Delta E_{c}^{\Gamma, \text {L}}+0.136\) 来表示 Γ - 和 L 点。一旦Γ - 点下降到 L 点以下,Δ E DT 将为负数。模拟一系列不同尺寸的拉伸应变GeNWs,以显示直接带隙跃迁。
此外,由于 GeNW 中的高拉伸应变,Γ -valley 低于 L-valley,而轻空穴带最大值变为价最大值 [28]。如此高拉伸应变的 GeNW 中的带隙将是 Γ -valley 和 Γ 处的光孔带最大值 -观点。因此,空间分布的带隙以及 Γ 处的带边缘能量 - 点是 k =0 包括导带、重空穴带和轻空穴带由八波段k.p计算 理论 [29]。我们忽略了量子效应,因为它在我们的 GeNW 模型中非常弱,具有 40 纳米的基础宽度。该结果可用于研究拉伸应变 GeNW 中的电子-空穴复合以及迁移率增强的机制。通常,电子或空穴迁移率可以由 μ 给出 =e τ /米 * , 其中 m * 是载流子有效质量和 τ 是电子-声子散射时间。在 Γ 的抛物线近似模型中 - 和各向同性散射的L-valleys,散射时间与\(m_{DOS}^{*-3/2}\)成正比,得出迁移率比达到μ的结论 Γ /μ L=182 如果 Γ -valley 移动到 L-valley 以下,并且电子-声子散射时间和电子的有效质量都随应变不变 [30]。然而,考虑到在我们的 NW 模型中计算各向异性散射和应变相关有效质量的复杂性,我们只定性地分析了通过减少两个电子和高张力 GeNW 中电子和空穴迁移率的改善。和 Γ 处的空穴有效质量 -点。
结果和讨论
由于 Ge 和 GaSb 之间 7.7% 的大晶格失配,我们认为系统最初处于完全拉伸应变。图 2 显示了包含面内应变 ε 的二维残余应变分布 xx , 剪应变 ε xy , 和垂直应变 ε zz 基本宽度为 w 的情况 A =40 nm 例如在弛豫后的稳态中。这里的应变定义是 (a 格斯-a Ge)/a 哥,其中a Ges 和 a Ge 分别是应变和松弛 Ge 的晶格常数。如图 2a 所示,ε xx 两个基底边缘的最大值约为 15.4%,远大于初始应变,但从边缘到中心急剧下降,最小值约为 3.3%。在 z - 从 GeNW 底部到顶部的方向,ε xx 也由于 GeNW 的松弛而下降。 ε的分布 zz 发现与 ε 具有相似的特征 xx 在图 2b 中。与 Ge 薄膜中的双轴应变不同,图 2c 显示 GeNW 的不对称分布的剪切应变分量在直接带隙跃迁中起着重要作用。三种情况下的应变分布非常相似。然而,由于宽高比(W /H ) 由其形状引起。由 {105} 表面暴露的 GeNW 的情况 B 具有最大的 W /H 10,表现出与Ge薄膜相似的高应变。 {111} 表面暴露的情况 C 也显示出高应变,因为沿 [110] 的 NW 生长方向保持不变的应变值,提高了 ε 的值 xx 和 ε yy 同时。因此,面内应变几乎不能松弛。
<图片>
基宽为 40 nm 的情况 A 下 GeNW 的残余应变分布:a x分量应变ε xx , b z分量应变ε zz , 和 c x-y 平面中的剪切应变 ε xy .底部的锯齿形表示部分基板层(下同)
根据应变分布,可以获得应变能增量。如前所述,情况 B 的应变能增量最高,而情况 A 的应变能增量最低。然而,对于表面能变化,情况 B 给出的负值随着横截面面积的增加而减小,而其他两种情况在同一面积下显示出非常接近的正值。不包括边缘能量变化的总能量增量如图 3a 所示。结果表明,由于能量增量从来都不是最低的,因此仅在情况 C 中不太可能形成 GeNW。随着面积的增加,能量增量有两种不同的结果,标出垂直虚线表示面积的临界值,A c =136.2nm 2 , 表示 Ge 的数量。当面积小于 136.2 nm 2 , GeNWs 倾向于在情况 B 中形成形状,但在沉积更多 Ge 后在情况 A 中。计算结果预测 GaSb 上的拉伸应变 GeNWs 可能更喜欢形成高 W /H 当沉积少量 Ge 时横截面呈三角形,而形成低 W /H 超过临界值后之一。图 3b-e 显示了临界区域下 A 和 B 情况下静水应变的分布和剪切应变分量的绝对值之和。将情况 A 与 B 进行比较,尽管情况 A 拥有更大的静水应变和 |ε 的最大值 xy |+|ε yz |+|ε xz |,情况B具有较大的平均静水应变,但|ε的平均值较小 xy |+|ε yz |+|ε xz |。同时,情况 B 表明静水应变和 |ε 的空间分布存在微小差异 xy |+|ε yz |+|ε xz |。这些特性与锗薄膜非常相似,归因于它的高W /H 价值。因此,参考方程。 (5)和(6),情况B表现出较小的Δ值 E DT 比情况 A 大,导致 Ge 转化为直接带隙材料的可能性很大。
<图片>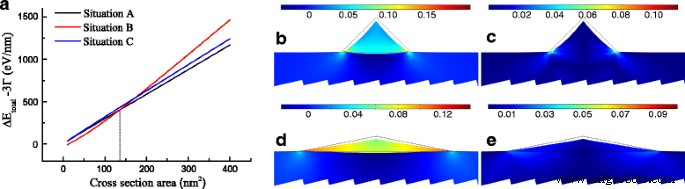
一 不包括边缘能量变化的总能量变化 3 Γ 与横截面积(虚线 是关于 136.2 nm 2 的最小值的临界值 在不同的情况下)。 b –e 静水应变和 |ε xy |+|ε yz |+|ε xz |在 b , c 情况 A 和 d , e 情况B处于临界值
由于 GeNW 中的高拉伸应变,几乎所有 GeNW 区域都可以转换为直接带隙。图 4a 显示了 Δ 的分布 E DT 随着 GeNW 的大小增加。 Δ的值 E DT 在 GeNW 中从顶部下降到底部。有趣的是,Δ 的最小值 E DT 在情况 B 中位于横截面的底部边缘,但在情况 A 中位于底部中心。 这种不同分布的原因是情况 A 中底部边缘的显着剪应变对 \(\Delta E_{c}^{\mathrm {L}}\) 比情况 B. 对于情况 B 低于临界区域的 GeNW,平均 Δ E 如图 4b 所示,DT 远低于临界区域上方的情况 A。在临界点,Δ的平均值 E DT 突然从 -0.308 的值上升到 -0.137 eV。此外,对于相同的形状,Δ的分布和平均值 E DT 基本相似,与大小没有明显关系。为了发现与 GeNW 中应变的内在关系,我们在图 5 中绘制了 GeNW 基底处具有基底宽度的静水应变分量。不同尺寸的静水应变分量与 GeNW 中基底相对位置的曲线除了外围区域的差异外,几乎重叠。在 ε 中发现了一致的结果 xx 和绝对剪切分量的总和。因此,Δ的应变诱导值 E DT在相同形状的GeNW中具有相同的分布。
<图片>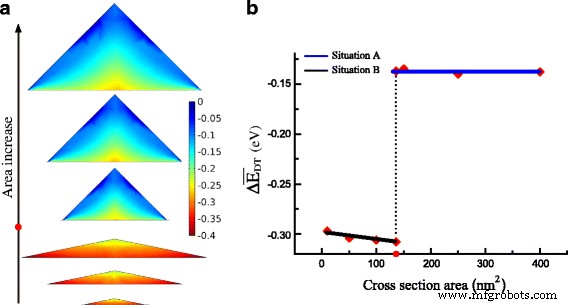
一 Δ的分布 E DT 随着面积的增加(颜色条 表示Δ的值 E DT)。 b Δ的平均值 E DT 与面积。临界值用红点标记 在区域轴上
<图片>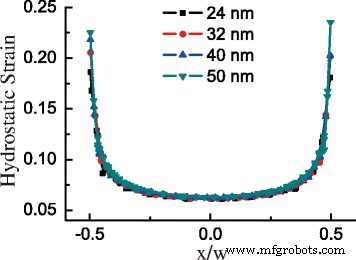
不同基宽下GeNW基部静水应变分量vs.x/w
此外,我们模拟了图 6a 所示的 40 nm 宽 GeNW 横截面中的应变诱导带隙映射。带隙的空间分布由Γ处应变相关带边的变量值推导出来 -观点。图 6b 展示了 Γ 处的带边能量 - 沿 z 点 -GeNW 的方向。我们发现导带和价带边缘(包括轻空穴带和重空穴带)在前 15 nm 内发生显着变化,然后略有变化。随着拉伸应变的增加,轻孔带和重孔带的顶部分开并倾向于向相反的方向移动。从图 6a、b 可以看出,带隙在前 15 nm 显着增加,达到约 0.30 eV,然后在 0.24 eV 附近略有变化,这是大多数 GeNW 区域的带隙。由于在 Γ 处,轻空穴带的最大值高于重空穴带的最大值 在 GeNW 中,价带中的空穴更倾向于位于轻空穴带最大值处。因此,电子-空穴复合将发生在导带最小值和光空穴带最大值之间的 Γ -point 如果我们忽略依赖空间的电子和空穴波函数的重叠。有趣的是,在图 6a 中标记为黑色曲线的 NW 底部区域中,轻空穴带最大值甚至高于导带最小值,静水应变超过 5.0%。我们在高拉伸应变下计算的负带隙可能会导致复杂的后果,如半金属[31]或倒[32]能带结构。
<图片>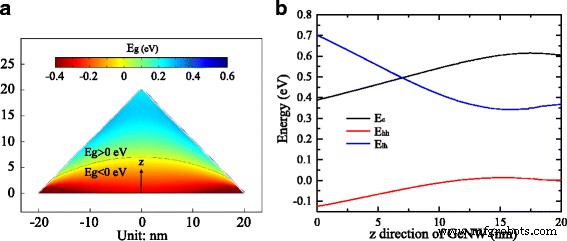
一 GeNW 中应变相关的带隙按位置分布。 b 沿 z 的应变相关能带边缘能量 GeNW 方向
最后,在 GeNW 中如此高的拉伸应变下,电子和空穴的迁移率将得到增强。对于弛豫的 Ge,电子传输主要由位于 L 谷的电子贡献。当 Ge 处于拉伸应变下时,Γ -valley 低于 L-valley,如图 3a 所示,电子传输的主要贡献来自 Γ -谷。另一方面,空穴在传输中的主要参与来自 Γ 处的光空穴带 -点在高拉伸应变下,而重空穴带在松弛情况下占据价带最大值。由于 Γ 处的电子有效质量小得多 -点比L点,以及从重空穴带最大值到轻空穴带最大值的减少的有效质量,不仅电子而且空穴的迁移率都可以增强。理论上可以预测拉伸应变以减少 Γ 处的电子和空穴的有效质量 - 指向 Califano 的量子点模型 和哈里森 [29]。尽管定量计算方法不适用于我们的 NW 模型,但我们定性地假设拉伸应变可以修改 k 处的有效质量 =0 通过增加小 k 的色散关系曲率 在Γ附近 -观点。因此,在拉伸应变的 GeNW 中可以增强电子和空穴的迁移率。分裂的价带还引起强烈的电子-声子耦合和带内散射[33],这限制了空穴迁移率低于电子迁移率。
结论
总之,我们在 GaSb 上提出了拉伸应变的 GeNW,通过 Ge 沉积前后的总能量变化比较了三种不同的情况。结果表明,在临界量之前,GeNW 倾向于沿着〈100〉生长方向形成 {105} 面,而在临界量之后由 {110} 面暴露。残余应变场和带隙分析表明,相同形状的应变和Δ具有相似的分布 E DT 不分大小。此外,面内应变和流体静力应变不仅从边缘到中心减小,而且在所有情况下也从底部到顶部减小。由于高拉伸应变,在两种可能的情况下,几乎整个 GaSb 上的 GeNW 都可以转化为直接带隙材料。此外,光空穴主要参与Γ处的电子-空穴复合和电传输。 点,因为轻空穴带最大值在高拉伸应变下变成价带的最大值。由于Γ处载流子有效质量的降低,不仅电子而且空穴的迁移率都可以提高 -点由拉伸应变决定。理论上预测的有吸引力的性能意味着拉伸应变的GeNWs有望分别应用于光源的光电子学和Si光子学和电子学中高速器件的微电子学。
纳米材料


