由圆偏振光驱动的等离子体二聚体的自旋和轨道旋转

背景

线性偏振 (LP) 光照射下的两个微粒 (MP) 或纳米粒子 (NP) 的光学结合是一种重要的光机械行为，它是光与物质相互作用的结果 [1,2,3,4]。光学结合的二聚体之间有几个稳定平衡的粒子间距离；这些距离几乎是介质中波长的整数倍 [3,4,5,6]。此外，二聚体的方向垂直于 LP 光的偏振。由于粒子间距离接近波长的整数倍，粒子之间的散射光子产生相长干涉以产生结合力。还研究了多个二氧化硅 MP 或 Ag NP 的光学结合阵列现象 [7,8,9,10]。对于圆偏振 (CP) 平面波的照明，Haefner 等人。据报道，两个尺寸为 100-700 nm 的耦合二氧化硅 NP 的纵向自旋和轨道旋转的螺旋度与入射光的旋向性相同 [11]。最近，Sule 等人。实验发现，受光力束缚的两个半径为 75 nm 的 Ag NP 的轨道旋转的螺旋度与水中 790 nm 聚焦 CP 高斯光束的旋向性相反 [12]；即，Ag 二聚体的光学轨道扭矩为负 [13, 14]。此外，测得的轨道旋转约为 4 kHz [12]。另一方面，还研究了由 CP 高斯光束引起的半径为 100 nm 的单个 Au NP 的自旋 [15,16,17,18]。测得的自旋旋转高达 3.5 kHz [15]。近几十年来，光场的纵向/横向自旋轨道耦合（SOC）引起了很多关注[19,20,21,22,23]。例如，光学涡旋光束（例如，具有方位角或径向偏振的高阶拉盖尔-高斯光束）或高度聚焦的 CP 高斯光束可用于诱导 SOC [24,25,26,27,28,29,30 ,31,32,33,34]。光学涡旋光束的扭曲电磁 (EM) 场携带自旋角动量和轨道角动量，从而诱导附近探测 NP 的纵向/横向自旋和轨道旋转 [18,19,20,21,22,23 ,24,25,26]。特别是，由于这些纳米颗粒中自由电子的集体运动（等离子体效应），Au 或 Ag 纳米颗粒近场中的 SOC 更为显着 [28,29,30,31]。

在本文中，我们从理论上研究了由 CP 高斯光束照射引起的由基板支撑的两个耦合 Au NP（二聚体）的光机械行为（光力和扭矩）。基板是必要的，以限制这些独立的 NP 在焦平面中移动，而不是漂浮在 3D 空间中。多极 (MMP) 方法用于数值模拟 EM 场，然后分析光学束缚二聚体上的光学轨道和自旋扭矩 [35, 36]。通过二聚体的光机械响应，将表现出纵向/横向 SOC。尤其是在二聚体上产生负光学轨道扭矩的条件也将被研究。

方法

图 1 显示了一对相同的 Au NP 由基板支撑并由垂直入射左手 (LH) CP 光（平面波或高斯光束）照射的配置，其中 d 表示粒子间距离。高斯光束的腰部用w表示 0，焦平面位于 Au NPs 的中心横截面。平面波和高斯光束的电场公式见附件。我们假设基材的折射率与周围介质水的折射率相同。因此，反射光不会在介质与基板的界面处被感应；光场不受基底存在的干扰 [37]。另一方面，衬底的存在作为限制来支持纳米粒子在衬底上移动。多极（MMP）方法用于模拟感应电磁场 [17, 18, 35, 36]。光学力 F ^j 施加在 j 第 NP (j =1, 2) 表示为

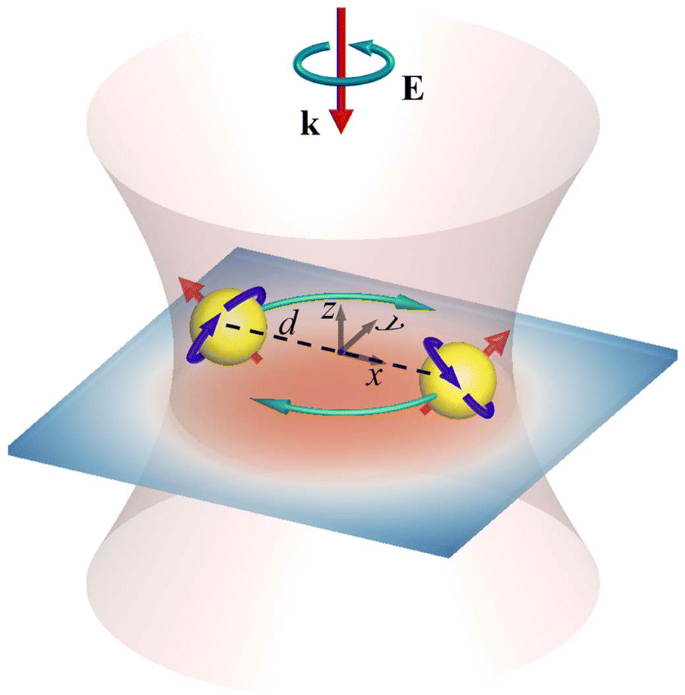
一对带有支撑基板的 NP 的配置，由腰部的垂直入射 LH CP 高斯光束 (w0) 照射。这些纳米颗粒的中心截面位于高斯光束的焦平面上，d 是纳米颗粒中心之间的距离。光机械响应为纵向轨道旋转和纵向/横向自旋

在这里，n 是 j 表面的外向法向量 第 NP 和 T 是时间平均麦克斯韦应力张量，表示为

$$ \mathbf{T}=\frac{1}{2}\operatorname{Re}\left\{\varepsilon \mathbf{E}\overline{\mathbf{E}}+\mu \mathbf{H}\ overline{\mathbf{H}}-\frac{1}{2}\left(\varepsilon \mathbf{E}\cdot \overline{\mathbf{E}}+\mu \mathbf{H}\cdot \overline {\mathbf{H}}\right)\;\mathbf{I}\right\}。 $$ (2)

在方程式中。 (2)、我 是一个 3 × 3 单位矩阵，overbar 表示复共轭，Re 表示实部 [17, 18, 35, 36]。这里，ε 和 μ 是周围介质的介电常数和磁导率。请注意，E 和 H 是用于方程的外部总场。 (2).事实上，T 也是时间平均的线性动量通量。在整篇论文中，光学力用柱坐标表示：径向、方位角和 z - 轴组件。径向力可以判断两个纳米颗粒之间的吸引力或排斥力，方位力可以判断纳米颗粒轨道旋转的螺旋度。

另一方面，j 上的光学自旋力矩 第 NP (j =1, 2) 对于单个 NP 的旋转由下式给出，

$$ {\mathbf{M}}^j={\int}_{S_j}{\mathbf{x}}^j\times \mathbf{T}\cdot \mathbf{n}\;\mathrm{d} S。 $$ (3)

在方程式中。 (3)、x ^j × T 是角动量通量和 x ^j 是点 x 的相对位置向量 在表面 S j 相对于 j 的质心 \( {\mathbf{x}}_c^j \) 第 NP； \( {\mathbf{x}}^j=\mathbf{x}-{\mathbf{x}}_c^j \)。纵向被指定为平行于光轴（比如 z 方向），横向与光轴垂直。另一方面，z 中的纵向光学轨道扭矩 由方位角光力引起的每个 NP 上的方向定义为 F θ d /2 在圆柱坐标系中。 λ处Au的相对介电常数 模拟中使用的 =800 nm 是 (− 24.062, 1.507) [38]。

结果与讨论

我们研究了由垂直入射的 LH CP 平面波或焦平面上的聚焦高斯光束照射的半径为 100 nm 的两个相同 Au NP 上的光学力和扭矩。周围介质是水。中心平面波或高斯光束的通量为 25 MW/cm ² .由虚拟基板支撑的两个独立 NP 的中心允许在 xy 平面（焦平面）。光学力 (F r , F θ ) 与粒子间距离 d 对于 CP 平面波或束腰为 500 nm λ 的聚焦高斯光束 =800 nm 分别显示在图 2a、b 中。这些 NP 的中心横截面位于高斯光束的焦平面上。图 2a 表明对于平面波，有几个稳定平衡的粒子间距离与 F r =0 且为负斜率；第一个 d 1 在 603 nm，第二个 d 2 在 1204 纳米。这些“稳定平衡”的粒子间距离几乎是介质中波长的整数倍；即，d 米 =mλ /n , 其中 n 是介质的折射率，m =1, 2, 3... 是光结合力引起的长程光-物质相互作用的结果。这表明存在连接两个 NP 的光学弹簧；恢复力F r 光学弹簧在这些稳定平衡的粒子间距离处使 NP 彼此分开。对于高斯光束，前两个稳定平衡粒子间距离 d 1 和 d 2 分别为 585 和 1131 nm，如图 2b 所示，由于高斯光束引起的梯度力，略小于平面波。

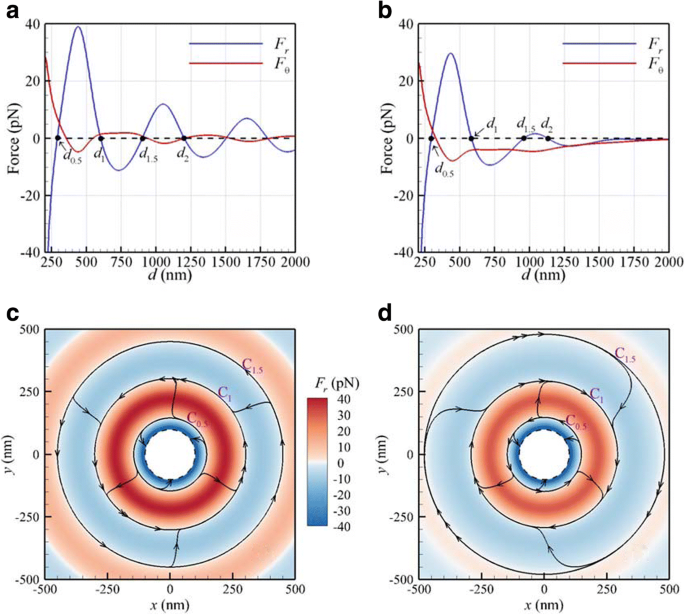
光学力 (F r , F θ ) 与 d 对于 λ CP a =800 nm 平面波和b 焦平面上束腰为 500 nm 的高斯光束。光力的二维流线图 (F r , F θ ) 由 CP c 诱导 平面波和d 高斯光束。颜色条代表F的幅度 r .虚线环是两个NP接触的NP中心的极限圆

事实上，纵向轨道力矩F θ d /2 将驱动这些 NP 在直径为 d 的轨道上旋转 1 和 d 2. 对于高斯光束的情况，轨道将以光束轴为中心。方位角光学力的符号 (F θ ) 表明高斯光束引起的第一稳定平衡轨道的纵向轨道旋转（公转）与平面波相反。这表明负 F θ CP高斯光束产生负轨道力矩F θ d 1/2 在第一个稳定平衡轨道；更重要的是，Au 二聚体轨道旋转的螺旋度与入射 CP 光的旋向性相反 [12]。值得注意的是，F θ d 总是负数> 300 nm 对于高斯光束的情况；在光镊系统中很容易观察到由于负轨道扭矩导致的光学束缚 NP 的反向旋转（旋转）现象。负的光学轨道扭矩可能归因于高斯光束的扭曲电磁场[23]。

根据由力 F 驱动的球体的斯托克斯定律 在粘性流体中移动，终端速度 v T 是 v T =F /(6πrη )，其中 η 是水的动态粘度 (0.001 kg/m s)。这是施加的力被粘性流体的阻力平衡的结果 [39]。根据斯托克斯定律，粘性介质中 NP 的终端速度矢量与施加的力成正比 [39]。因此，我们使用光力场来获得流线，这几乎等同于这些 NP 的轨迹。此外，直接从光力矢量场 (F r , F θ ) 施加在 NPs 上绘制在图 2c，d 分别为平面波和高斯光束，其中颜色条代表 F 的幅度 r .请注意，流线在每个点的切线然后平行于光力矢量，因此也平行于 NP 的速度。对于小的粒子间距离范围 (d <d 0.5)，径向光力F r 为负，因此这两个 NP 最终会相互吸引而发生碰撞，如图 2c、d 所示。虚线环是两个 NP 中心的极限圆，其中 NP 接触。内环（蓝色）是短程相互作用的区域。内圈C 内环之间的 0.5（蓝色，带有负 F r ) 和第二个环（红色，带有正 F r ) 是 Au 二聚体的短程和长程相互作用区域之间的边界线； C 的直径 0.5 是 d 图 2c 和 d 中的 0.5 =291 nm 图 2d 中的 0.5 =296 nm。在远距离 (d 0.5 <d <d 1.5），径向和方位角的光力驱动两个耦合的NP接近第一个稳定平衡轨道C 1 直径 d 1 由于光学结合力的影响。光学束缚的金二聚体沿轨道 C 逆时针 (CCW) 旋转 1 (d 1 =603 nm) 在图 2c 中，而沿着 C 1 (d 1 =585 nm) 在图 2d 中顺时针 (CW)。前者的旋转与正轨道力矩(F θ> 0)，后者由于负轨道力矩(F θ <0)。根据我们对 CP 平面波（此处未显示）照射的稳定平衡距离为 603 nm 的二聚体的散射截面光谱的分析，光学束缚二聚体的耦合表面等离子体共振 (SPR) 几乎在800 nm 对应于入射光，这是单个 NP (530 nm) 的偏共振。一般来说，二聚体的耦合 SPR 取决于粒子间距离；距离越大，二聚体的耦合 SPR 越红移。如果我们使用更长波长的高斯光束（例如 1064 nm），则稳定平衡粒子间距离会增加。然而，随着两个NPs之间的距离变得过大，光耦合效应减弱，耦合SPR逐渐消失。因此，单个 NP 在 530 nm 处的 SPR 成为主导。

对于沿直径为 d 的轨道移动的半径为 100 nm 的 Au NP 和角速度Ωz，速度为Ωzd /2 =F θ /(6πrμ ）。如果应用高斯光束 (F θ =− 4 pN)，沿 C 的角速度 Ωz（每秒周期数） 1 大约是 − 7 kHz。量级与实验结果一致[12]； r 的两个 Ag NPs 的轨道旋转角速度 =75 nm 由 14 mW 的高斯光束照射为 − 4 kHz。如果 d 1.5 <d <d 2.5，这些纳米粒子将沿着二级稳定平衡轨道C靠近并旋转 2（此处未显示）。请注意，对于这些情况，F 的光力 z 由于辐射压力，将这些 NP 推向下游是负面的； F z =− 161.3 pN（平面波）和 − 117.2 pN（高斯光束）。这推断来自支撑基板的反作用力是平衡 F 的驱动光力所必需的 z .因此，z 中的合力 这些 NP 的方向为零；这两个 NP 被限制在 xy 中移动 焦平面的平面。

另一方面，图 3a、b 显示了光学自旋扭矩 (M r , M θ , M z ) 与 d 分别由焦平面上的平面波和高斯光束引起。由于这两个 NP 的结果是相同的，这里只绘制了一组光学自旋力矩。前两个（M r , M θ ) 是横向自旋力矩，后者 M z 是纵向的。发现在这两种情况下，纵向自旋扭矩的螺旋度与入射光的旋向性相同。这是因为入射 CP 光的吸收光子的角动量被转移到这些 NP 以进行自旋和轨道旋转。值得注意的是，横向光学自旋力矩 (M r , M θ ) 由高斯光束引起，与平面波相比要大得多。这可能归因于高斯光束焦平面处扭曲的 EM 场的横向分量。此外，光学横向自旋扭矩的最大值大致出现在第一稳定平衡轨道C 1 (d 1 =585 nm)，如图 3b 所示。根据斯托克斯定律，旋转球以扭矩 M 旋转 在粘性流体中，球体的终端角速度为ω T =M /(8πr ³ μ ) [18]。因此，NP 在 C 处的纵向/横向自旋角速度的大小 1 约为 10 kHz，其数量级与测得的纵向自旋速度 [15] 一致，约为 3.5 kHz。综上所述，如上图所示。图 2b 和 3b 表明纵向轨道旋转伴随着纵向/横向自旋。两个耦合的纳米粒子的运动类似于双星系统的运动，其中光学力为这些纳米粒子提供束缚力和轨道驱动力，光学自旋力矩导致它们自旋。

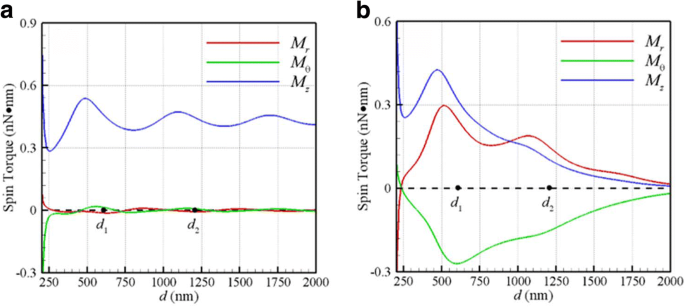
光学自旋力矩 (M r , M θ , M z ) 与 d 在 λ a =800 纳米 平面波和b w 的高斯光束 0 =500 nm 焦平面

此外，还可以通过调整光镊物体的光圈来改变入射光束的大小，从而改变高斯光束的数值孔​​径和腰围。图 4a 显示了光学轨道扭矩 F θ d /2 在半径为 100 nm 的两个耦合 Au NPs 上在相应的第一稳定平衡轨道 (d =d 1) 与λ的CP高斯光束的腰部对比 =800nm。对应的第一稳定平衡距离d 图 1 也绘制在图 4a（右侧的比例尺）中，其中平面波可以视为 w 的特殊情况 0 → ∞。正负轨道扭矩之间的高斯光束腰部的转折点在 1150 nm，对应于 F θ =0，如图 4a 所示。高斯光束的束腰越小，负轨道扭矩的幅度越大。随着腰围的增加，d 高斯光束的 1 接近平面波 (w 0 → ∞）。特别是，随着腰部的减小，横向自旋扭矩的大小 (M r , M θ ) 在 d 1 显着增加，而纵向自旋力矩M z 减少，如图 4b 所示。这些结果说明高斯光束的束腰是由于电磁场畸变程度而引起负的纵向轨道力矩和横向自旋力矩的关键因素。

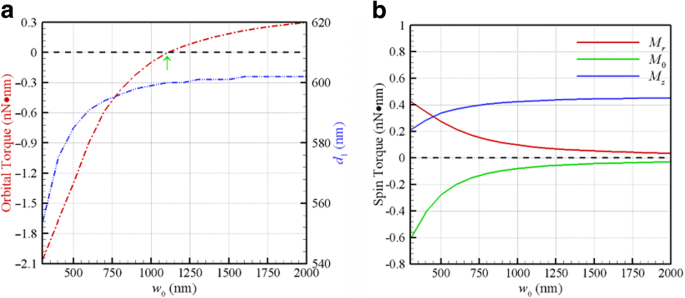
一 光学轨道扭矩和d 1 在第一个稳定平衡轨道与 λ 的高斯光束束腰 =800nm。产生正或负轨道扭矩的腰部的转折点是 1150 nm。 b d 处的光学自旋扭矩与腰部的关系 1

即使没有光束轨道角动量的贡献，这些 NP 的负轨道旋转和横向旋转的机制也可以归因于光场自旋角动量的卷曲 [23]。通过负纵向轨道扭矩和横向自旋扭矩对 Au 二聚体的表现，可以体现光子的等离子体增强 SOC。此外，二聚体的轨道旋转方向和单个NP的自旋取决于入射光的旋向性。

结论

从理论上研究了一对由 CP 光照射的 Au NPs 的光机械响应（光力和扭矩）。我们的结果表明，它们的旋转（公转）的稳定平衡轨道可以被诱导用于长程相互作用；稳定平衡粒子间距离几乎是介质中波长的整数倍。方位角光学力引起这些纳米粒子的轨道旋转，而光学自旋力矩引起它们的旋转，尤其是横向分量。这种运动类似于质量相等的双星在围绕它们共同质心的圆形轨道上运动。当高斯光束的腰部小于转折点时，光学束缚的 Au 二聚体轨道旋转的螺旋度与入射 CP 光的旋向性相反。此外，随着高斯光束束腰的减小，纵向/横向 SOC 变得显着；因此，两个 NP 的横向自旋变得更加深刻。对于短程相互作用，光力引起相互吸引。因此，两个耦合的等离子体 NP 不仅旋转，而且以螺旋轨迹旋转，最终会发生碰撞。此外，两个耦合 NP 的长程和短程相互作用之间的粒子间距离的边界大致在介质中的半波长处。我们的结果表明，光力的数量级约为 pN，可以将其与其他力（例如有质动力）进行比较，以确定对 NP 运动的贡献。我们的发现可能为 SOC 在用于纳米科学和纳米技术的光操纵 NPs 上的应用铺平道路。此外，值得研究两个NPs上的光学自旋和轨道扭矩与EM场的自旋和轨道角动量密度之间的相关性;前者由 \( \operatorname{Im}\left(\overline{\mathbf{E}}\times \mathbf{E}\right)/2\omega \) 定义，后者在参考文献中显示。 [23]。此外，超材料扭曲近场中的SOC值得研究[40,41,42,43]。

缩写

CP：

圆偏振

EM：

电磁

左侧：

左撇子

LP：

线偏振

MMP：

多个多极

MP：

微粒

NP：

纳米粒子

SOC：

自旋轨道耦合