锂离子电池纳米粒子电极快速变形化学势的发展表达式

介绍

为了便携式电子设备、电动汽车和大规模储能的发展，提出了将在锂化过程中体积发生剧烈变化的硅等一些高容量电极材料应用于锂电池中[1,2] ,3]。由均匀体积变形引起的应力称为扩散应力，在循环充放电过程中可能引起脆性断裂，这种负面影响进一步降低了电池的容量[4]。锂离子电池电极的复合材料一般比较复杂，而且它们的形貌也各不相同，这使得用理论或方程来解释电池行为变得更加困难。在理论模型中，通常考虑电极材料参数在空间坐标上的变化来模拟复合材料的性能，而忽略复合材料的界面效应。目前，理论模型主要考虑三种典型的电极形状，即球形、圆柱形和板形。其中，球形和圆柱形通常是一维模型，板电极的一维和二维模型都有。最近，许多研究集中在锂离子电池硅纳米粒子电极中的扩散诱导应力。例如，杨等人。 [5] 提出了一个化学机械模型来研究锂化诱导的相变、形态演变、应力产生和晶体硅纳米线的断裂。李等人。 [6] 研究了局部速度对硅纳米粒子电极中扩散诱导应力的影响。赵等人。 [7] 考虑了主体材料的非弹性变形，分析了扩散诱导应力。在上述所有这些工作中，所涉及的基本物理学是在多种驱动力下固体中的原子或离子扩散。固体中的原子扩散可能会改变固体成分的化学计量状态，并受到扩散诱导应力的影响。这种应力和扩散相互作用受固体热力学平衡的支配。

Larche 和 Cahn [8] 为多组分固体开发了一个热力学框架，该框架在非静水应力下达到平衡。该框架基于成分变化引起的变形小且各向同性的假设。因此，引入了与应力相关的化学势来解释应力和扩散之间的相互作用。 Wu [9] 推导出不同的应力依赖化学势，其中涉及 Eshelby 动量张量而不是静水柯西应力。在此基础上，崔等[10]提出了一种用于固体有限变形的新化学势。然而，在这些作品中，只有在变形很小或变形率与扩散相比足够低时才需要严格推导。硅电极在快速锂化时，由于其成分体积膨胀较大（∼ 400%），很可能导致显着误差。

在本文中，我们提出了一种不假设低变形率的化学势的发展表达式，区别于崔 [10] 的传统表达式。该模型是为电极在充电或放电过程中的快速变形而建立的，并且与形态无关，因为化学势是一个密集量而不是一个广延量。在 Si 纳米粒子电极的恒电位和恒电流操作下，分析了这两种化学势在应力分布和锂浓度分布上的差异。结果表明，差异随着变形率的增加而增加。同时发现了一个临界半径，即在大部分锂化过程中，这两种化学势表达引起的锂通量与柯西静水应力没有差异。

方法

力学方程

将锂插入电极会引起体积变化。为方便起见，我们采用两种方法来描述固体的变形和运动，即拉格朗日描述和欧拉描述。物质粒子在连续介质中的运动可以描述为

其中 x 是欧拉坐标，X 是拉格朗日坐标，U 是位移场。连续体形状的变化可以用变形梯度张量来表征，由下式给出

其中 Grad 表示拉格朗日描述中的梯度算子，I 是二阶单位张量。

对于球状粒子，球系中一个质点的拉格朗日坐标和欧拉坐标分别为(R, θ, Φ)和(r, θ, φ)。然后，变形梯度张量F 被发现为

在充电或放电过程中，电极的形状变化可分为两个过程：（a）由于锂的插入而引起的形状变化和（b）可逆的弹性变形。这两个变形过程可以用两个分离的梯度张量来描述，总变形梯度张量可以写成

其中 F ^e 表示弹性变形，F ^c 表示由于插入锂而导致的形状变化。方程（4）表示电极材料从初始（未变形）状态到当前（变形）状态的过程。假设由于嵌入锂而导致的形状变化是各向同性的，F ^c 可以通过

其中Ω代表偏摩尔体积。

从方程。 (3-5)、弹性变形梯度张量F ^e 是

总格林-拉格朗日应变张量 E 可以写成

其中弹性应变张量 E ^e 和扩散诱导应变张量 E ^c 是

分别。

代入方程。 (6) 转化为方程。 (8)、格林-拉格朗日应变张量的径向分量和切向分量为

变形的本构关系可由应变能密度确定为

其中 W 是拉格朗日描述中的弹性应变能量密度，P 是第一个 Piola-Kirchhoff 应力。此外，如果材料是线弹性的，W 可以写成格林-拉格朗日应变张量的二次函数

在这里，E h 和 ν 分别是杨氏模量和泊松比，C 是刚度张量，而 det(F ^c )是扩散诱导变形的变形梯度张量的决定因素。

最后，第一个 Piola-Kirchhoff 应力为

结合方程。 (5)、(9)、(10)、(13)，第一Piola-Kirchhoff(P-K)应力张量的对应分量为

且第一P-K应力必须满足无体力时的平衡条件

具有初始和边界条件

质量传输方程

电极中锂的浓度和扩散通量是坐标和时间的函数，称为C (X , t) 和 J (X , t) 在拉格朗日描述中，他们应该满足写成

其中 Div 表示拉格朗日描述中的散度算子。考虑到球对称的特性，扩散只发生在径向，我们使用J (R , t) 表示 J 的径向分量 (X , t)。在球面系统中，方程。 (18) 变成

锂在电极中的扩散由化学势梯度驱动，径向通量J (R , t) 正比于化学势梯度μ , 如 [11]

其中 D 是扩散系数，R g 是气体常数，T 是温度。 μ 定义为总能量密度对浓度的偏差，可以写成

假设系统的能量密度 Π 可以描述为化学能密度和应变能密度之和。因此，总内能密度可写为

代入方程。 (22) 代入式(21)，化学势μ 可以显示为

其中 μ 0(C ) 和 τ (E ^e , C ) 分别是化学势的应力无关和应力依赖部分。和

其中 μ 0 是一个常数，表示标准状态下的化学势，γ 是活度系数，表示原子/分子之间相互作用的影响。对于稀溶液，原子/分子之间的相互作用可以忽略不计；因此，γ =1.

我们专注于化学势的应力依赖部分τ (E ^e , C)，它是应变能密度W的导数 关于锂 C. 的浓度 传统上，Π(X , t) 被认为是亥姆霍兹自由能密度，因此这一步是针对固定变形进行的，写为[11]

下标H 意味着它是由亥姆霍兹自由能密度引起的。化学势为

其中 σ 米 是欧拉描述中的柯西静水应力，可由下式获得

值得注意的是刚度C 假设电极材料的浓度与锂 C 的浓度无关 在方程式中(12).此外，det(F ^e ) ≈ 1 被广泛接受，因此通常被忽略。在本文的其余部分，我们称方程。 (26) 作为化学势的传统表达。另一方面，Π(X , t) 在一些关于相场模型的研究 [12, 13] 中被认为是吉布斯自由能密度，因此我们无法得到 τ 的发达表达式 (E ^e , C), 和

下标 G 意味着它是由吉布斯自由能密度引起的。在这种情况下，μ 变成

我们称方程。 (29) 作为化学势的发达表达。

质量传递方程由方程组成。 (19)、(20)、(26) 和 (29) 与化学势的传统和发达的表达。在本文的其余部分，我们将比较这两种化学势表达式对不同充电方式下扩散诱导应力和锂离子浓度的影响。

在热力学中，亥姆霍兹自由能是一种热力学势，它测量在恒定温度和体积下从封闭热力学系统可获得的有用功。相比之下，吉布斯自由能衡量的是热力学系统在恒定温度和压力下可以做的最大可逆功。在低应力水平的固体中，吉布斯自由能近似等于亥姆霍兹自由能，因为固体的变形通常很小。这种假设适用于大多数固体材料，因为它们的扩散引起的变形很小，但硅除外，因为它在锂化过程中体积膨胀很大。事实上，扩散和变形是同时发生的，因此假设浓度变化时不发生变形是不合适的。即便如此，从方程可以看出。 （25），当变形率足够低时，化学势的传统表达仍然准确。然而，当Si纳米粒子电极快速锂化时，容易造成很大的误差。

电极在其表面以恒定的锂离子浓度进行锂化，即恒电位操作，或在其表面以恒定的通量进行锂化，即恒电流操作。方程的边界条件。 (19) 是

分别。初始条件写为

每次充电操作。在这里，C max 是材料的最大锂浓度，j 0为代表充电电流的常数。

数值实现

获得上述由偏微分方程组成的系统的解析解是非常困难的，如果不是不可能的话。与方程。 (1)–(3) 和 (13)–(18)，我们使用 COMSOL 多物理场软件数值计算了扩散诱导应力和锂浓度的演变。研究了在恒电位和恒电流操作下硅纳米电极的锂化，化学势的不同表达。模拟中使用的Si的材料特性和工作参数列于表1中。为方便起见，图中采用相应的坐标、应力和浓度的无量纲代换。

为研究球形Si电极不同时间化学势不同表达的差异，计算荷电状态（SOC）为

拉格朗日描述中的应力诱导扩散通量描述为

分别代表不同化学势表达式引起的通量。

结果与讨论

图 1 显示了在几个 SOC 下恒电流操作下球形 Si 电极中锂浓度、径向应力和环向应力的空间分布。为了比较，包括化学势的发展和传统表达的数值结果，它们分别用实线和三角形符号表示。对于图 1a 中的每个 SOC，实线几乎与三角形符号重叠。化学势的不同表达对锂浓度的影响可以忽略不计。在图 1b 和图 1c 中，对于 46.7% 和 65.5% 的 SOC，实线高于中心的三角形，而它们在外面几乎重叠，就像其他 SOC 一样。整体而言，恒电流操作下对锂的浓度和应力有轻微影响。图 2 显示了在几个 SOC 的恒电位操作下，球形 Si 电极中锂浓度、径向应力和环向应力的空间分布。值得一提的是，图1和图2中径向和环向应力随着SOC的增加先增加后减小。这是因为硅电极在初始状态或完全锂化状态下是无应力的，因为没有浓度梯度。与图 1a 相比，图 2a 中实线和三角形的差异更大。由于表面上的锂浓度是恒定的C max 在恒电位操作下，充电率高于恒流操作的变形率，变形率也一样。但是，无论充电方式如何，相同SOC下的总变形量几乎相同，只是时间不同。表明化学势的不同表达对锂分布的影响只与变形速率有关，与变形无关，并且随着变形速率的增加而增加。事实上，现有的实验表明，在某些充电模式下，硅电极在锂化过程中变形非常快。正如我们从图 3 [17] 中看到的，Si 负极在 1 分钟内完全变形，相对于锂金属的电位为 2-V。在这种情况下，这两种化学势表达式求解的结果将有显着差异。不幸的是，在这种情况下，电极的应力无法准确测量，因此无法与我们的模型进行定量比较。

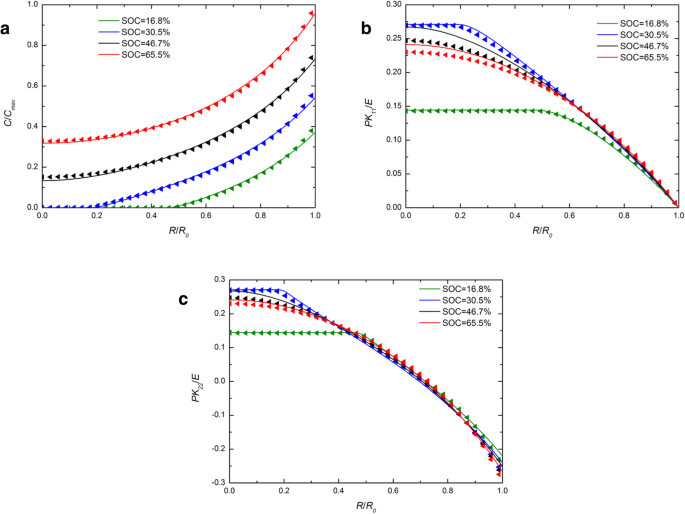
(a 的空间分布 ) 锂的浓度，(b ) 径向应力，和 (c ) 恒电流操作下球形Si电极在不同S​​OC下的环向应力（实线代表化学势传统表达式的结果；三角形线代表化学势发展表达式的结果）

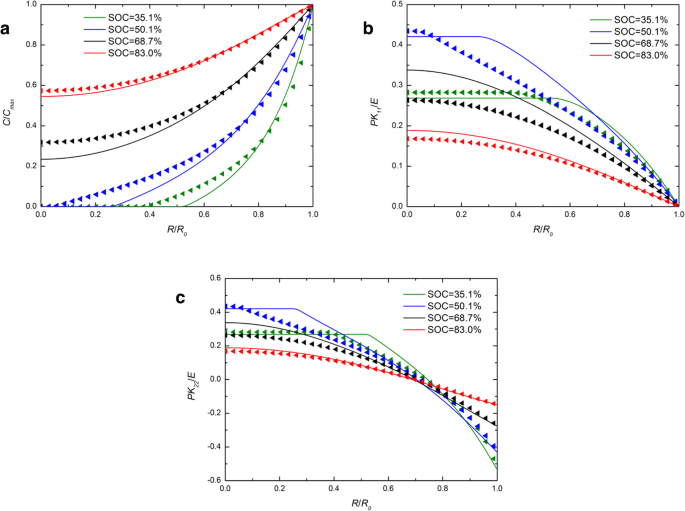
(a 的空间分布 ) 锂的浓度，(b ) 径向应力，和 (c ) 不同SOCs下球形Si纳米粒子电极在恒电位操作下的环向应力（实线代表化学势传统表达式的结果；三角线代表化学势发展表达式的结果）

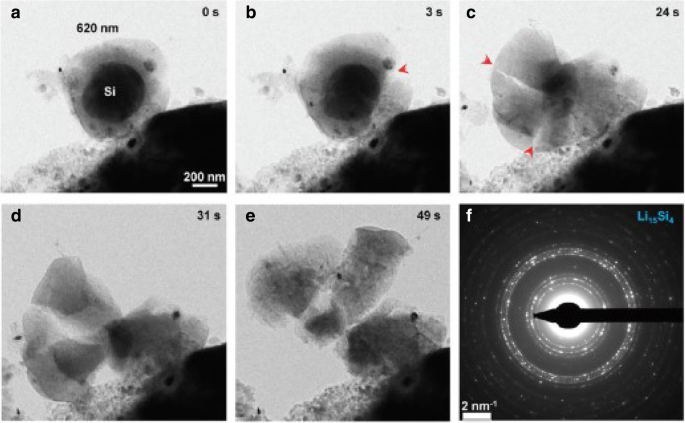
在 1 分钟内化学锂化过程中自立式 620-nm SiNP 的快速变形。 一 –e 裂纹萌生和扩展的时间顺序。 f EDP​​表明形成了多晶Li15Si4作为完全锂化相

图4显示了J的空间分布 H /J G 在不同 j 恒电流操作下不同 SOC 下的球形 Si 电极 .在图4中，实线与三角形几乎重合，说明不同的化学势表达式对J的比值有轻微影响 H 和 J G .很明显，J 的取值范围 H /J G 随着充电电流的增加而增加。这是因为更大的充电电流会导致更高的变形率，从而导致不同化学势表达的更大影响。该比率始终在中心大于 1，在表面小于 1。这表明从表面化学势的发展表达式获得的通量大于传统表达式获得的通量，而在中心则相反。我们注意到图 4 中的所有实线和三角形几乎与一个点相交。此外，无论电极以何种电流充电，与交点对应的比率始终约为1。这表明存在一个临界半径，其中通量受不同化学势表达式的影响较小。我们称其为化学势独立区 (CIR)。显然，CIR总是靠近球形电极的表面，随着充电电流的增加，CIR越靠近表面。

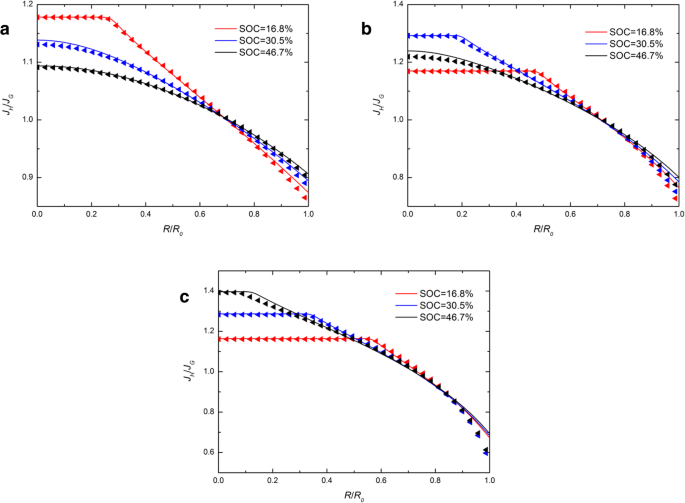
J的空间分布 H /J G 在不同 SOC 下的球形 Si 纳米粒子电极中，在恒电流操作下 (a ) j =0.5j 0, (b ) j =j 0 和 (c ) j =1.5j 0（实线代表化学势传统表达式的结果；三角线代表化学势发展表达式的结果）

通过比较方程中的传统和发达的化学势。 (26) 和方程。 (29) 发现柯西静水应力σm 是这两个表达式之间差异的关键。为了研究 CIR 的成因，图 5 和图 6 给出了不同 SOC 下球形 Si 电极在不同 SOC 下的 σm/E 空间分布和不同化学势表达式。显然，几乎所有曲线都相交在 CIR 的某一点上，Cauchy 静水应力 σm 在这一点上接近于 0，除了在充电开始时 (SOC =6.2%)。这表明 CIR 中的 σm 在大部分充电周期内保持在低水平（接近 0）。可以解释，当静水应力σm 接近0 时，两种化学势表达式几乎等价。这或许可以部分解释CIR 出现的原因，但不足以解释σm 上的曲线特征。需要我们接下来的研究来解决。

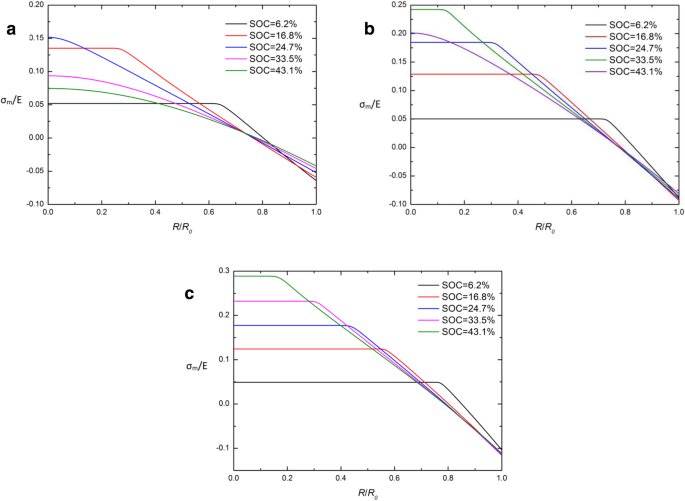
σ的空间分布 恒电流操作下球形Si纳米粒子电极在不同S​​OC下的m/E，化学势和(a ) j =0.5j 0, (b ) j =j 0 和 (c ) j =1.5j 0

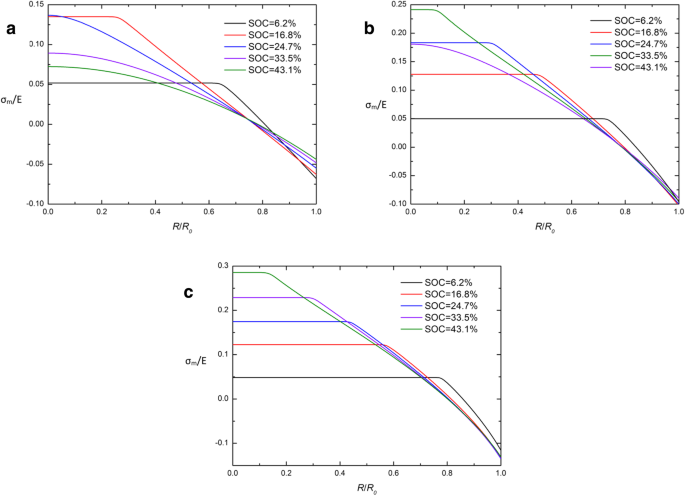
σ的空间分布 恒电流操作下球形Si纳米粒子电极在不同S​​OC下的m/E，化学势的发展表达式（a ) j =0.5j 0, (b ) j =j 0 和 (c ) j =1.5j 0s

结论

在这项工作中，提出了化学势的发展表达式，没有低变形率假设，区别于目前广泛使用的发展表达式。讨论了在恒电位和恒电流操作下化学势在Si纳米粒子电极应力和浓度分布上的传统表达和发展表达的差异。

结果表明，在恒电流操作下化学势的不同表达所引起的影响可以忽略不计，而在恒电位操作下却是显着的。发现该影响仅与变形率有关，与变形无关，并且随着变形率的增加而变大。考虑到传统化学势表达式中的低变形率假设，认为开发的化学势表达式得到的结果更可靠。在纳米粒子电极表面附近发现了化学势无关区域 (CIR)，在大多数锂化过程中，由传统和发展的化学势引起的通量几乎相同。此外，随着充电电流的增加，CIR 更靠近表面。类似的现象也出现在柯西静水应力曲线中。无论使用哪种化学势表达式，Cauchy 静水应力 σm 都保持恒定并在 CIR 中最多保持在较低水平（接近 0）。此类结果尚未见文献报道。

数据和材料的可用性

本研究中分析的数据集可在合理要求下从通讯作者处获得。

缩写

CIR：

由这两种化学势表达引起的扩散通量几乎相同的区域