单晶 6H-SiC 滑移变形和纳米机械加工性的原子级表征

介绍

碳化硅作为第三代宽带隙半导体材料，具有击穿场强高、辐射耐受性高、载流子饱和速度快、导热快、介电常数小、化学性质稳定等特点，在各个领域有着广泛的应用高温、高频、大功率、抗辐射、短波长光电器件与光电集成的研究[1]。

使用最广泛的碳化硅晶体是 3C、4H 和 6H。磨削/研磨/抛光等加工方法仍然是单晶碳化硅加工过程中的主要方法。然而，金刚石和碳化硅的硬度比接近2:1（加工深度<50 nm）），远低于加工工艺推荐值5:1[2]。刀具的严重磨损和次表面损伤直接影响晶片的质量。为了解决这些问题，已经进行了大量工作来了解纳米级 SiC 的去除行为。对 3C-SiC 的去除机理和加工因素的影响进行了深入研究，如切削过程中的塑性变形机制 [3,4,5,6,7]、刀具磨损 [8]、摩擦行为 [9] ]、3C-SiC的各向异性[10]及切削温度的影响[11]。

6H-SiC 具有更复杂的 ABCACB 堆叠结构。虽然研究了 6H-SiC 在 SPDT（单点金刚石车削）加工中的去除机理（如刀具前角对材料去除过程的影响 [12] 和脆-韧转变 [13]），但该研究显然是小于3C-SiC。 6H-SiC（3 eV）的带隙明显高于3C-SiC（2.3 eV）。目前，6H-SiC棒生长工艺的技术水平远高于3C-SiC。 6H-SiC 在工业应用中的应用远比 3C-SiC 多。相应的器件已在高频、大功率、高温领域得到应用，如肖特基整流器、闸流管、功率MOSFET（Metal-Oxide-Semiconductor Field-Effect Transistor）。为了提高6H-SiC的加工表面/亚表面质量，目前最有效和有效的手段是寻找更适合6H加工的晶面（加工面）/晶向（加工方向）的合适组合-碳化硅。

划痕实验和模拟是探索去除行为的一些最常见和最有效的方法 [14, 15]。划痕过程中材料去除机理的研究对实际磨料加工过程具有重要的指导意义。分子动力学方法可以提供纳米尺度的损伤形成和去除过程。因此，利用分子动力学划痕模拟分析了6H-SiC在晶体学诱导各向异性影响下的去除行为。

方法论

本文中的切割模拟是使用大规模原子/分子大规模并行模拟器 (LAMMPS) [16] 完成的。本研究中使用 OIVTO [17] 和金刚石结构识别方法 [18] 进行模型可视化和缺陷识别。工件和工具建模的实现依赖于 LAMMPS，而无需其他软件的帮助。如图 1a-c 所示，工件和工具都被设置为可变形体，并且在模拟过程中研究了磨损行为。刀具和工件模型分为三个部分：边界原子层、恒温原子层和牛顿原子区。为了使工件保持在初始位置，工件底部和右端的边界层原子被固定。恒温层和牛顿层中的原子遵循牛顿第二定律。沿 y 应用周期性边界 方向。在划痕模拟之前，模型通过采用 Berendsen 恒温器方法的 NVE 集成进行松弛。在划痕模拟之前应用 50 ps 弛豫期以获得稳定的能量状态。磨料形状为球冠三角锥，棱角为90°。如图 2 所示，选择 6H-SiC 的共同晶面（a 面（基面）、m 面（棱柱面）和 c 面）作为加工表面。考虑到结构的对称性，选择以下平面/方向组合作为加工面/加工方向：\( (0001)/\left[2\overline{1}\overline{1}0\right] \)， \( (0001)/\left[10\overline{1}0\right] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{ 1}0\right] \), \( \left(01\overline{1}0\right)/\left[0001\right] \), \( \left(11\overline{2}0\right) /\left[1\overline{1}00\right] \) 和 \( \left(11\overline{2}0\right)/\left[0001\right] \)。模拟的加工参数如表1所示。在划痕模拟之前，将磨料放置在工件的左侧，磨料尖端在工件上表面下方50 Å处。磨料与工件之间的最近距离为 30 Å，远离相互作用电位的截止范围。磨料从工件的自由端沿x的正方向运动 -axis 并完成划痕过程。

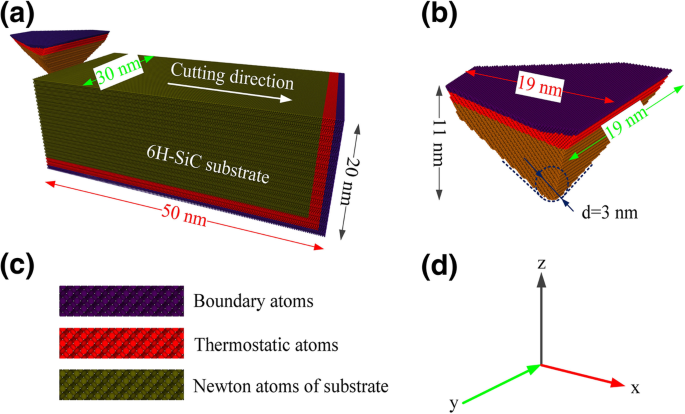
一 纳米划痕模拟的 MD 模型。 b 工具的形态。 c 模型的结构。 d 轴方向

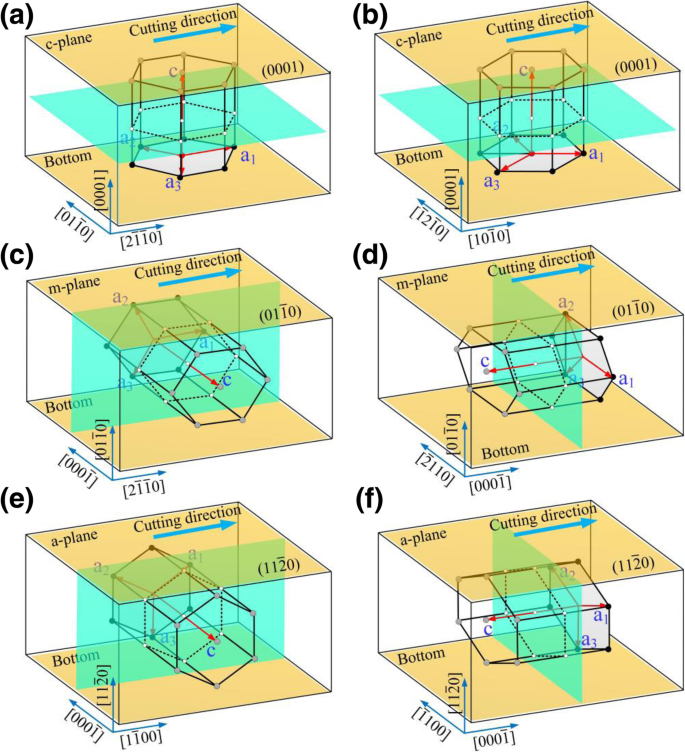
划痕过程示意图，其中a –f 分别是对应的工艺模式\( (0001)/\left[2\overline{1}\overline{1}0\right] \), \( (0001)/\left[10\overline{1}0\right ] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \), \( \left(01\overline{ 1}0\right)/\left[0001\right]\)、\(\left(11\overline{2}0\right)/\left[1\overline{1}00\right]\)，和\( \left(11\overline{2}0\right)/\left[0001\right] \) 分别

原子势函数对分子动力学模拟的准确性和可靠性起着至关重要的作用。根据之前对单晶 SiC 的机械性能和去除机制的测试和模拟，Erhart 和 Albe [19] 提出的分析键序势 (ABOP) 函数更适合于硅和碳的相互作用。势函数中使用的参数如表 2 [19] 所示。代替 Tersoff 势能函数 [6]，ABOP 势能函数用于定义加工过程中刀具和工件内部和之间的 Si-Si、CC 和 Si-C 相互作用 [2, 7, 8, 10, 11]。

结果与讨论

纳米机械加工性分析

如图所示。由图 3 和图 4 可见，6H-SiC 的各向异性对纳米机械加工性（加工深度、去除方式、去除量和次表面损伤深度（SSD）等）有显着影响。根据加工面/加工方向与基面/c的关系 轴（见图3），材料加工方式可分为三类：（i）选择基面作为加工面，（ii）基面垂直于加工面和c -axis 垂直于加工方向，并且 (iii) c -轴平行于加工方向。

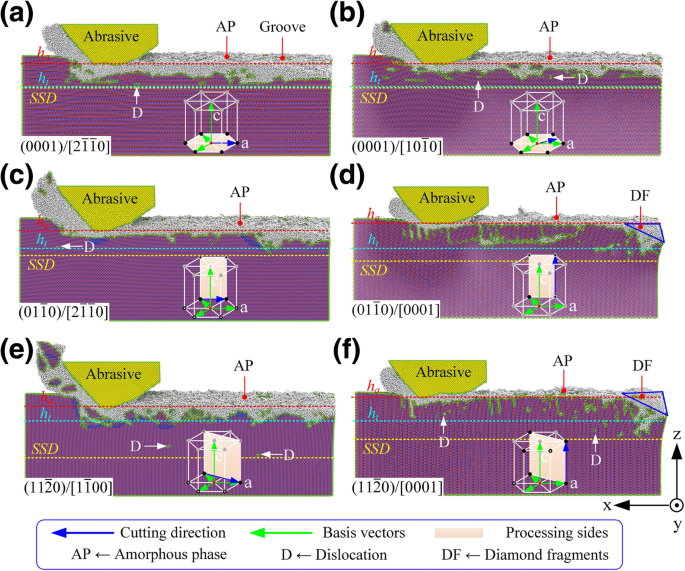
不同晶面/取向条件下加工表面形貌，其中a –f 分别是对应的工艺模式\( (0001)/\left[2\overline{1}\overline{1}0\right] \), \( (0001)/\left[10\overline{1}0\right ] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \), \( \left(01\overline{ 1}0\right)/\left[0001\right]\)、\(\left(11\overline{2}0\right)/\left[1\overline{1}00\right]\)，和\( \left(11\overline{2}0\right)/\left[0001\right] \) 分别

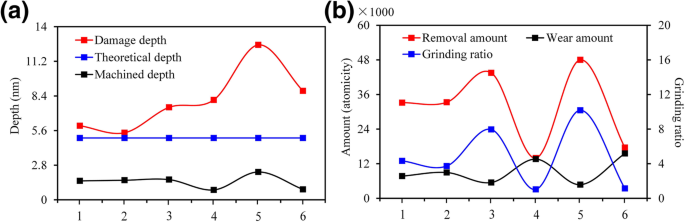
不同晶面/取向条件下的纳米机械加工性，a 各向异性对加工深度和损伤深度的影响，b 各向异性对去除量、磨损量和磨削比的影响。 1、2、3、4、5、6分别是对应的处理方法\((0001)/\left[2\overline{1}\overline{1}0\right]\),\((0001)/ \left[10\overline{1}0\right] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \), \( \left(01\overline{1}0\right)/\left[0001\right] \), \( \left(11\overline{2}0\right)/\left[1\ overline{1}00\right] \) 和 \( \left(11\overline{2}0\right)/\left[0001\right] \) 分别。损伤层深度是指划伤引起晶体内部缺陷的最大深度。理论深度是指加工前的预设深度。加工深度是指划伤后的残留深度。去除量是指去除工件材料的原子数。磨损量是指划痕前后磨粒原子数的差异

(i) 如图 3a、b 所示，当加工模式选择为 \( (0001)/\left[2\overline{1}\overline{1}0 \right] \) 和 \( (0001)/\left[10\overline{1}0\right] \)。然而，当加工模式选择为\((0001)/\left[10\overline{1}0\right]\)时，6H-SiC的去除过程更倾向于脆性模式。 (ii) 如图 3c、e 所示，当处理模式选择为 \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0 \right] \) 和 \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \)，加工深度和材料去除量明显高于那些在其他处理方法中。如图4所示，在相同的理论加工深度(h t =5.0 nm)，加工模式\( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \)下的材料去除率是3.4倍在处理模式\( \left(01\overline{1}0\right)/\left[0001\right] \)。材料加工比（材料去除量/刀具磨损）为10.1，但该加工参数下的SSD也远高于其他加工条件下的SSD，达到\((0001)/\left[10\overline{的2.3倍) 1}0\右]\)。在加工表面和切屑上有大量的纳米微晶。在这种情况下发生了大量的脆性破坏。加工方式\( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \)只适用于加工效率要求高但对加工不敏感的纳米槽加工。次表面损坏。 \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \) 的材料去除率与\( \left (11\overline{2}0\right)/\left[1\overline{1}00\right]\) 但 SSD 仅为后者的 50%。此外，加工表面的非晶层厚度远低于 \( (0001)/\left[2\overline{1}\overline{1}0\right] \) 和 \( (0001) /\left[10\overline{1}0\right] \)。次表面相分布均匀，整个凹槽的力学性能优于其他加工方法。因此，加工方式\( \left(01\overline{1}0\right)/\left[0001\right] \)是在6H-SiC表面高效加工微纳槽的最佳选择、高精度、低SSD。 (iii) 如图所示。 3d, f, 当加工方向平行于c -轴，尖端在初始加工阶段严重磨损。虽然加工深度和材料去除率远低于其他加工方法，材料加工比仅为1.0左右，但SSD为\( \left(01\overline{1}0\right)/\left[ 0001\right] \) 和\( \left(11\overline{2}0\right)/\left[0001\right] \) 处理模式比\( \left(01\overline{1} 0\right)/\left[2\overline{1}\overline{1}0\right]\)因此，不建议使用 \( \left(01\overline{1}0\right)/\left[0001\right] \) 和 \( \left(11\overline{2}0\right)/ \left[0001\right] \) 在 6H-SiC 表面加工微纳米凹槽。然而，这些模式表现出优异的耐磨性；因此，它们适用于单晶碳化硅刀具的前刀面，在黑色金属超精密加工领域具有广阔的前景。

唇部运动和次表面损伤分布分析

基于三角金字塔提示的Scratch过程中Schmid因子分布

常见的六方晶系滑移系（见图4）主要有基底滑移、棱柱滑移和锥体滑移。滑移阻力与广义堆垛层错能 (GSF) 和 dE 有关 GSF/dx 与 (x /b ) 的滑动系统。滑移将发生在最密集的平面上，并沿着最短的方向 [10]。基础滑动中的优先滑动系统是基础滑动(shuffle set)/<\( 1\overline{1}00 \)>和基础滑动(shuffle set)/<\( 11\overline{2}0 \)> [20]。由于前者缺乏中间能量最小值，后者在模拟和实验中优先[20]。因此，在这项工作中考虑的滑动运动如下：基础滑动（shuffle set）/<\( 11\overline{2}0 \)> 和棱柱 滑动和 滑动。图5.

<图片>

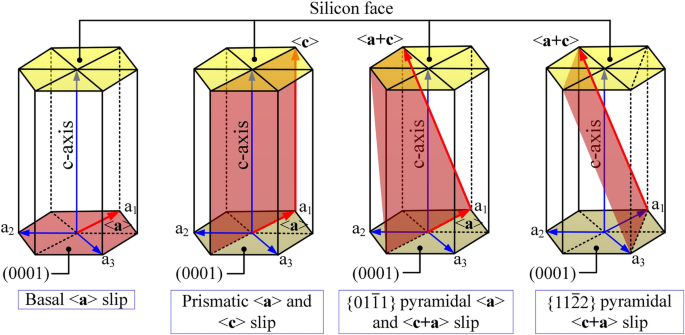
六方系滑移系

滑翔平面上的剪应力分量τ ss 可以通过以下关系计算：

$$ {\tau}_{\mathrm{ss}}={\sigma}_{\mathrm{cont}}\mathit{\cos}<\overset{\rightharpoonup }{f},\overset{\rightharpoonup } {n_g}>\cos <\overset{\rightharpoonup }{f},\overset{\rightharpoonup }{t_g}>={\sigma}_{\mathrm{cont}}\bullet m $$ (1)

其中 σ cont 是接触应力，\( \overset{\rightharpoonup }{f} \) 是加载方向，\( \overset{\rightharpoonup }{n_g} \) 和\( \overset{\rightharpoonup }{t_g} \)是全局笛卡尔坐标系中的滑移平面法线和滑移方向，m 是施密德因子。全局坐标系固定，局部坐标系随晶体方向旋转。 x 局部坐标系的 -axis 平行于基本向量 \( \overset{\rightharpoonup }{a_1} \) 而 z -axis 平行于基本向量 \( \overset{\rightharpoonup }{c} \).

在刮削过程中，三棱锥尖端的主要接触面是前刀面，但当刀具磨损严重时，主接触面转变为前刀面和尖端的复合物。对应的加载方向 \( \overset{\rightharpoonup }{f} \) 表示为

$$ \left\{\begin{array}{c}\overset{\rightharpoonup }{f_1}=\left({f}_{1x},{f}_{1y},{f}_{1z} \right)\kern8em \mathrm{rake}\ \mathrm{face}\ \\ {}\overset{\rightharpoonup }{f_2}=\left({f}_{2x},{f}_{2y}, {f}_{2z}\right)\kern9.75em \mathrm{tip}\ \mathrm{top}\end{array}\right。 $$ (2)

其中 \( \overset{\rightharpoonup }{f_1}=\left(1,0,-\sqrt{2}\right) \), \( \overset{\rightharpoonup }{f_2}=\left(0,0 ,-1\right) \) 在全局坐标系中。

作为六方晶系，6H-SiC的滑移系可以表示为{h k i l }/ <u v t w>.局部笛卡尔坐标系中的滑移平面法线\( \overset{\rightharpoonup }{n_c} \) 和滑移方向\( \overset{\rightharpoonup }{t_c} \) 表示为

$$ \overset{\rightharpoonup }{n_c}=\left(\frac{3}{2}h,\frac{\sqrt{3}}{2}\left(h+2k\right),\frac{ 3 la}{2c}\right) $$ (3) $$ \overset{\rightharpoonup }{t_c}=\left(u-\frac{1}{2}\left(v+t\right),\压裂{\sqrt{3}}{2}\left(vt\right),\frac{c}{a}w\right) $$ (4)

全局笛卡尔坐标系中的滑移平面法线\( \overset{\rightharpoonup }{n_g} \) 和滑移方向\( \overset{\rightharpoonup }{t_g} \) 表示为

$$ \overset{\rightharpoonup }{n_g}=T\bullet \overset{\rightharpoonup }{n_c} $$ (4) $$ \overset{\rightharpoonup }{t_g}=T\overset{\rightharpoonup }{\子弹{t}_c} $$ (5)

其中从全局坐标系到局部坐标系的旋转矩阵形式及对应的旋转角度见表3

根据公式(1)-(5)，加载方向为\( \overset{\rightharpoonup }{f_1} \) 和\( \overset{\rightharpoonup }{f_2} \) 时对应滑移系统的Schmid因子)如表4所示。 (i) 6H-SiC的c/a值达到4.901，远大于1.633。因此，基底滑移所需的临界剪应力低于棱柱滑移系统所需的临界剪应力。当加工面为基面时，基面滑移系系数高于其他滑移系。因此，当处理模式选择为 \( (0001)/\left[2\overline{1}\overline{1}0\right] \) 和 \( (0001)/\left[10\overline{1 }0\right] \)，基础 滑动运动首先发生。 (ii) 当处理模式选择为 \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \) 和 \( \ left(11\overline{2}0\right)/\left[1\overline{1}00\right] \)，只考虑加载方向 \( \overset{\rightharpoonup }{f_1} \) 和 \( \overset{\rightharpoonup }{f_2} \)，理论上不可能发生基底滑移，而棱柱滑移运动优先。 (iii) 当处理模式选择为 \( \left(01\overline{1}0\right)/\left[0001\right] \) 和 \( \left(11\overline{2}0\right )/\left[0001\right] \)，如图 4 所示，尖端在初始加工阶段磨损严重，\( \overset{\rightharpoonup }{f_2} \) 在抓挠的过程。因此，滑移运动会发生在与YOZ平面在全局坐标系中对称分布的棱柱滑移系中。

表面/次表面损伤分布

如图6a，b当\((0001)/\left[2\overline{1}\overline{1}0\right]\)和\((0001)/\left[01\overline{1 }0\right] \) 时，滑移运动主要发生在滑移系 \( (0001)/<1\overline{2}10> \) 上，这是由于工具向前推动。相应的滑动运动方式与施密特系数的计算结果一致。亚表面区域存在纳米晶粒和晶格偏转，这些损伤形成了一些不规则的晶格畸变区。非晶相覆盖整个加工表面，位错深度接近晶格畸变层深度。

<图片>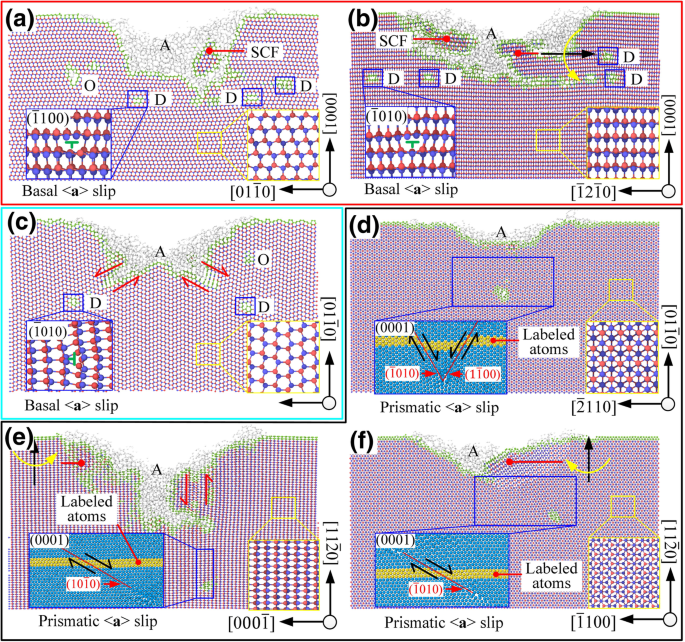

加工区域的横截面，D 是错位，A 是非晶相，SCF 是单晶形式，O 是其他类型的缺陷，其中 a –f 分别是对应的工艺模式\( (0001)/\left[2\overline{1}\overline{1}0\right] \), \( (0001)/\left[10\overline{1}0\right ] \), \( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \), \( \left(01\overline{ 1}0\right)/\left[0001\right]\)、\(\left(11\overline{2}0\right)/\left[1\overline{1}00\right]\)，和\( \left(11\overline{2}0\right)/\left[0001\right] \) 分别。

当\（\ left（01 \ ovline {1} 0 \右）/左[2 \ ovline {1} \ overline {1} 0 \右] \）被选中，作为基础<的施密特系数一个>滑动等于0，基础<a> 理论上不应发生滑移。但是加载方向\( \overset{\rightharpoonup }{f_1} \) 和滑动方向\( \left[11\overline{2}0\right] \) 之间的夹角仅为5.3°。由于接触区和非接触区之间的相对运动（见图6c），在剪切作用下，基底<a> 在\( \left(01\overline{1}0\right)/\left[2\overline{1}\overline{1}0\right] \)的处理模式下，在棱柱滑移之前触发滑移并且发生在 V 型槽的两侧。在\( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \)的处理方式下，加载方向\( \overset{\rightharpoonup }{f_1} \) 和滑动方向 \( \left[1\overline{2}10\right] \) 和 \( \left[\overline{1}\overline{1}20\right] \) 是分别为 24.7° 和 35.3°。剪切作用不会引起基面的滑动。相应的滑移模式与施密特系数的计算结果一致。 As shown in Fig. 6e, when \( \left(11\overline{2}0\right)/\left[1\overline{1}00\right] \) was selected, the slip system \( \left[ 1\overline{2}10\right]/\left(\overline{1}010\right) \) 在 \( \overset{\rightharpoonup }{f_1} \) 和 \) 的共同作用下具有很高的施密特系数( \overset{\rightharpoonup }{f_2} \)，这将不可避免地导致地下损伤层的深度很大。晶格畸变和非晶相也存在，但与基面加工不同，位错深度明显大于晶格畸变的位错深度。 sp ³ →sp ² 过渡行为发生在次表层区域。

当加工方向平行于c 轴，由于尖端磨损严重，向下挤压引起的棱柱滑移是稳定刮擦阶段的主要滑移运动方式。相应的滑移模式与施密特系数的计算结果一致。当\（\左（01 \ overline {1} 0 \右）/左键[0001 \右] \）被选中，使用加载方向\（\ versteT {\ Rightharpoonupup} {f_2} \），滑动系统\( \left[1\overline{2}10\right]/\left(\overline{1}010\right) \) 和 \( \left[\overline{1}\overline{1}20\right] /\left(1\overline{1}00\right)\) 具有相同的施密特系数，在两个夹角为 60°的滑移面上发生交叉滑移，然后发生钉扎效应阻碍滑移运动.因此，最大次表面损伤深度SSD max 将小于或等于 h t tan θ /2 cot α /2，其中θ =101° 是纳米槽的理论角度，α =60° 是滑移面 \( \left(\overline{1}010\right) \) 和 \( \left(1\overline{1} 00\右)\)当\（\左（11 \ overline {2} 0 \右）/ \左[0001 \右] \）被选中时，spl systems \（\ lefth [\ overline {2} 110 \ lex] / \ left 0\overline{1}10\right) \) 和 \( \left[1\overline{2}10\right]/\left(\overline{1}010\right) \) 也有相同的施密特系数，但滑移运动受尖端不规则磨损的影响，仅发生滑移系统\( \left[1\overline{2}10\right]/\left(\overline{1}010\right) \)。

总之，如图 7 所示，在不同加工条件下，次表面区域的损伤主要是位错、晶格畸变（扭转/相对滑动）和非晶相。 6H-SiC的变形主要是由滑动运动、材料的非结晶和不规则的晶格畸变引起的。主要的滑移变形方式为基底滑移和棱柱滑移，与加工面/方向密切相关。

<图片>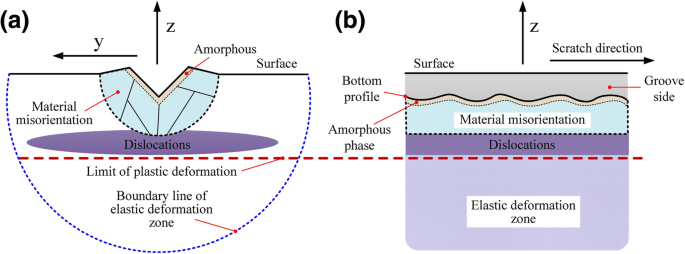

处理过的表面/次表面损伤形式分布。 一 xy 横截面。 b xz 横截面