Coin Paradox 自旋-轨道相互作用增强磁光效应及其在片上集成光隔离器中的应用

介绍

基于非互易传输的光隔离器是光通信和光信息中的关键光子元件。要实现集成度更高的光隔离器，方法很多，如利用磁光效应[1,2,3,4,5]，拓扑学[6]，非线性效应[7,8,9,10,11, 12] 和奇偶时间对称性破缺 [13,14,15]，已经被开发出来。其中，磁光效应仍然是一个热点。然而，到目前为止，所创建的设备通常是大规模的 [2, 16]，因为在这些情况下磁光效应大多很弱。

表面等离子体激元（SPP）可以突破衍射极限[17, 18]，在集成光学领域具有极好的潜力[19,20,21]，尤其是在SPP损耗高的问题得到改善后[22]。 SPP 具有横向自旋角动量 (TSAM) [23,24,25]，可以诱导磁光效应以实现类似于光的纵向自旋角动量 (LSAM) 的非互易传输 [26,27,28 ]。然而，由于磁光效应较弱，基于SPP横向磁光效应的隔离器很难小型化。导致SPP横向磁光效应弱的主要原因有两个：一是磁光材料的磁光系数小，二是SPP的横向自旋不是圆形，而是椭圆形[26]。目前，已经制造出多种具有大磁光系数的磁光材料并应用于光隔离器[4,29,30,31,32]。这为创建具有等离子体结构的小型化光学隔离器带来了希望。但是，另一方面，SPP的椭圆横向自旋仍然是横向磁光效应应用的瓶颈。仍有待发现增强横向磁光效应的新方法。

自旋和轨道角动量（SAM 和 OAM）是两个不同的光分量。它们可以有效地相互作用，即通过自旋轨道相互作用 (SOI)。已经发现了许多基于光的 SOI 的重要和有价值的光学效应，包括自旋霍尔效应、量子自旋霍尔效应、拓扑学等。 硬币悖论是一种迷人的自然现象，它表现出独特的 SOI，即圆周轨道导致旋转自旋变化。因此，硬币悖论SOI可能是调节SPP横向磁光效应的一种新的物理机制。

这项工作报告了一种简单的片上集成光隔离器的设计，该隔离器由金属-绝缘体-金属 (MIM) 波导和填充有磁光材料的圆盘腔组成。在这种光隔离器结构中，通过硬币悖论 SOI 证实了横向磁光效应的有效增强。受益于光隔离器结构中增强的横向磁光效应，当磁光参数\(\varepsilon_{xy}\ge 0.04\)时，透射光谱中的前向和后向谐振谷彼此完全分离。获得了一种高性能的片上集成光隔离器，其最大隔离比 (IR) 大于 60 dB，相应的插入损耗 (IL) 约为 2 dB。由于光隔离器结构中硬币悖论SOI的独特性质，对于较小的方位模数n，横向磁光效应的改善更为显着。横向磁光效应在很宽的波长范围内保持强烈。此外，在较小的圆盘腔内出现较大的横向磁光效应，可以有效地克服较小腔引起的谐振谷的加宽。本文开发的强横向磁光效应结构在片上高集成磁光器件、光隔离器、磁光开关、磁传感器等方面具有巨大的应用潜力。

方法

图 1 显示了由 MIM 波导和盘腔组成的拟议光隔离器结构的示意图。半径 (R ) 圆盘腔的宽度设置为 540 nm，MIM 波导的宽度 d 设置为 50 nm，圆盘腔和 MIM 波导之间的间隙 g 设置为 16.6 nm。金属为银，其频率依赖的复相对介电常数由 Drude 模型表征：

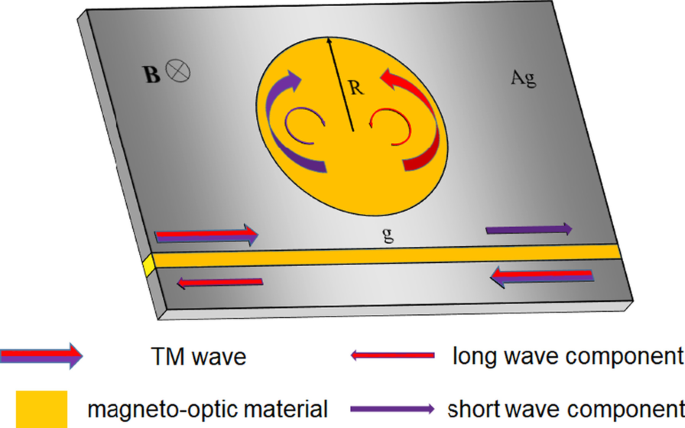
由 MIM 波导和圆盘腔组成的光隔离器结构示意图。 MIM波导和圆盘腔填充磁光材料并保持在静磁场下

这里，\(\varepsilon_{\infty }\) 是无限频率下的介电常数，γ 是电子碰撞频率，\(\omega_{p}\) 是体等离子体频率，ω 是入射光的角频率。放入方程的参数。 (1) 分别是 \(\varepsilon_{\infty }\) =3.7, \(\omega_{p}\) =9.1 eV, γ =0.018 eV [33]。为了激发SPP，输入光被设置为横向磁（TM）平面波。

圆盘腔和 MIM 波导填充有磁光材料，并施加横向静磁场。静磁场对磁光材料的影响主要体现在材料的介电张量上。对于各向异性磁光材料，静磁场B 可以沿 z 方向应用，其中介电张量可以表示为：

磁光材料设置为掺铋钇铁石榴石（Bi：YIG）。石榴石属于立方晶体结构，是各向同性的，所以其介电张量的对角元素是相同的，即\(\varepsilon_{xx} =\varepsilon_{yy} =\varepsilon_{zz} =\varepsilon_{0} =n^{2}\)。对角元素的介电常数 \(\varepsilon_{0}\) 设置为 4.84，这是 YIG 在 1.5 μm 波长附近的典型折射率 [34]。最近，实验证明\(\varepsilon_{xy}\)可以大于0.3[35]，理论预测的[36]\(\varepsilon_{xy}\)比实验得到的要大很多。在这项工作中，\(\varepsilon_{xy}\) 的值设置为 0 到 0.3。该器件可以通过金属辅助化学蚀刻 [37, 38] 和电子束光刻 (EBL) 制备。

商业软件 COMSOL Multiphysics 用于基于有限元方法 (FEM) 的模型构建和仿真计算。为了研究方便，整个结构是二维的。传递的指向向量 S 在入口和出口端积分得到入口能量 \(P_{\text{in}}\) 和出口能量 \(P_{{{\text{out}}}}\), \(P_{ {{\text{in}}}} =\int {{\mathbf{S}}_{1} \bullet {\text{d}}{\varvec{s}}_{1} }\), \ (P_{{{\text{out}}}} =\int {{\mathbf{S}}_{2} \bullet {\text{d}}{\varvec{s}}_{2} }\ ) 和透射率 \(T =10{*}\lg \left( {P_{{{\text{out}}}} /P_{{{\text{in}}}} } \right)\) dB . IL 是前向隔离波长处的后向透射率，使用模拟中获得的透射率数据计算得出。光输入从 MIM 波导的左侧给出，其从右侧的输出在本文中标记为“前向”。相反，从MIM波导右侧输入的光导致从左侧输出，称为“向后”。

结果与讨论

如图 1 所示，圆盘腔支撑着一个迷人的硬币悖论 SOI。例如，对于模式 TM(0,n )，SPP 的横向自旋和轨道自转方向相同。 SPP绕圆盘腔运动一圈，电场矢量旋转n + 1 转。圆形轨道会导致额外的转弯。这种效应类似于硬币悖论并形成独特的 SOI。硬币悖论 SOI 对于较小的 n 更为重要。仿真结果证实硬币悖论SOI可以有效增强横向磁光效应。

图 2 显示了不同 \(\varepsilon_{xy}\) 的光隔离器结构的透射光谱。对于\(\varepsilon_{xy} =0\) 的情况，前向和后向透射光谱重叠，透射光谱显示为黑色实线。红色实线表示\(\varepsilon_{xy} =0.3\) 向前情况的透射光谱，红色虚线表示\(\varepsilon_{xy} =0.3\) 向后情况。如图 2 所示，每个传输光谱中有四个突出的传输谷。对于 \(\varepsilon_{xy} =0\)，四个传输谷分别位于 1936.0 nm、1550.2 nm、1460.0 nm 和 1302.5 nm。对于二维有限元建模，圆盘腔的共振由两个整数 (mi, ni) 表征，这些整数计算径向和方位角波腹。根据插图中磁场的 z 分量的强度分布，谐振模式引起的四个传输谷是：TM0,3、TM0,4、TM1,1 和 TM0,5。在本文中，我们主要关注SPP的横向磁光效应，因此对谐振模式：TM0,3, TM0,4和TM0,5进行了详细研究。

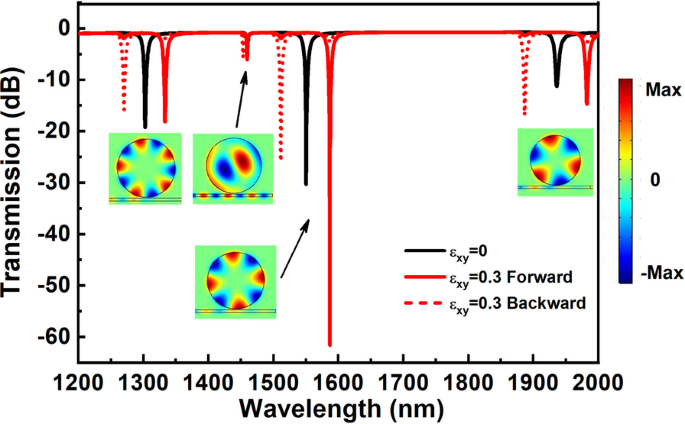
不同 \(\varepsilon_{xy}\) 的光隔离器结构的总透射光谱。黑色实线显示 \(\varepsilon_{xy} =0\) 的透射光谱，\(\varepsilon_{xy} =0.3\) 的红色实线和 \(\varepsilon_{xy} =0.3\) 向后。透射谱下方的插图是磁场z分量的强度分布，对应于\(\varepsilon_{xy} =0\)

首先研究了谐振模TM0,4光隔离器结构的隔离性能。图 3a、b 显示了具有不同 \(\varepsilon_{xy}\) 的谐振模式 TM0,4 的光隔离器结构的透射光谱。在没有任何磁场的情况下，传输谷位于大约 1550.2 nm。在施加磁场时，当 SPP 向前行进时，传输的谷有一个红移，当 SPP 向后行进时，几乎对称地发生蓝移。因此，观察到前向和后向共振谷的分裂。随着磁光参数\(\varepsilon_{xy}\)的增加，波长发生偏移，分裂增加。图 3c 显示了随磁光参数 \(\varepsilon_{xy}\) 变化的前向和后向谐振谷的分裂曲线。如图 3c 所示，分裂实际上与磁光参数 \(\varepsilon_{xy}\) 正相关。图 3d 显示了不同 \(\varepsilon_{xy}\) 的谐振模式 TM0,4 的光隔离器结构的 IR 和 IL。随着\(\varepsilon_{xy}\) 值的增加，前向和后向IL 均减小。此外，当 \(\varepsilon_{xy} \ge 0.05\) 时，IL 小至约 2 dB 并保持稳定。这意味着前向和后向共振谷彼此完全分开。随着 \(\varepsilon_{xy}\) 的增加，前向和后向 IR 表现出不同的变化曲线。如图 3d 所示，我们得到的最大 IR 大于 60 dB，相应的 IL 约为 2 dB。 IR 由传输谷的深度决定。这取决于 MIM 波导和圆盘腔之间的耦合距离。因此，可以通过改变 MIM 波导和圆盘腔之间的间隙来微调 IR，g .相关结果表明，本文提出的光隔离器结构中存在较大的磁光效应，从而获得了高性能的片上集成光隔离器。

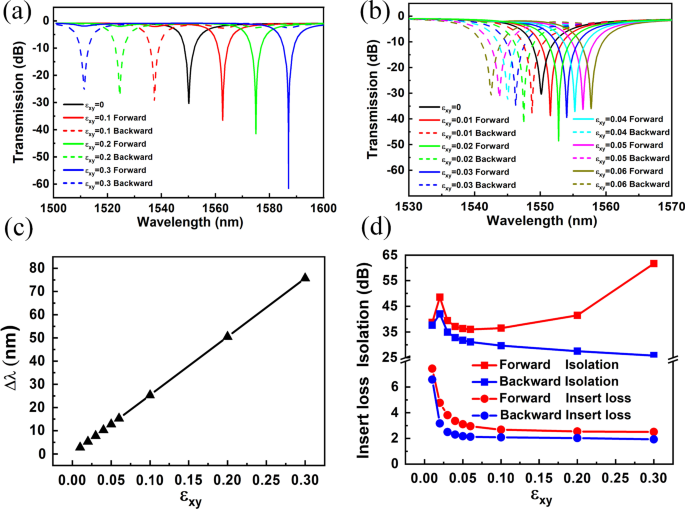
TM0,4 模式下的透射光谱、波长分裂、IR 和 IL。 一 , b 来自不同传播方向的光耦合到具有不同\(\varepsilon_{xy}\) 的圆盘腔的透射光谱。 c , d 作为 \(\varepsilon_{xy}\)

对于较小的方位模数n，硬币悖论SOI对横向磁光效应的增强将更加显着。仿真结果可用于证明该定律。如图 2 所示，对于 TM0,5、TM0,4 和 TM0,3 的情况，分裂 \(\Delta \lambda\) 随方位模数 n 的减小而增加。为了准确比较不同模式的横向磁光效应的强度，不同模式的 \(\Delta \lambda /\lambda\) 比随 \(\varepsilon_{xy}\) 变化的线图绘制在图. 4. 如图 4 所示，对于三种不同的模式，\(\Delta \lambda /\lambda\) 比率只是略有变化。此外，如插图所示，TM0,5 和 TM0,4 的 \(\Delta \lambda /\lambda\) 比率几乎相同，而 TM0,3 的比率最大。这些模拟结果与参考文献中报道的理论相反。 [26]。对于 TM0,5, TM0,4 和 TM0,3 的情况，共振波长随着方位角模数 n 的减小而增加，如图 2 所示。随着波长的增加，金属的绝对值介电常数\(\varepsilon_{M}\) 迅速增加，导致\(\beta_{SPP}\) 的减小。根据参考文献中的理论。 [26]，横向磁光效应预计会减弱，\(\Delta\lambda\)比值更小。因此，目前的模拟结果与参考文献中的理论相反。 [26]。硬币悖论 SOI 对横向磁光效应的增强可以解决模拟结果与参考文献中的理论之间的这一矛盾。 [26]。如上所述，硬币悖论 SOI 对于较小的方位角模式数 n 更为重要。因此，硬币悖论 SOI 对横向磁光效应的增强可以抵消甚至超过由波长增加引发的减弱。此外，还可以得出另一个结论：本文中提到的异常大的横向磁光效应是由硬币悖论SOI引起的，并且在大波长范围内仍然很强。

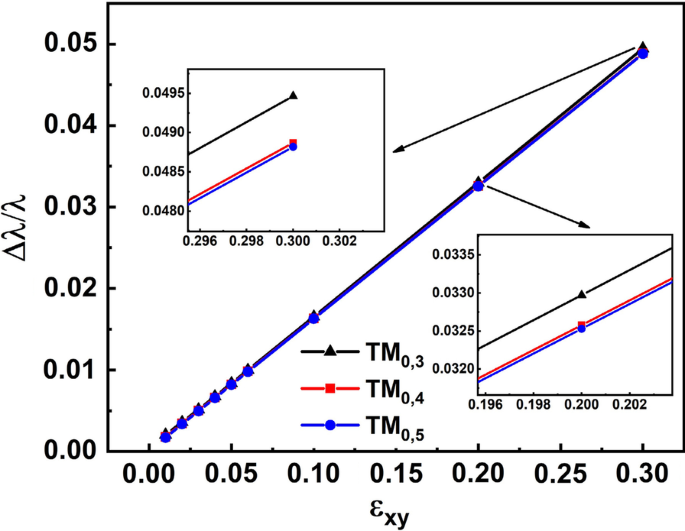
不同模式下 \(\Delta \lambda /\lambda\) 比率随 \(\varepsilon_{xy}\) 变化的线图。插图是 \(\varepsilon_{xy} =0.2\) 和 \(\varepsilon_{xy} =0.3\)

对于较小的方位模数n，硬币悖论SOI对横向磁光效应的增强更为显着。因此，在相同波长范围内，较小的腔会产生较大的横向磁光效应，即较大的波长分裂。为了证实这一结论，盘腔半径R 被设置为一个较小的值，421 纳米。小腔R的透射光谱 =421 nm 如图 5a 所示，与较大腔 R 的相比 =540nm。可以看出，对于较小的腔 R TM0,3 =421 nm 和 TM0,4 对于更大的腔 R =540 nm 均位于约 1550 nm。对于不同的圆盘腔半径，波长分裂随 \(\varepsilon_{xy}\) 变化的线性图绘制在图 5b 中。很明显，较小腔体的波长分裂大于较大腔体的波长分裂，这与我们的预期一致。此外，硬币悖论SOI对横向磁光效应的增强再次得到证实。

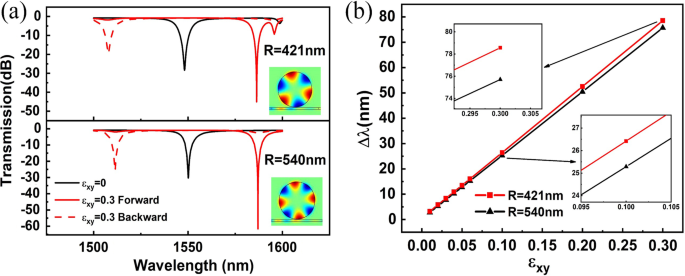
不同半径圆盘腔的透射光谱和波长分裂。 一 来自不同传播方向的光的透射光谱耦合到具有不同半径的圆盘腔中。当 \(\varepsilon_{xy} =0\) 时，插图对应于磁场 z 分量的强度分布。 b 不同半径圆盘腔波长分裂的线性图

众所周知，随着圆盘腔半径的减小，谱线的半峰全宽（FWHM）会增加。较大的 FWHM 一直是主要的无法克服的症结，阻碍了具有较小模型体积的腔体的应用。由 \(\varepsilon_{xy}\) 的变化引起的 FWHM 的变化可以忽略。随着盘腔的半径从 540 nm 减小到 421 nm，FWHM 从大约 9.914 nm 增加到大约 10.811 nm。随着椎间盘腔半径的减小，FWHM 增加了约 0.897 nm。这种线性膨胀可以通过增加分裂得到有效补偿。例如，当 \(\varepsilon_{xy} =0.1\) 时，波长分裂的增加约为 1.130 nm。当 \(\varepsilon_{xy} =0.3\) 时，波长分裂的增加约为 2.850 nm，远大于 0.897 nm。因此，本文提出的光隔离器结构在更小的尺寸下具有更大的应用潜力，更有利于实现更高的光集成度。

结论

总之，设计了一种由 MIM 波导和填充磁光材料的圆盘腔组成的简单片上集成光隔离器。在这种光隔离器结构中，存在新的硬币悖论自旋轨道相互作用，有效地增强了横向磁光效应。此外，对于较小的方位角模式数 n，增强更为显着。基于增强的横向磁光效应，获得了一种高性能的片上集成光隔离器。发现最大 IR 大于 60 dB，IL 约为 2 dB。横向磁光效应在很宽的波长范围内保持强烈。此外，验证了较小腔体具有更大的横向磁光效应，可以有效克服较小腔体引起的谐振谷的展宽。

数据和材料的可用性

支持本文结论的所有数据均包含在本文中。

缩写

SPP：

表面等离子体激元

TSAM：

横向自旋角动量

LSAM：

纵向自旋角动量

SAM：

自旋角动量

OAM：

轨道角动量

SOI：

自旋轨道相互作用

MIM：

金属-绝缘体-金属

IR：

隔离比

IL：

插入损耗

TM：

横磁

Bi：

YIG：掺铋钇铁石榴石

有限元：

有限元法

FWHM：

半峰全宽

EBL：

电子束光刻