电子表面散射对金纳米壳光吸收和散射消光比的影响

背景

金纳米壳由介电核组成，可以是二氧化硅或Au 2S [1, 2] 和一个同心的金壳。由于金的生物相容性 [3, 4]，抗体和靶向部分易于结合到金壳表面 [5]，其共振波长可调谐到近红外区域 [2, 6]，以及称为生物水窗的区域，其中组织透射率最高 [7]，金纳米壳增强的光散射和吸收已在生物医学成像和光热治疗中得到应用 [8, 9]。 Mie 理论对核壳结构的扩展可用于计算单个金纳米壳的光吸收和散射截面 [10]，这两者的总和给出了它的消光截面。由于金纳米壳的厚度通常小于或与大块金中电子的平均自由程相当，约为 37.7 nm [11]，金壳中的电子每单位时间经历更多的碰撞（由传导电子的散射引起的额外碰撞）从壳表面）而不是在散装金中 [12, 13]。据报道，传导电子的表面散射会导致共振峰变宽，这通过测量和计算光谱的拟合得到证实 [6, 14,15,16]，以及单个纳米壳的散射和吸收绝对值的降低理论计算证明了这一点 [17,18,19]。然而，对于基于散射的生物医学成像应用 [9, 20, 21]，其中金属纳米粒子或荧光材料附着在目标组织或细胞上，如果只希望对被研究的组织或细胞进行成像而不对组织或细胞造成热损伤，它重要的是，附着的纳米颗粒在所需波长下具有高散射率和低吸收率。散射和吸收的比率而不是它们的绝对值值得关注的原因是散射和吸收绝对值的降低可以通过将更多的粒子附着到目标组织或细胞来补偿。金属纳米粒子共振光散射在透明投影屏幕 [22,23,24,25] 和光伏 [26,27,28,29,30] 中的应用，也需要在所需波长范围内同时具有高散射和低吸收比.更重要的是，金超材料还要求金呈薄膜形式，作为吸光体可以实现高光吸收[31, 32]，或作为透明导电膜实现高透光率[33,34,35,36]，因此，传导电子的表面散射效应也起作用。因此，研究电子表面散射对金纳米壳的光吸收和散射消光比的影响，可为设计纳米级金相关结构提供一定的指导。

在这项工作中，首先进行模拟，通过考虑有和没有表面散射的情况，研究电子的表面散射对金纳米壳的光吸收和散射与消光之比的影响。结果表明，电子的表面散射增加了光吸收率，从而降低了光散射率，壳厚度越薄，光吸收率增加的幅度越大。然后通过比较测量和模拟的吸收光谱以及消光光谱，对三个样品的吸收增加进行了实验验证。

模拟和实验结果将首先在“结果和讨论”部分显示，然后在“方法/实验”部分提供消光和吸收的光学测量的详细方法，以避免由于描述光学测量。

结果与讨论

通过模拟研究了具有四种不同壳厚度但相同核直径的金纳米壳。金纳米壳包括（80 纳米直径的二氧化硅核）@（15 纳米厚的金壳）、（80 纳米直径的二氧化硅核）@（25 纳米厚的金壳）、（80 纳米厚的金壳）二氧化硅核)@(35nm厚的金壳)，和(80nm直径的二氧化硅核)@(45nm厚的金壳)。

平行入射光线与单个纳米粒子相互作用后，除了直接透射（沿入射光的原始方向传播）之外，光被吸收或散射，这两者的总和称为消光[37] ]。散射、吸收和消光，以截面量化，可以直观地感知为分别由于散射、吸收或消光而从入射光路径上去除的光的面积量，可以通过米氏理论的扩展计算对于核壳结构[10]。然而，将横截面归一化为纳米颗粒的几何横截面更自然，πR ² ，其中 R 是核壳结构的外半径，用于比较不同结构，j的比值 横截面 (j =吸收、散射或消光）到几何横截面被称为 j 效率。

不考虑表面散射效应的消光和吸收效率是通过使用块状金的介电函数 [38] 作为 Mie 理论的输入来计算的，它们在图 1 中显示为红线（实线或虚线）。考虑到表面散射的影响，假设金的介电函数具有描述自由电子行为的德鲁德模型分量 [39]，以及额外的阻尼项 γ 将传导电子的表面散射贡献的 s 添加到体阻尼 γ b 在 Drude 项中给出修正的介电函数 ε sh 代表金壳 [19]:

其中 ε exp 是参考文献 [38] 中金的体介电函数，ω p 是金的等离子体频率，ω 是入射光的频率，i 是虚数。对于图 1 中表面散射效应的计算效率（蓝线、实线或虚线），ω 假设 p 和 γb 分别为 8.55 eV 和 18.4 meV [19]。和 γ s 由 [19] 给出：

其中 v F是金中电子的费米速度，等于1.40 × 10 ⁶ 米/秒 [19] 和 L B是壳内电子的有效平均自由程，由假设台球散射模型推导出来[13]，其中电子从壳的两个表面的反射为镜面反射，由下式给出

其中 r o 和 r i 分别是纳米壳的外半径和内半径。假设周围介质和二氧化硅纤芯的折射率分别为1.5和1.45。

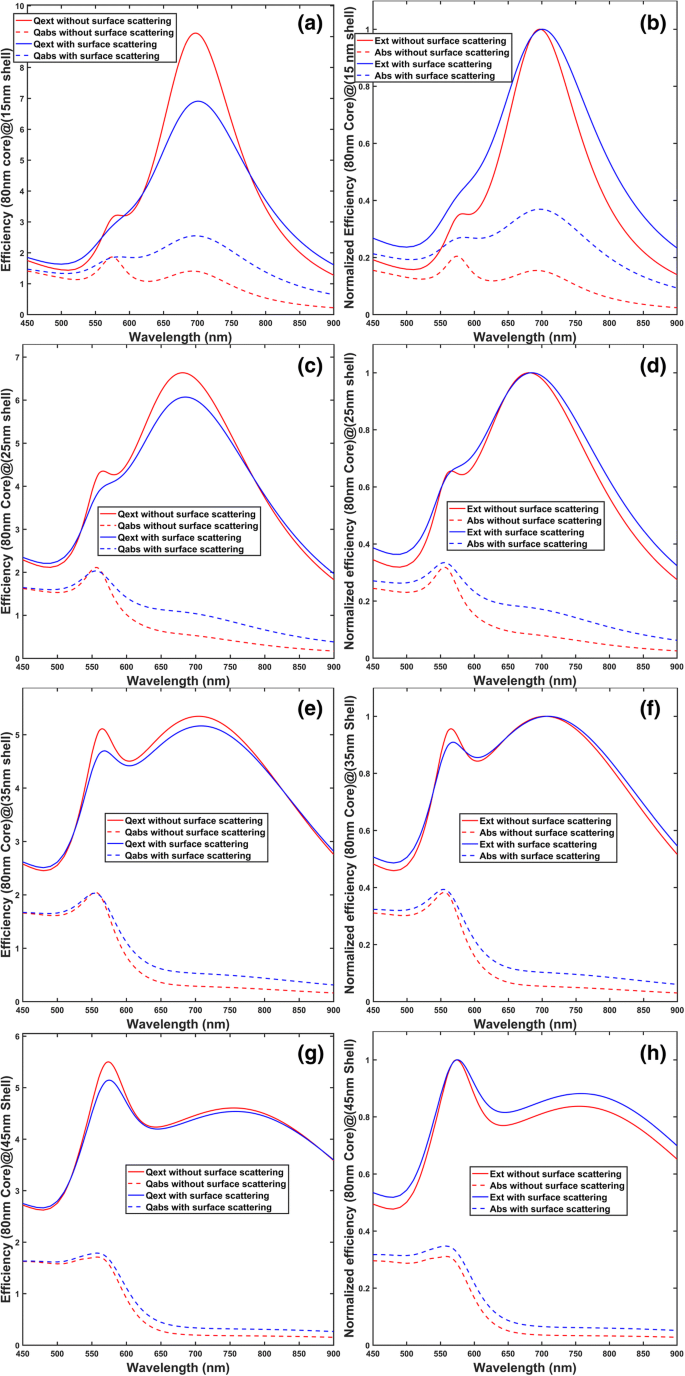
计算消光和吸收效率，考虑和不考虑传导电子的表面散射，其中 Q ext（Ext）代表消光效率（normalized extinction）和Q abs（Abs）代表吸收效率（归一化吸收）。散射效率（归一化散射）是 Q 分机 (Ext) 和 Q 绝对（绝对）。所有计算均采用米氏理论，假设二氧化硅和周围介质的指数分别为 1.45 和 1.5。没有表面散射的金的介电常数来自参考文献 [38]，而具有表面散射的介电常数由方程给出。 (1)~(3). 一 和 b 用于（80 纳米直径的二氧化硅核）@（15 纳米厚的金壳）。 c 和 d 用于（80 纳米直径的二氧化硅核）@（25 纳米厚的金壳）。 e 和 f 用于（80 纳米直径的二氧化硅核）@（35 纳米厚的金壳）。 g 和 h 用于（80 纳米直径的二氧化硅核）@（45 纳米厚的金壳）。左列，即 a , c , e , 和 g , 是根据米氏理论计算的相应效率。右列，即 b , d , 和 f ，是归一化到偶极共振峰（700 到 800 nm 之间的共振峰）的效率，以及 h 效率归一化为四极共振峰（550 到 600 nm 之间的峰）

从图 1 的左列，对于四种壳厚度，在包括表面散射效应后，观察到消光和吸收光谱都经历了加宽，并且在消光光谱幅度减小的同时，吸收光谱增加了在偶极共振峰（700 到 800 nm 之间的峰）处有很多变化，而在四极共振峰（550 到 600 nm 之间的峰）似乎没有变化。在包含表面散射效应之后，消光效率大小的降低和吸收效率大小的增加导致吸收与消光比的增加。这由图 1 的右列证实，其中观察到在偶极和四极峰位置处吸收增加（即蓝色虚线在红色虚线上方）。直观地说，在考虑表面散射效应后，随着壳厚度的增加，吸收率的增加变得不那么显着，如图 1 中的（b）、（d）、（f）和（h）所示。这是因为壳层越厚，电子与壳层表面碰撞的频率越低，即表面散射效应降低。表 1 也证实了这一现象。对于每个壳厚度，有（无）表面散射的吸收率，由蓝色（红色）虚线下的区域与蓝色（红色）实线下的区域的比率计算, 列于表 1。为了进一步研究吸收率增加背后的机制，近电场振幅平方的空间分布|E | ² 绘制在图 2 中。在图 2 中，可以观察到 |E | ² s 没有表面散射的计算比有表面散射的要大，可以这样解释：假设表面散射生效，传导电子与金块相比，从壳表面受到更多的碰撞，因此传导电子的平均振荡幅度为减少，导致|E 减少 | ² s .并且由于传导电子与壳表面的碰撞导致能量损失为热量，因此在包括表面散射效应后吸收率增加。

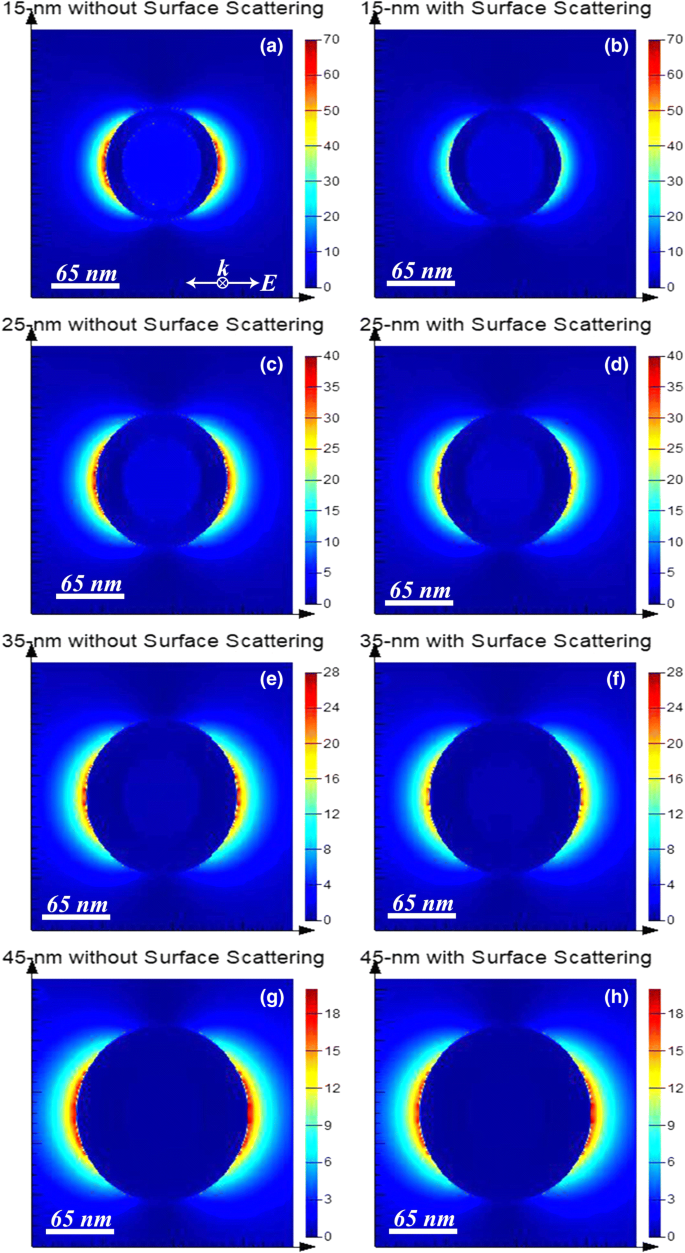
近电场幅度的平方|E | ² 图 1 中所示的四种结构在其相应的偶极共振峰值波长处的绘图。 一 和 b 在 700 nm 处绘制（80 nm 直径的二氧化硅核）@（15 nm 厚的金壳）。 c 和 d 在 684 nm 处绘制（80 纳米直径的二氧化硅核）@（25 纳米厚的金壳）。 e 和 f 在 706 nm 处绘制（80 纳米直径的二氧化硅核）@（35 纳米厚的金壳）。 g 和 h 在 756 nm 处绘制（80 纳米直径的二氧化硅核）@（45 纳米厚的金壳）。左列，即 a , c , e , 和 g , 显示 |E | ² 使用参考文献 [38] 中大块金的介电常数计算。右列，即 b , d , f , 和 h , 显示 |E | ² 用金的介电常数计算，通过方程修改表面散射。 (1)~(3)。入射光的偏振和传播方向在所有图中都相同，如a所示 .模拟由“FDTD Solutions”软件进行，三维网格覆盖区域的网格尺寸为1 nm

根据材料的可用性，对三种不同壳厚度但核直径相似的纳米壳的吸收和消光进行了实验测量：（80 纳米直径的二氧化硅核）@（16 纳米厚的金壳），（79 纳米直径）二氧化硅核）@（29 纳米厚的金壳）和（88 纳米直径的二氧化硅核）@（36 纳米厚的金壳），其 TEM 图像如图 3 所示。图 4 显示了比较三种纳米壳的实验测量和理论模拟结果之间的差异。从图 4 中可以看出，考虑到表面散射效应的计算吸收截面与所有三个纳米壳的测量结果非常吻合，而如果表面不考虑散射效应。

用于实验测量的三个金纳米壳的 TEM 图像。 一 80 纳米直径的硅胶核，16 纳米厚的金壳。 b 直径 79 nm 的二氧化硅核，29 nm 厚的金壳。 c 88 纳米直径的硅胶核，36 纳米厚的金壳。详细的表征信息在支持信息中提供

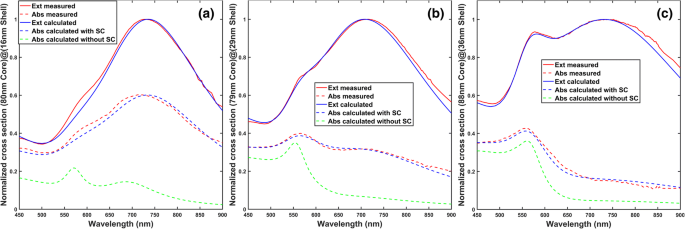
测量和计算吸收光谱之间的比较，考虑和不考虑传导电子的表面散射。所有计算均采用米氏理论。周围介质是折射率为 1.5 的 PVA（聚乙烯醇）。请注意，我们实验中纳米壳的周围介质（PVA，n =1.5) 与支持信息中提供的表征表中的不同，即水。包覆纳米壳的表面活性剂可以忽略不计，因为表面活性剂是薄聚合物并且具有与 PVA 周围介质相似的折射率。在计算中假定二氧化硅的折射率为 1.45。没有表面散射的金的介电常数来自参考文献 [38]，而具有表面散射的介电常数由方程给出。 (1) 和 (4)。在所有图例中，“Ext”是消光的缩写，“Abs”是吸收的缩写，“SC”是表面散射的缩写。各图中，“Ext计算”和“Abs计算得到的SC”是根据表2拟合参数计算得到的消光和吸收光谱，“Abs计算不SC”是不考虑粒径分布和表面积计算得到的吸收截面散射。 一 （80 纳米直径的二氧化硅核）@（16 纳米厚的金壳）。 b （79 纳米直径的二氧化硅核）@（29 纳米厚的金壳）。 c (88nm直径硅胶核)@(36nm厚金壳)

为了将计算的消光（蓝色实线）与实验测量的消光（红色实线）拟合，如图 4 所示，额外阻尼 γ 的表达式 s 在方程式中。 (1) 由于表面散射，由方程给出。 (4) 如下所示 [15]，而不是等式。 (2).

其中 A 是一个无量纲的拟合参数和一个更大的A 表示较大的阻尼和 d s 是壳厚度。拟合参数A 受表面电子密度、界面效应、粒子各向异性、量子力学计算等多种因素影响，其值已显示为0.1到2以上[40, 41]。请注意，我们可以写出等式。 (2) 转化为方程的形式。 (4) 比较A的理论值 通过台球散射模型预测到实验拟合的结果，首先计算L的值 方程式中的B (2) 使用方程。 (3)，然后写L 方程式中的B (2)变成d的形式 s/A ，如方程式所示。下面的（5a）至（5d）：

写

那么

哪里

请注意，当壳厚度小于总半径的 25% 时，公式(5d) 给出一个 A 值约为 0.5 [13]。图4所示三种纳米壳的计算光谱拟合参数值列于表2中。

图 4 中计算的消光和吸收光谱归一化为偶极峰，已经考虑了表面散射和尺寸分布。对于每个纳米壳，核直径和壳厚度的标准偏差分别通过将表 2 中所示的核直径和壳厚度值与支持信息中提供的表征表中给出的变异系数相乘来计算。配件中使用的芯径大于特性表中给出的值。这是因为二氧化硅球体的尺寸在 TEM 检测下会缩小 [42, 43]，并且壳厚度是通过从表征表中给出的总直径中减去表 2 中的核心直径来获得的。计算出的消光光谱的峰宽被调整到与测量的匹配，然后，相应的吸收光谱用调整后的参数计算。 A 的值 台球散射模型预测的三个纳米壳分别为 0.60、0.52 和 0.53，如果方程。 (5d) 被应用，明显小于拟合的 A 表 2 中列出的三个纳米壳的值分别为 1.33、1.67 和 1.33。由于 A 的较大值 在方程式中(4) 意味着更大的自由电子阻尼，观察到传导电子的实际阻尼大于台球散射模型预测的阻尼，其中额外的阻尼可能是由于壳与周围介质之间的化学界面以及二氧化硅核 [44, 45]、表面电子密度、粒子各向异性和量子力学计算，如前所述。通过观察支持信息中表征表中的 TEM 图像可以排除不连续壳的可能性。请注意，在拟合过程中已经考虑了由于纳米壳尺寸分布引起的峰展宽，即 A 的拟合值 不考虑尺寸分布。关于如何测量消光和吸收的详细信息，请参见“方法/实验”部分。

方法/实验

在本节中，对于图 4 中研究的纳米壳，描述了如何将它们分散到 PVA（聚乙烯醇）薄膜中，以及如何从纳米颗粒分散的 PVA 薄膜的光学测量中推导出这些纳米壳的消光和吸收。

图 4 中研究的三个纳米壳，即（80 纳米直径的二氧化硅核）@（16 纳米厚的金壳）、（79 纳米直径的二氧化硅核）@（29 纳米厚的金壳） , 和 (88-nm-diameter silica core)@(36-nm-thick gold shell)，在下面的讨论中为了方便起见分别缩写为 16-nm、29-nm 和 36-nm 金纳米壳，分别是直接从专业公司 nanoComposix 购买，其特性表显示在支持信息中（附加文件 1）。

纳米壳在接收后分散在水中，其中 16 纳米金纳米壳的浓度为 0.02 毫克/毫升，另外两个金纳米壳的浓度为 0.05 毫克/毫升。对于 16-nm、29-nm 和 36-nm 金纳米壳，分别使用 34、25 和 34 mL 的溶液来制备纳米颗粒分散的 PVA 薄膜。在将收到的纳米壳溶液与 PVA 粉末（80% 水解，Sigma-Aldrich）混合之前，通过离心和重新分散将每种纳米壳溶液浓缩至 9 mL。然后将 0.9-g PVA 粉末添加到每个浓缩的纳米壳溶液中，并将混合物搅拌 2 小时。此后，每个搅拌的溶液在真空室中脱泡，然后倒入 5 × 5 cm ² 玻璃模具，将模具置于通风橱中，让溶液自然干燥。溶液干燥后，将 PVA 薄膜从玻璃模具上撕下，如图 5 所示。同样制成没有任何纳米颗粒分散的纯 PVA 薄膜，不同之处在于混合了 9 mL 水而不是纳米壳溶液。 PVA粉末。

一 分散有 16 纳米金纳米壳的薄膜。 b 分散有 29 纳米金纳米壳的薄膜。 c 分散有 36 纳米金纳米壳的薄膜。 d 纯PVA薄膜

消光截面σ 纳米壳的外部与直接透射率 T 有关 通过 Beer-Lambert 定律制备纳米壳薄膜 [44]：

其中 N 是纳米颗粒的面密度，即每单位面积的纳米壳数（注意该面积垂直于入射光的传播方向）。直接透射率T 通过将测得的分散有纳米壳的 PVA 薄膜的直接透射率归一化为没有分散任何纳米颗粒的纯 PVA 薄膜的直接透射率而获得。所以N ∙ σ ext 由以下等式给出：

注意不是 σ 分机，只有 N ∙ σ ext 源自实验测量，因为重要的是频谱的整体形状。在图 4 中，N ∙ σ ext 被归一化，使得 N 的最大值 ∙ σ 谱外为1。

吸收截面σ 由于吸收 ΔI，单个纳米壳的 abs 与平行入射光束的强度损失有关 根据 Beer-Lambert 定律 [44]：

其中我 0为入射光强度。

因此，下一步是通过实验发现仅由于纳米颗粒的吸收而导致的入射光衰减。方程 (8) 假设粒子是纯吸收的 [44]。对于同时吸收和散射光的纳米粒子，方程。 (8) 由于多次吸收而无效。对于此类纳米粒子的集合，当入射光首先撞击纳米粒子时，一些光线会被吸收，而另一些则会被散射。但是对于这些散射光线，当它们在离开纳米粒子整体的过程中击中更多的纳米粒子时，其中的一部分会再次被吸收，从而导致多次吸收。散射光的多次吸收表明，通过测量分散有纳米壳的 PVA 薄膜未吸收的光总量，N ∙ σ 根据方程得出的绝对值。 (8) 倾向于高估吸收。然而，由于我们实验中的 PVA 薄膜很薄（约 0.3 毫米），并且纳米壳的浓度不高，因此假设大部分光经历单次散射（因此单次吸收）[25]。在此假设下，使用积分球测量未被分散有纳米壳的 PVA 薄膜吸收的光总量的实验装置如图 6 所示。图 6 T 1、T 2 或 R 与被困在积分球中的光量成正比，即未能从右侧开放端口射出的光量。在下面的讨论中，假设 T 1、T 2、R 与积分球收集的光强成正比，具有相同的系数α .

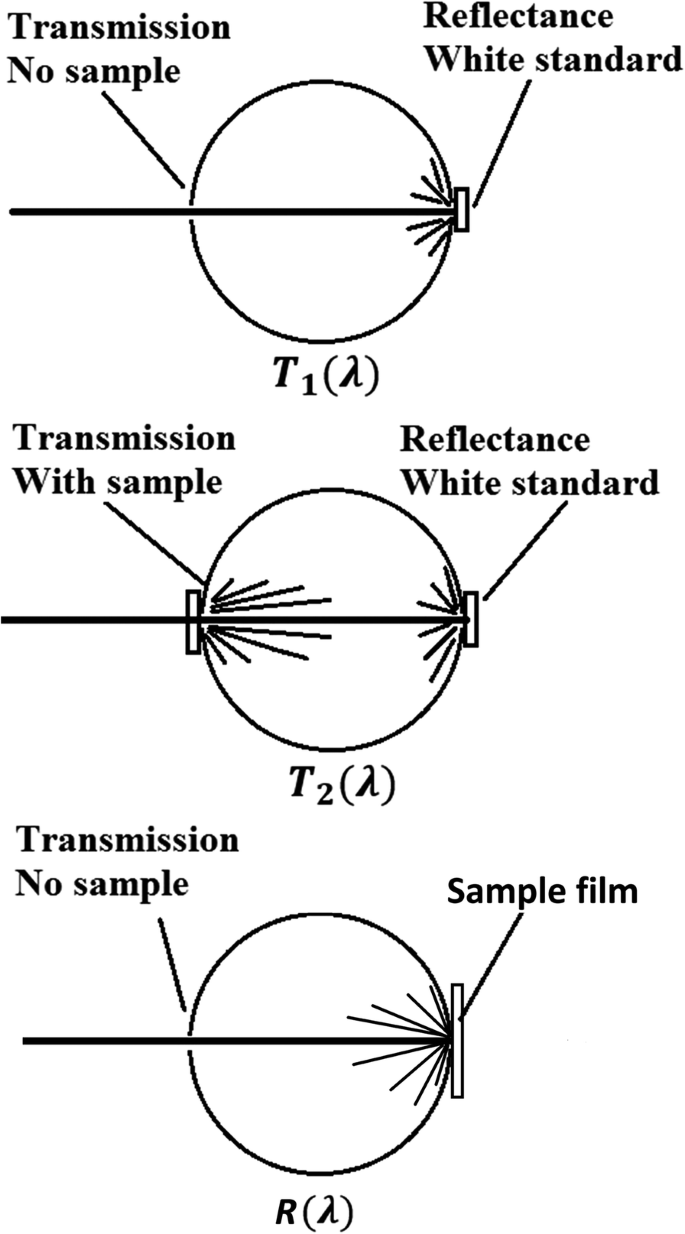
测量吸收的实验装置。直接测量的值为T 1(λ ), T 2(λ ) 和 R (λ ) 其中 T 我 (i =1, 2) 或 R (λ ) 与被困在积分球中的光量成正比。从这些测量值推导出吸收。此设置是参考 [22] 中报告的设置的简化版本

等式（8）可以重新排列为 \( \left({I}_0-\Delta {I}_{\mathrm{abs}}\right)={I}_0{e}^{-N\bullet {\ sigma}_{\mathrm{abs}}} \)，其左侧代表入射光穿过样品膜后未被吸收的总光量。根据图 6 中的测量结果，我们可以写出以下等式：

代入方程。 (9) 和方程。 (10) 转化为 \( \left({I}_0-\Delta {I}_{\mathrm{abs}}\right)={I}_0{e}^{-N\bullet {\sigma}_{ \mathrm{abs}}} \)，并且除了 N 之外还包括一个噪声项 ∙ σ abs，可以得到如下等式：

其中噪音 来自 PVA 矩阵。由于入射光在空气/PVA 界面处的第一次反射，大约 4% 的入射光永远不会进入薄膜（根据菲涅尔方程，在两种不同指数 n<介质的界面处法向入射时/i> 1（空气=1）和n 2（PVA=1.5），光的反射率R 由 \( R={\left|\frac{n_1-{n}_2}{n_1+{n}_2}\right|}^2 \)) 给出，因此方程。 (11) 修改为