表面状态和铝摩尔分数对 AlGaN/GaN HEMT 中表面电位和 2DEG 的影响

介绍

高频和高功率应用是 GaN 材料的两个主要特性，在过去的 30 年中得到了研究 [1, 2]。 AlGaN/GaN 结构的主要优点之一是即使在势垒层中没有有意掺杂，也可以在 AlGaN-GaN 界面的三角形势阱中形成 2DEG [3, 4]。已经很好地证明了在 AlGaN/GaN 结构的 AlGaN 层中存在自发极化和压电极化[3]。这种极化会在 AlGaN 势垒层的底部和顶部产生两个相反的电荷层。这些极化片电荷本身不足以在 AlGaN-GaN 界面形成三角形势阱。为了解决这个问题，Ibbetson 等人. [5] 建议在 AlGaN 层的表面必须存在正电荷层。由于表面施主态的电离（从导带 1.42 eV 与 1.35 × 10 ¹³ cm ⁻² )在表面[6]。

Vetury 等人. [7] 使用电位探针作为浮栅研究了这些表面状态的影响。已经研究了表面状态对 AlGaN/GaN HEMT 的 DC 和 RF 性能的影响 [8, 9]。纳米级肖特基栅极行为讨论了由于表面施主状态 [10] 在非门控区域中形成的虚拟栅极。固定表面施主状态用于分析 HEMT [11] 中的自热效应。 Longobardi 等人. [12] 进行了第一次 TCAD 模拟，以研究表面施主状态对 AlGaN/GaN MISFET 直流特性的影响。为了在 TCAD 模拟中激活这些表面施主状态，Bakeroot 和其他人引入了不同的模型 [13, 14]。由于在 AlGaN 表面的非门控区域中形成虚拟栅极，因此漏极/源极电阻也取决于栅极偏置。 Pradeep 等人. [15] 基于 AlGaN/GaN HEMT 的线性区域直流特性开发了迁移率和电阻提取程序。 Meneghesso 等人. [16] 讨论了表面状态作为陷阱捕获 AlGaN 表面上的高密度空穴层以补偿 2DEG 中的电子。当这些陷阱被具有负栅极偏压的电子占据时，在 AlGaN 层顶部可用的表面施主陷阱会改变器件的电学行为 [17]。表面施主陷阱和 2DEG 电子之间的关系也通过 TCAD 模拟通过采用时间相关的传输现象进行了讨论 [18]。尽管已经探索了不同的表征技术，Tapajna 等人。 [19] 使用阈值瞬态方法来研究界面受体陷阱，但表面供体陷阱表征仍未探索。还讨论了作为供体的表面陷阱的广泛计算建模方法 [20]。古克曼等人. [21] 讨论了如果表面施主密度大于极化电荷浓度，那么电子就会转移到AlGaN-GaN界面，从而使2DEG进入通道。

上述讨论的文献报道了 AlGaN/GaN 异质结构的许多相关方面，但没有考虑表面供体（浓度 + 能量）和铝浓度对二维电子浓度的贡献的综合影响。很明显，铝的百分比主要负责AlGaN势垒层中的极化电荷[3]。

为了提供对这种效应的适当物理理解，我们在目前的工作中涵盖了以下研究（i）随着表面施主陷阱从深到浅的变化以及 AlGaN 势垒层中铝百分比的变化，对二维电子浓度的影响， (ii) 表面陷阱和铝百分比对表面电位的影响；(iii) 表面施主陷阱和铝百分比对AlGaN-GaN界面三角势阱的影响。

方法部分和模拟设置

二维设备模拟是使用 Synopsys 的 Sentaurus TCAD 版本 L-2016.12 [22] 进行的。我们通过再现 AlGaN/GaN HEMT 异质结构的实验结果来校准 TCAD 模拟装置 [15]，如图 1b 所示。

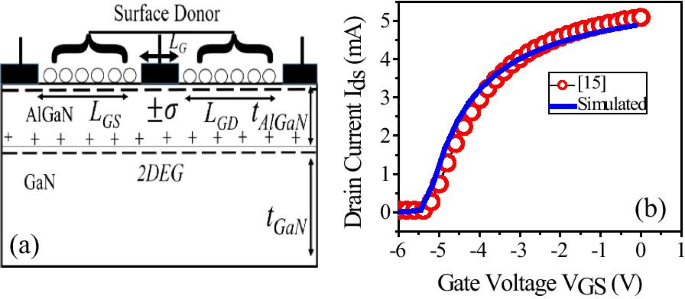
一 Al 摩尔分数为 28% 的二维模拟结构示意图。 b 通过重现报告的实验结果校准模拟装置 [15]

校准后的器件在 2 μm GaN 缓冲层的顶部具有 30 nm AlGaN 势垒层。肖特基栅极长度 (L G) 1 μm 对称放置在 AlGaN 势垒层的顶部。从栅极到漏极/源极 (L GD/L GS) 每个尺寸为 2.5 μm，器件宽度为 150 μm。

模拟平台处理三个条件（泊松条件、电子和空穴连续性条件），用于监督半导体行为。

还包括自洽漂移和扩散 (DD) 传输模型。 Lombardi 迁移率和 Philip 统一迁移率模型被调用以促进由于电场和掺杂引起的迁移率下降。此外，Auger 和 SRH（Shockley-Read-Hall）重组模型与 Fermi-Dirac 统计一起使用。激活 Slotboom 模型以遇到重掺杂漏源扩展区的带隙变窄。由于这种结构有两层，我们正在改变AlGaN势垒层中的铝百分比，根据方程[3]引入极化电荷：

其中 P SP 是自发极化，e 33 和 e 31 是压电系数，C 33 和 C 31 是弹性常数，a 是晶格常数，x 是铝的摩尔百分比。

极化电荷的变化 ± σ AlGaN (x ) 的铝百分比如图 2a [3] 所示。一旦计算出极化电荷，就可以求解泊松方程。在 AlGaN-GaN 界面，导带突然变化并形成一个狭窄的 (1-4 nm) 三角势量子阱，电子在其中积累。由于该量子势阱非常窄，因此降低的态密度变得占主导地位。薛定谔量子方程解释了量子势阱，但对于较大的 HEMT 器件来说很难求解。为了捕捉量子势阱行为，我们在 Sentaurus TCAD 中调用了 eQuantumpotential 模型，该模型激活了密度梯度量子校正模型 [23]，并为更大的 HEMT 器件（功率 HEMT 器件）提供了与薛定谔量子方程密切匹配的结果。密度梯度量子模型降低了 2DEG 中电子密度的峰值，并且峰值也偏离了 AlGaN-GaN 界面。因此，这减少了界面散射机制并提高了通道中的迁移率，见图 2b [20]。密度梯度量子模型在正态密度公式中引入了一个额外项Λ，如：

其中 N C 是有效态密度，F 1/ 2 是 1/ 阶费米积分 2、E F 是电子的准费米能量，E C 是导带边缘，kT 代表电子的热能。 Λ 计算公式为：

其中 ħ =h /2π , h 是平板常数，m n 是电子的有效质量，γ (γ =1.28) 是拟合参数，n 是电子密度。

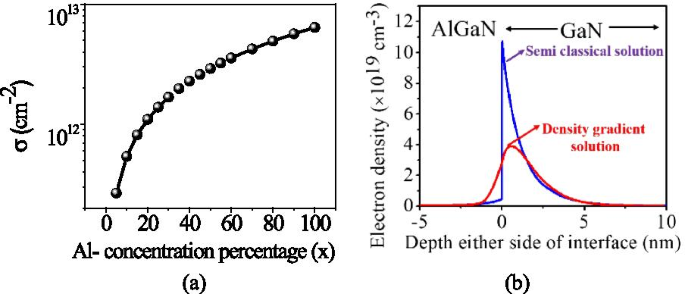
一 极化片电荷随 AlGaN 阻挡层中铝浓度的变化 [3]。 b 量子俘获对2DEG电子密度的影响

表面陷阱被引入作为施主状态 (+ σ D)在AlGaN势垒层的表面，如图1a，模拟在300 K温度下进行，初始铝浓度为28%时进行校准。

模拟结果与讨论

铝百分比和表面陷阱对 2DEG 密度的影响

在不施加偏压条件下模拟该装置以研究 2DEG 电子密度。当我们专注于 2DEG 电子密度时，对于供体状态的所有能量，直到供体陷阱浓度的某个值（相对较低的值），电子密度（即 Region1）没有显着变化。 2DEG 电子密度随表面供体浓度成比例变化（在 Region1 到 Region2 之间）。在表面施主陷阱的某个阈值之后，电子密度（即区域 2）再次没有出现变化，见图 3a-d。这种机制可以解释如下：

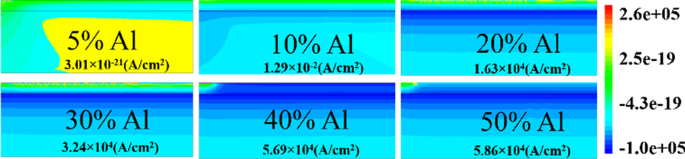
一 –d 不同铝百分比的 2DEG w.r.t 表面供体浓度和能量（从浅的 0.2 eV 到深的 1.4 eV）中电子层密度的变化。 e 器件中不同的电荷分布和电场取向

(i) 区域 1 的 AlGaN 势垒层的导带与表面的费米能级有较大的间隙。随着供体陷阱浓度开始从较低值增加到较高值，在过渡期（区域 1 到区域 2 之间），导带开始按比例向费米能级移动。因此，2DEG 浓度开始从较低值增加到较高值。在过渡期（区域 1 到区域 2 之间）导带开始按比例向费米能级移动，因此施主表面能也向费米能级移动。对于区域 2，一旦施主浓度超过阈值，导带弯曲开始，施主陷阱的能量固定费米能级。由于费米能级钉扎，所有施主态都被电离并为 2DEG 三角量子势阱贡献电子。一旦施主态的能量固定在费米能级上，电子密度就不会发生显着变化。 (ii) 为了在器件中找到电荷中性，表面施主态对于对抗 2DEG 中的电子至关重要。随着表面施主态的增加，电场开始从表面增加到 2DEG 量子阱。该电场与极化片电荷 (± σ 氮化铝）。当外电场开始超过内电场时（由于 ± σ AlGaN)，它降低了表面的导带，从而为 2DEG 势阱贡献更多电子，见图 3e。当铝的百分比从 5% 增加到 50% 时，极化片电荷密度也成比例增加，这会导致高内电场（由于极化）。为了克服这个内部电场，需要更高浓度的表面施主陷阱。因此，过渡区域被移动（从 10 到 130 次，10 ¹¹ cm ⁻² ) 对于更高的供体陷阱浓度值，其中 2DEG 电子密度与供体陷阱浓度成比例变化，图 3a-d。相对于表面供体（浓度 + 能量）的每个铝百分比的 2DEG 浓度绘制在图 4 中。尽管当供体陷阱从浅层 (0.2 eV) 变为所有百分比的铝时，2DEG 电子浓度的模式是相同的到深（1.4 eV）（图5），2DEG电子密度从深到浅的变化仍然非常显着。在 5% 铝浓度的情况下，供体陷阱从深 (1.4 eV) 到浅 (0.2 eV)，它对势阱的贡献不大。作为极化电荷浓度 (± σ ) 的数量级为 10 ¹¹ cm ⁻² 对于 5% 的铝，见图 2a，这些极化电荷导致的电场不足以使导带偏移低于费米能级，因此在 AlGaN-GaN 界面结构的 GaN 侧没有形成 2DEG 三角形势阱。同样明显的是，即使对于更高浓度的表面施主陷阱，电子密度的饱和也不会发生，如图 2 和图 5 所示。如图 4a 和 6 所示。对于 10% 的铝百分比也是如此，如图 4b 所示。对于 20% 及以上，极化电荷 (± σ) 浓度大于 10 ¹² cm ⁻² .所以内部电场足够大，可以将导带偏移拉到费米能级以下，因此它形成了 2DEG 三角形量子势阱，见图 6b、c。所以对于20%及以上的铝百分比，2DEG电子密度接近 ~ 10 ¹³ cm ⁻² 对于浅供体陷阱，如图 4c 所示。对于20%、30%及以上的铝浓度，三角阱中电子的贡献密度为1 × 10 ¹³ 到 3 × 10 ¹³ cm ⁻² .图 5a、b 描绘了当供体陷阱能量从 1.4e 变为 0.2 eV 时三角阱中电子密度的百分比变化。当我们从 5% 到 50% 的铝百分比时，2DEG 浓度的变化从 10.89 倍显着降低到 1.08 倍，并在超过 30% 时达到饱和。

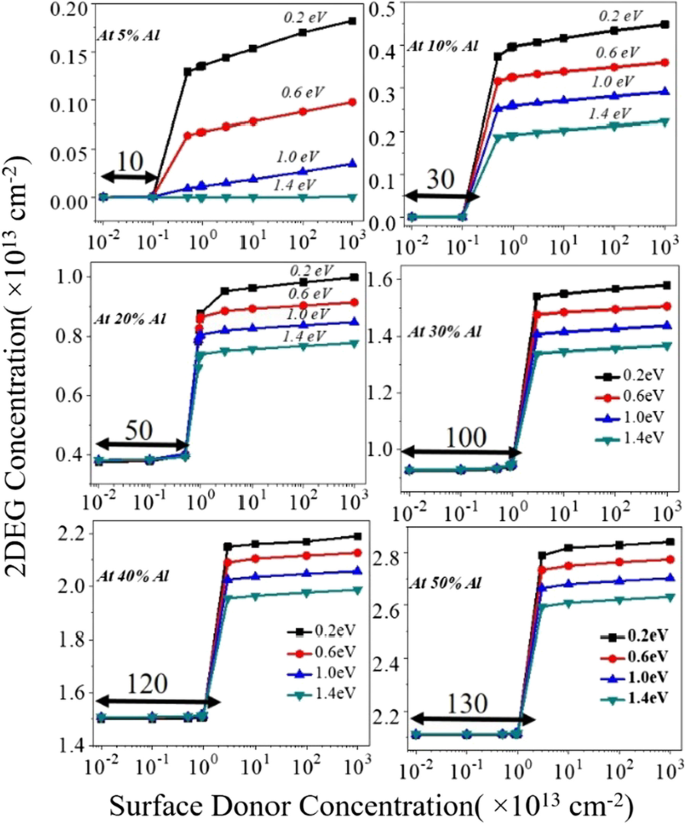
相对于导带，单个铝百分比对施主表面陷阱从深到浅的变化

一 当表面施主相对于导带从深能级变浅时，Al 浓度的 2DEG 电子密度的对数百分比变化。 b 线性刻度

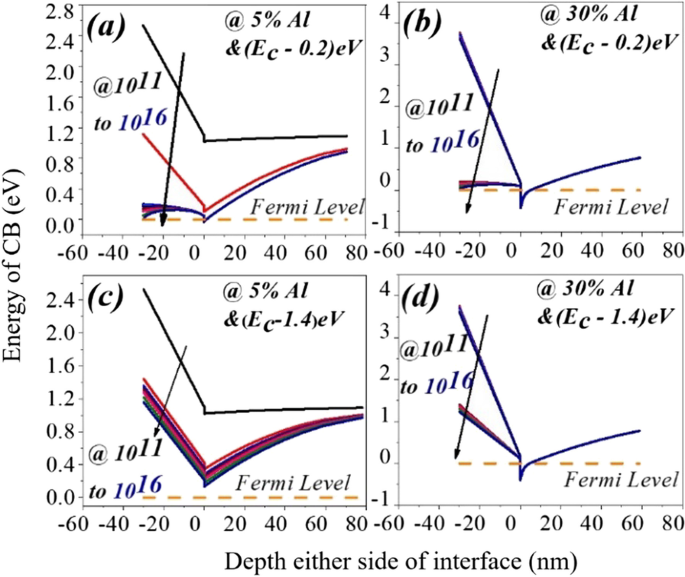
一 , c 5% 铝和 b 的 AlGaN-GaN 界面两侧的导带变化 , d 对于 30% 铝。深能级表面陷阱不向势阱和表面贡献电子和正电荷，使得导带斜率更高。即使对于深施主表面态 (1.4 eV)，30% 的铝也会形成 2DEG 势阱。对于 5% 的铝来说，情况并非如此

铝百分比和表面陷阱对表面电位的影响

一些文献讨论了由于铝百分比变化引起的表面电位变化 [29]。但是他们没有考虑表面施主陷阱对表面电位的影响。在这里，我们报告了由于表面供体陷阱引起的表面电位变化，在能量和浓度方面，见图 7a。在本研究中，我们将表面供体浓度从 1 × 10 ¹² 到 1 × 10 ¹⁶ 和表面供体能量从 0.2 到 1.4 eV。已从图 6b 计算出表面电位。表面电位稳定在 3.7 eV 附近（表面供体浓度为 1 × 10 ¹² ) 和 3.6 eV（表面供体浓度为 1 × 10 ¹³ ）。该表面电位不依赖于表面施主陷阱的能量，因为它的值较低。随着表面施主从浅层 (0.2 eV) 变深 (1.4 eV)，表面电位线性增加。随着表面电位下降，2DEG 电子浓度将增加，因为表面电位随表面施主陷阱能量线性变化。铝百分比对表面电位也有很大影响。铝百分比从5%增加到50%，电子浓度从7.79 × 10 ¹¹ 到 2.75 × 10 ¹³ .当铝百分比从 5% 变为 50% 时，表面电位也会从 0.49 eV 增加到 0.576 eV，见图 7b。因此，表面施主陷阱浓度和能量以及铝浓度对表面电位有很大影响。

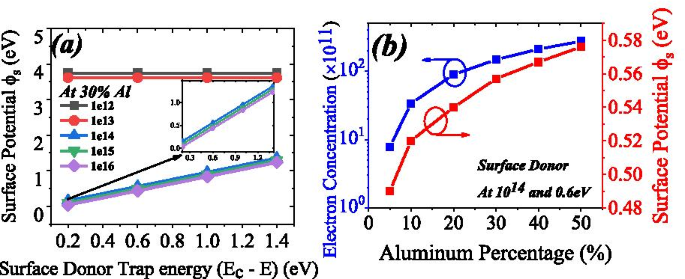
一 相对于表面施主陷阱能量的表面电位变化。在较低浓度（小于 1e14）下，表面电位没有显着变化。表面施主浓度高于 1e13，表面电位与表面施主能量成正比变化。 b 2DEG中的电子浓度从7.79 × 10 ¹¹ 变化 到 2.75 × 10 ¹³ 铝百分比从 5% 变为 50%（蓝线）。表面电位从铝百分比的 5% 到 50% 变化约 0.1 eV

铝百分比和表面陷阱对传导带和 2DEG 势阱的影响

电离表面陷阱为 AlGaN 表面的势阱和正片电荷贡献电子 [6]。在铝浓度为 5% 的情况下，随着陷阱从浅能级深入，电离表面陷阱的数量越来越少。因此，电离表面陷阱对三角形势阱和表面正片电荷贡献较少的电子。 2DEG 中较少量的正电荷和电子浓度不能提供足够的外部电场，因此，AlGaN 层中导带的斜率变得更大，如图 6 所示。这对于铝也是如此，10%在 AlGaN 阻挡层中。来自表面施主态的自由电子驻留在 2DEG 势阱中，它们中和了出现在 AlGaN 表面的正电荷。该电子片电荷由[24]计算：

其中 d 是 Alx 的厚度 Ga(1−x )N 阻挡层，φ b 是肖特基势垒，E F 是费米能级，ΔE C 是 AlGaN-GaN 界面处的导带偏移。从方程很明显。 (4) 电子片电荷密度与导带偏移和极化电荷成正比，极化电荷是铝百分比的函数。当我们将铝百分比从 10% 增加到 50% 时，导带偏移增加 [25]，因此由于能级数量的增加，2DEG 中的电子密度增加，见图 8。器件的内部电场，当铝浓度为 20% 及以上时，导带斜率足以构建三角形势阱，即使对于深能级 (1.4 eV) 表面陷阱能量和较低的表面施主陷阱浓度，如图 6b、d 所示.

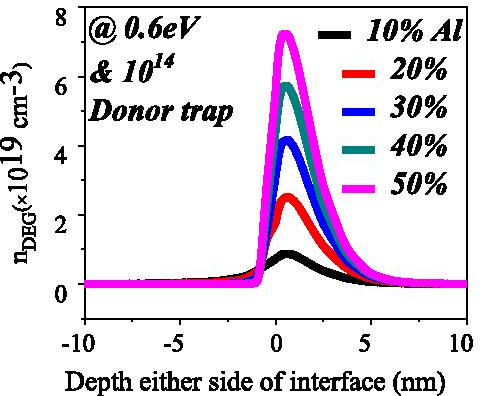
不同铝浓度在固定供体浓度和能量下三角量子势阱中的电子密度

重要的是观察在费米能级 ((E F − E) eV)，其中 E 是费米能级以下的能量。三角量子势阱中的两个重要参数是费米能级以下势阱的深度和费米能级下势阱的宽度。二维区域中电子的限制称为 2DEG 量子片。态密度 N (E ) 是 2DEG 量子势阱的重要特征之一。二维量子阱的态密度定义为[26]：

其中 m* 是电子的有效质量，L X 是井的宽度。二维阱中的这种状态密度看起来像一个阶跃函数。

占据态的数量取决于费米能级。例如，如果费米能级高于 E 1 但小于 E 2;那么只有 E 1个子带被填充。如果费米能级高于 E 2，但小于 E 3、然后是两个较低的子带E 2 和 E 1 充满电子，如图 9b 所示。这意味着如果界面处的能量随着费米能级变得更深，那么预计只会有大量电子。在 AlGaN/GaN 异质结构中，能量间距减小 ((E 2 − E 1)> (E 3 − E 2)) 对于更高的子带 [27]。随着子带能量的增加，它们之间的差异变得可以忽略不计并且看起来是连续的。波函数的严格正确解同时包含泊松方程和薛定谔方程。但是密度梯度模型生成的结果与薛定谔方程近似相等。在量子势阱中，能级是量化的，因为该势阱在 AlGaN-GaN 界面的 GaN 侧形成长达几纳米的长度。费米能级以下的更深的凹口肯定会有更多的量化能级。费米能级以下的量化能级被占用。因此，费米能级以下的能量越深，2DEG 中的电子浓度就会越高。从图 9a 可以清楚地看出，当铝百分比增加时，费米能级以下的能级变得更高，因为极化电荷增加，因此内部电场使缺口变深。就表面供体能量而言，从前面的讨论中可以明显看出，当表面陷阱变深 (1.4 eV) 时，这些表面供体的电离降低。因此，电场是由于表面的正电荷而产生的，这些表面施主贡献给 2DEG 的电子不足以克服内部电场。因此，极化电荷在电场方面的影响减少，这导致费米能级以下的能级减少。一个例外是 5% 的铝浓度，从图 10a 中可以清楚地看出 E 的值 F − E 为负，因为费米能级假设为零能级，对于深施主陷阱（> 0.9 eV 到 1.4 eV），这意味着能量 E 高于费米能级（未形成 2DEG）。对于较浅的表面供体陷阱（<0.9 eV 到 0.2 eV），E 的值 F − E 为正，这意味着 E 的值 低于费米能级。对于其余的铝浓度（10% 到 50%），E 的值 F − E 为正，表示 E 的值 低于费米能级，并且所有类型的表面施主能量（从 0.2 eV 到 1.4 eV）都在形成 2DEG 缺口。从图 11a 中可以看出，能量的百分比变化 E 铝在超过 20% 铝浓度时饱和，这也与图 5 一致。当表面供体陷阱能量从深到浅变化时，在 20% 铝浓度后，低于费米能级的凹口深度没有显着变化。图 11b 还描绘了高达 10% 的铝摩尔分数没有明显的电流。当表面供体能量从 E 变化时，超过 10% 时电流会发生显着变化 C − 0.2 到 E C − 1.4 eV 并再次饱和超过 20%。这个结果也与图 2 一致。图 11a 和 5。绝对电流密度的等高线图还表明，它在 20% Al 摩尔分数以上饱和，并且直到 10% Al 摩尔分数之前没有显着的电流密度。 图 12。这也验证了在 10% Al 之前未形成 2DEG摩尔分数。在摩尔分数的 20% 以上观察到大量的电子密度，图 13a。沿通道的电场分布绘制在图 13b 中。图 13b 表明，直到 10% 的 Al 摩尔分数和高于 20% 的 Al 摩尔分数时，栅极下方的电场没有显着改善，电场没有太大差异，这限制了较高 Al 百分比下的电流。

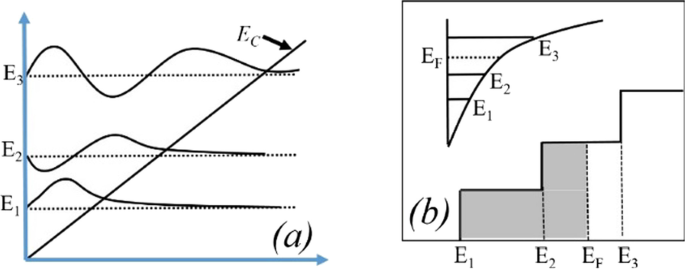
一 Fang–Howard Airy 的三角形势能很好地描绘了子带的能量 波函数。 b 只有较低能量的子带 (E 1 和 E 2、低于费米能级）被占用[28]

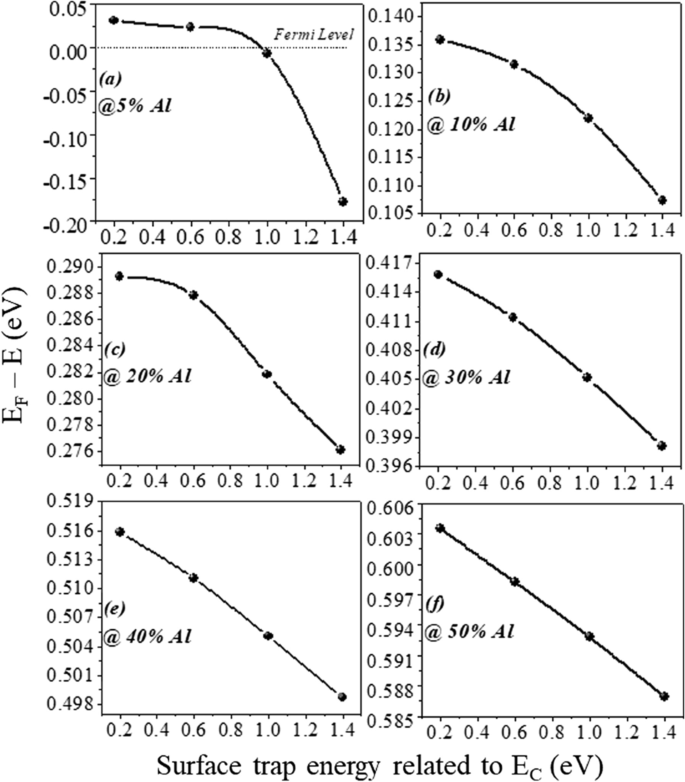
一 –f (E F − E ) 所有铝浓度下表面施主能的变化

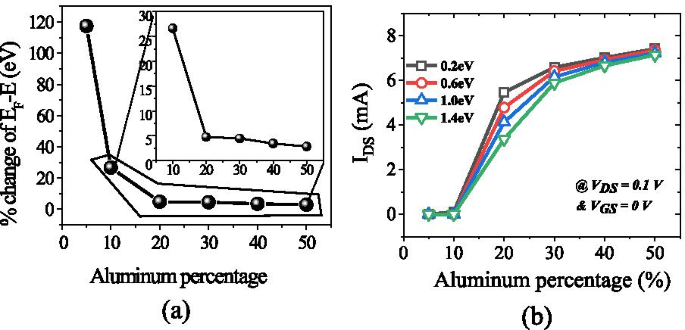
一 能量变化百分比E 当表面供体能量由深到浅变化时，铝浓度随铝浓度变化。 b 漏极电流和 V DS =0.1 V 和 V GS =0 V 在不同的表面供体捕获能量。高达 10% 的器件未观察到显着电流

V 下 0.6 eV 表面供体能量的绝对总电流密度等值线图 DS =0.1 V 和 V GS =0 V

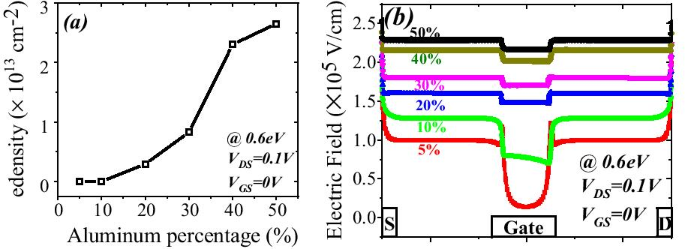
一 电子密度随铝百分比和b的变化 不同铝含量下栅极下方和栅极两侧的电场变化

Conclusion

In this paper, we comprehensively present the effect of surface donor traps along with aluminum percentage on electron density and quantum potential well. This manuscript demonstrated that the percentage change happens in 2DEG and notch below the Fermi level gets saturated above 20% of aluminum concentration when surface donor trap energy goes deep to shallow. The electron density in the two-dimensional quantum potential well is saturated approximately at 8%, whereas the energy below the Fermi level saturates somewhere around 2%. These two results are also in tune with each other, except 5% aluminum, having a condition for not forming two-dimensional well for relatively deep (> 0.9 eV) surface donors. Aluminum percentage above 10% forms two-dimensional quantum potential well even for deeper surface donor traps. The effect of surface donor traps on the surface potential also has been discussed in this work. The results of this paper may provide the impetus to the experimental result validation.

数据和材料的可用性

All data are available on request.

缩写

GaN:

Gallium nitride

HEMT:

High-electron-mobility transistor

2DEG:

Two-dimensional electron gas

DD:

Drift and diffusion transport model

SRH:

Shockley–Read–Hall recombination model