单层 InSe 中电场控制的间接-直接-间接带隙跃迁

介绍

自从单层石墨（即石墨烯）[1, 2] 的实验实现的开创性工作以来，原子级薄的二维 (2D) 材料受到了很多关注 [3, 4]。各种单层二维材料已被理论预测或实验发现，包括硅烯 [5-7]、锗烷 [8]、黑磷 [9, 10]、过渡金属二硫属元素化物 (TMD) [11-13] 和六方氮化硼 [14] –16]。尽管这些原子级薄的二维材料具有相似的蜂窝晶格结构，但它们的电子结构和导电性能却大不相同，包括金属 [1, 2, 5-8]、半导体 [9-13] 和绝缘体 [14-16]。因此，根据它们的电子特性，这些单层二维材料可能会在多功能电子和光学器件的设计中得到应用 [3, 4]。例如，提出了基于 Si-石墨烯超材料 [17]、Cu-石墨烯超材料 [18] 和 MoS2-SiO2-Si 波导结构 [19] 的具有高质量因子的可调光学器件。提出了基于铁磁石墨烯 [20]、具有 Rashba 自旋轨道耦合和磁势垒的应变石墨烯 [21] 以及具有电场的应变硅烯 [22、23] 的完美谷或/和自旋极化装置。此外，SF6 的分解组分与不同材料（包括 N 掺杂的单壁碳纳米管 [24]、Pt3-TiO2(1 0 1) 表面 [25]、Ni 掺杂的 MoS2 单层 [26] 和利用密度泛函理论(DFT)研究了Pd(1 1 1)表面[27]。

III-VI 族化合物 MXs（M =Ga、In 和 X =S、Se、Te）是另一类层状二维材料。由于其独特的电气特性，这些材料引起了许多研究人员的关注 [28]。 DFT [29-33] 和紧束缚模型 [34] 计算表明，层状 MX 的能带隙取决于厚度，随着层数的减少，从 1.3 eV 增加到 3.0 eV。同时，观察到直接-间接带隙跃迁，这与层状黑磷 [9, 10] 和 TMDs [11-13] 的行为相反。分层 MX 的这种相当大的能带隙调制可用于设计光电器件 [35, 36]。此外，研究了掺杂有氧缺陷的 InSe 的稳定性，发现它在空气中比黑磷更稳定 [37]。 InSe 单层的磁性可以通过吸附 As [38]、C 和 F [39] 来调节。由于破坏了镜像对称性，在双层 InSe 中发现了巨大的自旋电荷转换效应 [40]。此外，单层 InSe 纳米带的电子结构和电流-电压特性在很大程度上取决于边缘状态 [41]。另一方面，实验研究验证了 MX 的层相关电子结构，它们可以响应跨越可见光和近红外区域的光 [42-45]。此外，发现 MX 的载流子迁移率很高，使其可用于设计场效应晶体管。对于块体 GaS 和 GaSe，载流子迁移率约为 80 和 215 cm ² V ⁻¹ S ⁻¹ [46]，分别。对于单层 InSe，载流子迁移率甚至高达近 10 ³ 厘米 ² V ⁻¹ S ⁻¹ [47]。此外，层状InSe的带隙可以通过单轴拉伸应变来控制，这可以通过光致发光光谱进行识别[48]。

从光电器件设计的角度来看，基于直接带隙半导体的器件的效率优于基于间接带隙半导体的器件。因此，将间接带隙少层 MX 转化为直接带隙类型对科学界来说是一个挑战。最近，通过单轴应变在单层 InSe 中发现了带隙操纵和间接-直接带隙跃迁 [49]。此外，直接带隙半导体已通过堆叠 2D n-InSe 和 p-GeSe(SnS) 获得。并且这些范德华异质结的带隙值和带偏移可以通过层间耦合和外部电场进行调整 [50]。此外，研究了双层 InSe 可能的堆叠配置以及垂直电场对其电子结构的影响。间接带隙双层 InSe 可以通过改变电场强度而转变为金属类型 [51]。类似地，在其他屈曲二维材料中，如硅烯 [52]、锗烯 [53]、过渡金属二硫属化物 [54, 55] 和黑磷 [56]，也提出了垂直电场来调整其带隙和电子特性。鉴于这些先前的研究，一个自然的问题可能会被问到电场对单层 InSe 电子结构的影响。

在这封信中，通过使用紧束缚模型哈密顿量研究了垂直电场对单层 InSe 电子结构的影响。随着电场强度的增加，可以在所考虑的系统中实现间接-直接-间接带隙跃迁。同时，单层 InSe 的带隙逐渐减小，最终呈现金属性。通过分析能带的轨道分解和能带边缘的电场调制能量位置偏移，揭示了这些效应的潜在物理机制。我们的研究可能有助于从根本上理解少层InSe的电子特性，并为二维光电器件提供理论基础。

方法

InSe 单层的俯视图如图 1a 所示，其中紫色的大球代表铟离子，而绿色的小球代表硒离子。这两种离子在xy中形成类似石墨烯的六方结构 晶格常数 a 的平面 ，最近的 In 或 Se 离子之间的距离。图 1b 显示了 InSe 单层的侧视图示意图。与石墨烯不同的是，在xz中有两个镜像对称的亚层 平面被观察到。不同亚层的 In (Se) 离子之间的垂直距离设置为 d (D ）。因此，单层 InSe 的晶胞由四个离子 S 组成 e 1、我 n 1、S e 2、我 n 2，如图1b中红色椭圆所示，其中数字1(2)表示子层索引。

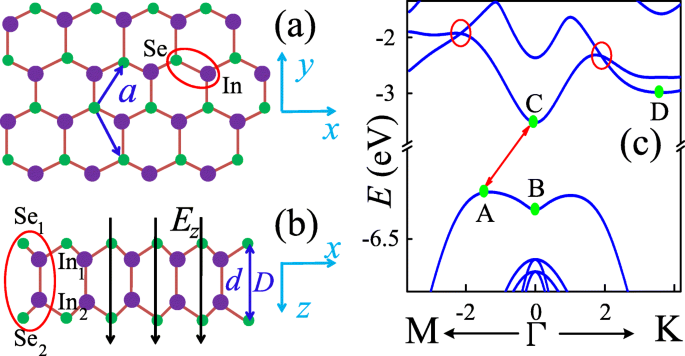
(颜色在线) 顶部 (a ) 和边 (b ) xy 中单层 InSe 的视图 和 xz 分别是飞机。 xy 中最近的 In 或 Se 离子之间的晶格常数 平面是a , 并且不同亚层中最近的 In (Se) 离子之间的距离为 d (D ）。沿 z 的垂直电场 -axis E z 应用于单层 InSe。 c 单层InSe的能带

紧束缚哈密顿量直到第二近邻相互作用，包括 s 之间所有可能的跳跃 和 p In 和 Se 离子的轨道读数 [34]

其中总和在子层 l 上运行 =1 和 2，以及 l ^′ =2(1) 作为 l =1(2)。 H 0l , H 会 , 和 \(\phantom {\dot {i}\!}H_{ll^{\prime }}\) 分别由来自现场能量、两个子层内部和之间的跳跃能量的项组成。并且它们的显式表达式为[34]

其中总和在子层 l 中的所有单元格上运行 . \(\phantom {\dot {i}\!}\varepsilon _{\mathrm {In(Se)}_{s}}\) 是 s 的现场能量 In (Se) 离子的轨道，而 \(\phantom {\dot {i}\!}\varepsilon _{\mathrm {In(Se)}_{p_{\alpha }}}\) 是轨道 p α (α =x ,y ,z ）。 \(a_{lis}^{\dag }\) (a lis ) 是 s 中电子的创造（湮灭）算子 在晶胞 i 中 In 离子的轨道 和子层 l , 但是 \(\phantom {\dot {i}\!}a_{{lip}_{\alpha }}^{\dag }\) (\(\phantom {\dot {i}\!}a_{{ lip}_{\alpha }}\)) 对于 p 中的电子 α 轨道。类似地，b ^† (b ) 是 Se 离子相关轨道中电子的创造（湮灭）算子。

其中 [34]

和

包括同一子层内最近邻 In-Se、In-In、Se-Se 和次最近 In-Se 对之间的跳跃项 l ， 分别。 \(T_{ss/sp/ps}^{\mathrm {X}}\) 是 ss 的跳跃积分 /sp /ps 对应对 X 之间的轨道，而 \(T_{\pi (\sigma)}^{\mathrm {X}}\) 是平行 p 的轨道 和 p 轨道垂直于（沿着）跳跃向量 \(R_{\alpha }^{\mathrm {X}}\) [57]。例如

其中 \(\phantom {\dot {i}\!}\mathrm {\mathbf {R}}_{{\text {In}_{li}}/{\text {Se}_{lj}}}\ ) 是 Inli 的位置向量 /Selj , \(\hat {\mathbf {\alpha }}\) 是沿 α 的单位向量 .

其中 [34]

和

包括子层之间最近邻 In-In、In-Se 和下一个最近 In-In 对之间的跳跃项 l 和 l ^′ ， 分别。如果沿 z 的垂直电场 -axis 应用于单层 InSe，它的影响可以通过改变 In 和 Se 离子的现场轨道能量来引入，即

其中 e 是电子电荷和 E z 是垂直电场的强度。可以通过向单层 InSe 添加顶栅和底栅来实现垂直电场。此外，在单层 InSe 和栅极之间插入两个绝缘层以消除沿 z 的电流 -轴。因此，可以通过改变门控电压来调节电场强度。

通过转换等式中的紧束缚哈密顿量。 (1) 进入k 空间，然后将其对角化，能带 E (k ) 的单层 InSe 没有或有垂直电场可以方便地获得，其中 k 是波矢量。同时，特征向量系数C n k (o ) 在波段 n , 轨道 o , 和波矢量 k 也可以实现。

数值结果和讨论

图 1a 和 b 中单层 InSe 的晶格参数取为 a =3.953 Å, d =2.741 Å 和 D =5.298 Å，这是通过局部密度近似获得的 [30]。紧束缚哈密顿方程中的现场能量和跳跃能量。 (1) 在表 1 中给出，由密度泛函理论数据拟合，并进行剪刀校正 [34]。虽然这里只给出了单层 InSe 的数值结果，但在双层 InSe 和块状 InSe 中也发现了定性相似的结果。为简洁起见，这封信中未列出这些内容。

图 1c 显示了单层 InSe 的能带。 Γ点周围的导带显示出类似抛物线的能量色散，这与其他普通半导体的导带相似。然而，沿 Γ−K 的能带结构与沿 Γ−M 的能带结构略微不对称。最低的两个导带沿这两个方向相互交叉，如红色循环所示。与导带相反，最高价带是平坦的，但在 Γ 点附近略微倒置，形成了有趣的墨西哥帽状结构。因此，单层 InSe 是一种间接带隙半导体，这与块状 InSe 有很大不同，因为它是直接带隙半导体。单层 InSe 的能隙可由下式得到 \(E_{\mathrm {g}}^{\text {id}}=E_{\mathrm {C}}-E_{\mathrm {A}}=2.715\) eV，与块体 InSe \(E_{\mathrm {g}}^{\mathrm {d}}=1.27\) eV [34] 相比，eV 放大了很多。而其他价带则表现出正常的抛物线状能量色散。

为了理解图1c所示的单层InSe的能带，轨道分解|C n k (o )| ² 能带如图 2 所示。由于单层 InSe 的两个亚层沿 z 对称 轴，不同亚层中的离子对能带具有相同的轨道贡献。这里，以子层 2 中的 In 和 Se 离子为例，如图 1b 所示。上图表示 In 离子的轨道贡献，而下图表示 Se 离子的轨道贡献。线条的粗细与归一化的轨道贡献成正比。可以看出，Γ点附近的最低导带首先来自p z Se 离子的轨道，然后是 s In 离子的轨道。 K点附近的第二导带主要来源于p x In 离子的轨道，然后 p z Se 离子的轨道。然而，最高价带主要来自 p z Se 离子的轨道。其他价带来自 p x 和 p 是 Se 离子的轨道。这些结果与DFT计算得到的结果一致[34]。

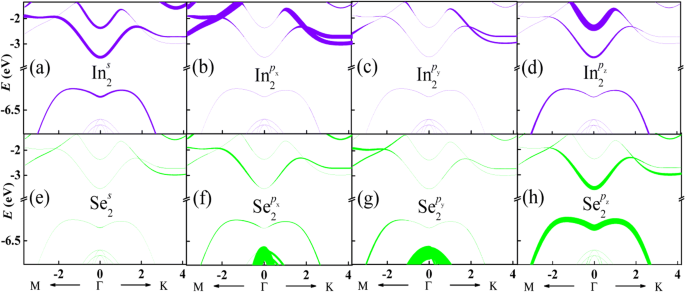
（在线颜色）单层 InSe 能带的轨道分解。较粗的线表示更大的贡献。由于单层 InSe 的两个亚层沿 z 具有镜像对称性，因此仅选择亚层 2 中的 In 和 Se 离子作为示例 -轴 (a –h )

具有沿 z 的垂直电场的单层 InSe 的能带 -轴如图 3a 所示。电场强度取为E z =2.0V/nm。通过与图 1c 中的能带进行比较，每个导带和价带作为一个整体被提升到更高的能量区域。然而，每个能带的能量位移是不同的，因为它从 p 的轨道分解 z In 和 Se 离子的轨道不同。最高价带最大值的位置改变到Γ点，而导带最小值的位置保持不变。因此，单层 InSe 转变为直接带隙半导体。并且能隙减小到 \(E_{\mathrm {g}}^{\mathrm {d}}=2.61\) eV。此外，沿 Γ-K 和 Γ-M 方向的交叉点被打开，从而产生能隙，如红色循环所示，因为沿 z 的对称性 -轴被垂直电场破坏。当电场强度增加到E z =6.0 V/nm，Γ 点的能隙减小，但交叉处的能隙进一步增加，如图 3b 所示。有趣的是，导带最小值的位置从Γ点改变到了K点附近，而最高价带的最大值则停留在Γ点。这种现象意味着单层InSe再次转变为间接带隙半导体，整个带的间接能隙\(E_{\mathrm {g}}^{\text {id}}=1.30\) eV。同样，单层 InSe 的带隙可以通过双轴应变来控制。当应变从 1% 到 4% 变化时，带隙范围从 1.466 到 1.040 eV。此外，当单层 InSe 处于单轴应变下时，也观察到间接-直接带隙跃迁 [49]。对于具有垂直电场的双层 InSe，其带隙随着电场强度的增加而减小，当电场强度增加到 2.9 V/nm 时会关闭[51]。

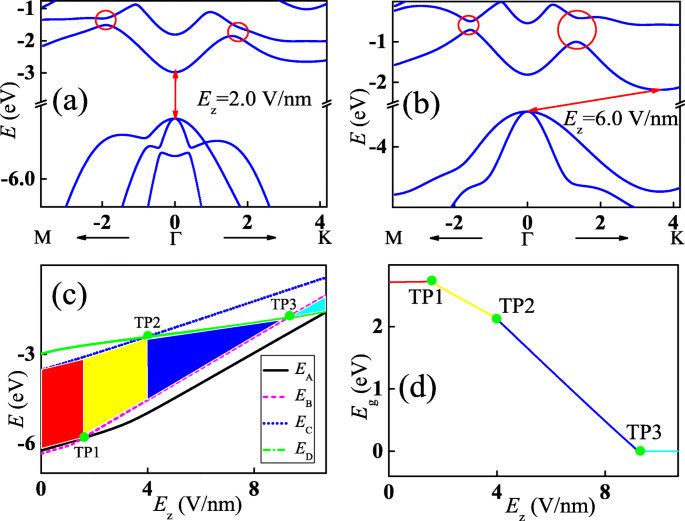
(Color online) 不同强度的垂直电场调制单层 InSe 的能带 E z =2.0 V/nm(a ) 和 6.0 V/nm (b ）， 分别。 a 中的红色圆圈 和 b 表示图 1c 所示交叉点周围的开放能隙。 c 图 1c 中显示的点 A（黑色实线）、B（品红色虚线）、C（蓝色虚线）和 D（绿色虚线）处的能量作为电场强度的函数. d 作为电场强度的函数的全局带隙。黄线表示直接带隙，红蓝线表示间接带隙

为了更清楚地理解在垂直电场存在下单层InSe电子结构的变化过程，图1c所示的带边缘处A、B、C、D点对应的波矢量处的能量。作为电场强度的函数如图 3c 所示。随着电场强度的增加，所有这些点的能量都向上移动，证实了图 3a 和 b 中能带的演变。当电场强度E z <1.6 V/nm，价带中A点的能量高于B点，而导带底位于C点。因此，该强度范围内的电场调制单层InSe是间接带隙半导体，如红色区域所示。然而，A点和B点的能量将在TP1交叉，然后随着电场强度的进一步增加，B点的能量将高于A点的能量。同时，导带底部保持不变，直到电场强度增加到 4.0 V/nm。因此，该强度范围内的电场调制单层 InSe 是直接带隙半导体，如黄色区域所示。与价带中 A 点和 B 点之间的能量交叉类似，在导带中 C 点和 D 点的能量中也观察到传输点，如 TP2 所示。如果电场强度小于 9.23 V/nm，D 点的能量低于 C 点，而价带顶部仍停留在 B 点。因此，电场调制的单层 InSe 再次变成间接带隙半导体，如蓝色区域所示。有趣的是，最高价带中的 B 点和最低导带中的 D 点的能量也会在 TP3 处交叉，这意味着能带隙是闭合的。此外，当电场强度大于 9.23 V/nm 时，B 点的能量将高于 D 点的能量。因此，最低导带和最高价带将重叠，使得电场调制的单层 InSe 在这种情况下变成金属，如青色区域所示。对应于图 3c 中不同颜色区域的全局带隙绘制在图 3d 中。与红色区域对应的带隙几乎与变化的电场强度无关，如红线所示。然而，黄色区域的带隙随着电场强度的增加而线性减小。在蓝色区域也发现了类似的带隙行为，但斜率更大。只要电场强度大于点TP3处的电场强度，带隙就会减小到零，如青色线所示。电场调制带隙行为表明层状 III-VI 半导体在设计新型光学探测器和吸收器方面具有潜在的应用。此外，这些器件的光谱响应频率从紫光 (ν ≈6.57×10 ¹⁴ 赫兹为 E z =1.6 V/nm) 到红外光 (ν <3.97×10 ¹⁴ 赫兹为 E z>5.18 V/nm）。

众所周知，材料的电子特性主要由能带边缘决定。根据图 2 中能带的轨道分解，单层 InSe 的导带和价带边缘主要来自 p z Se 离子的轨道。因此，只有 p z 对于图 3a 和 b 所示的能带，子层 2 中 Se 离子的轨道分解分别显示在图 4a 和 b 中。通过与图 2h 的比较，p z 对导带的轨道贡献略有改变。因此，这些带结构的形状几乎没有受到影响。然而，p z 对价带的轨道贡献被强烈修改，导致这些带结构的形状发生变化。此外，根据 p z 具有垂直电场的单层 InSe 能带的轨道分解，每个导带的相对位置保持不变，尽管间隙在带交叉处打开，如红色循环所示。相反，每个价带的相对位置发生变化。 Γ 附近低价带的能量 点增加并最终超过最高价带的点，导致间接-直接带隙跃迁。

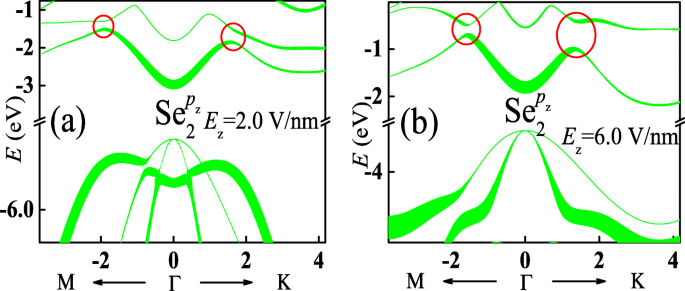
（颜色在线）a 和 b 显示 p z 图 3a 和 b 中分别显示了具有垂直电场的单层 InSe 能带的亚层 2 中 Se 离子的轨道分解。粗线代表更重要的贡献

结论

研究了在垂直电场调制下单层 InSe 的电子结构。通过调节电场强度，发现单层 InSe 的间接-直接-间接带隙跃迁。同时，该系统的全局带隙随着电场强度的增加而单调减小到零，这意味着实现了半导体-金属转变。通过分析能带边缘的能量变化和能带的轨道分解，阐明了在垂直电场存在下单层InSe能带的演化。这些结果可能有助于进一步了解单层InSe的电子结构，以及设计响应从紫光到远红外光的单层InSe基光电器件。

数据和材料的可用性

本文包含支持本文结论的数据集。

缩写

二维：

二维

DFT：

密度泛函理论

TMD：

过渡金属二硫属化物