石墨烯中具有 Y 形凯库勒晶格畸变的电控谷赝磁电阻

介绍

石墨烯是一种二维碳原子片，具有优异的载流子迁移率，并提供最薄的通道，可用于设计金属氧化物半导体场效应晶体管 [1]。 Semenov 提出了一种利用石墨烯层作为通道的自旋场效应晶体管[2]，涉及铁磁源漏自旋注入和自旋检测，通道中的自旋操纵是通过电子交换的电控制来实现的。与铁磁门相互作用。此外，Rashba 自旋轨道相互作用是另一种有前途的石墨烯自旋控制工具 [3]。 Rashba 自旋轨道相互作用可以引起自旋进动，从而控制通道电子的自旋方向。自旋场效应晶体管还激发了许多重要的研究思路，如巨磁电阻和隧道磁电阻 [3, 4]。巨磁阻和隧道磁阻可应用于数字存储和磁传感器技术。

另一方面，除了传统的电荷和自旋对应物之外，石墨烯中的狄拉克电子还具有额外的谷自由度。由于两个谷之间的大动量差异和清洁石墨烯样品中间隔散射的抑制[5-7]，谷自由度被认为在携带和操纵信息方面发挥与电子自旋相同的作用，即导致作为谷电子学兴起的一门新学科。与自旋场效应晶体管类似，在石墨烯中理论上也提出了谷场效应晶体管[8]，它由夹在两个扶手椅石墨烯纳米带（源极和漏极）之间的带隙石墨烯的量子一维通道组成；然后，将侧栅电场施加到沟道并由于谷-轨道相互作用而调制载流子的谷极化，从而控制在漏极收集的电流量。然而，由于石墨烯中的谷耦合很久没有成为物理现实，基于石墨烯谷场效应晶体管的进一步研究和相关研究很少。 Gutierrez 等人最近的实验。 [9] 在石墨烯-铜超晶格上的蜂窝晶格中揭示了一种不寻常的 Y 形 Kekulé(Kek-Y) 键结构，其中每个超晶格晶胞中的六个碳原子中的一个在其下方没有铜原子并获得更短的最近邻债券。此外，Gamayun 已经表明，Kek-Y 键结构为动量控制的谷进动提供了一种方法 [10]。比纳克等人。 [11] 表明 Kek 系统可以通过类 Andreev 反射产生山谷翻转效应。最近王等人。 [12] 发现保持系统反转对称性的 Kekulé 晶格的 C-C 键长调制可用于以类似于交换场进动自旋的方式操纵谷自由度。这使得在石墨烯中设计一种新型谷场效应晶体管成为可能。此外，没有关于 Kek-Y 晶格畸变对石墨烯谷赝磁电阻的综合影响的报道。谷赝磁阻 [13, 14] 类似于磁隧道结中的磁阻 [15]，其中自旋电流的大小取决于电极的磁取向 [4]。

方法

在这项工作中，我们提出了一种用于石墨烯基电子的新型谷场效应晶体管 (VFET)。该器件设计假设有一个铁磁应变 (FM-S) 源极/漏极用于谷极化注入/检测，类似于传统的自旋晶体管（见图 1a）。石墨烯通道中的谷旋转依赖于 Kek-Y 石墨烯超晶格 [10-12]，这可以通过外延生长在 Cu(111) 上的石墨烯超晶格实现，铜原子与碳原子对齐 [9]。然而，一些碳原子下方缺少铜原子，导致石墨烯下方出现一些周期性的铜原子空位。这种衬底原子空位导致三个相邻的键收缩。这里，我们使用 δ t 表示对应于这三个键的电子跳跃的能量修改。我们假设铁磁石墨烯由相同的 FM 金属条制成。源极和漏极的两个磁化沿电流方向（x 轴），它可以在平行（P）或反平行（AP）对齐，在外部平面磁场的帮助下。在朗道规范中，由边缘场产生的磁矢量势的形式为 [16, 17] \(A(r)=A_{y}(x)\overrightarrow {y}\) with A 是 (x )=A 是 [Θ (-x )±Θ (x -L )]，其中加（减）号对应于磁化强度的 P(AP) 配置，Θ (x ) 是 Heaviside 阶跃函数。另一方面，我们假设在 VFET 的源极和漏极上施加相同的应变，这可以由石墨烯衬底上的张力引起 [18]。弹性变形可以被视为对跳跃幅度的扰动，并作为规范势A S (r ）。张力沿 x 设置 方向，在这种情况下，A S (r ) 沿 y 均匀 轴 [16]。为了确定性，我们取其 y 的典型平滑轮廓 组件作为 A Sy (x )=A S [Θ (-x )+Θ (x -L )]，其中 A S 是振幅。此外，Kek-Y晶格区还施加了一个电势垒，可以通过外部偏置电压进行调节。

<图片>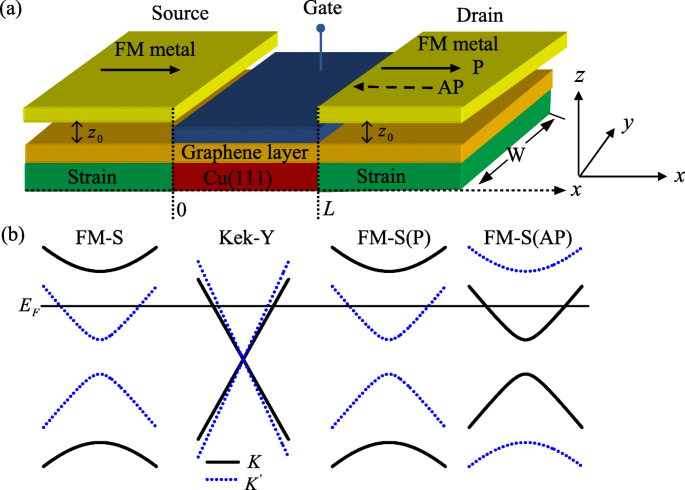

一 利用具有 Kek-Y 晶格畸变和栅极偏置的石墨烯通道的 VFET 示意图，该通道控制通道电子的谷取向。源极和漏极是 FM-S 石墨烯，它们以特定的极化注入和检测电子。其中 z 0 是石墨烯层和 FM 条纹之间的距离。 L 是通道长度，W 是 y 中石墨烯样品的宽度 方向，和 W ≫L . b 狄拉克点附近的能带结构。横线表示费米能量（颜色在线）

低能激发准粒子在具有 Kek-Y 石墨烯超晶格的 VFET 中的传播可以用以下单粒子哈密顿量来描述 [10-12]

$$ \begin{array} [c]{ll} H=&v_{F}(\mathbf{P}\cdot\sigma)+v_{\tau}(\mathbf{P}\cdot\tau)\Theta \left(x\right) \Theta\left(Lx\right) +\\ &U\sigma_{0}\tau_{0}\Theta\left(x\right) \Theta\left(Lx\right) + A_{M}(x)\sigma_{y}+\tau_{z}A_{S}(x)\sigma_{y}。 \end{数组} $$ (1)

这里，σ 和 τ 分别是亚晶格和谷的泡利矩阵。 P =(p x ,p 是 ) 是无质量狄拉克电子的动量，τ z K =±1 和 \(K^{^{\prime }}\) 山谷，v F =10 ⁶ m/s 是原始石墨烯中狄拉克电子的速度，v τ ≃v F δ t /3t 是 Kek-Y 晶格中键收缩效应的速度修正项 [12]，其中 t 是原始石墨烯的最近相邻引用之间的跳跃能量。 U 是栅极可调势垒。 A M (x )=e v F A 是 (x ) [19]。具有Kek-Y晶格畸变和电势垒的石墨烯中哈密顿量的特征值由下式给出

$$ E_{\alpha,\beta}=U+\alpha(\hbar v_{F}+\beta\hbar v_{\tau})\sqrt{k_{x\beta} ^{2}+k_{y} ^{2}}。 $$ (2)

这里，α =+1(-1) 指定导（价）带。 β =±1 表示导带和价带的两个谷裂子带。由于 y 中的平移不变性 方向，横波矢量k 是 是守恒的。具有均匀 Kek-Y 晶格畸变的石墨烯中的本征态特征为 \(\Psi _{\beta }^{\pm }(k_{x\beta },k_{y})=\frac {1}{ N_{\beta }}\left (1,P_{\beta }^{\pm },Q_{\beta } ^{\pm },R_{\beta }^{\pm }\right)^{T} \)，其中 N β 是归一化常数 \(N_{\beta }=\left (1+P_{\beta }^{2}+Q_{\beta }^{2}+R_{\beta }^{2}\right)^ {\frac {1}{2}}\) 和 \(P_{\beta }^{\pm }, Q_{\beta }^{\pm }\) 和 \(R_{\beta }^{\ pm }\) 是定义如下的函数：

$$ \begin{array} [c]{cc} P_{\beta}^{\pm}=&\frac{(EU)^{2}+\left(\hbar^{2}v_{F}^ {2}-\hbar^{2}v_{\tau} ^{2}\right)\left(k_{x\beta}^{2}+k_{y}^{2}\right)}{2 (EU)\hbar v_{F}(\pm k_{x\beta}-{ik}_{y})},\\ Q_{\beta}^{\pm}=&\frac{(EU)^ {2}-\left(\hbar^{2}v_{F}^{2}-\hbar^{2}v_{\tau} ^{2}\right)\left(k_{x\beta}^ {2}+k_{y}^{2}\right)}{2(EU)\hbar v_{\tau}(\pm k_{x\beta}-{ik}_{y})},\\ R_{\beta}^{\pm}=&\frac{(EU)^{2}-\left(\hbar^{2}v_{F}^{2}+\hbar^{2}v_{\ tau} ^{2}\right)\left(k_{x\beta}^{2}+k_{y}^{2}\right)}{2\hbar^{2}v_{F}v_{\ tau}(\pm k_{x\beta} -{ik}_{y})^{2}}。 \end{array} $$ (3)

从\(K^{^{\prime }}\)谷到\(K(K^{^{\prime }})\)谷的传输概率\(T_{K^{^{\prime }}, K(K^{^{\prime }})}\) 可以使用传递矩阵技术 [20] 来计算。根据 Laudauer-Btittiker 公式，依赖于谷的电导由 [21] 给出：

$$ G_{K^{^{\prime}},K(K^{^{\prime}})}=G_{0} {\int_{-\frac{\pi}{2}}^{\ frac{\pi}{2}}} T_{K^{^{\prime}},K(K^{^{\prime}})}\cos(\phi_{0})d\phi_{0} . $$ (4)

这里 \(G_{0}=2e^{2}W/\left (v_{F}\pi ^{2}\hbar ^{2}\right)\left \vert E\right \vert \), <我>W 是 y 中石墨烯样品的宽度 方向和 ϕ 0 是相对于 x 的入射角 方向。

在进行计算之前，我们用 k 讨论能带结构 是 =0，如图1b所示。在FM-S源区，石墨烯的能带写为\(E=\alpha \sqrt {(\hbar v_{F}k_{x})^{2} +(A_{M}+\tau _{z}A_{S})^{2}}\)。可以发现谷简并是升力，在K处诱导出不同的间隙 和 \(K^{^{\prime }}\) 点，因为总向量势 A M +A S 作用于 K 电子高于总矢量势|A M -A S |作用于 \(K^{^{\prime }}\) 电子 [19]。这表明当入射能量位于|A时，只有\(K^{^{\prime }}\)电子可以通过FM-S源区 M -A S |<E <A M +A S [22, 23]。同理，在 FM-S 漏区，石墨烯的能带可以写成 \(E=\alpha \sqrt {(\hbar v_{F}k_{x})^{2}+(\pm A_{ M}+\tau _{z}A_{S})^{2}}\)，其中 ± 符号对应于磁化的 P 和 AP 配置。所以只有 \(K^{^{\prime }}\) 电子在 P 结构中被检测到并且只有 K 当费米能量位于 [|A 范围内时，在 AP 结构中检测到电子 M -A S |,A M +A S ]。在石墨烯通道中，谷简并也是升力，但有一个重要的区别。与领先案例相反，其中 K 的阶段 和 \(K^{^{\prime }}\) 分量以相同的波矢[即 \(k=E/\hbar v_{F}\)] 演化，现在，它们分别以不同的波向量演化 ( \(k_{+}=(EU)/(\hbar v_{F}+\hbar v_{\tau })\) 和 \(k_{-}=(EU)/(\hbar v_{F}-\ hbar v_{\tau })\)) 由于 Kek-Y 石墨烯超晶格混合谷（见方程 2）。这导致谷空间中沟道电子的谷进动[12]。石墨烯中的谷进动是谷场效应晶体管的基础[8]。谷进动也可以通过 FM-S/Kek-Y/FM-S 结中的谷赝磁阻 (VPMR) 来表征，类似于基于石墨烯的量子隧道结中的磁阻与自旋轨道相互作用 [4] ，定义为 \(VPMR=\frac {G_{P}-G_{AP}}{G_{P}}\)，其中 G P 和 G AP 分别代表 P 和 AP 配置中的电导，并且 \(G_{P}=G_{K^{^{\prime }},K^{^{\prime }}}, G_{AP}=G_{K ^{^{\prime }},K}\)。谷值电流的大小取决于我们考虑的器件中源极和漏极的磁取向。

数值结果和讨论

在下文中，我们展示了石墨烯中 FM-S/Kek-Y/FM-S 结的数值结果。在整篇论文中，我们设置通道长度 L =207nm，并将费米能量限制在 20 meV<E <140meV，假设满足 |A M -A S |<E <A M +A S .图 2a 和 b 显示了隧道电导和 VPMR 作为 v 的函数的计算结果 t 与费米能量 E =80meV 和矩形势垒 U =-10meV。我们可以发现 G P 和 G AP 具有相同的振荡周期但相反的相位。因此，VPMR随着v的增加而振荡 t 并且可以出现负值 VPMR。这些现象类似于具有自旋轨道相互作用的弹道石墨烯基量子隧道结中的磁阻情况 [4]。 G的电导振荡特性 P 和 G AP 可以通过两个谷分量之间的相位差来解释。当入射角ϕ 0=0，相移由下式给出： \(\Delta \theta =(k_{x+}-k_{x-})L=-\frac {2(EU)v_{\tau }}{\hbar ( v_{F}^{2}-v_{\tau }^{2})}L\)。 Δ θ 确定电子进入漏极之前谷极化的方向，相对于漏极状态[8]。对于Δ θ =±2n π ,n =1,2,3⋯，两个极化对齐，导致电导G P 最大值和 VPMR 为高正值（如 v τ =0.022, 0.033)。另一方面，对于Δ θ =±(2n +1)π ,n =0,1,2⋯，它们相互正交，导致电导G AP 最小值和 VPMR 负值（如 v τ =0.0167, 0.027, 0.038).

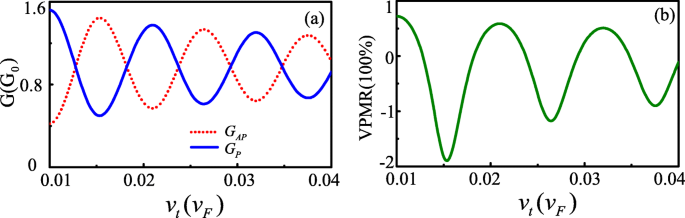
电导G P ,A P 和 VPMR 与 v t 在 L =207nm,E =80meV 和 U =−10meV（彩色在线）

电导和 VPMR 不仅是跳跃能量修改的振荡函数，它们还随费米能量和有效势垒势而振荡，因为 Δ θ 尺度也与费米能量和势垒 U 成线性关系 .图 3a 和 b 分别显示了作为费米能量和有效势垒电位函数的电导。相应的 VPMR 在图 3c 和 d 中给出。它们都表现出随 E 变化的振荡特性 和 U 值，即使当有效势垒U 大于费米能量 E .这种现象的物理起源与克莱因隧道[12]有关。尽管对于增加的 E 存在类似的电导和 VPMR 振荡现象 和 U ，也可以发现一些差异。作为 E 增加，G 之间的差异 P 和 G AP 电导越来越小，导致 VPMR 的振荡幅度随着费米能量的增加而减小。而在Δ条件下 θ =±n π 满足，G的区别 P 和 G AP 随着 U 的增加而增大 ，尤其是在某些位置，G P 和 G AP 电导呈现开关特性。这些字符更适合 VPMR 的应用。值得注意的是，观察到的 VPMR 最大值在小 E 时超过 30,000% .这个值大大超过了~的MR 175% 在基于弹道石墨烯的量子隧道结中具有自旋轨道相互作用 [4] 和 ~ 的赝磁阻 100% 在由外栅控制的双层石墨烯中 [24]，甚至大于 ~ 的 VPMR 10000% 在合并狄拉克锥系统中[13]。

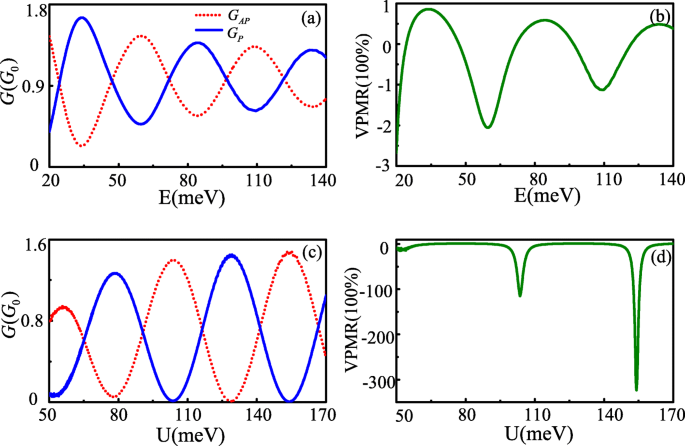
电导G P ,A P (a , c ) 和 VPMR (b , d ) 作为费米能量和 L 的电势垒的函数 =207nm,v t =0.02v f .其他参数是 U a =−10meV 和 c , E b =80meV 和 d （颜色在线）

结论

总之，我们提出了一种用于石墨烯基电子的谷型场效应晶体管，并通过它研究了谷型赝磁电阻。我们已经表明，谷赝磁电阻的振荡特征不仅与跳跃能量修改和费米能量有关，而且可以在很大程度上通过有效势垒电位进行调整。由外部偏置电压调节的谷赝磁电阻有利于谷场效应晶体管器件，我们预计这里提出的电控谷量子器件可以在量子和量子经典混合计算机中发挥作用。

进一步的研究可能涉及不同应变（单轴与双轴）在我们提出的基于石墨烯的谷场效应晶体管中可调电子的谷散射和传输，因为该着色可用于控制 Kekule 模式中的间隔散射程度 [25] .然后，石墨烯中的其他二维材料（MoS2、WS2、WSe2 等）类似物也可以为其他具有 Y 形凯库勒晶格畸变的二维材料基谷场效应晶体管提供一个有趣的平台。

数据和材料的可用性

本文包含支持本文结论的数据集。

缩写

AP：

反平行

FM-S：

铁磁应变

Kek-Y：

Y形凯库勒

P:

平行

VFET：

谷场效应晶体管

VPMR：

谷赝磁电阻