使用基于 AFM 尖端的动态犁式光刻在聚合物薄膜上制造具有高通量的纳米级凹坑

背景

近年来，纳米技术的飞速发展引起了纳米结构在纳米机电系统、纳米传感器和纳米光子学等各个领域的应用越来越多的关注。特别是纳米点，被定义为一维纳米结构，被广泛应用于高密度存储和量子点制备领域[1]。然而，纳米点的有效制造仍然面临着巨大的挑战。许多学者提出了在各种材料上制造纳米点的各种方法。其中，化学合成方法被广泛用于获得纳米点，用于大多数性质检测和纳米级设备[2]。然而，使用这种方法很难确定纳米点的尺寸和空间分布。这导致在后续过程中需要更多的工作来定位和操作。因此，许多学者投入资源探索更可控的方法来获得几纳米尺寸的纳米点结构，例如聚焦离子束光刻[3]、电子束光刻[4]和纳米压印光刻[5]。然而，复杂性、严格的环境要求和/或高成本极大地阻碍了这些技术的应用。

自 1986 年原子力显微镜 (AFM) 发明以来，它已被普遍用作高精度表面轮廓仪 [6]。当 AFM 针尖与样品的相互作用力放大到一个比较大的值时，例如几百纳牛顿甚至几百微牛顿，样品材料就可以被锋利的针尖塑性地去除，类似于一个小刀具[7] ]。化学能和热能也已通过局部氧化 [8] 或加热样品 [9] 引入 AFM 系统，以帮助去除样品材料。因此，它产生了一些新的制造方法，以扩展现有的基于 AFM 尖端的纳米光刻 (TBN) 方法的范围。在所有 TBN 方法中，机械去除方法是最简单和最灵活的 [10]。该方法首先包括对各种材料的压痕和随后的刮擦动作，其中尖端与材料的相互作用强烈依赖于材料的类型，例如金属 [11]、半导体 [12、13] 和聚合物 [14]。通过在纳米尺度上精确控制尖端与材料的相互作用，已成功制造出复杂且高精度的纳米结构，例如纳米点、纳米凹槽，甚至 3D 纳米结构。特别是有学者在半导体材料表面进行了基于AFM尖端的纳米压痕工艺，以获得纳米点结构[15, 16]。在他们的研究中，由纳米压痕引起的晶体缺陷已被确定为 InAs 纳米结构的成核位点。然而，半导体材料相对较大的硬度会导致严重的尖端磨损。因此，一些研究人员提出在较软的材料（例如聚合物薄膜抗蚀剂）上进行纳米压痕工艺，以首先制造纳米点结构。然后可以通过反应离子蚀刻 (RIE) 或湿法蚀刻工艺将这些纳米点结构转移到半导体材料上 [17]。由于其低硬度和超薄厚度，抗蚀剂层可以用相对较小的法向载荷穿透。一些学者提出了在聚碳酸酯表面获得纳米点阵列的两步划痕方法[18]。这种方法依赖于由基于 AFM 尖端的力恒定刮擦过程形成的材料的波纹。然而，相邻纳米点之间的间距仅取决于AFM尖端的几何形状，纳米点的形成机制尚不清楚。

另一方面，低通量是阻碍基于 AFM 尖端的纳米制造方法发展的关键因素。已经证明，基于 AFM 尖端的纳米压痕过程对于获得大规模纳米点结构非常耗时 [19]。为了解决这个问题，Vettiger 等人。提出了“千足虫”的概念，它采用并行操作的大型微悬臂阵列来实现超高密度加工能力[20]。考虑到大面积刮擦过程后尖端磨损严重，一些学者提出了一种新颖的间歇接触模式操作，以减少尖端-样品相互作用力，从而减少尖端磨损 [21, 22]。然而，这种方法使用的大阵列微悬臂需要复杂的设计和生产过程，并且需要一个繁琐的过程来调整一个探针上所有尖端的位置以保证与样品的接触。因此，一些研究人员修改了商用 AFM 系统，包括硬件和软件，以提升高速加工能力 [23,24,25]。在这些方法中，使用了一个悬臂的吸头。然而，使用这些方法只能有效地制造纳米凹槽，并且高速划伤也可能导致严重的尖端磨损。除了使用 AFM 针尖进行静态处理外，基于 AFM 针尖的动态犁式光刻 (DPL) 近来也受到越来越多的关注；这个过程是在原子力显微镜系统的敲击模式下进行的。当增加悬臂的驱动幅度时，AFM 尖端可以穿透样品表面以实现加工过程 [26,27,28]。由于 DPL 方法中尖端和样品之间的间歇接触，可以减少尖端磨损，类似于参考文献中提出的方法。 [21, 22]。通过DPL方法获得的加工深度通常在几个纳米的数量级，适用于在薄膜上制造纳米结构，如聚合物薄膜抗蚀剂和二维材料[29]。此外，在 DPL 方法中，AFM 尖端的悬臂可能会被驱动以数千赫兹的频率振荡，这将导致尖端在短时间内与样品表面多次相互作用。因此，DPL方法可能是一种在薄膜样品表面高效制备纳米级凹坑结构的潜在方法。

在这项研究中，提出了一种基于 DPL 制造方法并采用商业 AFM 系统的快速扫描纳米光刻 (FSN) 方法。图 1a 显示了使用类金刚石碳涂层尖端的纳米划痕过程的示意图，它说明了尖端与硅基板上的聚（甲基丙烯酸甲酯）（PMMA）薄膜接触的视图。悬臂在其共振频率附近被驱动，以在尖端和样品表面之间产生间歇性接触。尖端的驱动幅度由控制系统 (AM-AFM) 维持在一个恒定值。 AFM系统配备的Nanoman模块用于所有加工过程，划痕方向选择为与悬臂长轴平行。研究了划痕速度对加工纳米结构的影响。此外，还研究了凹坑结构的形成机制。

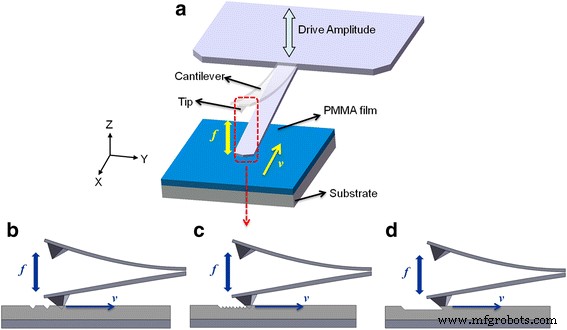
一 使用 FSN 方​​法在 PMMA 薄膜表面上划线过程的示意图。悬臂以其共振频率f振动 在垂直方向。刮擦速度v 沿快速扫描方向修改。描绘了各种刮擦速度范围：b 高刮擦速度，c 中等刮擦速度，d 低刮擦速度

方法

PMMA 溶液的浓度为 1.25 wt%，通过将分子量 Mw =120,000 的 PMMA 粉末溶解在氯苯中制备。 PMMA 薄膜是通过在一块单晶硅衬底上旋转溶液来制备的，该衬底通过在丙酮和酒精中连续超声浴清洗大约 10 分钟。在实验中选择旋转速度为 6000 rpm 以生成厚度为几十纳米的薄膜。在涂覆过程之后，将 PMMA 薄膜在 125°C（接近 PMMA 的玻璃化转变温度）下烘烤 30 分钟。

实验使用商业 AFM (Dimension Icon; Bruker Corporation, USA) 进行。选择具有 42 N/m 标称弹簧常数和 320 kHz 谐振频率的硅尖端，由制造商（TESPD；Bruker Corporation，USA）提供。悬臂的尖端侧用类金刚石碳 (DLC) 涂层硬化，以延长尖端寿命。 PMMA 表面上的纳米结构的测量设置为轻敲模式，扫描速率为 1 Hz，扫描线为 256。当使用不同的探针时，必须调整悬臂系统。在这项研究中，设置点被调整到 300 mV 左右。使用Bruker公司提供的Nanoscope Analysis软件对图像进行一阶展平处理。

在本研究中，AFM 系统中配备的 Nanoman 模块用于划痕过程，该模块被广泛用于设计尖端的轨迹，以在样品表面实现理想的结构，如矩形或圆形。要修改表面，尖端的驱动幅度值应增加到 V w（书写），其中促进尖端和 PMMA 膜之间的相互作用以保证尖端穿透样品表面。划痕过程后，尖端的驱动幅度值立即下降到V r（读数）而不改变悬臂。与静态犁刀光刻方法相比，DPL 的尖端磨损被证明是非常小的，因此可以忽略不计。通过避免更换探针和寻找纳米结构的位置，这种原位成像方法可以提高划痕过程的效率。所有实验均在室温下进行。

结果与讨论

考虑到 AFM PZT 的速度限制，在实验测试中选择了 0.1 到 1000 μm/s 范围内的划痕速度。图 1 显示了纳米加工过程的示意图，包括三个速度范围。当以相对较大的速度（大约每秒几百微米）刮擦时，会形成单独的凹坑，如图 1b 所示。当刮擦速度减慢到中等值（大约 100 μm/s）时，凹坑可以相互重叠，如图 1c 所示。如图 1d 所示，当划痕速度达到相对较小的值（每秒几十微米）时，凹坑可以转化为纳米凹槽。该结果表明，两个制作的凹坑之间的距离取决于划痕速度，这对制作的纳米图案有很大的影响。

在这项研究中，选择了四种典型的刮擦方向，如图 2a 所示。 V 1 和 V 3代表沿悬臂长轴的划痕； V 2 和 V 4 定义为垂直于悬臂长轴的划痕。尖端轨迹是通过控制 AFM PZT 获得的。图 3 显示了不同划痕速度制备的方线纳米结构的 AFM 图像和相应的纳米结构沿 V 方向划伤的横截面 1，当悬臂的共振频率为 380 kHz 时。在 200 μm/s 的相对较大的刮擦速度下，可以形成连续的凹坑，如图 3a 所示。对于预先设定的四个刮擦方向，即使刮擦速度在两个方向的转折点滑开，也会在远小于1秒的时间内立即形成凹坑。在中等划痕速度（100 μm/s）下，沿加工路径没有发现明显的凹坑，形成了波动的纳米结构，如图 3b 所示。在相邻的两条划痕路径的交叉处只能观察到一个深度更大的坑，可以解释如下。在相邻两个划痕路径转换期间，划痕速度应减慢至0，并且尖端比划痕时可以更多次压入样品表面，这可能是产生更大深度的可能原因坑的。 100 μm/s 的划痕速度可以被认为是在 PMMA 薄膜上制造连续凹坑的临界值。图 3c 显示了划痕速度为 50 μm/s 的加工纳米凹槽。从加工后的纳米凹槽的横截面可以观察到，纳米凹槽的底部比较平坦，可以形成明显的纳米凹槽深度。此外，如图 3 所示，由于尖端在 PMMA 薄膜上犁过，因此在划痕过程中不会形成碎片，只能在凹槽的一侧或两侧形成堆积。此外，在不同方向刮擦时，所得纳米结构不同侧面的轮廓不一致，这与使用非对称尖端的静态光刻的结果相似。对于其他抗蚀剂材料，如 SU-8 或聚苯乙烯 (PS)，由于应力松弛模量不同，划痕速度的阈值将与 PMMA 膜不同。然而，它们的阈值可以按照与本研究相同的方法通过刮擦实验获得。

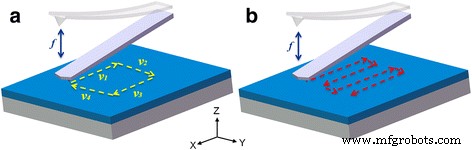
一 四种典型的刮擦方向（V 1、V 2、V 3、V 4) 在本研究中被选择用于纳米加工制造。 b 大面积图案进给的针尖轨迹

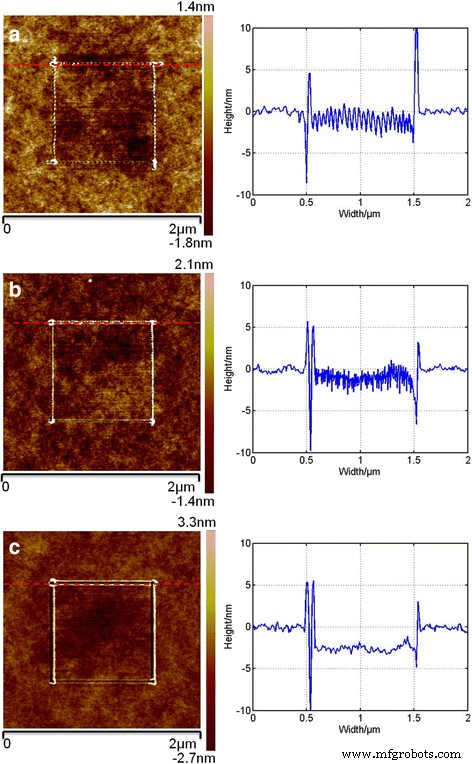
三种纳米结构的AFM图像及其在a划痕速度下的横截面 200 μm/s，b 100 μm/s 和 c 50 μm/s

划痕速度小于 100 μm/s，可以获得质量好的纳米凹槽。图 4 显示了在图 2a 所示的不同划痕方向下，纳米凹槽的加工深度与划痕速度之间的关系。对于每个纳米凹槽，实验深度由五个不同位置的五个深度值的平均值计算。所有刮擦方向的刮擦距离都相同——在本研究中为 1 微米。可以观察到，对于所有刮擦方向，加工深度随着刮擦速度的增加而减小。一种可能的原因可以解释如下。对于本研究中选择的 1 μm 刮擦距离，在 100 μm/s 和 1 μm/s 刮擦速度下的压机操作次数分别为 3870 和 387,000。对于相同的刮擦距离，AFM 尖端的大量压机操作会导致相邻压机操作之间的重叠百分比相对较大，从而导致纳米槽的加工深度更大。此外，如图 4 所示，当划痕速度小于 5 μm/s 时，在各个方向上划伤的纳米凹槽深度一致，而在 V 方向上加工的纳米凹槽深度 3 变得比其他方向获得的加工深度小得多，刮擦速度大于 5 μm/s。此外，在V方向获得的加工深度误差线 当划痕速度小于 5 μm/s 时，3 比其他的要大得多。一种可能的原因可以解释如下。本研究中使用的几何 AFM 探针是不对称的，并且由典型的 12° 悬臂斜率引起的探针倾斜，用于确保只有 AFM 尖端会接触样品表面，会导致接触面积的差异针尖和样品表面之间具有不同的刮擦方向。对于小于 5 μm/s 的刮擦速度，相邻冲压操作的重叠区域非常大。因此，尖端和样品表面之间的接触面积也非常大。因此，刮伤方向对加工深度的影响可以忽略不计。然而，沿尖端表面形成的堆积也取决于刮擦方向，这类似于静态刮擦过程。因此，在V中不能稳定地形成堆积 3 刮擦方向。图 4a、b 中插入的数字是典型纳米凹槽的横截面，分别以 0.5 和 50 μm/s 的刮擦速度加工。从以 0.5 μm/s 的划痕速度加工的纳米凹槽的横截面，在 V 中划痕时，纳米凹槽的底部是波动的 3 方向，这可能会导致加工深度的相对较大的误差条。对于速度大于 5 μm/s 的刮擦，与相邻冲压操作的重叠区域变小。因此，划痕方向起着重要作用，这会导致 V 中获得的加工深度相对较小。 3 刮擦方向。

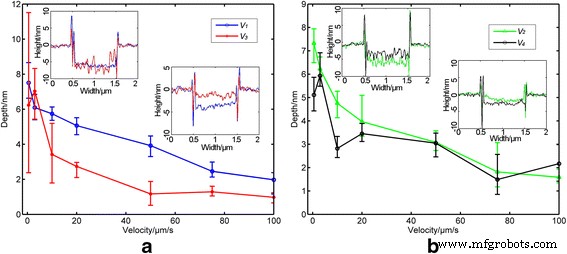
典型划痕方向上凹槽深度对划痕速度的依赖性：a V 1 和 V 3、平行于悬臂长轴； b V 2 和 V 4、垂直于悬臂长轴。插图显示了划痕速度为 0.5 和 50 μm/s 时纳米凹槽的横截面

PMMA薄膜是一种随时间变化的粘弹性材料。因此，AFM 尖端施加的周期性载荷可能会影响样品的杨氏模量。应力松弛模量G的一般表示 由 G 定义 1 和 G 2 [30]：

其中 G r 是一个常数，ω 与频率有关。 H (τ ) 是对应力松弛有贡献的松弛时间谱，它与 lnτ 之间的松弛时间有关 和 lnτ + d (lnτ ）。当激励频率设置为接近悬臂共振频率的值时，即 387 kHz，模量可以达到很高的值。根据使用上述方程的计算，PMMA 薄膜呈现为具有施加高频负载的玻璃态 [30]。由于整个加工过程采用敲击方式，因此在划痕过程中AFM尖端与样品表面之间的相互作用力和能量耗散较小，甚至驱动幅度V w/V r 设置为相对较高的值，范围从 10 到 20。在这些加工条件下，由于 PMMA 薄膜的玻璃状特性和 AFM 尖端施加的相对较小的负载，聚合物分子之间的链不能一次冲压操作，使试样表面发生变形，不易发生塑性变形。然而，尖端有足够的能量 (> 1~2 eV) 在前 20-30 次按压操作期间完成此操作 [27]。因此，可以切断聚合物分子之间的链键，从而在薄膜表面产生塑性变形。

相邻按压操作之间的间隔距离是一个关键参数，与刮擦速度和尖端的振荡频率有关。一条坑线的距离(L ) 可以通过一个坑线使用的时间 (t ) 乘以刮擦速度 (v ）。一个坑线中的 AFM 尖端振荡总数 (N ) 可以使用悬臂的振荡频率 (f ) 乘以时间 (t ）。因此，相邻按压操作之间的间隔距离 (D ) 可以通过等式获得。 4.

本研究中选择的悬臂的固有振动频率约为 387 kHz。 AFM 系统的驱动频率选择为接近该值。如上所述，划痕速度应选择在 200 到 900 μm/s 的范围内，以保证凹坑的形成。因此，相邻按压操作之间的间隔距离 (D e) 在划痕过程中可以在 0.52 到 2.33 nm 的范围内计算，这表示为图 5a 中的红色曲线。图 5a 中的蓝色曲线表示相邻凹坑之间的间距 (D ) 从实验和划痕速度中获得。插入的 AFM 图像是针对使用 400、600 和 800 μm/s 的三种典型刮擦速度加工的凹坑获得的。因此，一个凹坑形成的压力操作次数可以计算为D的比值 D e 显示在图 5b 中。假设划痕速度是一个恒定值，根据划痕长度 (L ) 和间距 (D ）。从图 5b 可以看出，随着刮擦速度的增加，一个凹坑形成的压力操作次数增加，并且大部分在 65 到 80 的范围内。考虑到两个凹坑之间的水平地形几乎等于在凹坑中，只需要大约 32-40 次压力操作就可以使聚合物链断裂，从而使样品表面产生塑性变形，这与 Cappella 的结论一致 [27]。此外，可以得出结论，当以相对较小的速度刮擦时，更容易破坏聚合物链。在这项研究中，悬臂的弹簧常数是相同的。更硬的悬臂可用于制造凹坑，从而产生更大的外加力和更高的共振频率。如果对样品表面施加更大的力，则每个循环中的能量输入都会增加。因此，更多的能量耗散有助于 PMMA 膜的变形。因此可以以减少的周期产生一个凹坑。然而，如果振荡系统的共振频率增加，则样品表面和尖端之间的按压操作的周期因此增加。此外，由于实验中设定点的降低，能量耗散会在一个循环中增加。临界速度可由设定点的值确定。综上所述，速度阈值可能受作用力、悬臂系统共振频率和设定点的影响，这将是未来研究的重点。

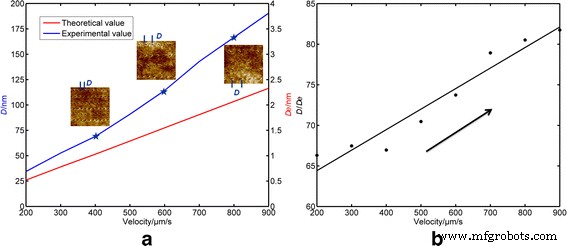
一 D 的变体 和 D e 具有刮擦速度（200–900 μm/s）；插图显示了各种划痕速度的制造结果。 b D 的比例 D

坑的形成过程如图 6 所示，包括三个阶段：弹性变形、塑性变形和越过堆积物。根据上述讨论，在尖端划过图 6a、b 的距离期间，按压操作的次数不足以破坏 PMMA 薄膜的聚合物链并产生样品表面的塑性变形。已经证明，在前 40-50 次操作期间，振荡尖端逐渐渗透到聚合物样品中 [27]。与参考文献中的压痕过程相比。 [27]，以横向速度按压可以在两个相邻的穿透之间产生距离。然而，两个相邻穿透之间的距离（在 0.52 到 2.33 nm 的范围内）远小于 AFM 尖端的半径（大约 15 nm）。因此，本研究中的情况类似于压痕过程的情况。由于在最初的 30-40 次穿透过程中缺乏能量积累，在加工区域没有发现明显的塑性变形。该结果表明，能量耗散的主要机制是划痕第一阶段的弹性变形。因此，在图 6a、b 之间的时间段内，AFM 尖端与样品表面持续接触滑动。当 AFM 尖端进行的穿透次数达到临界值（本研究中为 40 次）时，聚合物链开始断裂并发生塑性变形，如图 6c 所示。同时，AFM 探针前端与样品材料的相互作用面会产生法向应力和剪切应力；因此，可以在 AFM 尖端的前面前面产生堆积。会发生应变 (Δ)，这归因于对抗堆积的横向尖端运动。这将导致聚合物薄膜内部产生应力，该应力可能通过裂纹的传播而释放[31]。应变能释放率V s 可以描述为：[32]。

其中 E 是聚合物材料的杨氏模量，L 是内部缺陷长度。 h 代表样品自由表面的总穿透深度。表面能项W 控制内部缺陷过程，它等于通过热力学平衡的应变能释放率。表面能项取决于内部缺陷的传播速度 (v L)，由[33]给出。

其中 v L 等于 dL /dt 和 α 是与样品材料相关的常数值。 n 也是一个材料相关的参数。施加在尖端的切向力可以由聚合物基底中储存的弹性能产生，可以表示为[32]：

其中 a 表示针尖和样品之间接触区域的半径。由于探针刚度远大于样品的刚度，因此可以从形成的孔中移除材料 [31]。然而，Mindlin 定义了可能导致尖端在基板表面滑动的力的临界值 [34]。临界切向力 (F tc) 对于滑动可以确定为粘附力和法向载荷的函数，表示为 [35,36,37,38]：

其中 μ 是摩擦系数。 P 是正常的，R 表示 AFM 尖端的半径。当 F t 达到临界值 F tc，AFM 尖端会滑过材料的堆积，而不是将材料推出尖端产生的孔。接触在每个循环中都断开，因此，在攻丝模式中的每个循环中更容易发生滑动。虽然设定点没有接近100%的尖端振荡减少，但在一个循环中可能会出现一段时间的接触，在这段时间内可能会发生粘连。

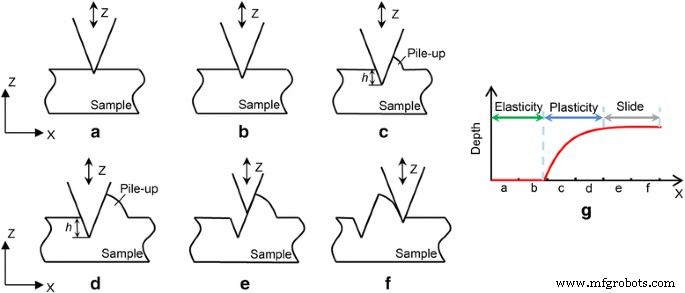
a形成的凹坑示意图 , b 弹性阶段，c , d 塑性阶段，e , f 幻灯片阶段，和g 凹坑形成顺序图

如图 6d 所示，在本研究中，由于 AFM 尖端承受横向速度时尖端-样品接触面积的减少，AFM 尖端穿透样品表面的深度变大。堆积的高度也增加了。这可能有助于平衡 AFM 尖端施加的正常负载。同时，施加在等式中描述的尖端的切向力。 7 could also be increased. With an increasing penetration depth, the tangential force could reach the critical value F tc given in Eq. 8. The AFM tip starts to slide on the formed pile-up without modifying the material. Because of the characteristics of the tracking sample surface of the AFM system, the AFM tip would rise to climb over the pile-up, as shown in Fig. 6e. After the AFM tip moved over the pile-up, one pit could be achieved and another pit would be fabricated by repeating the above steps. The corresponding deformation mechanism of each stage of pit formation can be found in Fig. 6g.

According to the previous experimental results, the scratching velocity should be set to larger than 100 μm/s. As shown in Fig. 2b, scratching directions V 1 and V 3 are selected and a feed perpendicular to the scratching direction is conducted to achieve pit arrays with a large dimension of 5 μm. Figure 7a shows the pit arrays obtained with a scratching velocity of 400 μm/s. Figure 7b, c shows the local and 3D AFM images of the machined pits, respectively. Because the scratching velocity slows down to 0 near the transition point of two different scratching directions, the depths of the first and last pits of one horizontal scratching path are much larger than the pits in the middle. One possible reason is explained above. As shown in Fig. 7b, c, the pits in the middle of the scratching path are distributed evenly, which may result from the constant velocity. Moreover, it can be observed from the cross-section of the pits shown in Fig. 7d that the depths of the pits are approximately 2.5 nm. In addition, because of the opposite scratching directions of the adjacent paths, the geometries of the pits in adjacent lines are different. As shown in Fig. 8a, with a scratching velocity of 200 μm/s, the spacing distance between the adjacent pits is relatively small and the geometries of the pits are close to circular. From the fast Fourier transform (FFT) image of the pits, high-density pits can be obtained with a scratching velocity of 200 μm/s. When scratching with a velocity of 900 μm/s, as shown in Fig. 8b, the spacing distance is nearly 100 nm and differences between pits obtained with different scratching directions can be clearly observed. Also from the FFT image of the pits, with a scratching velocity of 900 μm/s, only low-density pits can be achieved.

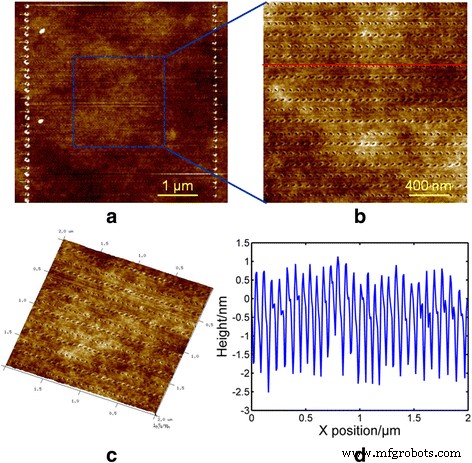
AFM images of an array of pits with a scratching velocity of 400 μm/s, a a dimension of 5 μm, b a portion of a with a dimension of 2 μm, c a 3D AFM image of b , 和 d a cross-section of pits for the red line in b

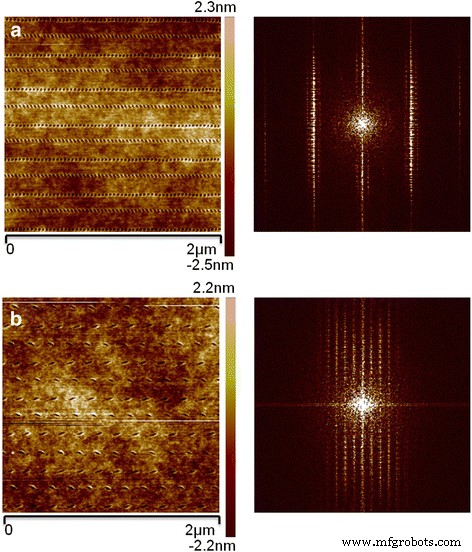
AFM image of pit arrary with a dimension of 2 μm and FFT image of the morphology. The scratching velocities are a 200 μm/s and b 900 μm/s

结论

To improve the fabrication efficiency with the tip-based DPL method, a scratching velocity that ranges from 0.1 to 1000 μm/s is investigated and demonstrated based on the commercial AFM tapping mode. In the present study, results demonstrate that 100 μm/s is the critical value of the scratching velocity for the formation of pits. Nanogrooves with a pile-up can be obtained with scratching velocities less than the critical value. With scratching velocities greater than 5 μm/s, the machined depths are consistent in all typical directions except the V 3 direction, in which the machined depth becomes much smaller. In contrast, the depth is independent of the scratching direction. Separate pits can be generated with scratching velocities larger than the critical value of 100 μm/s. The total number of fabricated pits can reach nearly 4800–5800 in 1 s, when the scratching velocity is a constant value ranging from 200 to 900 μm/s. According to the stress relaxation modulus theory, the polymer surface is in the condition of a glass state when applying a high-frequency load. The energy applied on the sample surface is not large enough to break PMMA molecular chains during one penetration of the AFM tip. To form one pit, 65 to 80 penetrations are required. For the initial stage of penetration, elastic deformation is the dominant material removal mechanism. When the number of penetrations reaches 40 times, the polymer chains start to break and plastic deformation occurs. With increasing penetration depth, the height of the material accumulated beside the machined pit becomes larger, which will lead to an increase in the tangential force applied on the tip apex. This is the possible reason for the AFM tip sliding over the pile-up, after which one pit is created. Finally, pit arrays with dimensions of 5 μm, spacing distance of 70 nm, and machined depth of 2.5 nm are achieved successfully. FFT images are used to reveal the relationship between the density of pits and the scratching velocity.