SnxPy 单层：一种具有高稳定性、载流子迁移率和磁性的新型二维材料

摘要

寻找具有铁磁性、弹性各向异性、载流子迁移率和可调能带结构的二维 (2D) V 族材料是不断发展纳米器件的关键之一。带有 x 的二维单层 SnxPy /y (1/1、1/2、1/3等)配位数基于粒子群优化技术结合密度泛函理论优化进行研究。其热稳定性可通过70K和300K的分子动力学证实，表明新型二维材料稳定存在。四种稳定结构的电子能带结构表明，在双轴应变下，SnxPy 的所有单层都是完全可调且灵活的可调带隙半导体。由于“斯托纳准则”，具有独特价带结构的 P$ \overline{4}{2}_1 $m-SnP2 单层可以通过空穴掺杂从非磁性变为铁磁性，而 Pmc21-SnP2 是直接具有面内弹性各向异性的类间隙半导体，具有高达 800 cm² 的高电子迁移率 V⁻¹ s⁻¹ 沿着 k b 方向，远高于 MoS2 (∼ 200 cm² V⁻¹ s⁻¹ ）。该材料的光吸收峰在紫外区。这些发现拓展了二维SnxPy结构在纳米电子领域的潜在应用。

介绍

二维（2D）二元化合物由于其独特的性质近年来引起了广泛关注，并且可以为其在纳米电子和光电器件中的潜在应用提供可靠的指导[1]。例如，石墨烯因其性质和潜在应用而被发现后引起了极大的兴趣 [2,3,4,5,6]，而石墨烯在室温下具有不可检测的小带隙，使其难以用于光电纳米器件。因此，这些困难促使研究人员决心寻找具有理想带隙的二维材料。在接下来的几年里，氮化硼 (BN) [7]、MoS2 或其他过渡金属二硫属元素化物 [8,9,10,11,12,13] 和过渡金属三硫属元素化物 [14, 15] 等出来了。近年来，石墨烯和第IV族的其他二维材料（硅胶、锡烯和锗烯[16]）在科学研究中取得了良好的进展。除此之外，属于 V 族的二维半导体材料，尤其是磷烯 [17,18,19] 和砷烯 [20]，正在成为光电器件领域的新一代竞争者。磷烯在场效应晶体管、光电器件、自旋电子学、气体传感器和太阳能电池等方面具有广阔的应用前景，而二维蜂窝状结构的锡烯被认为是继石墨烯之后具有优异物理性能的新型材料由于其强的电子自旋轨道耦合。

迫切需要合成两种元素以获得多功能新型二维材料。据悉，合金化常被用于改善二维材料的性能以扩大其适用性。例如，二维 MoS2xSe2(1 − x ) 和 WS2xSe2(1 − x ) 纳米片 [21, 22] 见证了奇怪的特性，如可调电子、光学特性和与 x 的面内负泊松比 /y （1/1、1/2、1/3 等）协调号。再例如，二维合金材料SixCy [23]、BxCy [24]和BxSiy [25]通过第一性原理计算显示出许多不同于纯地面的新特性（新颖的结构、电子和机械性能）状态。由于二维磷烯和锡烯单层具有新的性质，Sn和P元素以多种化学计量进行复合。

在这项工作中，我们通过粒子群优化 (PSO) 算法构建了一些结构。然后，我们挑选出具有不同配位数的四种最稳定的二维 SnxPy 单层结构，并在密度泛函理论 (DFT) 优化的基础上研究了电子特性。计算出的电子能带结构表明，所有具有不同配位数的稳定或亚稳态单层都是具有间接带隙的半导体。更重要的是，Pmc21-SnP2 单层是一种类似直接的带隙半导体，在红外光区域具有 0.92 eV 的有限带隙。但除此之外，Pmc21-SnP2 结构是一种类似直接的间隙半导体，具有 ~ 800 cm² 的高电子迁移率 V⁻¹ s⁻¹ , 远高于 MoS2 (∼ 200 cm² V⁻¹ s⁻¹ ）。由于“斯托纳准则”，具有独特价带结构的 P$ \overline{4}{2}_1 $m-SnP2 结构的单层可以通过空穴掺杂从非磁性变为铁磁性。计算的电子能带结构表明，SnxPy 的所有单层都是在双轴应变下具有灵活可调带隙的半导体，允许在几乎整个可见光范围内对四种结构带隙进行应变工程。

计算方法

为了保证对结构多样性的彻底搜索，各种x 和 y 根据粒子群优化 (PSO) 算法 [26]，从一到六中进行选择。单层结构的搜索结果仅对于 y 相对稳定 /x ≧ 1.

为了研究具有不同配位数的 2D SnxPy 单层的电子结构，我们使用平面波密度泛函理论 (DFT) [27, 28] 方法在 Vienna Ab-initio Simulation Package (VASP) 中实现了计算。 29,30,31]。通过广义梯度近似 (GGA) 以 Per-dew-Burke-Ernzerhof (PBE) [32,33,34,35] 的形式描述交换相关能，并通过投影放大描述电子-离子势波法[33]。对于 SnxPy 系统，平面波的截止能量分别选择为 500 eV 能量。在布里渊区对互易空间的一个足够密集的 k 点 (9 × 9 × 1) 进行采样。相邻超级单元之间垂直于平面的真空空间大于 25 Å，消除了复制之间的相互作用。在连续两步计算中，设置为10⁵ eV 作为能量收敛值。在几何优化过程中，所有结构的原子力都小于0.02 eV Å⁻¹ 通过使用共轭梯度法，直到原子到达它们的最佳位置。此外，当Nosé算法[36]在300K时，我们将使用4×4×1的超胞进行从头算分子动力学（AIMD）计算。

载流子迁移率主要受声侧波散射、光侧波散射和电离杂质散射的影响。由于后两者的影响不如第一个，所以我们计算的迁移率包括声侧波散射下的迁移率。迁移率主要影响晶体管的两个性能：一是载流子浓度共同决定了半导体材料的电导率（电阻率的倒数）。其次，它影响设备的工作频率。双极晶体管频率响应特性的主要限制是少数载流子穿过基区的时间。迁移率是衡量二维半导体材料电导率的重要参数。它决定了半导体材料的导电性并影响器件的工作速度。因此，载流子迁移率受声子色散控制，可以通过 Bardeen 和 Shockley [37] 提出的变形势 (DP) 理论来描述。因此，二维材料中的载流子迁移率可以表示为 [38, 39]

$$ {\mu}_{2D}=\frac{2e{\mathrm{\hslash}}^3{C}^{2D}}{3{k}_BT{\left|{m}^{\ast }\right|}^2{E}_1^2} $$

其中 e 、 ℏ 和 k B 分别是电子电荷减少的普朗克常数和玻尔兹曼常数。和 T 是设置为 300K 的温度。其中 m* 是有效质量，E 1 为变形势常数，C ^二维是面内刚度。

小波矢量下系统对光场的线性效应由复介电常数的虚部和介电函数决定，介电函数可由下式计算

$$ \upvarepsilon \left(\omega \right)={\varepsilon}_1\left(\omega \right)+i{\varepsilon}_2\left(\omega \right) $$

其中 ε 1(ω ) 和 ε 2(ω ) 是函数的实部和虚部，ε 1(ω ) 可以从虚部 ε 导出 2(ω ) Kramer-Kronig 的介电函数可以表示为 [40]。介电函数的虚部可表示为

$$ {\varepsilon}_2\left(\omega \right)=\frac{4{\pi}^2}{m^2-{\omega}^2}\sum \limits_{V,C}\underset {BZ}{\int }{d}^3k\frac{2}{2\pi }{\left|e\bullet {M}_{cv}\right|}^2\times \updelta \left[{ E}_C\right.(k)-{E}_V(k)-\mathrm{\hslash}\left.\omega \right] $$

此外，吸收系数I (ω ) 是通过

$$ I\left(\omega \right)=\sqrt{2}\omega \left[\sqrt{\varepsilon_1^2\left(\omega \right)-{\varepsilon}_2^2\left(\omega \right)}-{\varepsilon}_1\left(\omega \right)\right]1/2 $$

其中 C 是导带，V 是价带态，Ω 是晶胞体积，m 是自由电子的质量，e 是自由电子的电荷，ω 是入射光子的频率。

结果与讨论

稳定性

首先，考虑了四个 2D SnxPy 单层来确定它们的能量稳定性。地层能是热力学系统中的一个能量参数，是检验系统稳定性的关键。 SnxPy单层的相对稳定性可以通过计算形成能来确定，计算公式为

$$ {E}_{\mathrm{form}}=\left({E}_{\mathrm{total}}-{N}_{\mathrm{Sn}}{E}_{\mathrm{Sn} }-{N}_{\mathrm{P}}{E}_P\right)/\left({N}_{\mathrm{Sn}}+{N}_{\mathrm{p}}\right) $$

其中 E 是化合物或组成元素在特定压力下的能量。 N 是晶胞中的原子数。计算系统的负形成能表明构型稳定或亚稳态[41]。 SnxPy 单层的计算形成能分别为 - 0.235、- 0.223、- 0.159 和 - 0.016 eV/原子（如表 1 所示）。根据其定义，较小的值表示较高的稳定性。显然，P$ \overline{6} $m2-SnP 是这四种结构中最稳定的。更具体地说，半导体材料的高热稳定性在电子器件的应用中尤为重要。在这里，SnxPy 单层的热稳定性通过使用从头算分子动力学 (AIMD) 模拟来检查。基于空间群的对称性，我们只需计算 P$ \overline{6} $m2-SnP 对于相似结构 P$ \overline{6} $m2-SnP 和 Pmc21-SnP2 和 Pmc21 的稳定性-SnP2 用于 Pmc21-SnP2 和 P$ \overline{4}{2}_1 $m-SnP2 结构。结果表明，结构总能量的平均值几乎保持不变，1 ps、3 ps和5 ps后结构保持不变，表明SnxPy单层是热稳定的（图S1）。然后，我们计算了声子色散曲线并且没有虚振动频率意味着结构是动态稳定的（在图 S1 中）。文献中已经报道了几种合成层状材料的方法，包括微机械解理 [2]、外延生长 [42]、化学气相沉积 [43] 和液体剥离 [44]。通过实验成功制备了一些结构相似的材料。我们发现了一些相关报道，在实验中很少有层GaSe纳米片被制成高性能光电探测器[45]。此外，还报道了沉积在 SiO2/Si 衬底上的大尺寸 MoS2、GaS 和 GaSe 超薄层的制备、隔离和快速明确表征[46]。

如图 1a、b 所示，P$ \overline{3} $m1-SnP 的结构表现出类似于 P$ \overline{6} $m2-SnP 六方相的结构。 Pmc21-SnP 2 三角相（图 1c）表明 x /y 成分进一步增加到1/2。通过理论计算证明了类似于 P$ \overline{4} $21m-SnP2 结构的材料是稳定的 [47]。此外，一项新研究发现 XY2 的结构（图 1d）是一种间接带隙半导体，它可能容易受到电场和应力的影响。我们相信，随着技术的发展，我们预测的材料在未来会得到成功的制备。

<图片>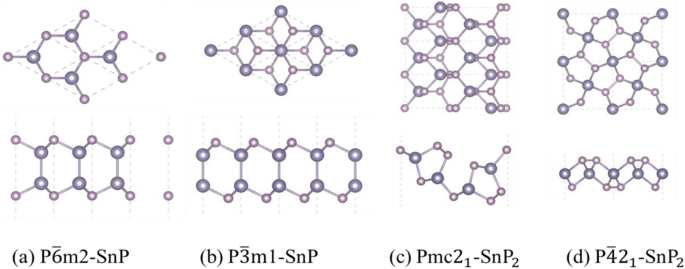

SnxPy 单层原子结构的顶视图和侧视图：a P$ \overline{6} $m2-SnP, b P$ \overline{3} $m1-SnP, c Pmc21-SnP2 和 d P$ \overline{4}{2}_1 $m-SnP2;费米能级（水平虚线）移动到 0 eV。深粉色球体代表Sn原子，浅粉色球体代表P原子

电子和磁性属性

SnxPy 单层的计算能带结构和部分态密度绘制在图 2 中。如图 2a 所示，P6̅m2-SnP 是一种间接半导体，带隙为 1.19 eV。 Γ → K 方向的价带最大值 (VBM) 由杂化的 Sn-p 和 P-p 轨道贡献，而 K 点的导带最小值 (CBM) 来自杂化的 Sn-s 和 P-p 轨道。 P$ \overline{3} $m1-SnP 表现出与 P$ \overline{6} $m2-SnP 对应物相似的电子能带结构，但带隙较小，为 1.21 eV。 P$ \overline{6} $m2-SnP 和 P$ \overline{3} $m1-SnP 在 Γ 点和费米能级附近的价带色散 (E F ) 是相当平坦的，因为状态密度 (DOS) 和 VBM 周围的范霍夫奇点相当高。 Pmc21-SnP2 表现出类似直接的间隙半导体特性 (E g(direct) - E g(indirect) =6 meV)，带隙为 0.72 eV（见图 2c）。其 VBM 主要归因于 P-p 轨道，而其 CBM 主要由 P-p 轨道和 Sn-s 轨道贡献。 P$ \overline{4}{2}_1 $m -SnP2 是一种具有 E 的间接带隙半导体 g 的 1.79 eV，从带派生类似于图 2c。更重要的是，P$ \overline{4}{2}_1 $m-SnP2monolayer 与图 2a、b 具有相似的条件，在 VBM 周围也出现了平带色散特征，导致非常高的 DOS 和范霍夫奇点。

<图片>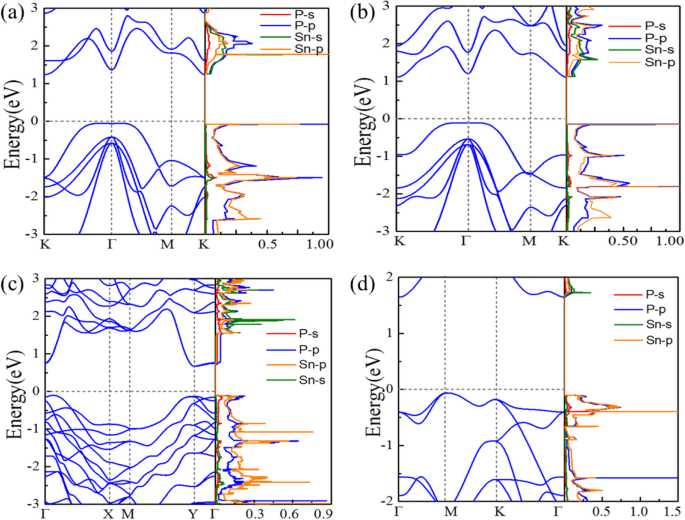

SnxPy 单层的 VBM 和 CBM 的计算电子能带结构和部分态密度：a P$ \overline{6} $m2-SnP, b P$ \overline{3} $m1-SnP, c Pmc21-SnP2 和 d P$ \overline{4}{2}_1 $m-SnP2

根据斯通纳准则，如果动能小于交换分裂能，即如果 E 处的 DOS，就会发生自发铁磁性 F 足够高。图 2d 显示了 VBM 周围非常高的 DOS； P$ \overline{4}{2}_1 $m-SnP2 可能满足 Stoner 准则，如果它的 E F 转移到具有高 DOS 通孔掺杂的位置。如图 3a 所示，空穴掺杂可以在适当的掺杂浓度下引入磁矩。正如预期的那样，计算结果表明 P$ \overline{4}{2}_1 $m-SnP2 可以转换为超过临界孔密度的铁磁基态。其中，空穴密度n h 可以表示为 n h =米 h /S 单元格 , 其中 S 单元格 和 m h 是原始细胞的面积和原始细胞中引入的孔的数量。将空穴注入单层 P$ \overline{4}{2}_1 $m-SnP2 确实会导致铁磁性。磁矩与空穴密度呈现陡峭的峰状关系。由于系统中的空穴掺杂会引起可观的自旋力矩，因此费米能级周围的能带结构由于自旋分裂而发生了很大变化。特别是，P$ \overline{4}{2}_1 $m-SnP2 在 7.2 × 10¹⁴ 的自旋极化带结构（如图 3b 所示） cm⁻² 表明单层变成了完美的半金属。因此，我们预测可以在 P$ \overline{4}{2}_1 $m-SnP2 单层中实现具有半金属丰度的稳定 FM 状态。

<图片>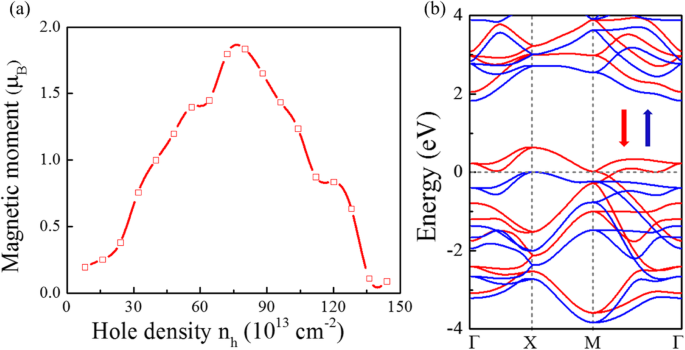

P$ \overline{4}{2}_1 $m-SnP2 单层中的铁磁性。 (a ) 自旋矩与孔密度 n h . b 在 n 处计算 P$ \overline{4}{2}_1 $m-SnP2 的价带结构 h =7.2 × 10¹⁴ cm⁻² .自旋和自旋带分别以蓝色和红色显示。费米能级设置为 0 eV

单层的弹性各向异性和载流子迁移率

应变对二维单层 Snx 电子特性的影响 Py 结构也很有趣。图4a为双轴应变ε下的能隙变化 . SnxPy 单层的能隙根据一些规则显着调制。例如，随着拉伸应变增加到 ε，P$ \overline{6} $m2-SnP 的能隙从 1.19 减小到 0.52 eV =8%，对于 ε，首先从 1.12 增加到 1.36 eV 2%，然后从 1.36 下降到 0.51 eV。此外，由于 a 和 b Pmc21-SnP2结构的晶格参数不同，沿x的电子性质变化不同 -axis 和 y -轴[48]，如图4b所示。很明显，当在不同方向施加单轴应变时，x 方向与 y 的变化不同方向。考虑应变ε的能隙范围，基于第一性原理计算，面内应变可调带隙的范围几乎覆盖了整个可见光区域。

<图片>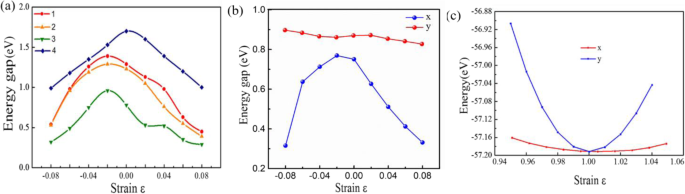

结构的应变相关电子特性：(1) P$ \overline{6} $m2-SnP，(2) P$ \overline{3} $m1-SnP，(3) Pmc21-SnP2，和(4) P$ \overline{4}{2}_1 $m-SnP2。 b Pmc21-SnP2 的单轴应变相关电子特性。 c Pmc21-SnP2单层与单轴染色的能量

此外，我们还研究了单轴应力的影响，如图 4c 所示。面内刚度 C ^二维 (C ^二维 =[∂² E /∂δ ² ]/S 0，其中 S 0 是 2D Pmc21-SnP2 单层的面积）可以通过拟合抛物线获得。有趣的是，面内刚度 C ^二维沿a表现出极其明显的弹性各向异性和 b 方向分别计算为 12.1 和 105.6 N/m。由于 Pmc21-SnP2 表现出类似直接的间隙半导体特性，有效质量 (m ^* =ℏ ² (∂ ² E /∂K ² )⁻¹ ) 个电子 (m e 是 |m ^* e|) 和孔 (m h 是 |m ^* 还计算了与（准）直接半导体 Pmc21-SnP2 单层相关的 h|)。列出了有效质量（表 2）。最有趣的是 k 中电子的有效质量 b 方向 (0.15 me) 远小于 k 一方向（1.31 me），表明电子在k中容易漂移 b 方向。还有一个重要的参数是DP常数E 1 (E 1 =dE 边缘/dδ ) 对于沿 a 的电子和 b 方向分别计算为 5.36 和 11.57 eV。令人惊讶的是，计算出的载波可以达到~800 cm² V⁻¹ s⁻¹ 在 k b 方向。作为对比，MoS2 单层的载流子迁移率约为 200 cm² V⁻¹ s⁻¹ 在实验中[8]。然而，载流子迁移率仅为 ~ 8 cm² V⁻¹ s⁻¹ 在 k 一方向。因此，本研究发现的高载流子迁移率对电子传输的研究具有重要意义。

光学性质

光电材料的光电特性由介电函数、光电导率和吸收系数表征。介电函数的虚部如图 5a 所示。请注意，Pmc21-SnP2 单层显示从~0.70 eV 开始的吸收，并且在~0.9、~3.2 和~4.0 eV 处出现三个主要吸收峰。如图 5b 所示，它显示了单层 Pmc21-SnP2 在可见光范围和紫外范围内所有三个方向的吸光度。因此，Pmc21-SnP2单层材料可用于原子级薄的日盲光电探测器，例如有效探测火焰。

<图片>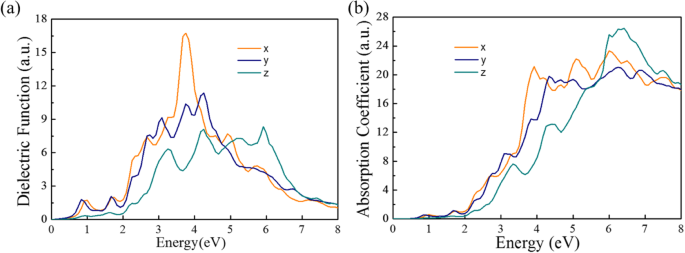

一 Pmc21-SnP2 沿不同入射光方向计算的介电函数与能量的关系。 b 计算虚吸收系数

结论

总之，基于PSO算法结合第一性原理计算，我们已经确定了几个具有x比率的二维SnxPy单层 /y =1:1 和 1:2。令人惊讶的是，这些新型单层还具有独特的电子和磁性特性：具有独特价带结构的 P$ \overline{4}{2}_1 $m-SnP2 结构的单层可以通过空穴掺杂从非磁性变为铁磁性，因为“斯通纳准则”； Pmc21-SnP2结构是一种具有面内弹性各向异性的类直接间隙半导体，被发现具有高达800 cm² 的高电子迁移率 V⁻¹ s⁻¹ 沿着 k b 方向，远高于 MoS2 (∼ 200 cm² V⁻¹ s⁻¹ ）。该材料的光吸收峰在紫外区。这些发现扩展了 2D SnxPy 结构在纳米电子学中的新兴领域的潜在应用。多功能SnxPy单层的这些理想特性为电子和光电子学提供了广阔的应用前景。

数据和材料的可用性

它们都在正文和图表中。

不同厚度的二维 (2D) 矩形和六边形二氧化钼纳米片的比较研究共同加入臭氧和去离子水作为通过原子层沉积生长 ZnO 薄膜的氧化剂前体

纳米材料