胶体高掺杂 ZnO 纳米晶体的光吸收中的等离子体共振

背景

在很大程度上，纳米粒子的光学特性是由其激发光谱中局部表面等离子体共振 (LSPR) 的存在决定的 [1-8]。克里格尔等人。 [2] 发表了对新兴胶体纳米晶体 (NCs) 的非常详细的概述，包括杂质掺杂的金属氧化物 NCs、铜硫属化物 NCs 和简并掺杂的半导体 NCs，并广泛讨论了它们的光学特性以及传感、近场应用增强光谱、可调谐光电器件或生物医学应用。所有这些新材料都是过去几十年被广泛研究的贵金属 NC 的替代品；有关全面审查，另见参考文献。 [9]。已经表明，通过作用于各种控制参数 [11, 13, 16-20]，可以将重掺杂半导体纳米晶体 (NCs) 的光学响应调整到红外范围 [10-15]，从而打开纳米光子学的新视角。半导体 NC 的主要优点是载流子密度可以在很宽的范围内进行调整。金属导体具有固定的电子密度，而半导体可以掺杂以实现 10 ¹⁶ 范围内的任意载流子密度 ÷10 ²² 厘米 ⁻³ [10, 13, 21, 22]。载流子掺杂允许在从太赫兹到红外和可见光区域的宽频率范围内获得可调谐 LSPR [13]。这种载流子密度可调性是半导体纳米粒子的独特属性，无法使用金属液滴实现 [23-25]。掺杂可以通过在晶格中加入各种类型的杂质来完成 [7, 10, 18]，并且等离子体共振频率可以通过载流子的主动控制来调整或切换 [13, 16–18, 21, 22]。此外，等离子体频率及其线形不仅取决于 NC 的载流子密度，还取决于掺杂类型，可以是“块状”或“表面状”[15, 22]。在前一种情况下，自由载流子的电荷被整个 NC 体积中的掺杂杂质电荷中和，而在后一种情况下，自由载流子由位于周围介质的施主/受体注入 NC 体积。数控接口。

半导体纳米粒子光学响应的​​理论研究揭示了量子力学和经典描述之间的显着差异 [5, 22, 24, 26]。随着纳米颗粒尺寸的减小，等离子体共振转移到更高的能量，与经典预测的明显偏差 [5, 21, 22]。此外，高掺杂 NC 的动态特性经历了从尺寸量化机制到等离子体振荡经典机制的转变 [22]。可以通过改变载体数量或NC大小来观察。

在这项工作中，我们对光掺杂的 ZnO NCs 的光学响应进行了理论分析，例如在参考文献中进行了实验研究。 [21, 27]。在这些实验研究中，测量了固定尺寸和载流子密度的胶体 ZnO NC 的光吸收截面。通过光掺杂工艺在 ZnO NC 中产生导带光电子，而空穴被周围甲苯中的空穴清除中心捕获。平均导电电子浓度n e 在几乎球形的不同半径（1.75 到 6 nm）光掺杂纳米晶体中，发现其上限为（1.4±0.4）×10 ²⁰ 厘米 ⁻³ [21, 27]。带内吸光度的测量范围为 0.2 到 1.0 eV，观察到与经典 Drude 模型预测的显着差异。作者表明，基于单粒子跃迁的量子力学方法只能定性地产生共振频率的实验尺寸依赖性 [21]。

本文的目的是通过超越非相互作用的单粒子近似，重新审视光掺杂 ZnO NCs 中等离子体共振的理论方法 [21, 27]。它基于具有局部交换的随机相位近似 (RPA) 内传导电子的自洽多体量子力学处理 [28]。结果表明，半导体纳米粒子中的自由载流子形成原子状壳[29, 30]。我们求解局部密度近似 (LDA) Kohn-Sham 方程来描述电子壳结构。在 RPA 中考虑了负责集体等离子体激发的电子相关性。我们表明，ZnO NC 中的等离子体共振与金属液滴中众所周知的 Mie 共振有很大不同。与体状掺杂的 NCs 不同，表面状掺杂的 ZnO NC 中没有恢复正电荷。因此，自由电子之间的库仑排斥力将它们推近 NC 表面。反过来，这种特定的电子配置导致偶极子模式，其中仅激发角自由度，而不涉及电子径向运动。与电子经历纯平移振荡的普通 Mie 表面偶极等离子体相反，高掺杂 ZnO NC 中的电子在相当薄的电子壳内以类似于富勒烯分子中的等离子体振荡的方式经历切向振动 [31]。我们还表明，这种等离子体模式从经典到量子限制机制的转变受 NC 尺寸与有效玻尔半径的比率控制，而不取决于自由电子的数量。等离子体振荡中的量子效应导致偶极共振频率的蓝移，这与实验观察到的 LSPR 尺寸依赖性非常吻合 [21]。

方法

本研究的目的是对光掺杂 ZnO 纳米晶体的光学特性进行理论分析。在局部密度近似内计算具有不同数量粒子的系统的基态配置。基态波函数是单粒子能量，它是通过一组 Kohn-Sham 方程组的自洽数值求解获得的 [32]。单粒子状态的完整基是使用 B 样条方法 [33] 通过在有限数量的 B 样条上扩展大半径腔中的基函数来生成的。选择的腔半径等于 NC 半径。 The desired accuracy of the computations with the use of the B-spline discrete basis was achieved by the appropriate choice of the number and the order of the B-splines used in the computation.我们使用了 50 个 7 阶 B 样条来达到足够的精度 (10 ⁻⁵ ) 的结果。特征系统子程序包 (EISPACK) 中的标准子程序 RG 已用于获得 RPA 矩阵方程 [28] 的特征值和特征向量，该解决方案为我们提供了一组偶极子激发能量和相应的振荡器强度。通过固定折叠宽度的洛伦兹分布对计算的振荡强度分布进行展宽，得到光吸收光谱。

结果与讨论

地面结构

我们考虑N的系统 位于半径 R 的 ZnO NC 内的导带电子 .根据[21]，我们假设电子数随 NC 尺寸变化为 N =4π n e R ³ /3，其中固定平均电子浓度，n e =1.4×10 ²⁰ 厘米 ⁻³ , 由光掺杂过程中可达到的最高水平决定。所考虑的 NC 的半径范围为 2.4 到 6 nm；因此，传导电子的数量，N , 从 8 到 128 不等。

我们采用包络函数近似来描述电子运动，假设 R 远大于晶格常数。众所周知，块状 ZnO 的电子能带结构的特征在于非各向同性和非抛物线能谱 [34]。然而，对于当前N的集体动力学问题 离域电子，我们将忽略这些小的能谱效应，并考虑具有有效质量 \(m_{e}^{*}=0.3~m_{e}\) [34] 的各向同性抛物线能量色散。出于同样的原因，我们将 ZnO NCs 视为球形系统。

由于 NC 界面 [6] 处的高导带偏移，电子强烈定位在 ZnO NC 体积内，我们强加所有电子波函数以在 NC 边界处消失 r =R .因此，我们考虑 N 相互作用的电子位于无限球形阱内，其整体电荷中性由正电荷表面分布确保，不会在 NC 内部产生任何场。所考虑系统的有效哈密顿量很简单：

其中 V (r 一 ,r b ) 代表对电子库仑相互作用。它的显式表达式，考虑到 ZnO 材料和周围介质的极化，写成多极展开 [3]，

其中 r <和 r> 分别是两个径向位置中最小的和最大的。 ZnO 和甲苯介电常数被指定为它们的体积值 ε 我 =3.7 和 ε 米 =2.25 [21]，分别。使用这些参数，有效玻尔半径 \(a_{0}=\hbar ^{2} \varepsilon _{i}/m_{e}^{*} e^{2} =0.65\) nm 小于NC半径。

单粒子电子能量，ε 我 , 和包络波函数 ψ 我 满足 LDA Kohn-Sham 方程组，

其中平均场势 V mf 由直接的总和给出，V D (r )，然后交换，V x (r ), 部分,

\(\rho =\sum _{i} |\psi _{i}|^{2}\) 是电子密度。请注意，我们可以像通常那样用更现实的局部密度相关交换相关项替换狄拉克形式中的局部密度相关交换项。我们不这样做，因为激发态的理论构建会自动遵循 RPA 性质的大部分基态相关性。

为简单起见，我们考虑具有封闭电子壳层的球对称电子配置。在这种情况下，单粒子波函数作为径向、角和自旋分量的乘积给出 [35]。因此，索引 i =(n ,l )，其中 n 是径向量子数和 l 角动量一。方程的数值解。 (3) 对于电子数N <130 表明基态电子配置由具有最低径向量子数 n 的占据电子态组成 =1。这些电子态具有无节点径向波函数，并因角动量 l 的值而异 .因此，考虑到自旋简并，这种对称配置的“神奇”电子数是 N =2(l 最大 +1) ² , 其中 l 最大 是最高占据电子态的最大角动量。在图 1 中，我们展示了密度分布 ρ (r ) 对于带有 N 的 NC =18、50、128 个电子。可以看到，随着尺寸的增加，径向密度分布变得越来越窄，并向 NC 界面移动。图1的插图显示了电子径向分布<r的平均电子值的大小依赖性 〉 在 NC 半径 R 上 和比率δ r /R ，其色散 \(\delta r =\sqrt {\langle r^{2} \rangle - {\langle r\rangle }^{2}}\)（可以认为是有效电子壳宽度）到NC 半径。对于具有 N 的最小 NC，该比率仅为 ~ 0.15 对于较大的系统，=8 个电子迅速减少。从数值上看，电子壳的宽度δ r 大约是有效玻尔半径 a 的三分之二 0 而电子壳层的峰由于量子反射而从 NC 界面偏移了大约 R -〈r 〉≃2a 0. 电子系统的这一特征源于强大的库仑排斥力，将电子推向 NC 边界，形成中空的球形电荷分布。如果 NC 半径足够大，则 NC 边界处的库仑排斥力 e ² N /ε 我 R ² 变得远强于离心力 \(\hbar ^{2}l(l+1)/m_{e}^{*}{\langle r \rangle }^{3}\) 即使对于最高占据状态\(l=l_{max}=\sqrt {N/2}-1\)。可以看到它们的比率是 a 0/2R .这就是为什么如果 R 径向和角电子运动分开 ≫a 0. 在这种情况下，电子系统类似于一个量子旋转器，例如，占据单粒子态的能谱ε 我 等式的(3) 由公式很好地逼近，

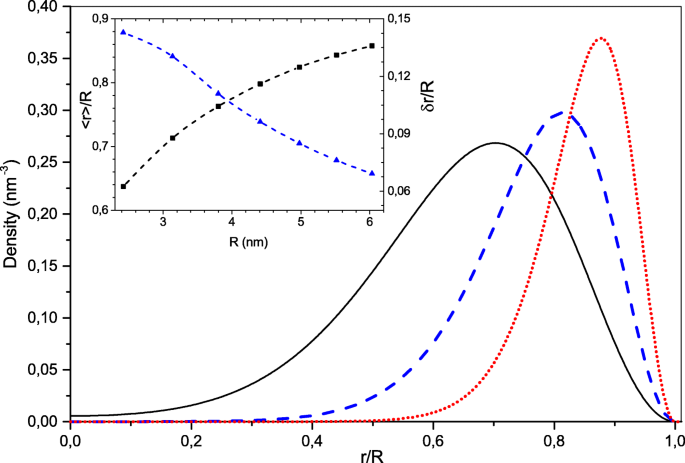
具有不同离域电子数 N 的 NC 的径向密度分布 =18（纯黑色）、50（蓝色虚线）、128（红色虚线）。在插图中，减小的平均半径（黑色）及其离散度（蓝色）表示为 NC 半径的函数

光学响应

在线性响应近似中，外部谐波电场会引起相同频率的时间相关的自洽场。相应的小振幅振动的知识提供了有关偶极子激发态以及基态和激发态之间跃迁概率的信息。对于基态为 Slater 行列式的系统 |Φ 0>，RPA 方法中的相关多体偶极子激发态被构造为粒子-空穴激发的线性叠加[36]：

。 $$ (6)

索引 i ,米 , (j ,n ) 指费米能级 F 以上（以下）的单粒子态； \(\hat {a}^{+}\) 和 \(\hat {a}\) 分别是创建和销毁单粒子算子。

通过求解矩阵 RPA 方程 [ 28]：

$$ \left(\begin{array}{ll} \mathbf{A} &\mathbf{B} \\ \mathbf{B}^{\star} &\mathbf{A}^{\star} \end{数组} \right) \left(\begin{array}{l} \mathbf{X}^{\nu} \\ \mathbf{Y}^{\nu} \end{array} \right) =\omega_{ \nu} \left(\begin{array}{l} \mathbf{X}^{\nu} \\ -\mathbf{Y}^{\nu} \end{array} \right), $$ (7 )

其中特征值 ω ν 是激发能。矩阵A 和 B 定义如下

$$ {\begin{aligned} A_{ij,mn}&\,=\,\delta_{im}\delta_{jn}\left(\varepsilon_{i}-\varepsilon_{j}\right) \,+ \, \left\lange in\left| \hat{v}\right| jm\right\rangle, \quad B_{ij,mn}&\,=\,\left\langle im\left| \hat{v}\right| jn\right\rangle \\ \hat{v}(\mathbf{r},\mathbf{r}^{\prime}) &=V(\mathbf{r},\mathbf{r}^{\prime} )+ \delta\left(\mathbf{r}- \mathbf{r}^{\prime}\right)\delta V_{x}/\delta \rho. \end{对齐}} $$ (8)

请注意，后向幅度 \(Y_{ij}^{\nu }\) 测量电子-空穴基态相关性的贡献 \(\hat {a}_{j}^{+}\hat { a}_{i}|\Phi _{0}>\)，分别为激发态|Φ ν>频率ω ν .

对应的偶极子振子强度f ν 用 RPA 幅度 X 表示 ^ν 和是 ^ν ,

$$ f_{\nu} =\frac{2 m_{e}^{*} D^{2}_{\nu}\omega_{\nu}}{\hbar^{2}}, \quad D_{ \nu} =\sum_{ij} \left(X^{(\nu)}_{ij} d_{ij} + Y^{(\nu)}_{ij} d_{ji} \right), $ $ (9)

其中 d ij =<i |z |j 〉是单粒子偶极矩阵元。

光吸收截面是通过用洛伦兹曲线加宽计算的振子强度分布来获得的，折叠宽度为 0.2 ω .具有 N 的 NC 的光吸收光谱和振子强度分布 =8 (a), 32 (b), 50 (c) 和 128 (d) 个电子如图 2 所示。在图 2d 中，我们将计算出的光吸收截面与参考文献的实验数据进行了比较。 [21] 对于带有 R 的 ZnO NC ≃ 6 纳米。可以看到，在所有考虑的 NC 中，光谱由单个共振线支配，该位置实际上决定了光吸收截面的最大值。事实上，这是可以预料的，因为单粒子电子光谱类似于量子旋转器。最强的跃迁发生在最大波函数重叠时，即具有相等的径向量子数 n .在我们的例子中，从最高占据状态 j 只有一个这样的光学跃迁 =(1,l 最大 ) 到最低空状态 i =(1,l 最大 +1）。然而，每当强库仑排斥使电子相关性变得重要且势不可挡时，相应的偶极子激发与非相互作用的单粒子跃迁有很大不同。 R 就是这种情况 ≫a 0. 即集体激发的能量，ω ν , 超过单粒子跃迁能量

$$ \Delta =\left(\epsilon_{1, l_{max}+1} -\epsilon_{1, l_{max}}\right)=\frac{\hbar^{2} (l_{max}+ 1)}{m_{e}^{*}{\langle r \rangle}^{2}}。 $$ (10) <图片>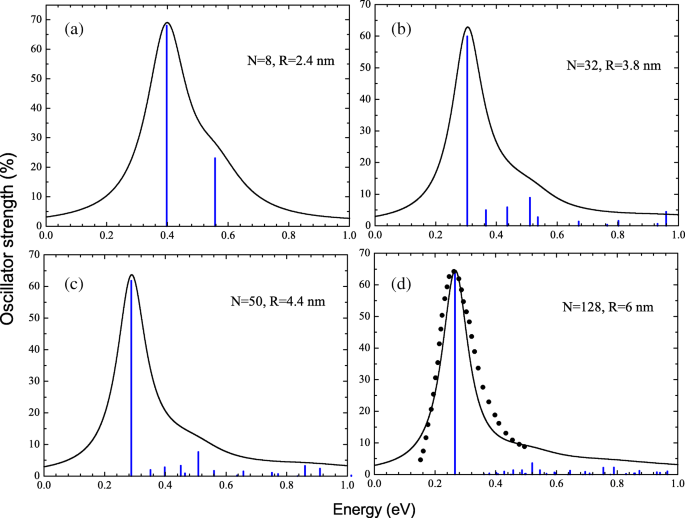

在 RPAE 方法中为具有 N 的 NC 计算的振荡器强度分布和相应的光吸收峰轮廓 =8 (a ), 32 (b ), 50 (c ) 和 128 (d ) 导带电子。 NC 与 R 的实验 [21]（黑色方块）和计算（实线）共振峰轮廓的比较 ≈6 纳米 (d )

在图 3 中，我们比较了光吸收最大值的位置，ω 资源 ，此处计算（蓝色圆圈）与 [21] 的实验结果（红色星星）。人们观察到实验数据与我们的理论结果之间存在显着的一致性。为了比较，我们还在这里绘制了能量 Δ 单粒子跃迁（绿色方块）。与 Δ 相比，电子相关显着增加了集体激发能 . RPA 方程的简单分析。 (7) 解释了这一观察结果。如果我们只考虑来自 j 的主要光学跃迁 =(1,l 最大 ) 到 j =(1,l 最大 +1) 状态，RPA 方程。 (7) 简化为 2×2 矩阵方程，其特征值 ω 很简单：

$$ \omega^{2}=\Delta^{2} +2V\Delta, $$ (11)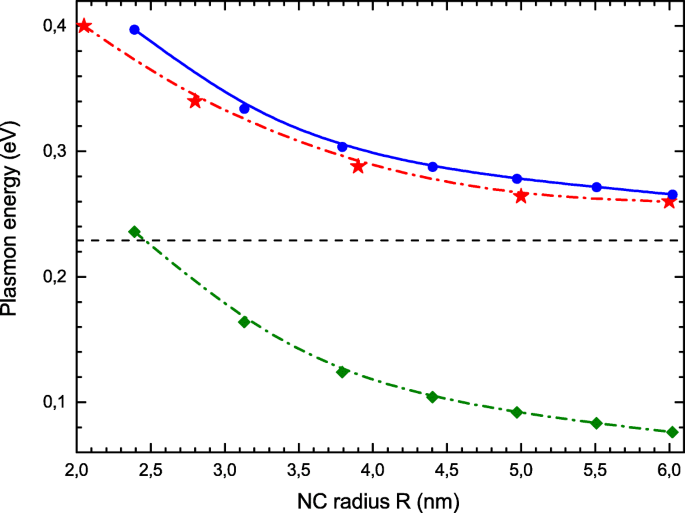

LSPR 能量的大小依赖性。实验值 [21]（红色星星）、具有局部交换的 RPA（蓝色圆圈）、单粒子跃迁能量（下方曲线中的绿色菱形）。水平虚线表示经典值（13）

其中 \(V=\left \langle ij\left | \hat {v}\right | ij\right \rangle \) 表示 RPA 库仑矩阵元素。 r.h.s. 中的第一个术语等式的(11) 给出了单粒子贡献，而第二项来自粒子-空穴相互作用。它们的比值可以通过在表面取电子径向坐标来估计，r =R 在 RPA 矩阵元素 V ，并忽略交换项。这个估计产生

$$ \frac{2V}{\Delta} \simeq \frac{4R\varepsilon_{i}}{a_{0}(\varepsilon_{i}+2\varepsilon_{m})} \simeq \frac{2R} {a_{0}}。 $$ (12)

因此，如果 R ≫a 0.在大NCs的极限下，电子密度分布集中在NC表面；因此，根据方程。 (12)，方程中的共振能量。 (11) 趋于

$$ \omega =\sqrt{\frac{2\hbar^{2}e^{2}N}{m_{e}^{*}(\varepsilon_{i}+2\varepsilon_{m})R^ {3}}}，$$ (13)

这与薄球壳中的经典偶极等离子体频率完全一致 [37]。这种等离子体模式对应于切向电子振动。这样，它类似于C中的表面等离子体共振 60 个分子，其中共振频率由类似于方程的方程很好地描述。 (13) [38]。请注意，与富勒烯情况 [39] 一样，这种等离子体模式聚集了总振荡强度的三分之二（见图 2）。这是因为这种振荡只涉及角自由度，保持径向运动不受干扰。

与众所周知的均匀球体中的偶极子表面等离子体模式相反，它是纯粹的平移，目前考虑的模式是压缩模式。感应密度产生平行于表面的电场，该电场对这种等离子体模式起到恢复力的作用。此外，由于诱导密度振荡引起的局部费米能级的纯量子变化有助于恢复力。对应的量子压力对共振频率的贡献由Δ给出 方程中的术语(11)。由于有效玻尔半径 a 很小，它在所有考虑的 NC 中都小于库仑贡献 0 氧化锌。然而，在具有较大a值的NC中 0, 可以观察到 R 从经典偶极等离子体共振到量子限制机制的转变 ～a 0. 值得注意的是，在掺杂 NCs 的情况下，参数 a 0/R 控制偶极共振的经典/量子性质仅取决于 NC 大小，而不取决于自由载流子的数量 N .

在图 3 中，水平线是指经典的等离子体共振能量 (13)。共振频率相对于其经典值的蓝移是由两种量子效应引起的，即上面讨论的量子压力贡献和平均电子半径的减小。后者的发生是因为电子由于边界的量子反射而被推入 NC 体积，使得 <r 〉≃R −2a 0. 这个效果增加了矩阵元素V 这反过来又增加了共振频率。粗略地说，可以通过替换 NC 半径 R 来重现这种效果 在方程的分母中。 (13) by <r 〉。根据方程。 (11)–(13)，这两种效应都提供了与逆 NC 半径成比例的蓝色频移 ∝1/R .但从数值上看，最后一位的贡献最大。

结论

为了结束这封信，我们已经制定了一个理论，可以很好地预测在高度 n 掺杂的胶体 ZnO NCs 中观察到的强偶极共振。已经使用多体量子方法从理论上研究了新型表面偶极等离子体激发。我们已经证明，光掺杂 ZnO 纳米晶体中的强库仑排斥导致特定的基态电子分布位于靠近内表面的薄表面层中。当偶极子被激发时，这种电子分布会维持集体等离子体振荡，这种振荡基本上由角运动形成。这种表面等离子体模式从经典到量子限制机制的转变由一个参数控制，该参数等于纳米晶体尺寸与有效玻尔半径的比率。来自 NC 界面的电子反射减小了电子壳半径。此外，局部费米能级的变化对等离子体振子恢复力有额外的贡献。这些量子效应导致共振等离子体频率的大小依赖性，这与实验观察结果非常一致。在大NC半径的限制下，共振线平滑地趋向于无限小宽度带电壳的经典等离子体频率。

缩写

LDA：

局部密度近似

LSPR：

局域表面等离子体共振

NC：

纳米晶

RPA：

随机相位逼近