Ti3C2Tx MXene 的原位高压 X 射线衍射和拉曼光谱研究

背景

经过十年对石墨烯 [1] 和过渡金属二硫属化物 (TMD) [2,3,4,5] 的深入研究，二维 (2D) 金属碳化物 (MXenes) 由于其非凡的电气特性 [6, 7]。 Ti3C2 MXene 是一种具有范德华叠层结构的层状材料，其中每层包含夹在三个 Ti 原子平面之间的两个碳原子平面。在Ti3C2 MXene的能带结构中，导带在Γ点接触价带，表明Ti3C2 MXene是半金属材料[8]。更有趣的是，Ti3C2 Mxene 的能带结构可以通过表面官能团（在公式中标注为“T”）[8]，例如–F、–O 和–OH [9] 稍微打开。这些官能团是在 Mn 的溶液蚀刻中产生的 AlCn + 1 相 [9]，然后形成 Ti3C2Tx 具有可调电特性的 MXene。 Ti3C2Tx的电导率 MXene 测量值为 4.2 × 10 ^-4 S/m [10]，优于大多数 TMD。迄今为止，Ti3C2Tx MXenes 已在先进超级电容器 [11]、锂电池 [12]、电磁屏蔽 [10]、抗菌 [13]、 中显示出潜在应用 和发光[14]。

Ti3C2Tx除了具有高导电性外，还具有弹性 MXene 也备受关注。理论计算预测，这种超薄碳化物的杨氏模量高达 ~ 500 GPa [15,16,17]。利帕托夫等人。最近使用纳米压痕来确定单层 Ti3C2Tx 的杨氏模量 MXene 为 330 Gpa [18]。这些值远高于 MoS2 [18] 的值，并且与单层石墨烯 [19] 的值相当。最近，Ghidiu 等人。测量了 Ti3C2Tx 的高压 X 射线衍射 (XRD) 光谱 MXene 高达 3 GPa 并且没有观察到相变 [20]。但是，作为参考中加载的压力。 [20]过低，Ti3C2Tx的相稳定性和晶格变形 在更高的压力下仍然未知。

拉曼光谱作为一种有用的非破坏性工具来研究二维材料（如石墨烯 [21] 和 TMD [2]）的晶体结构和声子振动。 Ti2CTx的组成 [22] 和 Ti3C2Tx 的相稳定性 可以使用共焦拉曼测量来探测不同退火条件下的 Mxene [10]。最近，Ti3C2Tx 的声子色散 MXene 由 Hu 等人 理论计算。 [23, 24]，从而能够进一步了解这种材料的拉曼光谱。然而，Ti3C2Tx 的高压拉曼光谱 仍然缺乏。此外，Ti3C2Tx 的声子响应 作为压力的函数未知。

在本文中，我们制备了 Ti3C2Tx 薄片并测量了它们与压力相关的 XRD 和拉曼光谱，最高可达 26.7 GPa。 Ti3C2Tx的弹性常数 由 Murnaghan 方程从 XRD 衍射峰位移计算。面外声子的正 Grüneisen 参数是从它们的压力相关拉曼位移和晶格参数变形比中获得的。所得结果将有助于进一步了解 Ti3C2Tx 的力学和声子振动行为 MXene。

结果和讨论

在进行高压测量之前，我们首先研究了剥离的 Ti3C2Tx 的基本材料特性 Mxene 薄片。剥离的 Ti3C2Tx 的光学图像 沉积在 Si/SiO2 (300 nm) 衬底上的薄片如图 1a 所示。对于剥落的薄片，可以观察到浅绿色对比。正如 Miranda 等人报道的那样，Ti3C2Tx 的光学对比度 薄片强烈依赖于薄片厚度，较厚的薄片总是显示出更高的对比度，而薄的薄片则显示出低对比度 [25]。图 1b 中大多数薄片的浅绿色对比表明它们的厚度很薄。剥离的 Ti3C2Tx 的原子力显微镜 (AFM) 形貌图像 薄片如图 1b 所示。映射区域中的薄片显示出具有高粗糙度的表面，这是 Ti3C2Tx 的典型特征 片 [26]。典型薄片的厚度可以从其穿过图 1b 中标记位置的线轮廓（图 1b 的插图）确定为 170 纳米。剥落薄片的扫描电子显微镜 (SEM) 图像如图 1c 所示。 Ti3C2Tx的层状结构 可以清楚地看到，表明成功制备了 Ti3C2Tx 分层样本[10]。

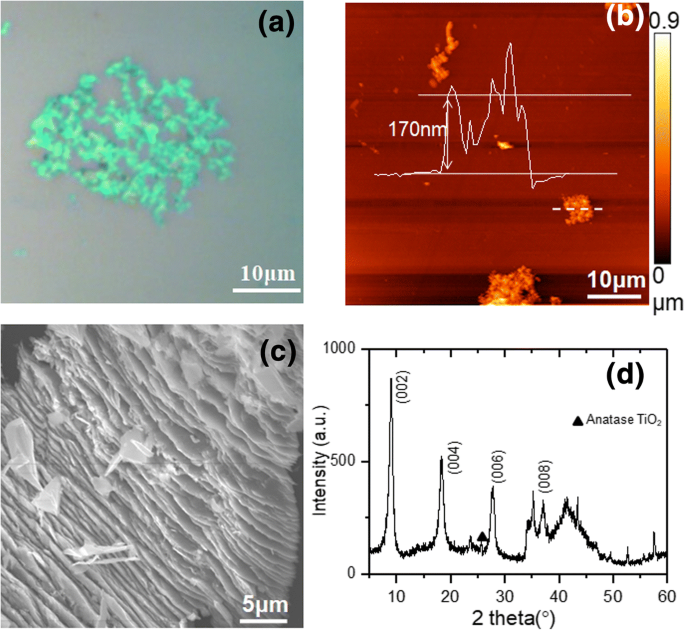
一 超声剥离的 Ti3C2Tx 的光学图像 薄片; b 超声剥离的 Ti3C2Tx 的 AFM 形貌图 薄片，穿过标记虚线的线轮廓显示为插图，表示 Ti3C2Tx 170 nm 的薄片厚度； c 超声剥离的 Ti3C2Tx 的 SEM 图像 薄片; d Ti3C2Tx的XRD谱 原粉

我们进一步测量了原始 Ti3C2Tx 的 XRD 谱 粉末，如图 1d 所示。此 XRD 模式类似于以前的报告 [10]；因此，在 8.95°、18.28° 和 27.7° 处的突出峰可以归因于 (002)、(004) 和 (006) 面的衍射。与突出峰相比，次要相（锐钛矿TiO2（101）在25.3°，JCPDS Card No.71-1116）的衍射峰强度相对较弱，表明Ti3C2Tx的纯度较高 所得粉末中的相。 (002) 峰出现的角度略低于 Han 等人报道的角度。 (9.21°) [10]。计算出的 c 晶格参数 19.66 Å 大于报告值 (19.2 Å) [10]。应该注意的是，由于层间空间可以通过不同密度的化学基团和离子进行调整，例如-F、-OH 和 Li ⁺ ，c 在不同的研究中，晶格参数在 19.2 Å 到 58.8 Å 之间变化很大 [10, 20, 26, 27]。 c 我们样品的晶格参数非常接近 Ti3C2Tx 测量的低值 仅使用 HF 作为蚀刻剂的粉末 [10]。

Ti3C2Tx的XRD谱 在不同压力下测量到 26.7 GPa 的薄片如图 2a 所示。可以看出，在不同压力下测得的光谱彼此相似，但没有发现新的衍射峰。这一发现表明压力高达 26.7 GPa 时没有发生相变。在图 2a 中，随着压力的增加，所有的衍射峰都向大角度移动，表明 Ti3C2Tx 的收缩 格子。 Ti3C2Tx 也观察到了这种伪负压缩性 [20] 和其他具有层状结构的低维材料，如石墨 [28]、氧化石墨烯 [29, 30]、二硫化钼 [31]、粘土 [32] 和钛酸盐 [33]。随着压力从 1.8 GPa 增加到 26.7 GPa，(002) 峰从 2.883° 移至 3.162°。晶格参数c的变形率 , c /c 0 ，作为压力的函数，可以从 (002) 峰的位移计算。此外，a的变形率 , a /a 0 , 可以从 (110) 峰的位移计算。如图 2b 所示，晶格参数 c 和 a 在 26.7 GPa 的压力下，它们分别变形了 9.1% 和 2.4%。在~ 3 GPa的低压区，晶格参数c的压缩比 是 3%。在之前对 Ti3C2Tx 的高压 XRD 测量中 薄片，稍大的 c 干燥 Ti3C2Tx 的压缩比为 4% Ghidiu 等人报道了薄片。 [11]（图 2b）。这种差异可能是由较大的晶格参数 c 引起的 (25.1 Å) Ghidiu 等人使用的样品。 [11] 相对于我们的 (19.66 Å)。

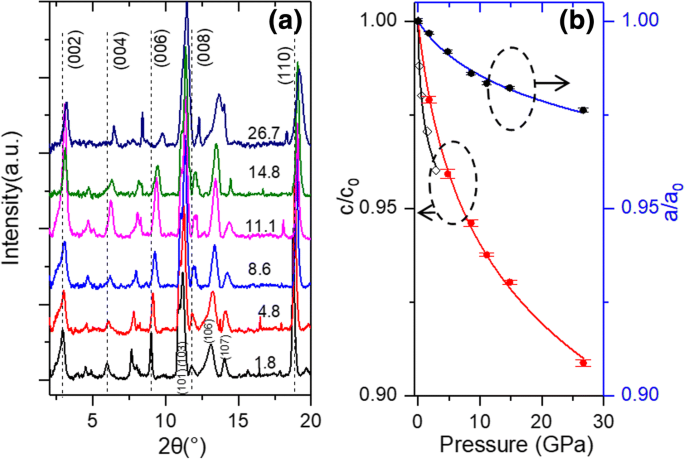
一 Ti3C2Tx的XRD谱 在不同的负载压力下。请注意，每个光谱上标注的压力的单位是 GPa。根据参考分配峰值。 [26]; b 实验（点）和计算的压缩比（实线）沿 c 和 a 方向。实线是使用方程 \( r(P)/{r}_0={\left[\left({\delta}_0/{\delta}^{\prime}\right)P+1 \right]}^{\delta^{\prime }} \)

为了获得弹性常数，c 和 a 图 2b 中的压缩比通过使用 Murnaghan 方程 [34] 进一步拟合。

其中 r 表示沿 c 的晶格常数 和 a 轴，\( {\beta}_0^{-1}=-{\left(\frac{dlnr}{lnP}\right)}_{P=0} \) 是线性压缩率，而 β ^′ 是 β 的压力导数 .

适合的 r /r 0 a 的曲线 和 c 在图 2b 中绘制为实线。可以看出，实验结果非常符合方程的期望。最佳拟合生成 β 0 和 β ^′ 对于 c 分别为 67.7 GPa 和 25.5。而对于晶格参数a , β 0 和 β ^′ 分别计算为 387.4 GPa 和 72.1（表 1）。对于石墨烯等超薄二维材料，杨氏模量 (1TPa) 非常接近 β 0 厚石墨 [19, 28]。因此，β 0 可以作为替代来评估 Ti3C2Tx 的弹性常数 . Ti3C2Tx 的杨氏模量 最近由 Lipatov 等人测量。为 330 GPa [18]，与 β 一致 0 在我们的研究中。我们的测量值也与其他研究中计算的 Ti3C2 的弹性常数相当 [15, 17]（表 1）。 β 0 在 c 轴比石墨大（β 0 = 35.7 GPa)，而 β 0 在 a 轴比石墨小（β 0 = 1250 GPa) [28]。 β 0 Ti3C2Tx 高于 MoS2 (270 Pa) [35] 的体积模量，也与氧化石墨烯 (210 GPa) [36] 相当，表明 Ti3C2Tx 具有高弹性常数 二维材料中的Mxene。

Ti3C2Tx的高压拉曼光谱 在高达 25.5 GPa 的不同压缩压力下测量样品，如图 3a 所示。在不同减压压力下获得的拉曼光谱如图 3b 所示。在低压缩压力下，Ti3C2Tx Mxene 在 ~ 210、~ 500 和 700 cm ⁻¹ 处表现出三个主要的拉曼谱带 .需要注意的是 Ti3C2Tx 的拉曼光谱 MXene 在不同类型的文献中差异很大。胡等人。 [23] 报告了在 ~ 200 cm ⁻¹ 处的强拉曼峰 和 720 cm ⁻¹ , 而其他波段在 400 cm ⁻¹ 相当广泛。然而，韩等人。 [10] 和朱等人。 [37] 在 ~ 200 cm ⁻¹ 处观察到一个尖峰 ，但其他乐队都很广泛。薛等人。 [14] 仅观察到 100 到 700 cm ^-1 的宽峰 .图 3 中的拉曼光谱与参考文献中的不同。 [10, 14, 23, 37]。这种差异可能是由 Ti3C2Tx 上不同类型和浓度的化学基团引起的 MXene。对这些不同拉曼谱带的进一步解释需要回忆 Ti3C2Tx 的声子色散 这是胡等人在理论上计算出来的。 [23, 24]。 Ti3C2Tx的空间群 是 P63/mmc [23]。原子数 (N ) 在 Ti3C2Tx 的原始细胞中 给定 x，对于 T =-O、-F 和 -OH，分别计算为 7、7 和 9 =2. 在 Γ 在第一布里渊区的点，预测不同 Ti3C2Tx 存在以下光学声子 MXenes：Γ 光学 (Ti3C2O2) =6E g + 3A 1g , Γ 光学 (Ti3C2F2, Ti3C2 (OH)2) =8E g + 4A 1g [23]。 Ti3C2F2 和 Ti3C2(OH)2 不同拉曼活性模式的原子振动如图 2 所示。它们的频率由 Hu 等人理论计算。 [23] 并列在表 2 中。对于 Ti3C2(OH)2，有四种面外模式 (A 1g ：218、514、684 和 3734 厘米 ⁻¹ ) 和四种面内模式 (E g ：138、278、437 和 622 厘米 ⁻¹ ）。对于 Ti3C2F2，有 3 个 A 1g 模式（190、465 和 694 cm ^{− 1} ) 和三个 E g 模式（128、231 和 612 cm ^{− 1} ) [23]。

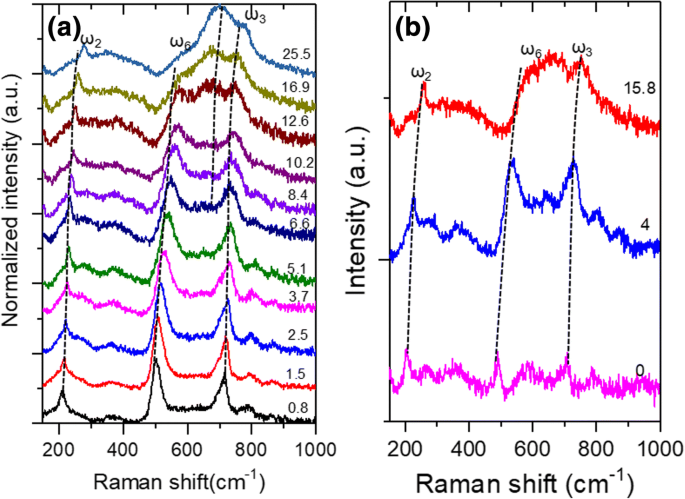
一 Ti3C2Tx的拉曼光谱 不同压缩压力下的薄片； b 在不同减压压力下获得的拉曼光谱。注意a中的压力单位 和 b 是 GPa

然而，可以看出，纯 Ti3C2F2 或 Ti3C2(OH)2 的计算声子频率不能拟合 Ti3C2Tx 的实验拉曼光谱 在图 3. 因为 Ti3C2Tx 的表面 通常由不同类型的化学基团连接，图 3 中实验拉曼光谱的完整解释需要考虑 -F 和 -OH 的混合振动模式 [23]。在之前的研究 [23] 中，拉曼谱带在 ~ 200、~ 500 和 ~ 700 cm ⁻¹ 分别分配给 ω2、ω6 和 ω3。按照此说明，在 205.6、490.2 和 702.5 cm ⁻¹ 处的显着拉曼谱带 图 3a、b 可以分别分配给 ω2、ω6 和 ω3 模式。有趣的是，这些模式都是面外模式。其他拉曼模式由于强度低而难以与其相邻模式隔离。为了通过消除不确定性获得稳健的数据，以下计算和分析仅考虑这三种模式。

在图 3a、b 中，还可以看出这些面内模式的相对强度随着压缩压力的增加而增加（图 3a）。当压缩压力≥ 12.6 GPa时，在~ 600 cm ⁻¹ 处出现新峰 (ω4) 出现并成为突出峰值。在减压过程中，这种ω4模式的强度显着降低。在 0GPa 减压压力下获得的拉曼光谱包含几乎所有的面内和面外声子模式。这种在高压缩压力下出现的面内模式可能与薄片断裂或取向旋转引起的极化有关。关于这种影响的研究仍在进行中，将在未来报告。

随着压力从 0.8 GPa 增加到 25.6 GPa，ω2、ω6 和 ω3 都显示出单调增加的蓝移（图 4a-d），这类似于石墨 [28] 和 MoS2 [31] 的压力相关蓝移。在 25.6 GPa 时，这三种模式的蓝移分别为 66.7、85.1 和 60 cm ⁻¹ ， 分别。这种与压力相关的蓝移比 MoS2 的蓝移大得多 [31]。为了量化拉曼位移与压力的关系，图 4a、b、d 中的拉曼位移图使用以下等式 [28] 拟合：

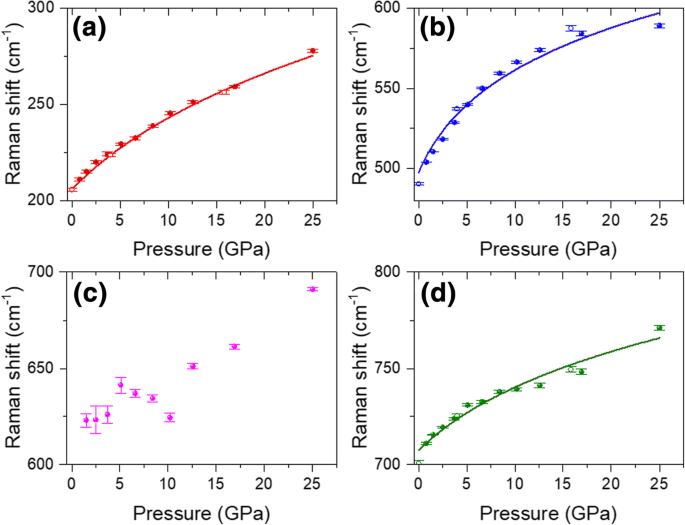
作为不同压缩压力（实心球体）和减压压力（空心圆）的函数的不同声子模式的拉曼位移：a 210 厘米 ⁻¹ , b 504 厘米 ⁻¹ , c 620 厘米 ⁻¹ , 和 d 711 厘米 ⁻¹ .实线是使用方程 \( \omega (P)/{\omega}_0={\left[\left({\delta}_0/{\delta}^{\prime}\right)P+ 1\right]}^{\delta^{\prime }} \)

其中 δ 0 和 δ ^′ 是对数压力导数(dlnω /dP )P =0 和 dlnω 的压力导数 /dP ， 分别。拟合结果在图 4a、b、d 中绘制为实线。由于低压区的高度不确定性，620 cm ^-1 处的拉曼模式 没有安装。从图 4a、b、d 中可以看出拟合曲线与实验结果一致，表明拟合过程的准确性较高。得到的δ参数 0 和 δ ^′ 列在表 3 中。

对于具有原子厚度的各向异性二维材料，例如 MXene 和石墨烯，Grüneisen 张量的两个独立分量通常与平行和垂直于 c 的应变相关 轴。为简单起见，我们采用了 Zallen 等人提出的缩放关系。 [38]，它已被 Hanfland 等人用于拟合石墨的压力相关拉曼位移。 [28]

其中 r 分别是指层内和层间模式的面内和面外晶格常数。 γ 等价于其他研究中定义的 Grüneisen 参数 [39, 40]。

由于在压缩过程中只观察到面外模式，c 作为静水压力函数的晶格参数足以进行计算。我们采用图 2b 中 (002) 平面 0 到 26.7 GPa 的空间距离数据来计算 Grüneisen 参数 γ . ω2、ω6 和 ω3 的平均 \( \overline{\upgamma} \) 高达 26.7 GPa 分别计算为 1.08、1.16 和 0.29（表 2）。与石墨类似，与其他两种模式相比，ω3 的较小 \( \overline{\upgamma} \) 表明刚性层运动中的力常数变化较小 [28]。据我们所知，Ti3C2Tx 的 Grüneisen 参数 还没有被报道。但是，我们仍然可以将我们的数据与其他 2D 材料进行比较。查等人。据报道，Ti2CO2 的声学声子模式的 Grüneisen 参数为 4-5 [41]。由于高频光模的 Grüneisen 参数通常比低频模的 Grüneisen 参数低一到两个数量级 [28]，因此 Ti2CO2 光声子的 Grüneisen 参数可以估计为 0.05-0.5，类似于我们对 Ti3C2Tx 的价值观 .最近，彭等人。 [42] 报道了室温下 MoS2、MoSe2 和 WS2 的 Grüneisen 参数分别为 1.22、1.20 和 1.15，比我们的结果大。我们的结果也小于石墨烯的结果（E 为 1.99 2g 模式）[40] 和石墨（E 为 1.06 2g 模式）[28]。这一发现表明 Ti3C2Tx MXene在这些超薄二维材料中键合非谐性最弱[42]。

结论

总之，我们测量了 Ti3C2Tx 的晶格变形和声子响应 不同静水压力下的薄片，最高可达 26.7 GPa。在低于 26.7 GPa 的压力下未观察到相变。随着压力的增加，所有声子模式都显示出正频移。三个面外声子的正 Grüneisen 参数计算为 1.08、1.16 和 0.29。我们的结果增加了对 Ti3C2Tx 的机械和热性能的理解 在高压下。

方法

Ti3C2Tx 采用参考文献[43]报道的方法制备粉末。简而言之，Ti3AlC2 粉末（Forsman，10g）在室温下通过 HF 溶液（160ml）蚀刻 5 小时。得到的Ti3C2Tx 将粉末分散到去离子水中并以 700 W 的功率超声剥离。所得溶液在储存 24 小时后分离。获得的上层溶液用于进一步的拉曼、原子力显微镜 (AFM) 和扫描电子显微镜 (SEM) 分析。使用 X 射线衍射仪（Rigaku，MiniFlex600）测量环境压力下的 X 射线衍射（XRD）光谱。使用扫描电子显微镜（Hitachi，Su1510）获得 SEM 图像。原位高压 XRD 测量是在上海同步辐射装置中通过垫片高压金刚石砧座 (DAC) 在室温下进行的。为了在样品周围产生静水环境，我们使用甲醇/乙醇/水 (16:3:1) 作为压力传递介质。压力由锐利的红宝石荧光 R1 谱线的压力相关光谱位移确定。将样品放置在带有金刚石尖底（直径 400 微米）的不锈钢垫圈孔（直径 100 微米）中。高压拉曼散射测量使用雷尼绍 inVia 拉曼光谱仪进行，激发波长为 532 nm。地形测量在 AFM 仪器 (Bruker, Innova) 上进行。

衍射峰位置和拉曼峰位移的拟合在 OriginPro 软件包上进行。一个用户定义的函数，y =(A1 × x + 1) ^A2 , 通过设置 A1 和 A2 作为拟合参数来使用。用单纯形法很容易得到合适的拟合。

缩写

二维：

二维

原子力显微镜：

原子力显微镜

DAC：

金刚石砧座

SEM：

扫描电子显微镜

TMD：

过渡金属二硫属化物

XRD：

X射线衍射