应变对 InSe 单层热电性能的影响

介绍

自从发现石墨烯以来，二维 (2D) 半导体材料一直吸引着研究人员的注意力，以探索其迷人的特性和有用的应用。特别是，二维金属硫属化物家族因其非凡的电子、光学和机械性能而在纳米电子学和纳米光子学中显示出巨大的潜力 [1,2,3,4]。最近，硒化铟 (InSe)，一种 III-VI 族层状金属硫属化物化合物，在实验和理论上都引起了极大的兴趣。据报道，InSe 的原子层通过物理 [5,6,7,8,9,10] 和化学方法 [11,12,13,14] 成功合成，以及 InSe 纳米片在传感器上的应用 [15] 、光电子学和光电探测器已被探索。斯里尼瓦萨等人。报道了制造具有高响应度和从可见光到近红外区域的宽光谱检测的少层 InSe 光电探测器 [6]。班杜林等人。在少层 InSe 中发现了高质量的二维电子气，载流子迁移率为 10 ³ 和 10 ⁴ 厘米 ² /Vs 在室温和液氦温度下 [16]。魏等人。发现的背栅多层 InSe FET 具有高达 1055 cm ² 的超高载流子迁移率 /Vs 在室温下由于抑制了来自介电基板的载流子散射 [5]。

二维 InSe 具有相当不寻常的能带结构，它是价带顶部的平坦带和导带底部的抛物线带的组合，因此表现出很高的热电特性[17]。特别是，热电性能可以用无量纲的品质因数来描述，ZT , 定义为 ZT =S ² Tσ/ (Κ e + Κ l)，其中S 是塞贝克效率，T 是绝对温度，σ 是电导率，Κ e 和 Κ l 分别是电子载流子和晶格贡献的热导率。晶格热导率K l 与声子传输特性相关的温度对确定热电性能起着重要作用。之前报道的K InSe 单层的 l 远低于石墨烯，而是 SnSe 片的 10 倍 [18, 19]。

高水平的电子迁移率和低热导率有利于热电性能。此外，单层 InSe 表现出优异的机械柔韧性，并且电子特性可以在很宽的范围内通过中等应变进行连续调制 [20,21,22]。已经证明，通过压缩应变下的能带收敛可以显着提高单层 InSe 的热电功率因数 [23]。对于热电材料，拉伸应变也会引起能带结构和热传输特性的变化。然而，热传输特性对应变的依赖性是不可预测的，与特定的材料和晶体结构密切相关。在本文中，目前的工作是通过第一性原理计算，包括电子和声子传输特性，对 InSe 单层热电性能的双轴拉伸应变效应进行了研究。由于非谐波散射的增加，确定了拉伸应变对 InSe 单层热电性能的积极影响。

方法论

InSe 单层的结构和电子特性的计算是基于密度泛函理论 (DFT) 执行的，如在 Vienna ab initio 模拟包 (VASP) [24,25,26] 中实施的。我们选择了具有局部密度近似 (LDA) [27,28,29] 的投影仪增强波方法作为交换相关函数。和沿 z 的 12 Å 真空 -axis 用于避免板坯周期性图像之间的相互作用。 21 × 21 × 1 和 31 × 31 × 1 Monkhorst-Pack k 网格用于晶胞的结构松弛和电子结构计算。平面波基的能量截止设置为 500 eV。总能量的收敛准则设为10 ^-4 eV，所有原子位置和晶格结构完全松弛，力容差为10 ^-3 eV/Å。

热电传输特性可以通过在 BoltzTraP 程序中实现的 Boltzmann 理论在恒定弛豫时间近似内获得 [30, 31]。在这个近似值内，电子输运系数可以由下式给出

其中Ω是晶胞的体积，f μ 是费米-狄拉克分布函数，α 和 β 是张量指数。传输分布函数 ∑αβ (ε ) 由

其中 N 0表示q的个数 采样点，i 是波段索引，v 是载流子的群速度，τ 是放松时间。

ShengBTE 包 [32] 用于求解声子 Boltzmann 传输方程并确定晶格热和其他相关参数。通过使用密度泛函微扰理论 (DFPT) 计算 [33]，使用 5 × 5 × 1 超胞来计算谐波原子间力常数。并使用有限差分方法计算具有 4 × 4 × 1 超胞的非谐原子间力常数 [34]。使用Phonopy程序计算声子谱[35]。

结果与讨论

单层 InSe 是一个四重原子片，在一层中具有 Se-In-In-Se 共价键。从顶视图看，单层呈蜂窝状晶格，每个 Se 原子与其他三个 In 原子键合，如图 1a 所示。在总能量最小的基础上，计算出该晶体的晶格参数为a 0 =3.95 埃。在本文中，我们在单层 InSe 上采用双轴应变，通过将其晶格改变为 δ 来保持晶体对称性 =(a -a 0)/a 0 × 100%，其中 a 和 a 0 分别是有应变和无应变的单层 InSe 的晶格常数。当对单层 InSe 施加双轴拉伸应变时，键长 d InSe随着应变的增加单调增加，这导致In-Se-In键角增加（见图1b）。

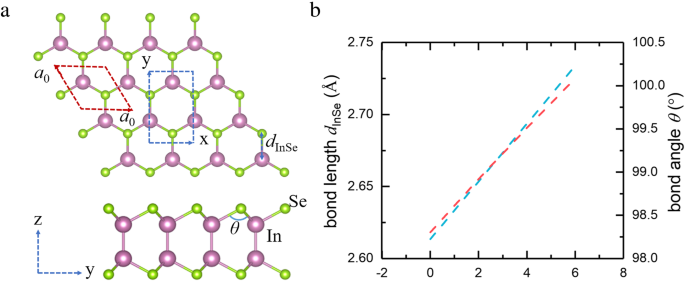
一 单层 InSe 的顶视图和侧视图。粉色和绿色球分别代表 In 和 Se 原子。 b 键长和键角随双轴拉伸应变的增加而变化。基本的a 0 × a 0 单元格和 x × y InSe单层的超胞分别用红色和蓝色虚线表示

InSe单层表现出带隙为1.67 eV的间接半导体，其中导带最小值（CBM）存在于Г点，价带最大值（VBM）位于Г和K点之间，如图2a所示。 InSe 单层的价带表现出墨西哥帽色散，这也可以在许多二维材料中找到 [36,37,38,39]。在图 2 中研究了响应拉伸应变的能带结构修改，三个导带极值分别由符号 I、II 和 III 表示。在拉伸应变下，能量最低的导带对应变敏感并向下移动，而价带几乎保持不变，导致带隙减小。在没有应变的情况下，第二和第三导带最小值之间存在微小差异，并且带谷趋于收敛。但随着拉伸应变的增加，能量差逐渐增大。我们还比较了不同应变下的带隙与相关理论和实验结果，详见附加文件 1：表 S2。

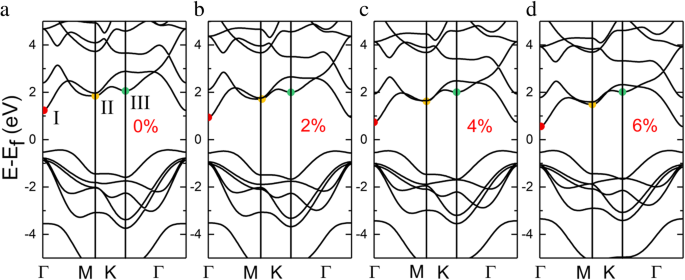
不同应变条件下InSe单层的能带结构

拉伸应变对热电传输系数的影响

在计算出的电子结构的基础上，我们通过半经典玻尔兹曼理论进行热电传输系数计算。关于散射时间τ , 塞贝克系数S , 和电导率 σ 可以计算。图 3a 显示了计算的塞贝克系数作为费米能级的函数。为简单起见，通常假设能带结构在有限温度下掺杂后保持不变 [40, 41]，并且可以通过费米能级位置的变化来获得掺杂对热电传输系数的影响。负 ε f 表示通过将费米能级移入价带的 p 型掺杂，可以获得正的塞贝克系数。类似地，一个正的 ε f 给出负的塞贝克系数。我们可以发现在没有应变的情况下得到的结果与之前的报道非常接近[17]，塞贝克系数的最大值随着拉伸应变的增加而减小，这与带隙的变化有关[42]。

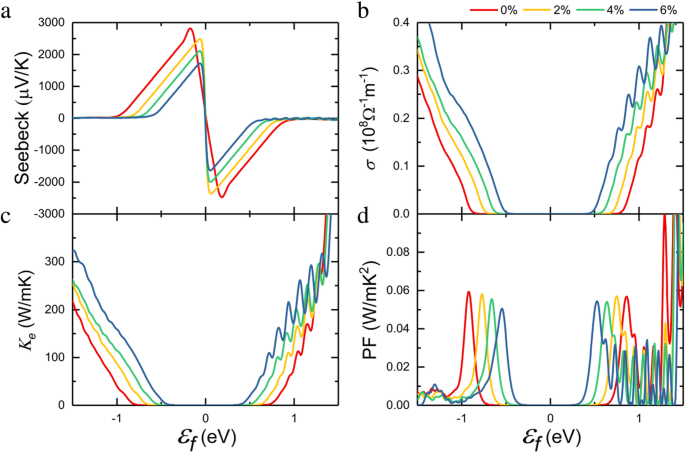
一 塞贝克系数，b 电导率，c 电子热导率，d 施加不同双轴应变时单层InSe的功率因数与300 K化学势的函数关系

计算电导率σ , 弛豫时间 τ 是必需的，因为输出是 σ /τ 在 BoltzTraP 代码中。其中，τ 由

其中 μ 是载流子迁移率和 m * 是有效质量。在形变势理论中，二维材料中的载流子迁移率可由[43, 44]

在这里，e 是电子电荷，ℏ 是普朗克常数，k B 是玻尔兹曼常数。 C 表示弹性模量，可以通过C计算 =(∂ ² E /∂δ ² )/S 0，其中 E , δ , 和 S 0 分别是二维系统的总能量、施加的应变和平衡面积。 E 1是变形势常数，表示为E 1 =ΔE 边缘/Δδ , 其中 ΔE edge 是能带边缘的能量变化。 米 d 是从 \( {m}_d=\sqrt{m_x^{\ast }{m}_y^{\ast }} \) 导出的平均有效质量。为了计算迁移率，矩形 x × y 采用超级单元，如图 1a 所示。获得的C值 沿着 x (y ) 方向为 60.43 N/m (53.68 N/m)，这是通过拟合能应变关系曲线得到的，如附加文件 1：图 S1。计算的变形势E 1 是沿 x 的电子为 6.13 eV (6.14 eV) (y ) 方向，沿 x 的孔为 3.45 eV (3.33 eV) (y ） 方向。单层InSe在不同应变下的有效质量、载流子迁移率和弛豫时间的计算结果总结在表1中。我们可以发现随着方向的不同差异不大，载流子有效质量和迁移率一般是各向同性的。因此，我们使用 x 的平均值 和 y 稍后评估热电性能的方向。施加的应变增强了空穴有效质量，而电子的有效质量几乎保持不变。通过计算出的弛豫时间，可以在图 3b 中的给定化学势下获得电导率。可见电导率σ 由于空穴迁移率的提高，在重 p 型掺杂系统中随着拉伸应变的增加而增加，而 σ 在低掺杂水平下保持相对较低。此外，通过Wiedemann-Franz定律，电子热导率的趋势与电导率保持一致：K e =LσT 在图 3c 中，其中 L 是洛伦兹数。功率因数可由PF =S求出 ² σ /τ ，这决定了可以产生多少电力。考虑到塞贝克系数和电导率的综合趋势，拉伸应变略微降低了功率因数，如图3d所示。

拉伸应变对 Κ 的影响

在金属中，电子是热载体，而在掺杂和温度不是很高的半导体和介电固体中，晶格振动将是能量传输的主要原因 [45]。晶格热导率是热电应用的一个非常重要的参数。从理论的角度来看，作为一个简单的近似值，晶格热导率 Κ l 可以表示为[46,47,48]：

其中 C λ, v λ 和 V 分别是比热贡献、声子群速度和晶体体积。 τ λ是模式λ的弛豫时间，可以使用Matthiessen规则[49]估计：

其中\( \frac{1}{\tau_{\uplambda}^b} \)是边界散射率，\( \frac{1}{\tau_{\uplambda}^{\mathrm{iso}}} \ ) 为各向同性杂质散射率，\( \kern0.1em \frac{1}{\tau_{\uplambda}^{3\mathrm{ph}}} \) 为三声子散射率。

图 4a 表示 Κ l 不同应变下单层InSe随温度的变化。室温下无​​应变情况下的晶格热导率为 25.9 W/mK，与之前的报告 [19] 相当。当施加的应变增加到 6% 时，晶格热导率下降到 13.1 W/mK，这证实了应变工程是一种非常有效的修改晶格热导率的方法。我们在图 4c 中绘制了不同应变下 InSe 单层的相应声子色散曲线，以确定晶格热导率降低的起源。它包含 12 种声子模式，因为单层 InSe 具有四原子晶胞。声子光谱中没有负频率，证实 InSe 单层是热稳定的。声子色散曲线低能区从0开始的三个分支是z 轴声学 (ZA)、纵向声学 (LA) 和横向声学 (TA) 分别为，其他为光学模式。随着拉伸应变的增加，ZA模式的二次性质在低能区变为几乎一条直线。在拉伸应变下可以观察到光学模式频率的下降趋势，因为拉伸应变削弱了键合，然后导致频率降低。我们还讨论了每个声子分支对 Κ 的贡献 l 用于图 4b 中未应变和 6% 应变的单层 InSe。在无应变条件下，ZA 模式对携带热量有显着贡献，当对单层 InSe 施加 6% 的拉伸应变时，ZA 模式的相对贡献从 58% 降低到 38%。随着拉伸应变的增加，ZA模式变得更硬，导致对Κ的贡献减少 l .

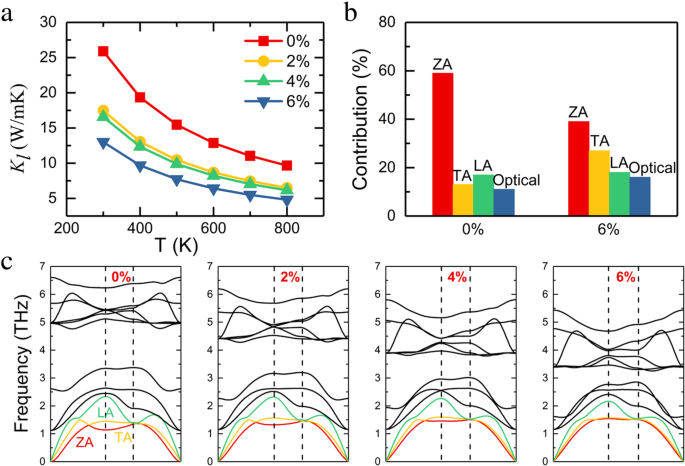
一 计算双轴应变对不同温度下晶格热导率的影响。 b ZA、TA、LA 和所有光学分支对无应变和 6% 应变系统的晶格热导率的贡献。 c 不同菌株下单层InSe的声子色散曲线

接下来，详细分析由拉伸应变引起的声子群速度变化，以了解声子传输特性。对于面内声学模式，声子群速度在应变为 6% 时降低，如图 5a、b 所示。结合 LA 和 TA 的增强贡献，声子群速度的降低在 Κ 的减少中起着至关重要的作用 湖声子群速度的变化源于应变引起的结构变化：当打开拉伸应变时，键距增加，键强度降低，导致声子频率和群速度降低。考虑到三个声子分支对Κ的贡献最大 l、光分支声子群速度的增加作用有限。

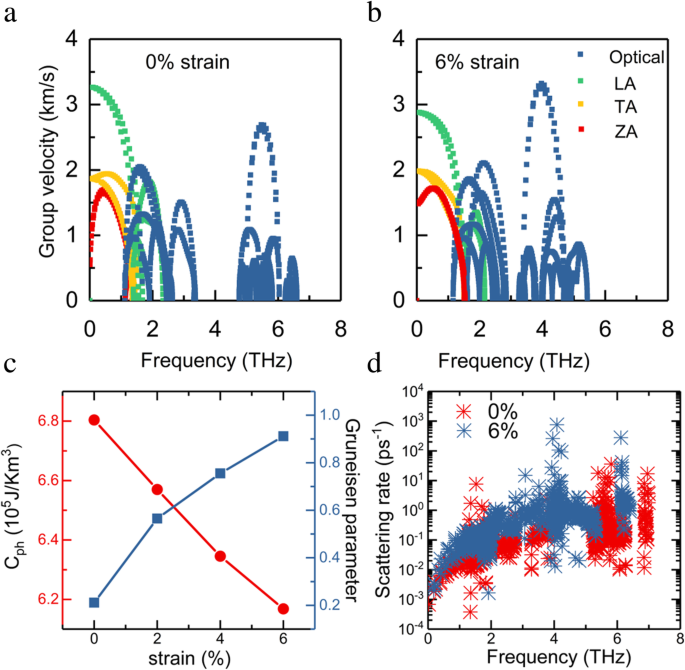
ZA、TA、LA 和光学模式对 (a 的单层 InSe 群速度的贡献 ) 无拘无束和 (b ) 6% 应变系统。 c 声子热容 (C ph) 和 Gruneisen 参数作为 300 K 应变的函数。d 未应变和 6% 应变单层 InSe 的声子散射率与频率的函数关系。

没有和有 6% 应变的单层 InSe 的三声子散射率作为频率的函数如图 5d 所示。可以观察到，6% 应变单层 InSe 在低频区域的三声子散射率明显大于未应变情况，这表明应变的增加导致更强的三声子散射。增强的三声子散射主要是降低晶格热导率的原因，这也与之前的结论一致 [19]。在 ZrS2 和 2H MoTe2 单层中观察到声子散射率随拉伸应变增加的类似趋势 [50, 51]。我们还分析了双轴拉伸应变对声子热容 (C ph )，如图 5c 所示。随着拉伸应变的增加，InSe单层的声子热容单调降低。对于 6% 应变系统，声子热容降低到 6.2 × 10 ⁵ 焦/公里 ³ .由于 ZA 模式的线性化和硬化，声子态密度降低，导致声子热容降低。 Gruneisen 参数提供有关系统非谐性的信息，可以从非谐原子间力常数 (IFC) [32, 52] 中获得。图 5c 显示了不同应变下计算的 Gruneisen 参数。由拉伸应变引起的 Gruneisen 参数增加意味着更强的非谐性，导致较低的热导率 [18]。

利用所有可用的热电传输特性，可以获得品质因数 ZT。施加的拉伸应变对这些传输特性有不同的影响，InSe单层热电性能的改善需要这些参数之间的复杂平衡S , σ , 和 κ .图 6 显示了不同应变下计算的品质因数作为 300 K 下化学势的函数，很明显，不同应变下 ZT 值的变化强烈依赖于化学势，ZT 最大值可以有效地提高应变的增加。在没有应变的情况下，InSe 单层在室温下的峰值 ZT 值为 0.36，接近于硅烯 (0.36)、锗烯 (0.41) 和单层 MoS2 (0.58) [53, 54]，并且低于2D 单硫属化物（700 K 时为 1.29~2.63）[55]。考虑到高载流子迁移率和优异的机械柔韧性，应变 InSe 单层也是一种很有前途的热电应用潜在材料。当施加拉伸应变时，减弱的原子间键会引起更强的非谐性。增加的声子散射率、降低的声子群速度和声子热容共同导致晶格热导率降低，从而导致品质因数提高。先前的理论计算表明，InSe 单层可以承受超过 20% 的拉伸应变，这远大于我们预测的应变 [20]。在实验中，对二维材料施加应变主要是通过它们与基板的相互作用，这可以通过加热 [56]、外延薄膜之间的晶格失配 [57] 或基板上二维材料的弯曲 [58， 59]。实际上，在实验上更常见的是应用单轴应变而不是双轴应变。基于之前的报道[20]，单轴应变可能对单层InSe的热电性能表现出类似的改善。

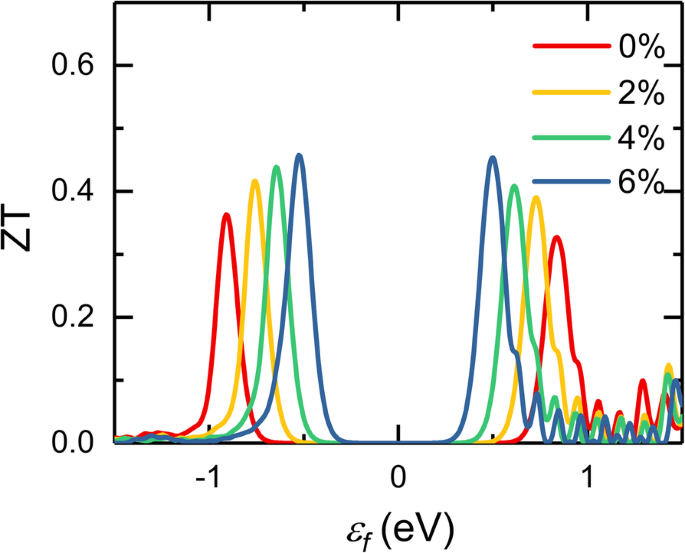
单层InSe在不同应变下作为化学势的函数计算的品质因数

结论

总之，我们通过第一性原理计算系统地研究了双轴拉伸应变对 InSe 单层的电子、热电和声子传输特性的可能影响。带隙随着拉伸应变的增加而减小，导致塞贝克系数减小。拉伸应变还引起更强的非谐散射，晶格热导率的降低可归因于由此产生的声子散射率增加、声子群速度和声子热容降低。晶格热导率的降低大于塞贝克系数的降低，因此随着拉伸应变的增加，性能提高。

数据和材料的可用性

当前研究期间生成和/或分析的数据集可向相应作者索取。

缩写

二维：

二维

CBM：

导带最小值

τ ：

放松时间

C 酸碱度：

声子热容

FET：

场效应晶体管

洛杉矶：

纵向声学声子色散

PF：

功率因数

S ：

塞贝克系数

助教：

横向声学声子色散

VBM：

价带最大值

ZA：

z -轴声学声子色散

ZT：

品质因数

ε :

费米能级

Κ :

电子载流子贡献的热导率

Κ :

晶格贡献的热导率

σ ：

电导率