第一性原理中氮掺杂单层 MoS2 中的光电效应

介绍

寻找新材料并探索它们的奇异特性是现代物理学的一个重要主题。目前，人们对单层二硫化钼 (MoS2) 存在重大兴趣，它与石墨烯类似，可以机械剥离 [1, 2]。与属于间接带隙半导体的块状 MoS2 相比，单层 MoS2 是具有大带隙的直接带隙半导体 [3]。单层 MoS2 具有优异的光学和电学性能 [4]，例如强光吸收 [5-8] 和高载流子迁移率，这有望在晶体管 [9] 和超灵敏光电探测器 [10] 中得到重要应用。此外，最近的 ab initio 研究证明了通过掺杂来调整单层 MoS2 的电子和磁性 [11-19] 的可能性，为具有大潜在容量的自旋电子器件铺平了道路 [20]。

光电流效应 (PGE)，当材料被光照射时会感应出电子电流，可在空间反转对称性破坏的半导体中发生。 PGE 可以由圆偏振光或线偏振光引起，它们分别被称为圆形光电效应 (CPGE) 和线性光伏效应 (LPGE)。最近，已在几种新材料中观察到 PGE [21-26]。例如，发现 GaAs/AlGaAs（一种二维电子气）表现出 LPGE 和 CPGE [27]。在拓扑绝缘体中也发现了 CPGE [28-30]，例如 HgTe 量子阱和 Sb2Te3。值得注意的是，CPGE 已在一些外尔半金属中得到报道 [31-33]。此外，Guo 团队还分析了石墨烯 PN 结和 S 掺杂单层黑磷 [34-36] 中的光响应。有趣的是，LPGE 和 CPGE 都可以表现出零点，其中光电流消失。然而，导致这些零点的机制仍然是一个悬而未决的问题。

已经通过实验 [37-40] 和理论 [11, 41, 42] 分析了单层 MoS2 中的掺杂，特别是对于氮掺杂的单层 MoS2 [38, 43]。在这项工作中，我们对氮掺杂的单层 MoS2 中的 PGE 进行了第一性原理研究。我们发现该材料同时表现出 CPGE 和 LPGE，它们在空间上是各向异性的并且表现出零点。通过对状态联合密度 (JDOS) 和能带结构的综合分析，我们对光电流的行为进行了详细研究。特别是，我们发现 LPGE 和 CPGE 中的零点产生于不同的机制：前者是由前者的禁止跃迁引起的，而后者是由于 Rashba 和 Dresslhaus 自旋轨道耦合的总自旋切缝为零.

模型和方法

首先，几何优化在 CASTEP 包 [44, 45] 中执行。对于掺氮单层 MoS2 的晶胞，采用广义梯度近似 (GGA) 和 Perdew-Burke-Ernzerhof (PBE) 参数化来计算交换和相关势。为了获得高精度的结构，平面波的能量截止值为 500 eV。在倒数空间中，考虑了 6×12×1 k 点。总能量收敛到10 ⁻⁶ e V 并且每个原子上的残余力小于0.01 \(eV/\mathop A\limits ^ \circ \).

接下来，量子传输包Nanodcal [46, 47] 用于JDOS和能带结构的自洽计算，由G补充 G A _P B E 96 为交换关联函数。在这里，使用双 zeta 极化 (DZP) 原子轨道基础来扩展所有物理量。最后，利用格林函数形式和密度泛函理论（NEGF-DFT）计算了器件的光电流。

双探针装置的结构如图 1 所示。在那里，硫原子掺杂有氮原子，它们的比例为 16:1，导致空间反转对称性被破坏。图 1a 显示了一个具有镜像对称性的器件，它在散射区包含 39 个原子。其侧视图[见图1b]，结构优化后获得的松弛构型，说明了氮掺杂单层MoS2的夹心结构。

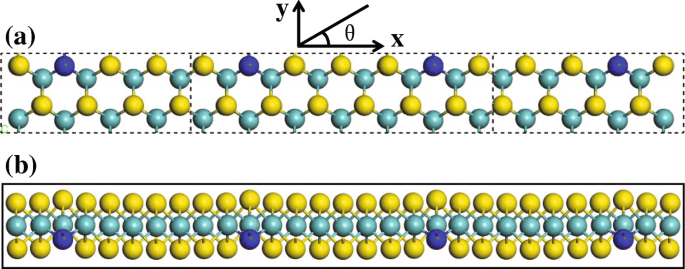
一 用于计算掺氮 MoS2 光电流的双探针器件结构。 b a 的宽松配置的侧视图 . S、Mo和N原子分别用黄色、浅蓝色和深蓝色表示。在没有偏置电压的情况下，散射区被偏振光垂直照射。对于线偏振光，偏振角θ 相对于运输方向测量

掺氮单层MoS2散射区的原子被光垂直照射，其偏振矢量可用下式概括描述

这里，θ 标记线偏振光的偏振角，φ 是描述椭圆偏振光螺旋度的相位角，e α (α =1,2) 表示单位向量。注意φ =±45 ^∘ 对应于右旋/左旋圆偏振光，而 φ =0 对应于线偏振光。由于在所考虑的样本中空间反转对称性被破坏，因此可以生成 PGE。用<I表示从一根引线到中心区域的电流 〉 ^{(p h )} ，我们计算<I 〉 ^{(p h )} 使用 NEGF-DFT 和量子传输包 Nanodcal [46, 47]。对应的归一化光电流由下式给出

在这里，我 ω 是每单位时间通过每单位面积的光子数，即光子通量 [参见参考文献。 [34–36, 48]]。在纳米 , 左电极的光电流 \(I_{L}^{(ph)}\) 可由 [34]

其中 G ^{<(p h )} 和 G ^{>(p h )} 分别是较小的格林函数和较大的格林函数（具有电子-光子相互作用）。 Γ L 表示散射区与左电极的耦合。对于线偏振光，光电流可由下式给出

对于圆偏振光，可以写成

两者，\(G_{1}^{^{> / <\left ({ph} \right)}}\) 和 \(G_{2}^{^{> / <\left ({ph} \right)}}\) 与下面的表达式相同

其中 \(G_{0}^{a}\) 和 \(G_{0}^{r}\) 分别是超前和滞后格林函数（没有光子）。 p α /β 表示电子动量的笛卡尔分量。 e 1/2β 表示单位向量的笛卡尔分量。 N 是光子的数量。 \({C_{0}} ={I_{\omega } }{\left ({e/{m_{0}}} \right)^{2}}\hbar \sqrt {{\mu _{r} }{\varepsilon _{r}}} /2N\omega \varepsilon c\)，其中 c 是速度和ω 是光的频率。 ε 和 ε r 分别是介电常数和相对介电常数。 μ r 表示相对磁化率。 米 0 表示裸电子质量。对于线偏振光，

对于圆偏振光，

我们随后对 PGE 进行分析的一个关键因素是 JDOS，它测量占据价带和未占据导带中电子态之间允许的光学跃迁数量 [49-53]。频率ω的光子激发对应的JDOS 由

其中 E c (k ) 和 E v (k ) 表示动量 k 下电子态的能量 分别在导带和价带。对于具有非退化带的二维系统，JDOS 改写为

结果与讨论

图 2 显示了单层 MoS2 和掺氮单层 MoS2 的能带结构。在之前的文献中，单层 MoS2 是一种带隙为 1.90 eV 的直接带隙半导体 [3, 4]。为了比较[见图2a]和掺杂之前的能带结构，我们在布里渊区选择相同的路径。对于氮掺杂的单层 MoS2，观察到一个穿过费米能级的杂质诱导带，它靠近价带的顶部 [见图 2b]。因此，氮掺杂的单层 MoS2 是 p 型半导体。重要的是，由于空间反转对称性被破坏，即使没有外部电压，原始单层 MoS2 的能带在掺杂的情况下也会进一步分裂。众所周知，这种能带分裂将允许在圆偏振光照射下进行自旋轨道耦合，为CPGE提供了重要的机制。

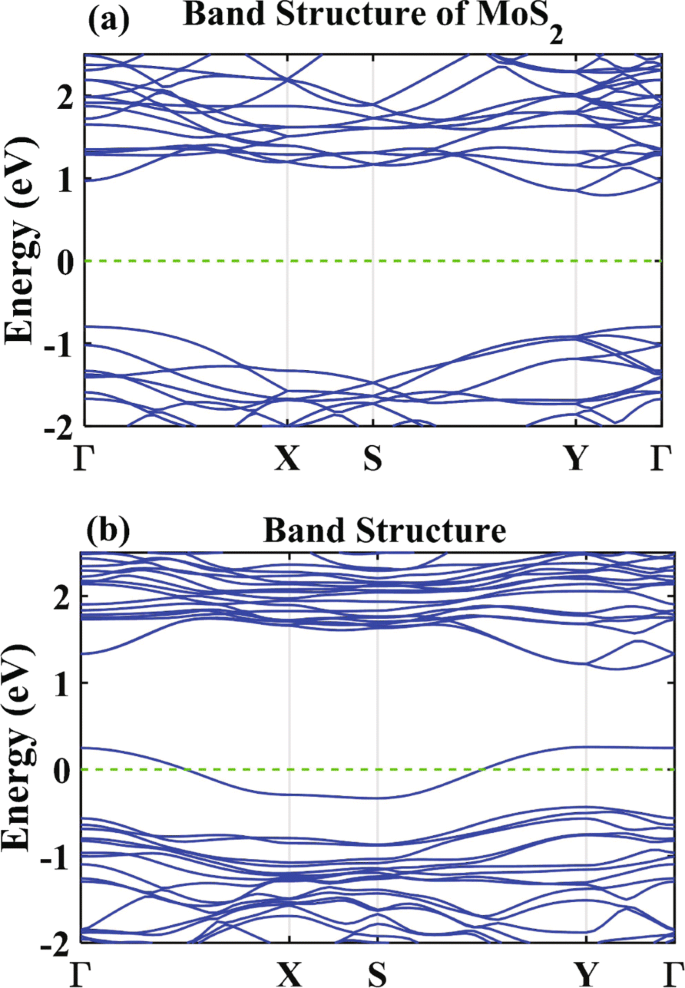
a 的能带结构 单层 MoS2 和 b 氮掺杂单层二硫化钼

我们现在研究通过 NEGF-DFT 计算获得的在垂直光照射下氮掺杂单层 MoS2 的光响应。图 3 显示了 LPGE 和 CPGE 的光响应函数。对于液化石油气，θ =π /4 和 φ =0 ^∘ .对于 CPGE，θ =0 ^∘ 和φ =π /4。光子能量范围为 0 到 2.3 eV（间隔为 0.1 eV）。在图 3 中，CPGE 在氮掺杂单层 MoS2 中的光响应比 LPGE 强两个数量级。 LPGE 的光响应在整个范围内保持很小，这是器件结构对称性的直接结果。相比之下，CPGE 在 0.7 eV 之后出现，接近高对称点 Y 处杂质带与导带之间的能隙 [见图 2b]。这意味着电子跃迁是直接的。此外，当光子能量高于 1.7 eV 时，CPGE 变得很重要。当光子能量进一步增加时，光响应的大小呈非线性变化，方向由正转负。

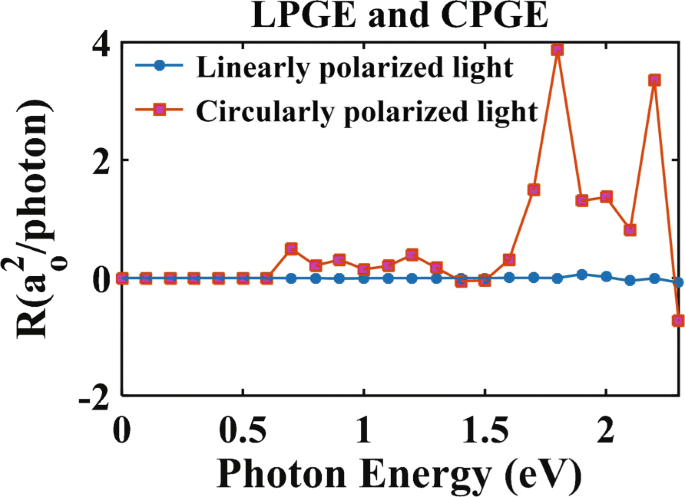
光响应函数分别随线偏振光和圆偏振光能量的变化。对于液化石油气，θ =π /4 和 φ =0 ^∘ .对于 CPGE，θ =0 ^∘ 和φ =π /4。光子能量范围从 0 到 2.3 eV，间隔为 0.1 eV

为了直观了解上述现象，我们注意到光电流与光吸收系数 α 密切相关 由

在这里，n 是折射率，c 0 表示真空中的光速，m e 标记电子的质量。此外，s 表示电磁波矢量势的单位矢量。矩阵元素M 简历 对应于动量 p 并具有形式<c ,k |p |v ,k 〉, 用 |v (c ),k 〉 为拟动量 k 处的电子态 在价（导）带。注意光电流的发生需要α>0.方程 (12) 意味着光电流主要取决于两个量：矩阵元素 M 简历 和 JDOS。

图 4 显示了示例的 JDOS。对于低于 0.5 eV 的光子能量，JDOS 几乎消失，表明电子几乎不能被激发。然而，当光子能量超过 0.5 eV 时，JDOS 中会出现一系列峰值。在图 4 中，两个峰值出现在光子能量 0.69 eV 和 0.76eV 处（见绿色虚线）。这对应于在高对称点 Y 和 Γ 处将电子从价带激发到杂质带的最小能量 [见图2b]，分别。此外，当光子能量取值为 0.94 eV、1.03 eV 和 1.925 eV 时，也会观察到峰值。它们对应于电子在高对称点 Y 处从杂质带到导带的光激发，Γ , 和 S 分别。此外，1.65 eV 和 1.89 eV 处的峰值（黑色虚线）对应于高对称点 Y 和 Γ 从价带到导带的电子跃迁 分别。在 1.89 eV 之后，JDOS 像指数函数一样急剧增加，其趋势与光吸收率实验一致[40]。此外，我们的研究结果表明，氮掺杂的单层MoS2在可见光范围内具有很强的光吸收，这也与实验结果一致。

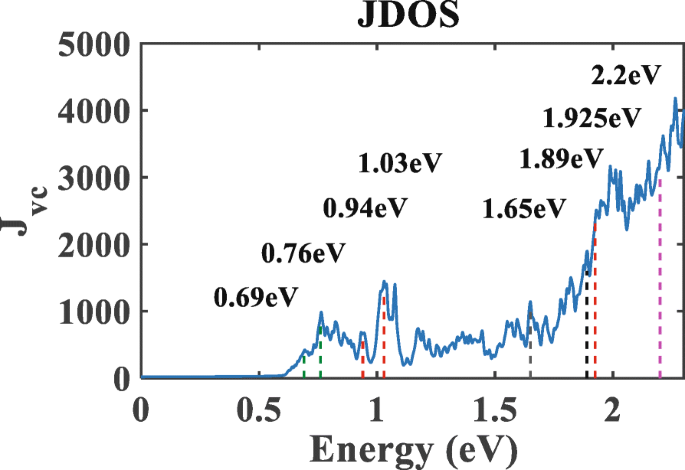
氮掺杂单层 MoS2 的联合态密度。虚线表示能量临界点

对比图 4 和图 3 表明 JDOS 和光响应之间的密切联系。在那里，JDOS 和光响应在低于 0.5 eV 的光子能量下几乎为零，在 0.6 到 1.7 eV 的范围内变为非零 - 但仍然很小，然后在 1.7 到 2.3 eV 的范围内显着上升并剧烈波动。特别是当光子能量为 1.7 eV 时，CPGE 的光响应表现出明显的峰值。结合图 2b，我们知道电子可能有两个使用杂质带的跃迁，因为从价带到传导的 1.7 eV 光子能量激发的电子是有限的。然而，光响应具有最大振幅，因为电子可以从价带转移到杂质带，然后从杂质带转移到导带。

为了进一步了解光电流的行为，我们接下来将 LPGE 的光响应绘制为偏振角 θ 的函数 [见图5a]。人们发现光响应的幅度表现为∼ sin(2θ ）。这与具有 C 的材料的 LPGE 的现象学理论一致 s 法向入射下的对称性，其中 \({R_{x}} {\propto } E_{0}^{2}{\chi _{xxy}}\sin \left ({2\theta } \right)\) [ 21, 26, 54–56] 与 E 0 光的电场强度和χ xxx 作为张量。有趣的是，虽然光响应函数表现为 sin(2θ ) 当光子能量为 2.0 eV 时，变为 − sin(2θ ) 当光子能量为 2.1 eV 时。因此，在 2.0 eV 和 2.1 eV 之间必然存在光电流消失的点，即 LPGE 的零点。为了定位零点，我们使用基于二分法的方法并绘制光响应相对于线偏振光能量的变化。对于θ，如图5b所示 =π /4 度，零点出现在 2.0012 eV 的光子能量上。正如前面根据方程指出的那样。 (12)，光电流取决于 JDOS 和动量矩阵元素。由于在我们的计算中总是发现JDOS是有限的，因此零点的出现只能归因于电子跃迁的不存在，即在这种情况下零点的存在是由于禁止跃迁。

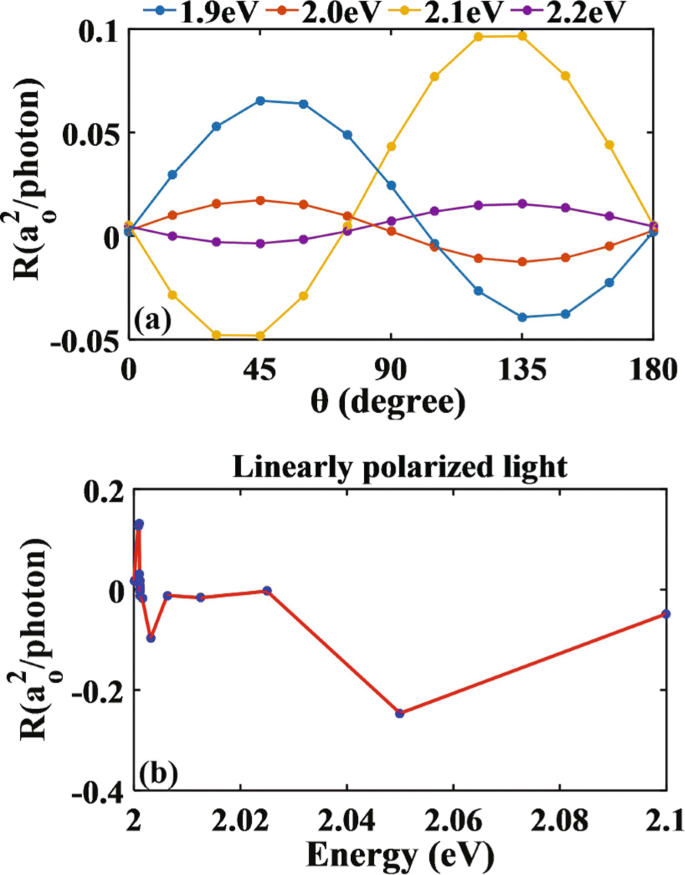
线偏振光垂直照射氮掺杂单层二硫化钼的光响应函数行为。光响应函数随a的变化 偏振角和 b θ 线偏振光的能量 =π /4

为了比较，CPGE 的光响应作为相位角的函数 ϕ 总结在图 6 中。人们发现 R x ∼ sin(2ϕ )，再次与现象学预测一致，该预测给出 \({R_{x}} {\propto } E_{0}^{2}{\gamma _{xz}}\sin \left ({2\phi } \右)\) 与 γ xz 作为张量。与 LPGE 类似，CPGE 也表现出零点，它发生在图 6b 中的 2.2560 eV。在那里，转移矩阵总是有限的，因此，这个零点不能像 LPGE 那样用禁止转移来解释。相反，我们援引了这样一个事实，即 CPGE 与 Rashba SOC 和 Dresslhaus SOC 都密切相关，它们分别影响不同强度的价带和导带的分裂。在两个能带中分裂相同的特定情况下，导带中的激发电子将在±k处具有相反的动量 x .结果，导带中的净电子电流为零，从而解释了CPGE零点的存在。

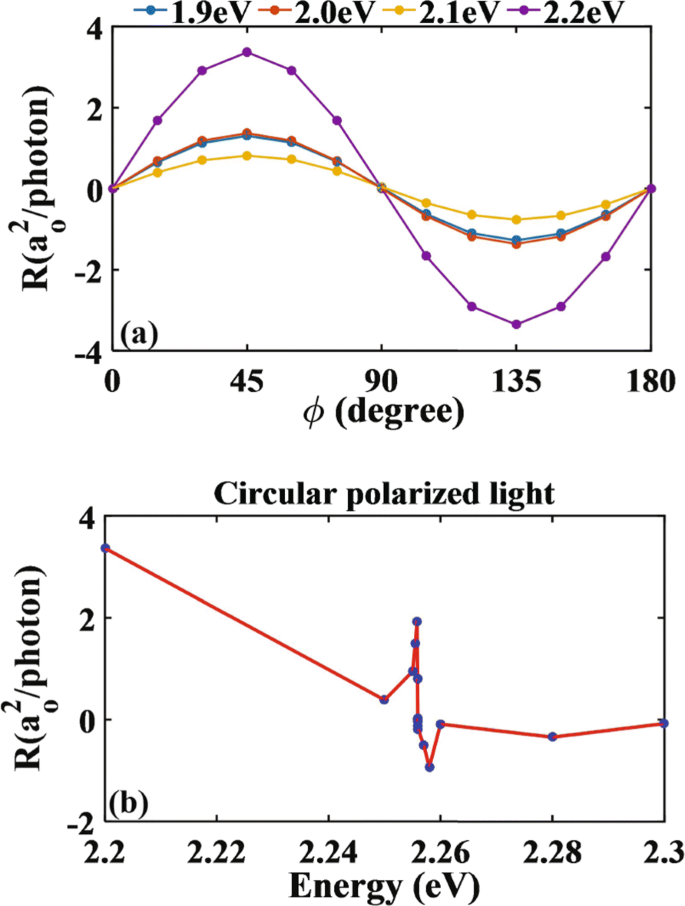
椭圆偏振光垂直照射掺氮单层二硫化钼。 一 , b φ光响应函数随相位角和圆偏振光能量的变化 =45 ^o , 分别

有趣的是，CPGE 在氮掺杂单层 MoS2 中的光响应比 LPGE 强两个数量级，如图 1 和图 3 所示。 3、5和6。这可以理解如下。对于 LPGE，光电流是由载流子的不对称散射引起的。相比之下，CPGE 的产生是因为当材料受到照射时，导带中的电子在 Rashba SOC 和 Dresslhaus SOC 下表现出不平衡的占据：在照射之前，由于氮掺杂单层 MoS2 的空间逆对称性破缺，原始样品的能带用 Dresslhaus SOC 提升。然后，当材料受到圆偏振光的照射时，光子的角动量通过 Rashba SOC 转换为电子的自旋角动量。作为总体结果，满足光学选择规则 \(\Delta {m_{s}} =0,\begin {array}{*{20}{c}}\end {array} \pm 1\) 的电子可以被激发到导带。这与 LPGE 不同，LPGE 在线偏振光下电子的自旋角动量保持不变，即 Δ 米 s =0 代表液化石油气。因此，由于 CPGE 的 Rashba SOC 和 \(\Delta {m_{s}} \begin {array}{*{20}{c}}\end {array} \pm 1\)，电子的跃迁概率将CPGE 显着增加，有助于更强的光响应。

最后，从我们的计算中可以看出，在我们的系统中，光子能量在没有外部偏置的情况下转化为电能，并且对于掺氮单层 MoS2 的可见光吸收很强，尤其是从 1.6 到 2.3 eV [见图 3]，即，从红光到绿光。因此，它是二维光伏器件 [57]、rgb 1.00,0.00,0.00lasers [58] 和单光子发射器 [59] 的合适材料。此外，对于给定的光子能量 R，光响应随偏振和相位角有规律地变化 ∼ sin(2θ ）。因此，控制极化和相位角以控制光电流是有用的。然而，LPGE 是轻微的，这促使我们的实验者使用圆偏振光以获得大的光电流。此外，JDOS能带结构的分析给出了光电流的合理解释，为光电实验结果提供了理论依据。

结论

总之，我们已经提出了基于 NEGF-DFT 在垂直照射下氮掺杂单层 MoS2 中 PGE 的第一性原理研究。我们对光响应的行为提供了令人满意的解释，这是通过结合对能带结构和联合态密度的分析来实现的。我们发现LPGE和CPGE的光电流都存在零点，但潜在的机制不同。对于 LPGE，零点出现在 2.0012 eV 的光子能量处，其中与从价带到导带的电子激发相关的跃迁矩阵元素消失，即禁止跃迁。另一方面，对于 CPGE，光子能量为 2.2560 eV 时光电流为零，虽然始终允许相关转变，但 Rashba SOC 和 Dresslhaus SOC 的存在导致净零电流。此外，CPGE 在氮掺杂单层 MoS2 中的光响应比 LPGE 强两个数量级。通常，我们可以通过改变光子能量、偏振光类型和偏振角来有效控制二维光伏器件中的光电流。目前的理论工作可能为纳米材料光电化学效应的探索提供启示，并为涉及单层MoS2的光电和光伏应用开辟新的途径。

数据和材料的可用性

本研究中生成或分析的所有数据均包含在本文中。

缩写

CPGE：

圆形光电效应

液化石油气：

线性光伏效应

JDOS：

联合态密度

GGA：

广义梯度逼近

PBE：

Perdew-Burke-Ernzerhof

DZP：

双zeta极化

DFT：

密度泛函理论

NEGF：

非平衡格林函数法