







Simulink 是一个用于动态和嵌入式系统的仿真和基于模型的设计环境,与 MATLAB 集成。 Simulink 同样由 MathWorks 开发,是一种数据流图形化编程语言工具,用于对多域动态系统进行建模、仿真和分析。它基本上是一个图形框图工具,带有可自定义的块库集。 它允许您将 MATLAB 算法整合到模型中,并将仿真结果导出到 MATLAB 中进行进一步分析。 Simulink 支持 - 系统级设计 模拟 自动代码生成 嵌入式系统的测试和验证 MathWorks 提供的其他几个附加产品以及可与 Simulink 一起使用的第三方硬件和软件产品。 以下列表简要说明了其中一些
GNU Octave 是一种类似于 MATLAB 的高级编程语言,它主要与 MATLAB 兼容。它也用于数值计算。 Octave 与 MATLAB 有以下共同特点 - 矩阵是基本的数据类型 它内置了对复数的支持 它具有内置的数学函数和库 支持用户自定义函数 GNU Octave 也是可自由再分发的软件。您可以根据自由软件基金会发布的 GNU 通用公共许可证 (GPL) 条款重新分发和/或修改它。 MATLAB 与 Octave 大多数 MATLAB 程序在 Octave 中运行,但某些 Octave 程序可能无法在 MATLAB 中运行,因为 Octave 允许一些 MATLAB 不

MATLAB 提供了用于处理变换的命令,例如拉普拉斯变换和傅里叶变换。转换在科学和工程中被用作简化分析和从另一个角度查看数据的工具。 例如,傅里叶变换允许我们将表示为时间函数的信号转换为频率函数。拉普拉斯变换允许我们将微分方程转换为代数方程。 MATLAB 提供了 laplace , 傅立叶 和 fft 用于处理拉普拉斯、傅里叶和快速傅里叶变换的命令。 拉普拉斯变换 时间函数 f(t) 的拉普拉斯变换由以下积分给出 - 拉普拉斯变换也表示为 f(t) 到 F(s) 的变换。可以看到这个变换或积分过程将符号变量 t 的函数 f(t) 转换成另一个函数 F(s) 和另一个变量 s。 拉
MATLAB 将多项式表示为包含按降幂排序的系数的行向量。例如,方程 P(x) =x4 + 7x3 - 5x + 9 可以表示为 - p =[1 7 0 -5 9]; 计算多项式 多边形 函数用于计算指定值的多项式。例如,要评估我们之前的多项式 p ,在 x =4 处,键入 - 现场演示 p = [1 7 0 -5 9]; polyval(p,4) MATLAB 执行上述语句并返回以下结果 - ans = 693 MATLAB 还提供了 polyvalm 用于评估矩阵多项式的函数。矩阵多项式是多项式 以矩阵为变量。 例如,让我们创建一个方阵 X 并计算多项式 p,在 X -

集成处理两种本质上不同类型的问题。 在第一种类型中,给出了函数的导数,我们想要找到该函数。因此,我们基本上扭转了分化的过程。这个逆过程称为反微分,或求原函数,或求不定积分 . 第二种类型的问题涉及将大量非常小的数量相加,然后在数量的大小接近零时取一个极限,而项的数量趋于无穷大。这个过程导致了定积分的定义 . 定积分用于求面积、体积、重心、惯性矩、力所做的功,以及许多其他应用。 使用 MATLAB 求不定积分 根据定义,如果函数 f(x) 的导数是 f(x),那么我们说 f(x) 关于 x 的不定积分是 f(x)。例如,由于 x2 的导数(关于 x) 是 2x,我们可以说 2
MATLAB 提供了 diff 用于计算符号导数的命令。在最简单的形式中,您将要区分的函数作为参数传递给 diff 命令。 例如,让我们计算函数 f(t) =3t2 的导数 + 2t-2 示例 创建一个脚本文件并在其中输入以下代码 - syms t f = 3*t^2 + 2*t^(-2); diff(f) 当上面的代码编译并执行时,它会产生以下结果 - ans = 6*t - 4/t^3 以下是上述计算的八度等价 - pkg load symbolic symbols t = sym(t); f = 3*t^2 + 2*t^(-2); differentiate(f,t
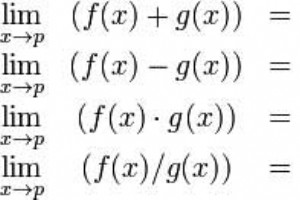
MATLAB 提供了多种解决微积分和积分问题、求解任意阶微分方程和计算极限的方法。最重要的是,您可以通过求解原始函数及其导数,轻松绘制复杂函数的图形,并检查图形上的最大值、最小值和其他固定点。 本章将处理微积分问题。在本章中,我们将讨论微积分前的概念,即计算函数的极限和验证极限的性质。 下一章微分 ,我们将计算表达式的导数并在图上找到局部最大值和最小值。我们还将讨论求解微分方程。 最后,在集成 本章,我们将讨论积分。 计算限制 MATLAB 提供了 limit 用于计算限制的功能。在其最基本的形式中,limit 函数将表达式作为参数,并在自变量变为零时找到表达式的极限。 例如,让我们

到目前为止,我们已经看到所有示例都在 MATLAB 以及它的 GNU(也称为 Octave)中工作。但是对于基本代数方程的求解,MATLAB 和 Octave 的区别不大,所以我们将尝试将 MATLAB 和 Octave 分开来介绍。 我们还将讨论代数表达式的因式分解和化简。 在 MATLAB 中求解基本代数方程 解决 函数用于求解代数方程。在最简单的形式中,solve 函数将用引号括起来的方程作为参数。 例如,让我们在方程 x-5 =0 中求解 x solve(x-5=0) MATLAB 将执行上述语句并返回以下结果 - ans = 5 您也可以将求解函数称为 -
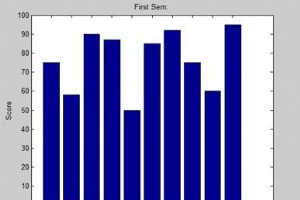
本章将继续探索 MATLAB 的绘图和图形功能。我们将讨论 - 绘制条形图 绘制轮廓 三维绘图 绘制条形图 栏 命令绘制一个二维条形图。让我们举个例子来说明这个想法。 示例 让我们有一个 10 名学生的假想教室。我们知道这些学生获得的分数百分比分别为 75、58、90、87、50、85、92、75、60 和 95。我们将为此数据绘制条形图。 创建一个脚本文件并输入以下代码 - x = [1:10]; y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95]; bar(x,y), xlabel(Student),ylabel(Score), title
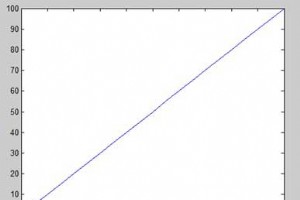
要绘制函数图,您需要执行以下步骤 - 定义 x ,通过指定值的范围 对于变量 x , 为其绘制函数 定义函数,y =f(x) 调用情节 命令,如 plot(x, y) 以下示例将演示该概念。让我们绘制简单函数 y =x x 的取值范围为 0 到 100,增量为 5。 创建一个脚本文件并输入以下代码 - x = [0:5:100]; y = x; plot(x, y) 运行文件时,MATLAB 会显示以下图 - 让我们再举一个例子来绘制函数 y =x2 .在本例中,我们将使用相同的函数绘制两个图形,但在第二次中,我们将减小增量的值。请注意,随着我们减少增量

MATLAB 中的数据导出(或输出)是指写入文件。 MATLAB 允许您在另一个读取 ASCII 文件的应用程序中使用您的数据。为此,MATLAB 提供了多种数据导出选项。 您可以创建以下类型的文件 - 来自数组的矩形、分隔的 ASCII 数据文件。 击键的日记(或日志)文件和结果文本输出。 使用 fprintf 等低级函数的专用 ASCII 文件。 MEX 文件,用于访问写入特定文本文件格式的 C/C++ 或 Fortran 例程。 除此之外,您还可以将数据导出到电子表格。 有两种方法可以将数值数组导出为分隔的 ASCII 数据文件 - 使用保存 函数

在 MATLAB 中导入数据意味着从外部文件加载数据。 导入数据 功能允许加载不同格式的各种数据文件。它有以下五种形式 - Sr.No. 功能与说明 1 A =导入数据(文件名) 将数据从 filename 表示的文件加载到数组 A . 2 A =importdata(-pastespecial) 从系统剪贴板而不是从文件中加载数据。 3 A =importdata(___, delimiterIn) 解释 delimiterIn 作为 ASCII 文件、文件名或剪贴板数据中的列分隔符。您可以使用 delimiterIn 使用上述语法中的任何输入参数。 4

函数是一组一起执行任务的语句。在 MATLAB 中,函数在单独的文件中定义。文件名和函数名要一致。 函数在它们自己的工作区(也称为本地工作区)内对变量进行操作 ,与您在 MATLAB 命令提示符下访问的工作区(称为 基本工作区)分开 . 函数可以接受多个输入参数,也可以返回多个输出参数。 函数语句的语法是 - function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN) 示例 以下函数名为 mymax 应该写在一个名为 mymax.m 的文件中 .它接受五个数字作为参数,并返回最大的数字。 创建一个名为 mymax.

在 MATLAB 中创建字符串非常简单。事实上,我们已经用过很多次了。例如,您在命令提示符下键入以下内容 - 现场演示 my_string = Tutorials Point MATLAB 将执行上述语句并返回以下结果 - my_string = Tutorials Point MATLAB 将所有变量视为数组,将字符串视为字符数组。让我们使用 whos 检查上面创建的变量的命令 - whos MATLAB 将执行上述语句并返回以下结果 - Name Size Bytes Class Attributes my_string

MATLAB 支持各种数值类,包括有符号和无符号整数以及单精度和双精度浮点数。默认情况下,MATLAB 将所有数值存储为双精度浮点数。 您可以选择将任意数字或数字数组存储为整数或单精度数字。 所有数值类型都支持基本的数组运算和数学运算。 转换为各种数值数据类型 MATLAB 提供以下函数来转换为各种数值数据类型 - 函数 目的 双倍 转换为双精度数 单人 转换为单精度数 int8 转换为 8 位有符号整数 int16 转换为 16 位有符号整数 int32 转换为 32 位有符号整数 int64 转换为 64 位有符号整数 uint8 转换为 8 位无符号整数 uint1

冒号(:) 是 MATLAB 中最有用的运算符之一。它用于创建向量、下标数组和指定迭代 . 如果你想创建一个行向量,包含从 1 到 10 的整数,你可以写 - 现场演示 1:10 MATLAB 执行该语句并返回一个包含从 1 到 10 的整数的行向量 - ans = 1

MATLAB中所有数据类型的所有变量都是多维数组。向量是一维数组,矩阵是二维数组。 我们已经讨论过向量和矩阵。在本章中,我们将讨论多维数组。不过,在此之前,让我们讨论一些特殊类型的数组。 MATLAB 中的特殊数组 在本节中,我们将讨论一些创建一些特殊数组的函数。对于所有这些函数,一个参数创建一个方形数组,双参数创建一个矩形数组。 zeros() 函数创建一个全为零的数组 - 例如 - 现场演示 zeros(5) MATLAB 将执行上述语句并返回以下结果 - ans = 0 0 0 0 0 0 0 0

矩阵是数字的二维数组。 在 MATLAB 中,您可以通过在每行中输入以逗号或空格分隔的数字形式的元素并使用分号标记每行的结尾来创建矩阵。 例如,让我们创建一个 4×5 矩阵 a - 现场演示 a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] MATLAB 将执行上述语句并返回以下结果 - a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6

向量是数字的一维数组。 MATLAB 允许创建两种类型的向量 - 行向量 列向量 行向量 行向量 通过将一组元素括在方括号中,使用空格或逗号分隔元素来创建。 现场演示 r = [7 8 9 10 11] MATLAB 将执行上述语句并返回以下结果 - r = 7 8 9 10 11 列向量 列向量 通过将一组元素括在方括号中,使用分号分隔元素来创建。 现场演示 c = [7; 8; 9; 10; 11] MATLAB 将执行上述语句并返回以下结果 - c = 7 8 9
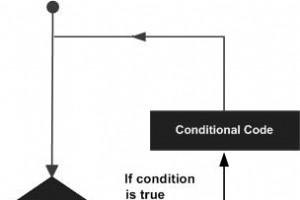
可能存在需要多次执行一段代码的情况。通常,语句是按顺序执行的。函数中的第一条语句首先执行,然后是第二条,依此类推。 编程语言提供了各种控制结构,允许更复杂的执行路径。 循环语句允许我们多次执行一个语句或一组语句,以下是大多数编程语言中循环语句的一般形式 - MATLAB 提供以下类型的循环来处理循环要求。单击以下链接以查看其详细信息 - Sr.No. 循环类型和描述 1 while 循环 在给定条件为真时重复一个语句或一组语句。它在执行循环体之前测试条件。 2 for 循环 多次执行一系列语句并缩写管理循环变量的代码。 3 嵌套循环 您可以在任何另一个循环中使用一个或多
MATLAB