研究纳米粒子聚集/附聚对聚合物纳米复合材料杨氏模量影响的两步法

背景

近年来，许多研究人员专注于聚合物纳米复合材料，以确定加工-结构-性能关系中的有效参数，并优化通过机械、热、物理和阻隔性能衡量的整体性能 [1,2,3,4 ]。聚合物纳米复合材料中纳米颗粒含量低，可产生大界面面积、高模量、低重量和廉价的产品，这些产品在复合材料行业极具吸引力。因此，纳米粒子的应用是提高聚合物基质性能的一种简单、有效且经济的方法。许多材料和加工参数对包含硅酸盐层（纳米粘土）、碳纳米管 (CNT) 和无机填料（如二氧化硅 (SiO2) 和碳酸钙 (CaCO3)）的聚合物纳米复合材料的性能的影响已得到研究 [5,6 ,7,8]。

纳米粒子在聚合物基体中的尺寸和分散/分布质量改变了聚合物纳米复合材料的一般性质。由于纳米粒子之间的吸引力，例如范德华力和化学键 [9]，或者随着填料尺寸的减小，表面分离的强烈减少 [10]，纳米粒子倾向于聚集和附聚。因此，很难将纳米颗粒以纳米级分散在聚合物基质中。聚集和团聚都是纳米粒子的集合，其中聚集包括强而密的粒子群，但团聚包含松散结合的粒子，这些粒子可以被机械力破坏。团聚/聚集在高填料含量下很明显，这会破坏填料的纳米级并在纳米复合材料中产生许多缺陷和应力集中 [11,12,13]。附聚/聚集还减少了聚合物基体和纳米粒子之间的界面面积，这减少了聚合物链在纳米粒子中的机械参与并消除了硬化效应。我们最近的发现 [14, 15] 以及 Ji 等人的研究。 [16] 关于力学性能的研究表明，任何聚集/团聚都会严重破坏纳米粒子在聚合物纳米复合材料中的硬化效果。

除了纳米复合材料的实验表征之外，量化力学行为对组成相性质和纳米粒子几何形态的依赖性的理论研究在最近的研究中引入了有吸引力的挑战。理论研究可能有助于阐明实验结果并促进极具前景的纳米复合材料的最佳合成。纳米复合材料中的纳米颗粒将无序引入相邻基体，导致在填料周围形成界面区，显示出与块体基体和纳米颗粒不同的特性 [17,18,19]。界面性质的理论研究显示出有吸引力的结果，证明纳米粒子在聚合物纳米复合材料中的应用是合理的[20,21,22]。

聚集/团聚对纳米复合材料机械性能的影响在以前的工作中进行了研究 [11, 14, 23, 24]。这些研究通常考虑大颗粒的聚集/附聚。最近，多尺度建模方法已被用于研究纳米复合材料的特性 [25,26,27]。在目前的论文中，建议采用两步法来检查纳米颗粒聚集/附聚在聚合物纳米复合材料杨氏模量中的作用，假设纳米复合材料中的聚集/附聚相部分和纳米颗粒在聚集体/附聚物中的部分。在这方面，应用 Paul 和 Maxwell 的两个微机械模型来表达纳米复合材料的杨氏模量。提供了大量实验数据来评估预测。此外，还研究了聚集/团聚参数对纳米复合材料杨氏模量的影响。

方法

当一小部分纳米尺寸的颗粒聚集/附聚时，纳米复合材料中会出现纳米颗粒的不均匀分布。因此，一些纳米粒子可以假设在基质中的球形区域中作为聚集/附聚相，而其他纳米粒子则均匀分散在聚合物基质中，如图 1 所示。因此，纳米填料显示出具有不同增强作用的两个部分，它们可以是将计算中的两个不同阶段视为聚集/附聚和有效基质阶段，分别显示球体内部和外部区域（图 1）。

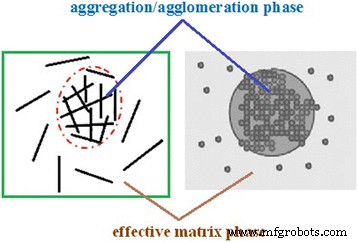
含有层状和球形纳米粒子的聚合物纳米复合材料中聚集/团聚和有效基体相的示意图

聚合物纳米复合材料中纳米颗粒的聚集/团聚水平建议采用以下两个参数：

其中“V agg”和“V ”分别表示聚集/团聚相和纳米复合材料的总体积。此外，“V f ^agg ”和“V f”分别显示聚集/附聚阶段和整个纳米复合材料中纳米粒子的体积。聚集/附聚相中纳米颗粒的体积分数表示为：

其中“φ f ”是纳米复合材料中纳米填料的体积分数。此外，掺入有效基质相（脱离聚集/附聚相）的分散良好的纳米颗粒的体积分数计算如下：

在本研究中，基于微机械模型的两步法用于确定聚集/附聚参数 (z 和 y ) 在聚合物纳米复合材料中的杨氏模量。首先，聚集/附聚和有效基质相的模量由保罗模型计算。其次，将聚集/团聚相假定为有效基体中的球形夹杂物，并通过麦克斯韦模型计算了纳米复合材料的杨氏模量，用于含有分散颗粒的复合材料。

Paul [28] 提出了一个模型，该模型假设复合材料的两个组件的宏观应力为：

其中“E m”和“E f”分别是聚合物基体和填料相的杨氏模量。第一步，聚集/附聚模量 (E agg) 和有效矩阵 (E mat) 相位由 Paul 模型通过替换“ϕ f ” 与“\( {\phi}_f^{agg} \)”和“\( {\phi}_f^{mat} \)”为：

此外，含有分散填料的复合材料的 Maxwell 模型 [29] 由下式给出：

在第二步中，通过替换“φ f ” 与“z ”（见等式 1），“E f” 与聚集/附聚阶段的模量 (E agg) 和“E m” 与有效矩阵的模数 (E 垫）为：

它将纳米复合材料的杨氏模量与聚集体/附聚物的模量和有效基体以及“z”参数相关联。当“E agg”和“E 垫子”来自方程式。将7和8输入到后面的方程中，纳米复合材料的模量用填料浓度、填料模量、基体模量和“z”表示 ” 和 “y “ 参数。模量对这些参数的依赖性是合理的，因为聚合物和纳米颗粒的性质以及填料聚集/附聚的程度控制着纳米复合材料的模量。在本方法中，y> z 是有意义的，因为 \( {VV}_f^{\mathrm{agg}}>{V}_f{V}_{\mathrm{agg}} \).

结果与讨论

所提出的方法用于评估先前研究中的几个样品中纳米颗粒的聚集/团聚，包括 PVC/CaCO3 [30]、PCL/纳米粘土 [31]、ABS/纳米粘土 [32]、PLA/纳米粘土 [33]、PET/MWCNT [ 34]，和聚酰亚胺/多壁碳纳米管 [35]。图 2 显示了杨氏模量的实验结果以及两步法的预测。计算正确地遵循了不同纳米填料浓度下的实验数据，说明了所建议方法的正确性。然而，当纳米粒子的聚集/团聚由适当水平的“z ” 和 “y “ 参数。 “z”的最高预测 ” 和 “y ” 参数计算为z =0.2 和 y 对于 PVC/CaCO3 纳米复合材料，=0.95。此外， (z , y ) 分别为 PCL/纳米粘土、PLA/纳米粘土和 PET/MWCNT 样品获得 (0.3, 0.75)、(0.1, 0.99) 和 (0.35, 0.7) 值。此外， (z , y ) 分别为 PET/MWCNT 和聚酰亚胺/MWCNT 纳米复合材料计算了 (0.2, 0.93) 和 (0.15, 0.9) 水平。这些级别的“z ” 和 “y ” 参数证明了在提到的纳米复合材料中聚集/附聚的纳米颗粒的形成。这些样品中模量的小幅提高证实了聚合物基质中纳米颗粒的分散性弱和高水平的积累。例如，向 PVC 添加 7.5 wt% CaCO3 只会将纯 PVC (1.13 GPa) 的模量增加到 1.3 GPa。此外，在 PCL 中加入 10 wt% 的纳米粘土只会将纯 PCL 的模量从 0.22 GPa 提高到 0.37 GPa。然而，与聚合物基质相比，纳米颗粒显示出高模量。据报道，CaCO3、纳米粘土和 MWCNT 的杨氏模量分别为 26、180 和 1000 GPa [36]，而本聚合物基质的杨氏模量几乎不达到 2.5 GPa。因此，聚集/附聚的纳米颗粒显着降低了纳米复合材料的模量，本方法为聚合物纳米复合材料中纳米颗粒的聚集/附聚提供了可接受的数据。

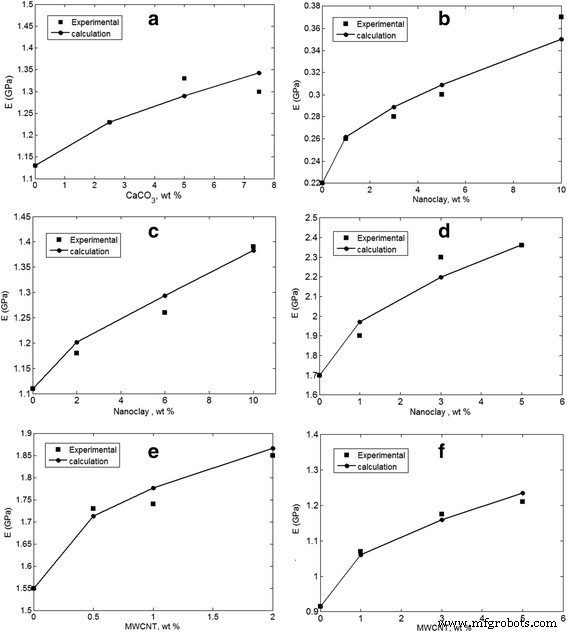
假设 a 的纳米颗粒聚集/团聚，实验结果与理论结果之间的差异 PVC/CaCO3 [30], b PCL/纳米粘土 [31]，c ABS/纳米粘土 [32]，d PLA/纳米粘土 [33]，e PET/MWCNT [34] 和 f 聚酰亚胺/多壁碳纳米管 [35] 样品

通过当前方法预测的最高和最小模量计算并在图 3 中说明，平均 E m =2 GPa 和 E f =200 GPa。最大模数由“z”的最小值获得 ” 和 “y “ 参数;例如，z =0.00001 和 y =0.00001（它们不能为 0）。另一方面，“y ” 0.99 的水平导致所有纳米粒子的聚集/团聚，这显着降低了模量。此外，最高级别的“z ”（最大聚集程度）导致最小模量。 “z ”因为纳米复合材料中团聚填料的体积分数小于所有纳米粒子的体积分数（φ f ）。所以，z =φ f 可以暗示最轻微的模量水平。模量的上限和下限之间的显着差异表明纳米颗粒的聚集/团聚在纳米复合材料的刚度中的重要作用。纳米复合材料中纳米颗粒的聚集/团聚大大降低了不同填料浓度下的杨氏模量，而没有聚集/团聚的纳米颗粒的精细分散产生了良好的模量。此外，随着“φ f ”。因此，调整材料和工艺参数以防止纳米颗粒的聚集/团聚，从而促进聚合物纳米复合材料中的应力集中和缺陷或脱粘是很重要的[37, 38]。

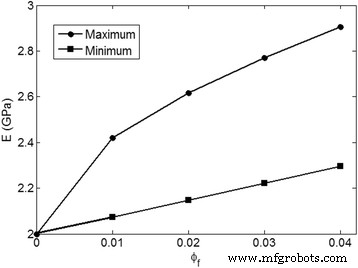
本方法预测的最大和最小模量水平在平均 E m =2 GPa 和 E f =200 GPa

图 4 说明了“z ” 和 “y ” E 处的模数参数 m =3 GPa, E f =150 GPa，并且 ϕ f =0.02。在“z”的最小水平上获得最高模量 ” 和 “y ”参数，证实了纳米粒子的良好分散/分布对纳米复合材料的模量的积极作用。然而，模量随着“y ”参数增加。根据方程。 2、“y ”显示了聚集/聚集相中纳米颗粒的浓度。在高“y”下观察到低模量 ”水平，这表明聚集/聚集相中的大部分纳米颗粒削弱了纳米复合材料。因此，附聚/聚集的纳米粒子对纳米复合材料的模量产生负面影响。因此，应该做出很多努力来促进纳米颗粒在聚合物基质中的分散/分布，这取决于聚合物和纳米颗粒之间的界面相互作用/粘附以及加工参数。先前的研究报告了该领域的有价值的结果，并提出了各种技术来改善这种分散[39,40,41]。

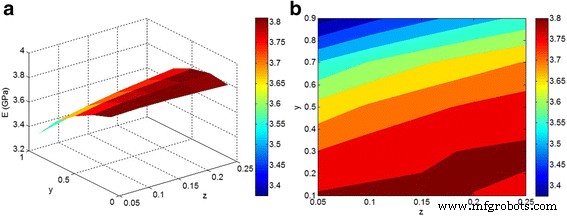
一 , b 通过方程计算模量。 10-11 作为“z”的函数 ” 和 “y ” 在 E m =3 GPa, E f =150 GPa，并且 ϕ f =0.02

图 5 展示了预测模量对“E m”和“E f” 平均参数ϕ f =0.02, z =0.3，并且 y =0.5 使用当前技术。据观察，模量取决于“E m”和“E f” 因素在低 E f <150 GPa。然而，纳米颗粒的更高模量不会改变纳米复合材料的模量。因此，纳米复合材料的模量仅取决于“E m” 当“E f”高于 150 GPa。这表明纳米颗粒的高刚度对纳米复合材料的模量没有起主要作用，应高度重视纳米颗粒的分散/聚集/团聚。

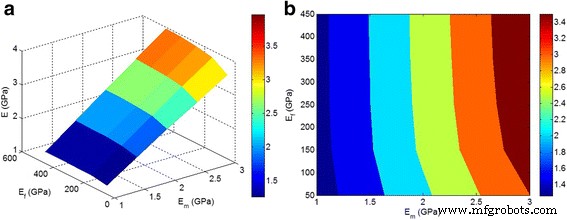
一 , b “E”的影响 m”和“E f” 由方程预测的模量。 10-11 平均ϕ f =0.02, z =0.3，并且 y =0.5

结论

建议采用两步法来确定聚集/附聚纳米颗粒对聚合物纳米复合材料杨氏模量的影响。应用 Paul 和 Maxwell 模型来计算聚集/附聚和有效基质相的模量。假设聚集/附聚参数正确，建议方法的预测与不同样品的实验数据显示出良好的一致性。因此，本方法可以为聚合物纳米复合材料中纳米颗粒的聚集/附聚给出可接受的结果。纳米颗粒的聚集/团聚显着降低了杨氏模量，而纳米颗粒的精细分散产生了高模量。在最小的“z ” 和 “y ”参数，这证实了纳米粒子的良好分散/分布在纳米复合材料的模量中的积极作用。然而，模量随着“y ”参数增加。此外，还发现纳米粒子的优异特性如高模量不足以实现聚合物纳米复合材料的最佳性能。因此，纳米颗粒在聚合物基体中的分散/分布取决于聚合物与纳米颗粒之间的界面相互作用/粘附以及加工参数，应引起高度关注。