磁性纳米粒子组装中的相互作用

背景

磁热疗 [1,2,3,4] 是当代与癌症治疗相关的生物医学研究中最有前途的方向之一。磁性纳米粒子在交变外磁场中发热的性能受多种因素影响，如其几何和材料参数、介质中纳米粒子的浓度以及交变磁场的频率和幅度。本文从理论上研究了磁偶极子相互作用对交变磁场中磁性纳米粒子组装体的比吸收率 (SAR) 的影响。氧化铁纳米粒子似乎最有希望用于磁热疗 [2,3,4,5]，因为它们具有生物相容性和生物可降解性，并且可以使用临床 MRI 在人体中检测到。在这项研究中，我们考虑了具有典型氧化铁纳米粒子磁性参数的纳米粒子组装。最近发现 [4, 6] 嵌入生物环境中，例如嵌入肿瘤中，磁性纳米颗粒与周围组织紧密结合。因此，在交变外磁场的影响下，磁性纳米粒子作为一个整体的旋转受到很大的阻碍。在这种情况下，布朗松弛并不重要 [4]。因此，只需要考虑在交变磁场和热波动影响下的粒子磁矩的运动。此外，必须考虑粒子之间磁偶极相互作用的影响。后一种效应尤其重要，因为生物介质中的磁性纳米颗粒倾向于团聚 [2, 4, 7]，形成具有分形 [8, 9] 几何结构的纳米颗粒的致密聚集体。

参考文献 详细研究了热波动对交变磁场中磁性纳米粒子稀释组件中散热的影响。 [10,11,12,13]。特别是，已经表明 [10] 这种组装的 SAR 基本上取决于平均纳米颗粒直径，以及其他因素。对于稀释的纳米粒子组件，详细计算 [10] 允许人们在给定的粒子磁性参数和给定的交变磁场的振幅和频率下确定纳米粒子的最佳直径。通过对纳米颗粒的几何和磁性参数进行最佳选择，预测了 1000 kW/kg 数量级的非常高的 SAR 值 [10, 11]。值得注意的是，许多实验中报告的 SAR 值 [14,15,16,17] 与上述理论估计值非常接近。同时，在许多实验 [5, 18,19,20,21] 中，测量到的 SAR 值显着降低~ 20–50 kW/kg。这一事实很可能是由于磁性纳米粒子致密组装中强磁偶极相互作用的影响所致。

事实上，实验表明 [22, 23] 磁性纳米粒子密集组装中的 SAR 基本上取决于测试样品的纵横比，即样品长宽比。这是磁偶极子相互作用对纳米粒子组件对交变外部磁场的响应的影响的间接证据。最近的一些理论和实验研究已经研究了磁偶极子相互作用对磁性纳米粒子组装能量吸收率的影响 [7, 24,25,26,27,28,29,30,31,32 ,33,34,35,36,37,38]。然而，考虑到纳米颗粒在生物介质中分布的分形性质 [8, 9]，似乎有必要进行进一步的研究。

为了清楚地看到磁偶极子相互作用的影响，在本文中，我们首先计算了非相互作用氧化铁纳米粒子组件的 SAR。为了研究磁偶极子相互作用的影响，我们对 Landau-Lifshitz 随机方程 [13, 39,40,41] 进行了数值求解，该方程同时考虑了粒子磁矩的热波动和磁偶极子相互作用的存在簇的纳米粒子之间。考虑了两种类型的磁性簇，通常随机分布在刚性介质中的纳米粒子的随机 3D 簇和通常出现在细胞内空间内的纳米粒子的分形簇。请注意，在簇内，纳米颗粒通过强磁偶极相互作用耦合。同时，对于团簇的稀集，团簇之间的磁相互作用可以忽略不计。

磁偶极子相互作用对随机 3D 团簇的稀组装特性的影响表明主要由纳米颗粒堆积密度 η 决定 =N p V /V cl , 其中 N p 是簇中的平均粒子数，V 是纳米粒子的体积，V cl 是簇体积。当 3D 簇的堆积密度在所研究的堆积密度范围内增加时，滞后回线的面积和组装 SAR 显着减小，0.005 ≤ η <0.4。对于磁性纳米粒子的分形簇，除了显着降低 SAR 外，最大吸收率通常会转移到较小的粒径。还发现分形簇的 SAR 随纳米颗粒表面非磁性壳层厚度的增加而显着增加。这种效应可能对磁性纳米粒子组件在磁热疗中的应用具有重要意义。

数值模拟

非相互作用纳米粒子

首先提醒非相互作用超顺磁性纳米粒子在交变磁场中的组装行为是有益的。它使人们能够清楚地看到磁偶极子相互作用对组装特性的影响。基于由 W.F. 推导出的 Fokker-Planck 方程。 Brown [39]，对于种群数n，可以得到一个近似的动力学方程[10] 1(t ) 和 n 2(t ) 单轴超顺磁性纳米粒子的两个势阱

在这里，τ 1(T ) 和 τ 2(T ) 是给定温度下相应的弛豫时间 T 分别为第一和第二势阱。弛豫时间τ 1(T ) 和 τ 2(T ) 主要取决于相对于粒子易各向异性轴的外加磁场的幅度和方向（参见参考文献 [10] 中的附录）。迭代过程可用于计算井人口数n 1(t ) 和 n 2(t ) 交变磁场的几个周期。在交变磁场中获得粒子的静止磁滞回线就足够了。为此，可以对还原粒子磁化强度沿磁场方向的分量使用近似关系

这里，θ 0 为外磁场相对于粒子易各向异性轴的夹角，θ min,1 和 θ min,2 是势阱最小值的位置，作为减小的外加磁场的函数，h e (t ) =H 0sin(ωt )/H 一 , 其中 ω =2πf 是角频率，H 一 是粒子各向异性场。为了获得随机取向的独立纳米粒子组装的磁滞回线，有必要平均减少的磁化强度 m h (t ) 在磁场方向上。值得注意的是，近似解析解的准确性，方程。 Fokker-Planck 方程的 (1), (2), 已经通过与非相互作用磁性纳米粒子的随机 Landau-Lifshitz 方程的数值解直接比较得到验证 [10]。

纳米粒子簇

为了研究磁偶极子相互作用对交变磁场中相互作用的磁性纳米粒子组件的比吸收率的影响，在本文中，我们研究了超顺磁性纳米粒子的常用 3D 簇和分形的稀释组件的行为簇 [8, 9] 通常出现在载有精细磁性纳米粒子的生物介质中。

图 1a 中示意性显示的准球形 3D 纳米粒子簇的特征在于其半径 R cl ，以及纳米粒子的数量，N p>> 1，在其体积内。假设纳米颗粒具有几乎相同的直径 D , 以及它们的中心 {r 我 }, i =1, 2,.. N p ，随机分布在簇体积中。我们还假设粒子涂有薄的非磁性壳，因此簇的相邻纳米粒子之间不存在交换相互作用。正如我们上面提到的，这种 3D 簇的特征在于纳米颗粒的堆积密度 η =N p V /V cl .这是分布在簇体积中的磁性材料的总体积。可以通过关系 D 定义簇的纳米粒子之间的平均距离 av =(6V cl /πN p ) ^1/3 .然后，纳米颗粒堆积密度由 η 给出 =(D /D av ) ³ .

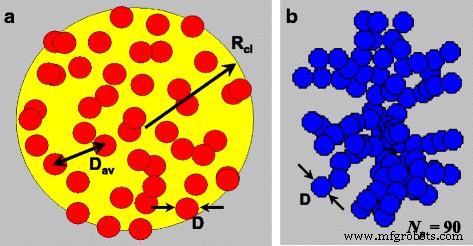
单域纳米粒子的准球形随机 3D 簇的几何形状 (a ) 和分形簇 (b ) 分形描述符 D f =2.1 和 k f =1.3

对于完全随机的 3D 簇的组装，纳米粒子的易各向异性轴的方向 {e 我 }, i =1, 2, .. N p , 在单位球体上随机且独立地选择。或者，人们可以假设在静磁相互作用影响下溶液中形成簇的过程中，纳米粒子易各向异性轴方向的分布发生了一定的相关性。描述这种部分有序簇的一种可能性是假设纳米粒子的易各向异性轴均匀分布在立体角 θ <θ 最大 , 在球坐标中。

具有给定数量粒子的随机 3D 簇 N p 直径D 在本研究中创建如下。首先，我们生成了足够密集且近似均匀的 N 集合 随机点{ρ 我 } 在半径为 R 的球形体积内 cl , 使得 |ρ 我 | ≤ R cl 对于所有生成的点，i =1, 2... N , N>> N p .第一个纳米粒子的中心被放置在第一个随机点 r 1 =ρ 1. 然后，所有坐标为|ρ的随机点 我 –r 1| ≤ D 从随机点的初始集合中删除。在此操作之后，剩余的一组随机点中的任何点都可以用作第二个纳米粒子的中心。例如，可以简单地将 r 2 =ρ 2. 下一步，删除坐标满足不等式|ρ的所有随机点 我 –r 2| ≤ D .重复这个过程直到所有N p 纳米粒子中心位于簇体积内。结果，所有随机纳米粒子中心都位于半径 R 的球体内 cl , 所以 |r 我 | ≤ R cl , i =1, 2,... N p .此外，没有一个纳米颗粒与相邻的纳米颗粒直接接触。该算法使人们能够构建磁性纳米粒子的随机准球形 3D 簇，以获得中等值的纳米粒子体积分数 η <0.5.

对于给定的一组初始参数，即 D , R cl , 和 N p , 各种随机 3D 簇因纳米粒子中心坐标集 {r 我 } 和方向 {e 我 } 粒子易各向异性轴。然而，计算表明，在极限N p>> 1，随机变量{r的不同实现得到的滞后回线 我 } 和 {e 我 } 彼此之间仅略有不同。为了表征随机纳米粒子簇的稀释组装的行为，有必要计算在足够多的随机簇实现上平均的组装滞后回线。发现在极限N p>> 1，即使在初始参数固定值D的随机簇的20-30个独立实现上平均，簇组装的平均滞后回线也具有相当小的离散度 , R cl , 和 N p .

单域纳米粒子的分形簇的几何特征 [42, 43] 由分形描述符 D f 和 k f .根据定义，纳米粒子的总数N p 在分形簇中由关系 \( {N}_p={k}_f{\left(2{R}_g/D\right)}^{D_f} \) 给出，其中 D f 是分形维数，k f 是分形前置因子，R g 是回转半径。它是通过粒子中心与聚集体几何质量中心之间距离的均方定义 [43]。在本文中，使用著名的 Filippov 等人的算法 [43] 创建了具有各种分形描述符的分形簇。作为一个例子，图 1b 显示了具有分形描述符 D 的分形簇的几何结构 f =2.1 和 k f =1.3 由 N 组成 p =90 个单域纳米粒子。从几何上看，3D 和分形簇之间的主要区别似乎在于，在后一种情况下，每个纳米粒子至少有一个相邻粒子位于纳米粒子中心之间的最近可能距离处，该距离等于纳米粒子直径 D .

i 的单位磁化矢量 \( {\overrightarrow{\alpha}}_i \) 的动力学 - 团簇的第一个单域纳米粒子由随机朗道-利夫希茨 (LL) 方程确定

其中 γ 是旋磁比，κ 是现象学阻尼参数，γ 1 =γ /(1+κ ² ), \( {\overrightarrow{H}}_{ef,i} \) 是有效磁场， \( {\overrightarrow{H}}_{th,i} \) 是热场。作用在单独的纳米颗粒上的有效磁场可以计算为总簇能量的导数

团簇的总磁能W =W 一 + W Z + W 米 是磁晶各向异性能量的总和 W 一 , 塞曼能量 W Z 粒子在外加磁场中的能量 \( {\overrightarrow{H}}_0\sin \left(\omega t\right) \)，以及粒子相互磁偶极相互作用的能量 W 米 .

对于具有单轴型磁各向异性的近球形纳米粒子，其磁晶各向异性能量由下式给出

其中 e 我 是 i 的易各向异性轴的方向 - 簇的第一个粒子。塞曼能量 W Z 外加磁场中簇的分布由下式给出

接下来，对于球形均匀磁化的纳米粒子，团簇的静磁能可以表示为位于粒子中心 r 的点相互作用偶极子的能量 我 集群内。则磁偶极相互作用能为

其中 n ij 是沿连接 i 中心线的单位向量 -th 和 j -th个粒子。

因此，作用在 i 上的有效磁场 - 簇的第-个纳米粒子由

其中 H 一 =2 K /M s. 是粒子各向异性场。

热场，\( {\overrightarrow{H}}_{th,i} \), i =1, 2...N p , 作用于簇的各种纳米粒子在统计上是独立的，每个纳米粒子的组分具有以下统计特性[39]

在这里，k B 是玻尔兹曼常数，δ αβ 是克罗内克符号，δ (t ) 是 delta 函数。

求解随机微分方程的过程。 (3)、(8)和(9)在参考文献中有详细描述。 [13, 40, 41]。

结果与讨论

非相互作用的氧化铁纳米颗粒

考虑一个平均直径为 D 的超顺磁性纳米粒子的稀释组合 .假设粒子在周围介质中紧密堆积，并且它们的易各向异性轴在空间中随机取向。这种组件在交变磁场中的磁滞回线 H =H 0sin(ωt ) 可以计算 [10] 使用方程。 (1) 和 (2)。这种方法由于其简单性，可以根据交变磁场的频率和幅度对各种颗粒尺寸的组装磁滞回线进行详细计算。在进行的计算中，根据实验数据 [2,3,4,5,6]，氧化铁纳米颗粒的饱和磁化强度假定为 M s. =70 Am ² /kg，磁各向异性常数为 K =10 ⁴ 焦/米 ³ .组装温度T =300 K，纳米颗粒直径在 D 范围内 =10–30 纳米。这些参数对于在氧化铁纳米颗粒上进行的实验来说似乎很典型。

图 2 显示了在固定振幅交变磁场 H 下，不同频率下氧化铁纳米颗粒的非相互作用组件的 SAR 0 =8 kA/m。可以看出，对于磁热疗特有的频率范围，f =200–500 kHz，SAR 对于直径 D 的氧化铁纳米粒子的组装具有最大值 =20–21 纳米。值得注意的是，即使在交变磁场的相对中等幅度下，如果纳米颗粒直径选择正确，组装 SAR 也能达到足够高的值，350-450 kW/kg。

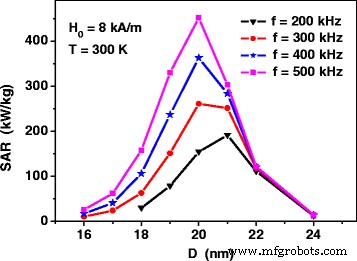
铁氧化物纳米粒子的非相互作用组装的比吸收率，通过方程获得。 (1)和(2)，作为交变磁场不同频率下平均粒径的函数

然而，实验测量的铁氧化物纳米粒子组装的 SAR 值通常显着低于 [18,19,20,21] 这些理论值。正如我们将在下一节中看到的，这个事实可以解释为 [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]强磁偶极相互作用对磁性纳米粒子致密组装的影响。

3D 集群的组装

现在考虑具有在空间中随机取向的单个纳米粒子的简单各向异性轴的 3D 随机簇的稀释组件的滞后回线。如图 2 所示，对于非相互作用的氧化铁纳米粒子的组装，交变磁场中能量吸收的峰值对应于直径 D 的粒子 =20 纳米。因此，我们首先计算了粒子直径 D 的 3D 簇组装的滞后回线 =20 nm。

图 3a 显示了组装滞后回线的演变取决于纳米粒子中心之间的平均距离 D av 在粒径D的固定值 .交变磁场的频率和幅度固定在f =400 kHz 和 H 0 =8 kA/m，分别。簇中的粒子数等于N p =40。计算在 T 进行 =300 K，磁阻尼常数取κ =0.5。

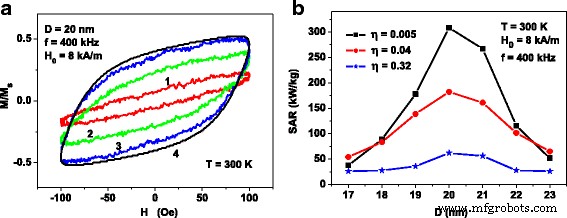
(a ) 直径 D 的氧化铁纳米粒子团簇的稀组装滞后回线的演化 =20 nm，适用于各种比率 D av /D :(1 ) D av /D =1.46; (2 ) D av /D =2.92; (3 ) D av /D =5.84。滞后回线 4 对应于相同直径的非相互作用纳米粒子的组装。它是通过方程计算的。 (1) 和 (2)。 (b ) 作为平均纳米粒子直径函数的 SAR D 用于具有不同堆积密度的纳米粒子簇的稀释组装η

显然，簇的纳米粒子之间平均距离的减小导致簇内磁偶极相互作用强度的增加。注意对于 N p =40，比率 D av /D 图 3a 中指定的对应于簇填充密度 η =0.005、0.04 和 0.32，相应地。可以在图 3a 中看到，作为参数 η 的函数，磁滞回线面积迅速减小 .为了比较，图 3a 还显示了滞后回线 4，为非相互作用粒子的集合计算，即在极限 D av /D → ∞, N p =const，使用方程。 (1)和(2)。

可以看出，磁滞回线 3 (η =0.005) 在图 3a 中结果接近于非相互作用纳米粒子组装的滞后回线。因此，在η的情况下 ≤ 0.005 可以忽略簇内纳米粒子的磁偶极相互作用。然而，对于η ≥ 0.04 磁偶极子相互作用对随机 3D 簇组装的特性有显着影响。对于频率 f 也获得了组装磁滞回线的类似演变 =300 和 500 kHz，分别。

图 3a 所示的磁滞回线是针对不同的比率 D 计算的 av /D , 但对于簇 N 中固定数量的纳米粒子 p =40。然而，详细的计算机模拟表明，如果粒子数 N p>> 1，以及簇的半径 R cl 改变使纳米颗粒堆积密度 η 保持不变。因此，随机3D团簇稀组装的滞后回线主要取决于团簇堆积密度η .

图 3b 显示了不同 η 的氧化铁纳米颗粒随机簇的组装的 SAR 值。组件的 SAR 计算为 [10] 为 SAR =M s FA /ρ , 其中 A 是变量 (M /M s. , H ), ρ 是氧化铁纳米颗粒的密度，假定为 ρ =5 × 10 ³ 公斤/米 ³ .如图 3b 所示，SAR 作为 η 的函数减小 由于簇内磁偶极子相互作用强度的增加。同时，组装SAR对平均粒径的依赖性仍然存在，尽管变得不那么明显。

对于 η 的小值 ≤ 0.005，3D 簇随机组装的 SAR 实际上与非相互作用纳米粒子组装的 SAR 一致，如图 2 所示。另一方面，当簇堆积密度增加到 η =0.32。然后，它变得接近典型的 SAR 值 ~ 50–100 kW/kg，这是在使用氧化铁纳米粒子组件的许多实验 [5, 18,19,20,21] 中获得的。

分形簇的组装

对具有各种分形描述符的纳米颗粒的分形簇的稀释组件进行了类似的计算。如图 4 所示，对于纳米颗粒的分形簇，相对于非相互作用纳米颗粒的组装，作为粒径函数的 SAR 也显着降低。然而，与 3D 簇的组装相反，SAR 的峰值系统地向更小的粒子直径移动，除了分形维数 D f =2.7，这接近于具有 D 的 3D 集群的情况 f =3.0。值得注意的是，对于非最佳纳米颗粒直径，例如，对于直径 D 的纳米颗粒 ≤ 17 nm，磁偶极子相互作用的影响导致相对于非相互作用纳米粒子组装的 SAR 增加，因为对于直径 D ≤ 17 nm。

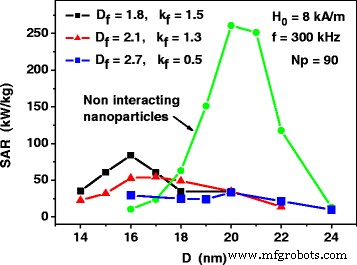
SAR 作为平均纳米颗粒直径的函数 D 用于具有各种分形描述符的纳米颗粒分形簇的稀释组装。非相互作用纳米粒子组装的 SAR 是通过方程计算的。 (1)和(2)

图 4 所示的计算是假设存在厚度为 t 的非磁性薄壳而进行的 嘘 =1 nm 在磁性纳米粒子的表面。这防止了分形簇的纳米粒子直接交换相互作用。显然，随着纳米颗粒上磁核之间的平均距离增加，非磁性壳厚度的增加降低了最近纳米颗粒的磁偶极相互作用强度。图 5 表明增加非磁性壳层厚度是提高纳米颗粒分形簇组装 SAR 的适当方式。即，对于足够大的非磁性壳厚度，SAR 对粒径的依赖性类似于弱相互作用磁性纳米粒子的依赖性。 This fact may be important for the application of magnetic nanoparticle assemblies in magnetic hyperthermia.

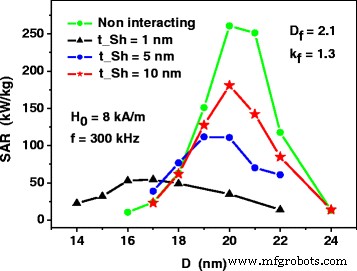
The dependence of the SAR of dilute assembly of fractal clusters on the thickness t Sh of the non-magnetic shells at the surface of the nanoparticles. The SAR of the assembly of non-interacting nanoparticles is calculated by means of Eqs. (1) and (2)

结论

The main conclusion of this study is that the SAR of a dilute assembly of clusters of magnetic nanoparticles in alternating magnetic field is significantly reduced with increasing of the intensity of magneto-dipole interaction in the clusters. For usual 3D clusters of nanoparticles, the intensity of the magneto-dipole interaction can be characterized by dimensionless packing density, η  = N p V /V cl  = (D /D av ) ³ . The latter determines the average distance between the nanoparticles of the cluster. The calculations show that for the assembly of random 3D clusters, the energy absorption peak, which for iron oxide nanoparticles corresponds to particles with average diameter D  = 20 nm, is reduced about six times when the packing density increases from η  = 0.005 up to η  = 0.32. The dependence of the assembly SAR on the mean nanoparticle diameter is retained with increase of η , but becomes less pronounced.

For dilute assemblies of fractal clusters of magnetic nanoparticles, the SAR values also decrease several times irrespective on the fractal descriptors of the assembly. In addition, the peak values of SAR are shifted systematically to smaller particle diameters, as a rule. It is important to note, however, that the increase of the non-magnetic shell thickness at the nanoparticle surfaces restores the SAR values close to that of the assembly of weakly interacting nanoparticles. This fact can be important for various biomedical applications of magnetic nanoparticle assemblies.

The model considered in this paper takes into account the geometrical structure of nanoparticle assemblies observed experimentally in biological media [4, 8, 9] (in particular in tumors), i.e., the agglomeration of nanoparticles in a sufficiently dense fractal clusters of different sizes, with different numbers of nanoparticles in the clusters. The stochastic LL Eq. (3) accurately describes the real dynamics of the magnetic moments of nanoparticles taking into account both the magneto-dipole interaction between the particles and the effect of thermal fluctuations. The cluster model studied allows obvious generalization that can make it more practical. First, it is necessary to take into account the size distribution of magnetic nanoparticles in the assembly. Second, in some cases exchange interaction may exist between neighboring nanoparticles of the cluster if they are in direct atomic contact.

The theoretical results obtained in this study seem to be in a satisfactory agreement with recent experimental data [35] for iron oxide nanoparticles of optimal diameters. Indeed, according to Ref. [35], the SAR of the iron oxide nanoparticles increases with the average diameter of the nanoparticles and peaks for nanoparticles with mean diameter D  = 20–21 nm. In addition, the SAR decreases [35] with a decrease in the average distance between the nanoparticles due to increasing intensity of the magneto-dipole interaction.

Unfortunately, in some experimental studies [5, 21] carried out to optimize the properties of magnetic nanoparticles for use in magnetic hyperthermia, often do not take into account the theoretical predictions [10, 11] about significant dependence of the assembly SAR on the characteristic size of the magnetic nanoparticles. As shown in this paper, this dependence can be substantial even for rather dense nanoparticle assemblies. From a theoretical point of view, it is obvious [10] that the assembly of iron oxide nanoparticles with very small, D  ≤ 10 nm, or too big, D  ≥ 30 nm diameters can hardly provide a sufficiently high SAR values for typical for magnetic hyperthermia frequencies, f  = 200–600 kHz, and magnetic field amplitudes H 0 ~ 8 kA/m. The creation of mono-crystalline iron oxide nanoparticles with sharp size distribution near the optimal diameter has to be promising for application in magnetic hyperthermia.