表面对纳米通道中石油运输的影响：分子动力学研究

背景

受世界能源需求不断增长和常规能源过度消耗的启发，非常规页岩油的开发因其储量大、生产潜力大而受到广泛关注[1]。页岩油是成熟有机页岩油的简称，是非常规能源项下最具代表性的能源。尽管世界已知的页岩油总资源量比剩余常规原油高出 3 倍以上 [2]，但据估计，页岩油的总可采储量远低于储量。此外，油页岩已被开采约200年，但目前页岩油的开发利用受到很大限制。所有这些都表明，受限于纳米通道的页岩油难以提取[3]。油页岩通道尺寸宽度为 2~100 nm [4, 5]，产生较大的比表面积和多种表面效应。在流体与基体表面相互作用的影响下，可能会引起许多新的物理现象，例如，水在纳米管内部流动比在经典宏观管中快得多 [6, 7]，发现孔隙碳电容异常增加尺寸小于 1 nm [8]，随着宽度的减小，碳纳米管中的水亲和力从疏水性变为亲水性 [9]。位于油页岩中，流体与页岩基质的表面相互作用强，流体表现出许多不同于宏观通道中的特征，如密度分布、润湿性和扩散系数[10,11,12]，导致流体通过这种纳米通道与宏观通道中的流体传输特性不同。 Chen 等人使用分子动力学 (MD) 模拟。研究了模型碳纳米管内水的传输行为，发现流体和通道之间的剪切应力是尺寸敏感的，他们还通过甘油中的纳米多孔碳的实验验证了模拟结论 [13]。薛等人。考虑了在气驱驱动力下癸烷在二氧化硅纳米通道中的流动，他们发现油和基质之间的初始压力和相互作用能在油滴置换中起着重要作用[14]。王等人。通过MD模拟模拟了石英狭缝中辛烷的流动，他们发现速度随着外力、通道宽度和温度的增加而增加，他们还发现表面效应可以主导纳米通道中油的输送减小通道宽度 [15]。如上所述，流体与纳米通道之间的强表面相互作用对流体在纳米通道中的流动具有至关重要的影响。然而，关于表面性质对纳米通道内输油动力学机制影响的系统研究很少。了解表面效应对纳米通道中页岩油输运的影响，对促进页岩油的开发利用具有重要意义。

在这项工作中，我们使用 MD 模拟研究了纳米通道中石油运输的动力学机制，并证明了油分子与通道表面之间的表面相互作用、通道表面的粗糙度以及油分子之间的相互作用都对质心有很大影响(COM) 纳米通道中的油置换。该结论不仅将为能源领域提供光明的前景，而且将为环境、生物医学、化学、能源和工业应用等广泛的自然科学提供启示，包括蛋白质易位、混合物的膜分离和通道电池[16,17,18,19,20]。

方法

所有 MD 模拟均由 Material Studio (Accelrys Inc.) 软件中的 Discover 代码执行。用于原子模拟研究的凝聚相优化分子势 (COMPASS) 用于描述原子间相互作用。 COMPASS 力场是基于 ab initio 的通用全原子力场，并使用凝聚相中分子的大量数据进行参数化。力场势可表示为：

在上面的等式中，E 价是指价（或键）能，通常由键拉伸、价角弯曲、二面角扭转和反转等对角线项来解释。 E 交叉项是指交叉项能量，它考虑了附近原子引起的键或角度扭曲等因素，以准确再现分子的动态特性。还有 E 非键是指非键能，它解释了非键原子之间的相互作用，主要来自范德华 (vdW) 相互作用和静电相互作用。这三项可以表示为

其中 b 和 b '是两个相邻键的键长，θ , φ , 和 χ 分别是两键角、二面扭转角和平面外角。 q 是原子电荷，ε 是介电常数，r ij 是 i -j 原子间隔距离。 b 0, K 我 (i =2 − 4), θ 0, H 我 (i =2 − 4), \( {\phi}_i^0 \) (i =1 − 3), V 我 (i =1 − 3), \( {F}_{b{ b}^{\prime }} \), \( {b}_0^{\prime } \), \( {F}_{\theta { \theta}^{\prime }} \), \( {\theta}_0^{\prime } \), F bθ , F bφ , \( {F}_{b^{\prime}\theta} \), F 我 (i =1 − 3), F θφ , \( {K}_{\phi \theta {\theta}^{\prime }} \), A ij 和 B ij 符合量子力学计算，并在 Materials Studio 的 Discover 模块中实现。使用 Lennard-Jones 势来描述油分子、油分子和纳米通道之间的分子间相互作用 [14, 21, 22]。选择截止距离 15.5 Å 来计算 vdW 相互作用，Ewald 方法和基于原子的方法分别用于计算静电相互作用和 vdW 相互作用。该系统是在恒定体积和恒定温度下计算的，即采用 NVT 系综。温度为 298 K，选择 Andersen 恒温器方法将系统控制在热力学温度。在所有三个维度上都施加了周期性边界条件。每 5 ps 采集一次数据，并记录完整的准确轨迹。

在大多数页岩地层中，岩石矿物的主要成分是二氧化硅 [23,24,25]。因此，在我们的模拟中选择二氧化硅表面作为油页岩表面。二氧化硅的初始晶格来自 Material Studio 软件的数据库。 (0 0 1)面被解理，然后细化矩形面。每个基板表面的尺寸为1.5 × 7 × 0.85 nm ³ .沿 z 的分离通道 -轴是在两个基板表面之间创建的，如图 1a 所示。通道表面完全被羟基修饰以代表地质条件[26]。

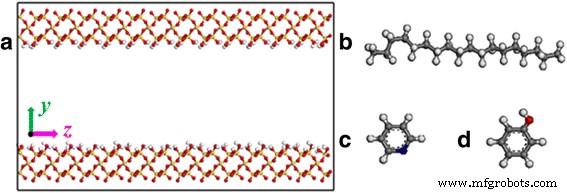
一 二氧化硅纳米通道模型的表示。 b的分子结构 十八烷，c 吡啶和d 苯酚。原子的颜色代码：红色 , 氧气; 白色 , 氢; 黄色 , 硅; 灰色 ， 碳;和蓝色 , 氮

系统的初始配置是由填充在硅胶通道内的十八烷分子构建的。四十个十八烷分子插入宽度为 2 nm 的狭缝通道，导致密度为 0.8 g/cm ³ .我们还研究了页岩油的另外两种成分吡啶和苯酚分子的输运特性，以研究油分子对纳米通道中输油的影响。十八烷、吡啶和苯酚的结构从 Material Studio 软件的数据库中提取，如图 1b-d 所示。为保证油的密度相似，我们模拟中宽度为4和6 nm的通道中吡啶分子、苯酚分子和十八烷分子的数量分别为407、344、80和120。

使用 Discover Minimization，我们首先执行能量最小化来优化系统，使系统达到良好的平衡。使用 500 ps 预运行执行平衡模拟，以确保系统已达到稳定状态。然后通过平行于通道表面（沿着 z -axis) 到所有油分子，以促进通过通道的运输，这通常用于模拟流体运输 [27,28,29]。我们在此注意到 MD 模拟的一个限制是，由于 MD 计算所需的时间，与环境设置中的力相当的力是不切实际的；因此，我们施加的力产生的平均值为 3.1 × 10 ⁻¹⁴ 每个原子上的 N。大力的目的是在有限的模拟时间内获得更精确的输油数据。

结果与讨论

通道宽度的影响

我们首先关注通道宽度对石油输运特性的影响。在外力的作用下，流经通道横截面的原子数量随着模拟时间的推移逐渐增加（附加文件 1：图 S1，支持信息）。油分子被拉动约 2 ns。如图 2d-f 所示，随着通道宽度的增加，2 ns MD 模拟后油的位移距离更大。为了定量描述沿通道轴的油位移，我们计算了 2 ns 后油在其初始位置和最终位置之间的 COM 位移。 MD 模拟及其沿 z 的初始位置 -轴和质心是根据原子坐标的质量加权平均值定义的。

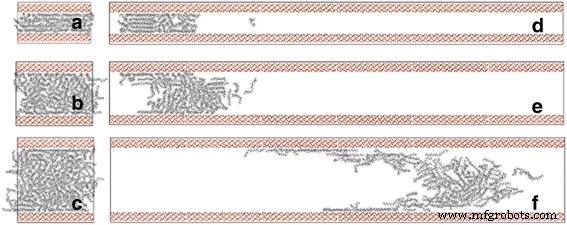
力驱动十八烷分子在宽度为a的二氧化硅通道中传输过程的初始模型 2、b 4、c 6 nm，以及 d 中十八烷分子的快照 2、e 4、f 2 ns 时的 6 nm 通道

在图 3 中，我们展示了 2 ns MD 模拟后的驱油情况。结果表明，在对每​​个原子的拉力相同的情况下，油在2 nm通道的COM位移仅为0.85 nm，远小于6 nm通道。这表明通道越窄，对油分子的吸附约束越明显。

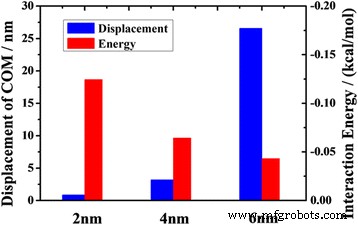
2 ns时油的COM位移和油与通道之间的平均相互作用能与通道宽度的关系

为了明确吸附约束的影响，我们计算了油分子与底物之间的平均相互作用能。平均相互作用能计算如下：

其中 E 平均相互作用是油分子与底物之间的平均相互作用能； E total 代表整个系统的总能量； E 油和E 底物分别是油组分和底物组分的能量；和 N 是油分子的总原子数 [14, 30, 31]。图 3 表明，随着平均相互作用能的增加，驱油量减少。很明显，油分子和通道之间的吸附随着相互作用能的增加而增长。通道的强吸附抑制了狭窄通道中的石油输送。从图 3 所示的数据我们发现，当相互作用能增加 3 倍时，驱油量减少了 30 倍以上。这表明油的运输受油分子与底物相互作用的影响很大。然而，这种影响随着沟道宽度的增加而减弱。纳米通道对石油输送的尺寸效应比微通道更明显（附加文件 1：图 S2）。因此，降低油分子与底物的相互作用能是增强纳米通道内油输送的关键因素。

从图 2 可以看出，纳米通道表面附近有明显的分层结构，厚度约为 5 Å。需要说明的是，与通道表面接触的层和通道中心的层分别称为接触层和中心层。显然，在近地表区域发现了有序的油分子层。十八烷分子的取向通常用角度θ来表征 通道表面的法向矢量和由连接十八烷分子末端的两个碳原子的线形成的一些矢量之间的矢量 [15, 29]。每层十八烷分子在 2 ns 时的取向分布如图 4 所示。这里，θ =80 ^o ～ 90 ^o 对应于分子的平行取向，而 θ 的值 =0 ^o ～ 10 ^o 表示分子垂直于通道表面。可以看出，由于强油面相互作用，十八烷分子主要平行于2 nm通道层和4 nm通道和6 nm通道的接触层中的表面（图5b）。对于 4 nm 通道和 6 nm 通道的中心层，十八烷分子没有优先取向，这意味着这些十八烷分子倾向于与通道表面成不同的角度。接触层中排列的十八烷分子对油分子在纳米通道中的传输性能很重要。

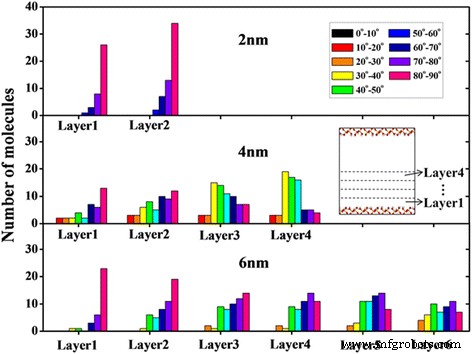
不同通道宽度下各层十八烷分子的取向角分布

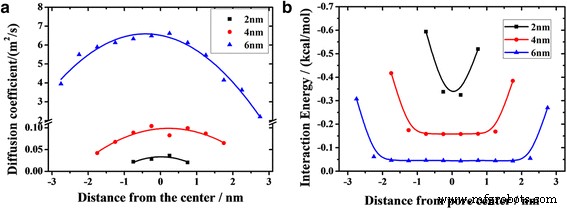
一 不同宽度通道中油的扩散系数分布。 b 油分子与二氧化硅之间平均相互作用能的距离依赖性（带符号）。实线代表拟合函数

接下来，我们通过检查轨迹观察到各个层的启动时间（定义为层位移超过 5 Å 的时间）是不同的。支持信息（附加文件 1：表 S1）中列出的启动时间数据表明，接触层的启动时间随着沟道宽度的减小而增加，这意味着在较窄的沟道中启动接触层移动所需的拉力为比在更宽的通道中所需的更大。此外，中心层的启动时间远早于接触层。

此外，我们发现油的流速随着与通道轴距离的增加而减小，接触层的流速随着通道宽度的减小而减小（图 2d-f）。为了定量描述这些特征，我们研究了远离通道中心的不同位置的油分子扩散系数，该系数是根据均方位移的时间演化获得的

其中 r 我 表示i的位置向量 第 th 个粒子，尖括号表示整体平均值。图 5a 显示了层的扩散系数如何取决于纳米通道中的位置。 4 nm 通道和 6 nm 通道的曲线呈抛物线型，即朝向通道表面，层的扩散系数逐渐减小。 6-nm 通道显示高值和低值之间的最大差异为 4.4 m ² /s，而 2-nm 通道的最小差异为 0.016 m ² /秒。 2nm通道层的扩散系数略有不同，因此油的前表面看起来像一个活塞。此外，我们发现距离通道表面相同距离的层的扩散系数对于各种通道有很大差异（图5a）。例如，6 nm 通道中与下通道表面接触的层的扩散系数为 3.9 m ² /s，而在 2 nm 通道中仅为 0.02 m ² /秒。这意味着距离通道表面相同距离的层的流速随着通道宽度的增加而增加。

在图 5b 中，我们展示了远离通道中心和通道的不同位置的油分子之间的平均相互作用能。由于底物对1nm范围内的油分子有很强的吸附作用，曲线两端的相互作用能明显较大，并在1nm范围内迅速下降，这也是接触层启动缓慢的原因之一。然而，油分子和通道之间的相互作用能不能充分解释前表面的形状，因为它对于强吸附范围之外的层的值几乎相同。抛物线前表面不仅与油与通道的相互作用有关，而且与油分子之间的相互作用有关。分子间相互作用有助于流体粘度，它在粘弹性流体中的动量传递中起重要作用。由于通道对油的吸附范围约为 1 nm，因此部分油层位于该区域，如图 6 中阴影所示。油与底物之间强烈的表面相互作用阻碍了油层在阴影中的输送。动量从阴影外的层传递到阴影中的层。离开阴影的原子数量随着通道宽度的减小而减少。因此，较少的动量传递到较窄通道中的阴影层。因此，接触层的扩散速度随着沟道宽度的减小而减小。

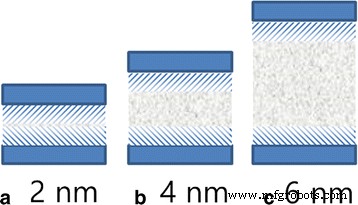
一 , b , c 油与底物的吸附范围示意图

极性的影响

页岩油中始终含有极性油成分，这些极性油成分在油/二氧化硅界面的吸附中起着重要作用[21, 32]，因此了解它们对石油输送的影响至关重要。以苯酚和吡啶为例，我们在4-nm通道中进行模拟，苯酚和吡啶的原子数大约等于4-nm通道中十八烷的原子数。硅胶通道中吡啶、苯酚和十八烷在 2 ns 时的快照如图 7 所示。与十八烷分子相比，苯酚分子和吡啶分子几乎不受拉力驱动。图 8 中的虚线显示了 2 ns MD 模拟后不同油分子的 COM 位移。尽管对每个原子的拉力相等，但十八烷的 COM 位移几乎是苯酚和吡啶 COM 位移的 16 倍。

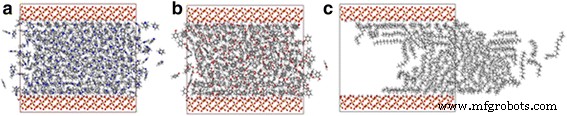
a 的快照 吡啶，b 苯酚和c 2 ns 时在 4 nm 二氧化硅通道中的十八烷传输

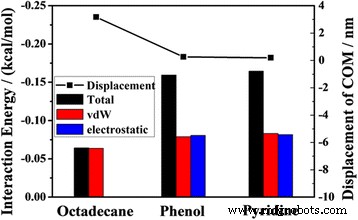
2 ns时油的COM位移和不同组分与通道之间的平均相互作用能（总、vdW和静电）

为了理解这些结果，我们计算了不同组件与通道之间的总相互作用、vdW 相互作用和静电相互作用的能量。图 8 中的直方图说明苯酚（吡啶）和二氧化硅底物之间的总相互作用能大于十八烷和二氧化硅通道之间的总相互作用能。由于十八烷分子是链状的非极性分子，十八烷分子与通道的全部相互作用主要来自vdW相互作用，几乎没有静电相互作用，而vdW相互作用和苯酚（吡啶）与通道之间的静电相互作用的贡献总互动的渠道几乎相同。

为了研究极性对石油输运的影响，我们使用第一性原理模拟计算了三个分子的偶极动量。性能的细节遵循我们之前的工作 [33,34,35,36]。结果表明，十八烷、苯酚和吡啶的偶极动量分别为 0.0322、1.3059 和 2.2449 德拜。这表明在纳米通道中，极性油分子比非极性分子更难被驱动。但油的 COM 排量并不总是随着极性的降低而增加。对于两个极性油分子，苯酚的极性比吡啶的极性弱，但它们的COM位移几乎相等。

材料类型的影响

还比较了由各种材料制成的纳米通道之间油分子的传输特性，包括二氧化硅、金和方解石。图 9 显示了 2 ns 时方解石和金通道中十八烷分子的快照。图9a显示了方解石通道中油分子的明显运输，表明方解石中的十八烷分子也可以被拉力驱动，而金通道中的分子几乎不能移动（图9b）。

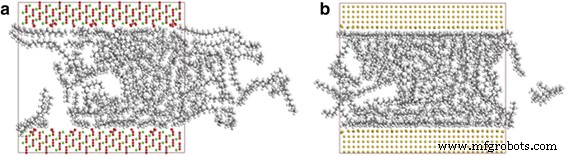
4 nm a 中十八烷传输的快照 方解石通道和b 2 ns 的金通道。原子的颜色代码：绿色、钙；黄色、金色

图 10 显示了十八烷分子在各种材料通道中的 COM 位移以及油与不同材料通道之间的平均相互作用能。二氧化硅通道中油的 COM 排量远大于金通道中的油。这种现象可以用油分子与通道相互作用的影响来解释。油分子和二氧化硅通道之间的平均相互作用比油分子和金通道之间的相互作用要小得多。但对于二氧化硅通道和方解石通道中油分子的运输，该因素并不能充分解释差异。油分子与二氧化硅通道之间的平均相互作用能与油分子与方解石通道之间的平均相互作用能似乎没有太大差异，但两种情况下的 COM 位移却有很大差异。其原因可能与表面原子和表面纹理有关。这些结果表明，油分子与通道之间的相互作用对油的输送有很大影响，但当相互作用能值相似时，纳米通道内的油输送是这些因素之间的竞争。

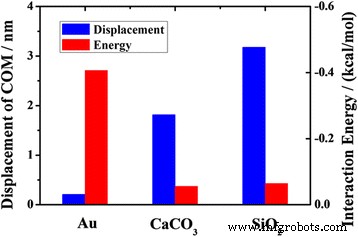
2 ns时油的COM位移及油与不同材料底物的平均相互作用能

表面粗糙度的影响

众所周知，纳米尺寸的表面粗糙度对微尺寸通道内的流体流动几乎没有影响。然而，已经证明纳米尺寸的表面粗糙度对纳米通道中的流体传输有很大影响 [37,38,39]。为了研究粗糙度对十八烷传输的影响，我们通过从基板表面切下少量原子来构建粗糙表面，从而形成一个深度为 d 的空腔 =3 Å（或 6 Å）且在基板表面形成 35 Å 的宽度。裸露的氧原子被氢原子修饰。 3 Å和6 Å空腔分别加入5个和10个十八烷分子，外力相应增加。图 11 显示了在 2 ns 时流过空腔深度为 3 和 6 Å 的粗糙通道的十八烷快照的比较。 We observe that inside every cavity, there are some oil molecules, and their localizations are affected by the cavity, which results in a reduction of velocity values inside the cavity, as well as the velocity of oil molecules nearby. And this becomes more obvious when d  = 6 Å, as shown in Fig. 11b. To quantify the influence of roughness on transportation, we further calculate the COM displacement of oil in rough channels. The COM displacements of oil in channels with 3 and 6 Å depth cavity are 3.95 and 3.07 Å, respectively. When d  = 6 Å, the value of oil displacement is 3.07 Å, which is smaller than the value 3.17 Å of oil molecules in flat channel. Somewhat surprisingly, however, for d  = 3 Å, the displacement is even larger than that in flat channel. We expect that these characters are contributed by two parts:(1) the cavity increases the width of the nanochannel so that the oil molecules have a greater diffusion coefficient according to the above discussion, which facilitates the transportation of oil; (2) the oil molecules in cavity can suppress the transportation of oil molecules nearby and therefore decrease the oil transportation speed. For the oil molecules in channel with d  = 3 Å, the effect of suppression caused by the less oil molecules in cavity is less than the effect of facilitation caused by the width increment. When d  = 6 Å, the diffusion coefficient of oil molecules is further increased; however, more oil molecules are suppressed by the deeper cavity, and the effect of suppression on the transportation of oil molecules is more than that of facilitation, thereby reducing the oil displacement. Because of these complications, we cannot separate these parts and judge how much contribution of each part has on the displacement.

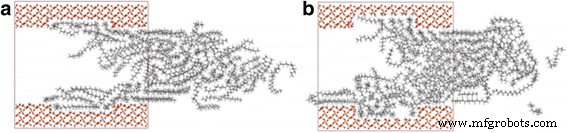
Snapshots of octadecane transportation in rough channel with the cavity depth of a 3 and b 6 Å at 2 ns

结论

In this study, we investigate the mechanism of oil transportation in nanochannels using molecular dynamics simulations. It is demonstrated that the oil displacement in a 6 nm channel is over 30 times larger than that in a 2 nm channel, and the diffusion coefficient of oil molecules at the center of the 6 nm channel is almost two times more than that near the channel surface, due to interaction difference between the oil molecules and channels. Besides, we find that both the polarity of oil molecules and channel component have great effects on the interaction between oil molecules and channel in the channels with same width; the larger the interaction between oil molecules and channel is, the smaller the oil displacement is. Finally, we demonstrate that surface roughness can obviously affect oil transportation in nanochannels. The mechanism by which the cavity structure affects the transportation of oil is an intricate issue, which should be further studied. Our findings would contribute to revealing the mechanism of oil transportation in nanochannels and therefore are very important for design of oil extraction in nanochannels.

缩写

COM:

Center of mass

COMPASS:

Condensed-phase optimized molecular potential for atomistic simulation studies

MD:

Molecular dynamics

vdW:

van der Waals