在硅衬底上设计用于中红外直接带隙发射的应变工程 GeSn/GeSiSn 量子点

背景

最近，通过将 Ge [1, 2] 和 SiGe [3, 4] 与锡合金化来展示直接带隙第 IV 族材料，这激发了大量的研究活动，因为这为实现高效片上光子学和电子学提供了切实可行的机会一体化。事实上，与 L 谷相比，GeSn 合金已显示出超过特定成分的直接带隙，通过 Γ 的更快下降 [5,6,7,8]。虽然报告的结果非常令人鼓舞，但材料特性和应用潜力尚未得到充分探索。实际上，增加基于 GeSn 的半导体激光器的工作波长的主要实际可用路径，朝向与各种气体的吸收线重叠的大气透明窗口 [9]，包括增加 GeSn 层中的 Sn 含量 [10, 11 ]。然而，由于 Ge 和 Sn 之间存在较大的晶格失配 (14%)，保持材料的结晶质量似乎是阻碍这一目标的主要挑战 [12, 13]。增加发射波长并确保更好的载流子限制的潜在有趣解决方案依赖于较低维度的结构，例如纳米线 [14,15,16]、纳米棒 [17] 和量子点 [18]。在特定的直接性标准内，直接带隙带间发射波长理论上限于 4.3 μm [19]。为了克服这些限制，有必要在基于 IV 族的量子结构的概念中引入额外的自由度。这可以通过使用三元 GeSiSn 层 [20,21,22] 作为 GeSn 量子点 (QD) 的周围材料来确保，通过结合适当的 Si 和 Sn 成分提供应变工程的可能性。 因此，在GeSn QD周围使用GeSiSn应变工程层有望提供更大范围的可及直接带隙发射波长。

在此背景下，我们报告了通过改变围绕 GeSn QD 的 GeSiSn 层中的 Sn 成分对直接带隙带间发射波长的应变工程影响的理论研究。

方法

由于二元和三元含 Sn 族 IV 合金与 Ge 之间的带偏移量在实验中未知，因此评估了本工作中涉及的不同 IV 族半导体之间的相对带对齐，相对于 Ge 的价带边缘，使用 D'Costa 等人详述的 Jaros 的带偏移简化理论 [23]。 [24]。已经针对导带和价带边缘评估了由Ge衬底和GeSiSn层之间以及GeSn QD和周围GeSiSn材料之间的晶格失配引起的应变效应。

事实上，导带边缘移动了 \( \delta {E}_c^i \) 和价带移动了 δE v 如方程式所示。 (1)和(2)：

其中 i 表示 L 或 Γ 谷，a c 和 a v 分别是导带和价带变形势，b 是剪切变形势。 \( {\varepsilon}_{xx}={\varepsilon}_{yy}=\varepsilon =\left(\frac{a_s-{a}_{\mathrm{l}}}{a_{\mathrm{l }}}\right) \) 是计划内应变和 \( {\varepsilon}_{zz}=-2\frac{C_{12}}{C_{11}}{\varepsilon}_{xx} \) 是增长方向的应变。 一 s 和 a l 分别为衬底和应变层的晶格参数。 C 11 和 C 12是刚度常数。

二元和三元合金材料参数是通过线性插值从 Ge、Si 和 Sn 的参数导出的。这些参数取自参考文献[11]。

可以通过将相应的应变产生的能量转移添加到方程 1 中给出的无应变材料的带隙来评估与成分相关的应变带隙。 (3) 对于 GeSn 和方程。 (4) 对于 GeSiSn:

其中 b 是表 1 中总结的二元合金的相应带隙弯曲参数。

为了确定载流子的约束状态并推导带间跃迁能量，利用 COMSOL Multiphysics 软件提供的有限元方法在笛卡尔坐标系中求解了单带有效质量薛定谔方程[25]：

E 表示载流子的能量，ψ 是对应的波函数。 米* 是载体的有效质量，ћ 是约化的普朗克常数，\( \overrightarrow{r} \) 是三维坐标向量，V 是载体的限制潜力（频带不连续性）。为了简化 QD 电子结构的计算过程，我们采用了恒定应变近似 [26, 27] 而不是计算成本高的原子模拟方法，显然可以在应变分布剖面中提供更高的精度 [28, 29]。事实上，我们认为压缩应变 QD 中的载流子限制势足够深，以最大限度地减少应变非均匀性对电子限制态的影响 [27]。此外，导带边缘是这项工作中最重要的参数，允许研究带隙直接性，仅因流体静力应变对应变非均匀性较不敏感而移动，尤其是在考虑相对较低的晶格失配时[30].

结果与讨论

由于我们主要关注 GeSn QD 周围应变的影响，因此 QD 的 Sn 成分固定为 28%，GeSiSn 的 Si 成分固定为 35%；因此，该研究侧重于 Sn 阻挡层成分的影响 (x b ) 6 到 22% 之间的变化。 GeSiSn 层或 GeSn QD 中产生的平面应变如图 1a 所示。

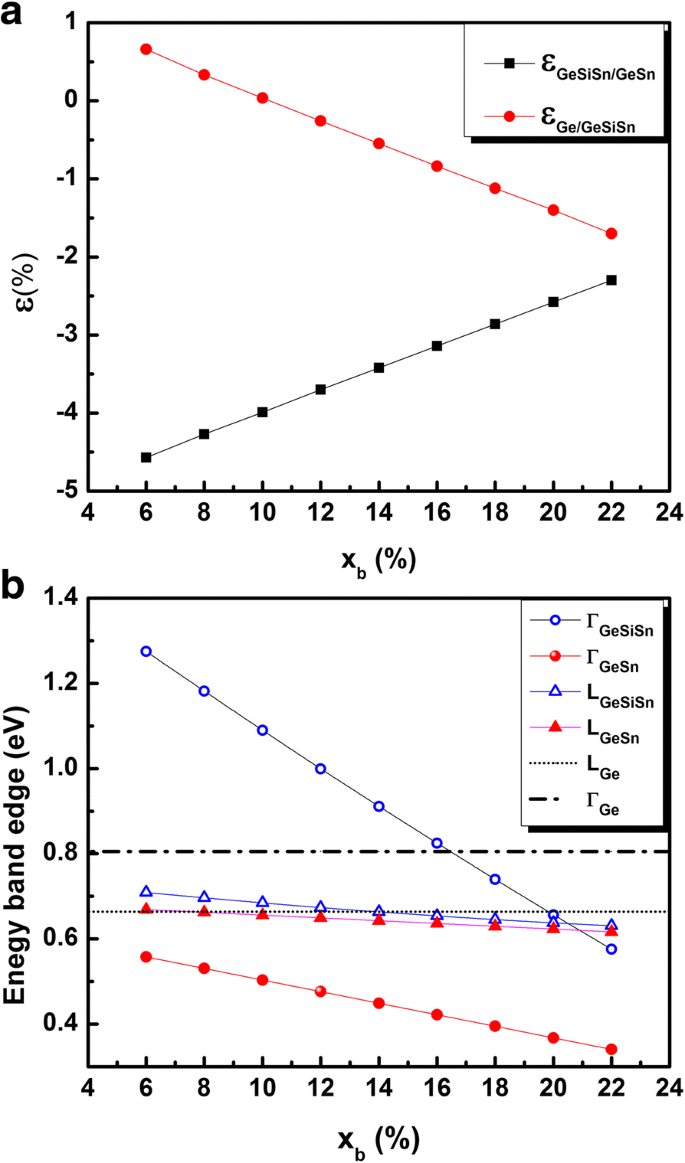
一 Ge0.65-xb 之间的晶格失配 Si0.35Sn xb 和 Ge（实心圆圈）以及 Ge0.72Sn0.28 和 Ge0.65-xb 之间 Si0.35Sn xb （实心方块）作为 x 的函数 b . b Ge0.65-xb 在 L 和 G 谷的能带边缘 Si0.35Sn xb , Ge0.72Sn0.28, 和 Ge 作为 x 的函数 b

GeSiSn 材料二维层中的平面应变在 0.6% (x b =6%) 和 − 1.7% (x b =22%)。我们假设该层保持假形态应变，从而使设计的结构在实验上可实现。 GeSn被选择在GeSiSn周围材料内压缩应变，晶格失配范围从- 2.3到- 4.5%，确保有利于自组织GeSn QD的形成。

图 1b 显示了来自 Ge0.72Sn0.28 和 Ge(0.65-xb )Si0.35Sn xb 作为 x 的函数 b . Ge0.72Sn0.28 材料的 Γ 谷保持在 L 谷之下，证明其在锡阻挡层成分的整个研究范围内属于 I 型。同时，当考虑电子限制时，有效带隙增加并且 QD 尺寸效应变得决定性 [18]，尤其是对于高应变 QD。事实上，在存在量子限制的情况下，应该考虑基态能量而不是 Γ 带的最小值。因此，预计较小尺寸的 QD 在 Γ 谷中具有更高的受限能级，其可能超过 L 谷（和/或 L 谷中的基态电子能级）。因此，研究符合特定直接性标准的量子点尺寸范围很重要。

模型结构如图 2 所示。Ge0.72Sn0.28 QD 被认为具有圆顶形状，圆底直径为 D 范围从 15 到 40 纳米，固定的高径比等于 0.25。 QD 位于 15 纳米厚的 GeSiSn 层内，该层具有 35% 的 Si 成分和可调的 Sn 成分。该结构应该形成在Ge缓冲衬底上并覆盖Ge层。

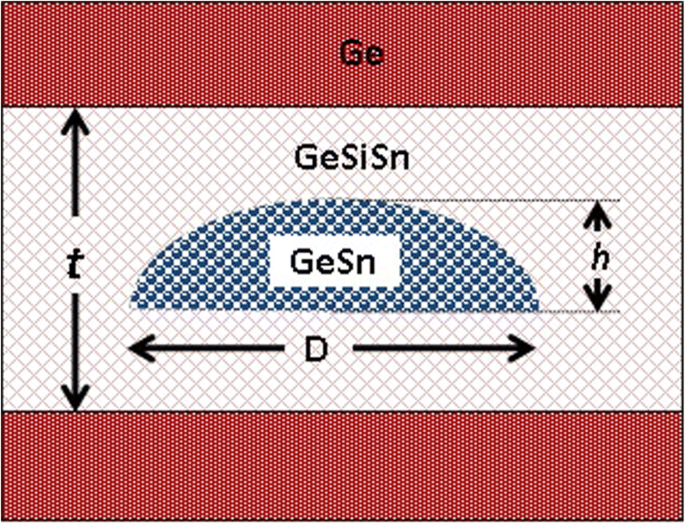
高度 (h) 的建模 GeSn QD 的示意图 ) 和直径 (D ) 在 Ge 基体中的 GeSiSn 应变降低层内

为了确保一致的 QD 设计以实现更好的发光器件操作，引入了合适的直接性参数，该参数考虑了 L 和 G 谷中最低 QD 受限能级位置之间的能量间距 [18]。该参数用 GSL-GSΓ 表示，应高于室温热能以避免载流子因热激活而损失，其中 GSL(GSΓ) 表示 L 谷（Γ 谷）中的电子基态能级，与价带最大值。 GSL-GSΓ 的评估示意性地显示在图 3 的插图中。

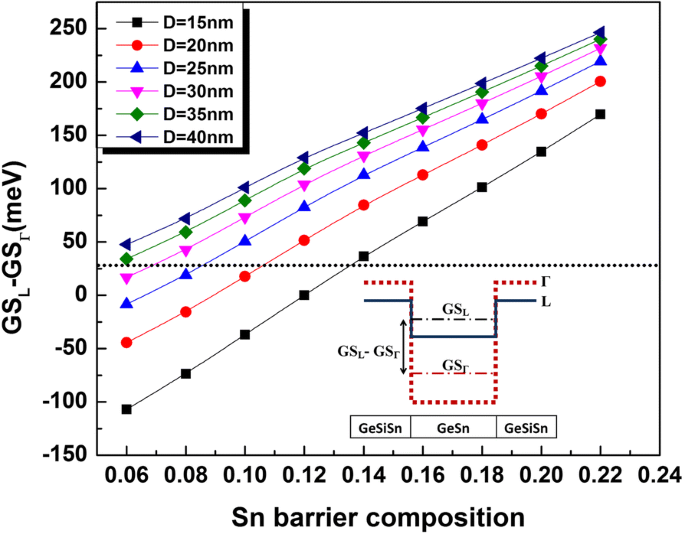
作为 Ge0.72Sn0.28 QD 尺寸和 Ge0.65-x 的 Sn 成分的函数的直接性参数 (GSL-GSΓ) 变化 Si0.35Sn x 周围层。虚线表示室温下的热能。插图表示直接性参数的示意性定义

计算不同直径的 Γ 和 L 谷中的 GeSn QD 电子能级作为 GeSiSn 中 Sn 成分的函数可以获得相应的直接性参数 (GSL-GSΓ)。结果绘制在图 3 中。对于给定的 x b ，GSL-GSΓ 的值主要由 QD 大小决定。因此，具有明显较高受限能态的较小点通过应变减小需要较低的带隙能量以满足直接性标准。如图 3 所示，较大的点 (D> 25 nm) 满足 GSL-GSΓ> 26 meV for x b 高于 8%。然而，发现对于 x 的较高值可以确保来自小尺寸 QD 的有效直接带隙 b (x b D ≥ 14% =15 纳米）。

在这项工作中采用的参数内，特别是二元材料的弯曲参数，GeSiSn 材料中 Sn 含量的增加减少了 QD 周围的污点，也减少了周围材料的带隙。事实上，如图 1b 所示，x 的增加 b 从 6% 到 22% 将 Γ 谷的导带不连续性从 0.72 eV 降低到 0.23 eV。事实上，如图 4 所示，其中量子点中基态电子的平方波函数 \( {\left|\uppsi \left(\overrightarrow{r}\right)\right|}^2 \)对于 6% 和 22% 的 Sn 势垒成分，xy 平面中显示了 35 nm 的直径，发现电子完全位于 QD 内部，而与势垒成分无关（导带的不连续性）。强限制电子表明所研究的QD作为Si衬底上发光体的活性介质具有更高的可靠性。

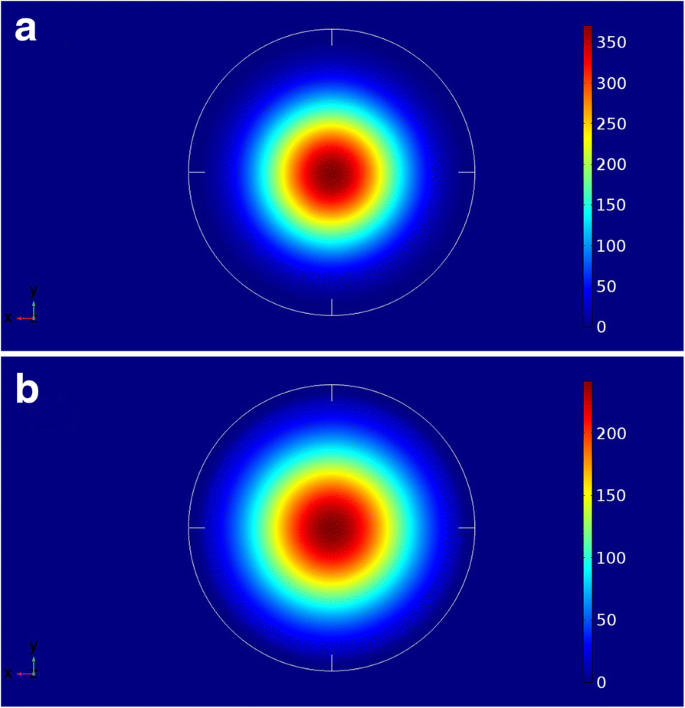
a 35 nm 直径 Ge0.72Sn0.28 QD 的平方电子基态波函数 Xb =6% 和 b Xb =22%

通过限制给定 x 的 QD 大小 b 对于那些产生有效的直接带隙发射，我们评估了 QD 基态带间发射波长。结果如图 5 所示，其中发射波长相对于 x b 对于不同的 QD 尺寸。值得注意的是，本工作中考虑的最大 QD 尺寸 (D =40 nm) 显示电子基态和第一激发态（低于 26 meV）之间的能量分离很小，因此在本研究中被忽略。尽管如此，评估的发射波长作为 x 的函数 b 已在图 5 中用虚线保留。

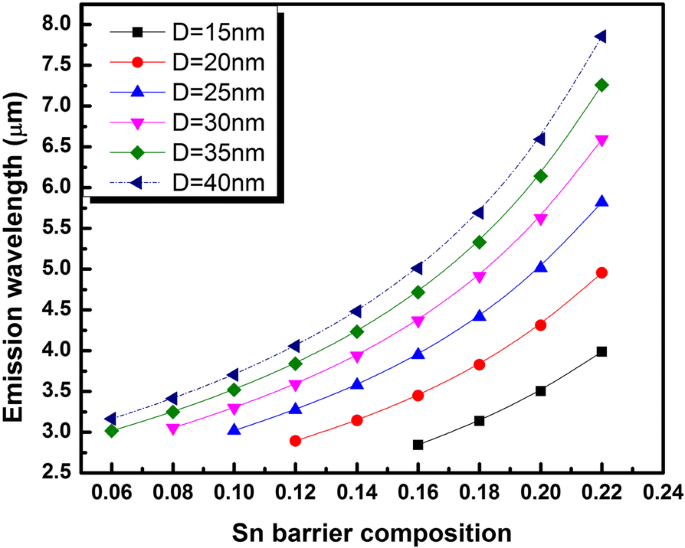
来自直接带隙 Ge0.72Sn0.28 QD 的室温基态发射波长与 Ge0.65-xb 的尺寸和 Sn 成分的函数关系 Si0.35Sn xb 周围层

拟议的 QD 设计预计涵盖的波长范围为 3 至 7 微米。屈服范围对于气体传感应用极为重要。这种结构的实验实施可以提供机会，首次使用与现有微电子技术完全兼容的材料覆盖整个中红外范围，为基于 CMOS 兼容 QD 的中红外光电子学的新视角铺平道路。

结论

已经研究了 Ge 基体上 GeSiSn 应变工程层中的 GeSn QD 作为 QD 尺寸和与周围材料的晶格失配的函数。发现通过改变 GeSiSn 势垒材料的 Sn 成分来降低 GeSn QD 周围的应变，可以将直接带隙 I 型发射波长从 3 μm 提高到 7 μm。所设计的结构为完全兼容Si技术的中红外光发射器开辟了新的前景。

缩写

CMOS：

互补金属氧化物半导体

GSL：

L谷基态电子能级

GSΓ :

Γ谷基态电子能级

QD：

量子点