相关量子点侧耦合到马约拉那束缚态的热电效应

介绍

零能马约拉纳束缚态 (MBS) 的制备和检测在现代凝聚态物理中尤为重要。从根本上说，MBS 是马约拉纳费米子的固态对应物，并且与非阿贝尔统计相关联，可以使拓扑保护的量子信息在没有退相干的量子计算中具有潜在应用[1-3]。除此之外，MBSs 在高效电子器件的设计中也很有前景，例如自旋电子学 [4]。分离良好的 MBS 可以在各种系统中制备，其中最重要的方案包括非中心对称超导体 [5]、与超导体耦合的三维或二维拓扑绝缘体 [6]、拓扑超导体中的静电缺陷 [7]、 p 波超导体 [8]、半导体 [9] 或铁磁 [10] 纳米线与传统的 s 波超导体具有很强的自旋轨道相互作用，以及约瑟夫森结 [11]。

至于 MBS 的检测，它也是相当具有挑战性的，因为马约拉纳费米子是它们自己的反粒子，并且由于其固有的粒子 - 空穴对称性而具有电荷中性。已经进行了各种实验以通过 4π 等现象来验证 MBS 的存在 拓扑超导体之间结中的周期性约瑟夫森电流相位 [12]，由拓扑超导体和拓扑量子异常霍尔绝缘体组成的混合结构中矫顽场的半整数电导平台 [13]，使用 Rashba 纳米线耦合到体 s 的隧道光谱波超导体 [14]，以及导线边缘微分电导的零偏置 [14, 15]。然而，除了 MBS 之外，这些现象还有其他可能的物理起源，并且已经提出了替代方案。其中之一是 MBS 与其他纳米级结构的杂交，例如零维量子点 (QD)，其中能级、电子-电子库仑相互作用、粒子数和与外部环境的耦合强度都可以很好地控制。 16, 17]。在低温下，当 QD 的能级与引线中的费米能量对齐时，半最大电导理论上被预测为形成一对 MBS [18] 的明确证据。通过调整 QD 能级 [19] 并在实验中成功地观察到 QD 耦合到 InAs-Al 纳米线 [20]，该结果完全不变。最近，还从理论上提出了基于 QD 结构的光学方案，以借助光泵浦探测技术来检测 MBS。 [21, 22] 在基于环形或 T 形 QD 的系统中，量子干涉现象受到 MBS [23-25] 的极大影响，然后可用于检测方案，例如，范诺效应[26-28]。

最近，也有一些关于通过热电效应检测 MBS 的工作，其重点是电能和热能之间的转换。由于细观器件和纳米结构的生长和制造的快速进展，其中热电性能得到明显改善，这一古老的研究课题获得了新的关注 [29, 30]。最近报道了基于 QD 的高效能量收集器，这些 QD 定义在 GaAs/AlGaAs 界面二维电子气上 [31, 32]。它们中热电效应的增强可归因于边界散射导致的热导率显着降低以及这些低维系统中独特的电传输特性的优化 [30-32]。热电势（塞贝克系数）是热电效应的中心量。它是对施加在具有自由电子载流子的固体材料中的温度梯度做出响应的开路电压强度。侯等人。理论上预测 QD 和拥有 Majorana 边缘态的超导体之间的热电势满足 Mott 公式，并且一般不会通过使用 Landauer-Büttiker 形式主义而消失 [33]。基于这一特性，人们可以通过测量微分电导和热电势来推断马约拉纳边缘态的温度。 Leijnse 从理论上证明了具有可调能级的 QD 与 MBS 之间的耦合打破了粒子-空穴对称性，而热电势的变化提供了一种证明马约拉纳态存在的新方法 [34]。这种设置中的热电特性还可用于检测超导体的温度并提取有关 MBS 耗散衰减的信息 [34]。在 QD 耦合到两个电极的结构中，López 等人。表明热电将通过改变 MBS 之间的直接杂交来改变其符号，这是 MBS 存在的一个很好的证据 [35]。随后在具有两个 [36] 或三个 [37] 电极的 QD 系统中也发现了热电势的符号变化。此外，还证明了散粒噪声和热电量之间的关系可以提供一种纯电的方式来检测电荷中性的 MBS [38, 39]。

在本文中，我们提出了一种由 MBS 和耦合到电极的 QD 组成的混合系统（见图 1）来研究热电的特性。在我们考虑的纳米系统中，点中的强库仑相互作用在以前的工作中被忽略 [18, 22-24, 34-39] 被考虑在内。此外，由于 MBS 的手性性质，我们认为 QD 自旋中只有一个自旋分量与 MBS 耦合[40]。我们发现通过改变点-MBSs 耦合强度、MBSs 之间的直接杂交和系统温度可以有效地逆转热电势的符号。由此产生的大 100% 自旋极化和纯自旋热电势，即闭路中相应的 100% 自旋极化和纯自旋电流，可用于自旋电子学。两个 MBS 与 QD 的耦合将进一步增强热电势的大小，但当只有一个 MBS 与点耦合时，不会改变基本结果。基于目前通过 QD 结合拓扑超导纳米线对 MBS 进行的先进量子传输测量，我们相信我们的提议可以在未来进行实验测试。此外，我们在这项工作中的提议和发现可能为检测 QD 中 MBS 的形成提供一种极好的方法。

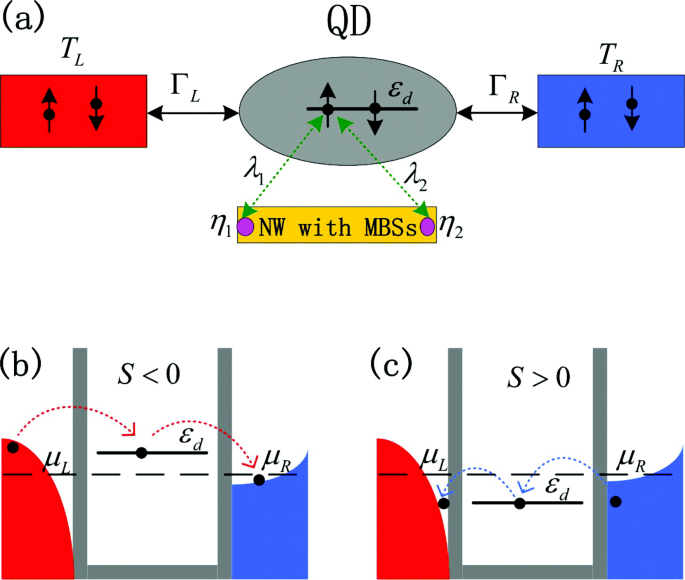
模型示意图（在线颜色）。 一 具有栅极可调能级ε的量子点组成的模拟结构示意图 d 它可以被自旋向上或自旋向下的电子占据。 QD 以耦合强度 Γ 连接到保持在不同温度下的左右引线 L /R . MBS η 由于强度为 λ 的马约拉纳费米子的手性性质，1/2 形成在半导体纳米线的末端并与 QD 中的自旋电子耦合 1 和 λ 2、分别。 MBSs-QD耦合会改变自旋电子的能态，进而改变热电势S的强度和符号 会受到影响。在本模型中，我们假设左引线的温度 T L 高于右边的T R ，然后，在左引线中比在右引线中的化学势之上（之下）有更多的电子（空态）被激发。 b , c 在没有 MBSs-QD 耦合的情况下，电子隧穿过程和产生的热电势。在b , QD 能级 ε d 高于导联μ的化学势 L /R =μ ，然后，来自占据态 ε 的电子 d>μ 在左侧较热的引线将隧道通过点状态 ε d 到右侧较冷引线的空状态，导致负热电介质 S <0。在c , ε d <μ ，然后，热电势的符号相应反转

模型和方法

耦合到 MBS 和左右法向金属电极的 QD 的有效哈密顿量采用以下形式[34, 35]：

其中 \(c_{k\beta \sigma }^{\dag } (c_{k\beta \sigma })\) 创建（湮灭）一个动量为 k 的电子 , 能量 ε k β （对于普通金属电极忽略其对自旋的依赖性），自旋σ =↑ ,↓ 在电极β =L ,R .对于 QD，\(d_{\sigma }^{\dag } (d_{\sigma })\) 是具有栅极电压可调能级 ε 的电子的创建（湮灭）算子 d , 自旋 σ , 和内点库仑相互作用 U . QD 和引线之间的耦合强度由 V 描述 k β .最后一项H 方程式中的 MBS。 (1) 代表位于半导体纳米线两端的零能量 MBS 及其与 QD 的耦合 [18]：

其中δ M 是两个 MBS 之间的重叠幅度，算子同时满足 \(\eta _{j}=\eta _{j}^{\dag } (j=1,2)\) 和 {η 我 ,η j }=δ 我 ,j . MBSs与自旋之间的跳跃幅度↑ 量子点中的电子由 λ 计算 j .写η很有帮助 j 根据常规费米子算符 f 如 [18] \(\eta _{1}=(f^{\dag }+f)/\sqrt {2}\) 和 \(\eta _{2}=i(f^{\dag }- f)/\sqrt {2}\)，然后，H MBSs 重写为：

我们考虑处于线性响应状态的系统，即在无限小的偏置电压 Δ 下 V 和温差Δ T 在左右引线之间，得到每个自旋分量的电流和热电流为：

其中 e 是电子电荷和 T 系统平衡温度，和

其中 \(\hbar \) 是约化的普朗克常数。我们设置引线的化学势μ =0 作为能量零点。费米分布函数由 f 给出 (ε ,μ )=1/{1+exp[(ε -μ )/k B T ]} 与 k B 是玻尔兹曼常数。透射系数T σ (ε ) 借助滞后格林函数计算为：

其中 \(\Gamma _{L(R)}=2\pi \sum _{k}|V_{kL(R)}|^{2}\delta [\varepsilon -\varepsilon _{kL(R)} ]\) 是线宽函数。我们应用标准运动方程技术来获得格林函数。高阶格林函数通过参考文献中的方案 2 截断。 [39]，即忽略相反自旋电子的同时隧穿。经过一些简单的计算，自旋延迟格林函数由下式给出：

结果和讨论

在下文中，我们假设 QD 和电极之间对称耦合，并设置 Γ =2Γ L =2Γ R =1 作为能量单位。点内库仑相互作用固定为 U =10Γ .我们首先研究了QD仅与具有不同杂交强度λ的MBS-1偶联的情况 图 2 中的 1 通过设置 λ 2=0。对于 λ 1=0，图2a中每个自旋分量的电导分别在ε处形成两个峰 d =-μ 和-μ -U .请注意，现在 QD 没有由 MBS 引起的自旋极化，并且两个自旋分量的电导彼此相等 (G ↑ =G ↓ ）， 因此。打开 MBS 和 QD 之间的杂交 (λ 1≠0)，G的大小 ↑ 被单调抑制，如图 2a 所示，这与之前的结果一致 [18, 34, 35]。 G的价值 ↓ ，然而，即使是职业数n也几乎没有变化 ↓ 由 λ 改变 1 由于存在点内库仑相互作用（图中未显示）。同时，G中峰的位置和宽度 ↑ λ 的值略有修改 由于 dot-Majorana 耦合的水平重整化 [18, 34, 35]。总电导G的配置 =G ↑ +G ↓ 在图 2c 中类似于 G ↑ .

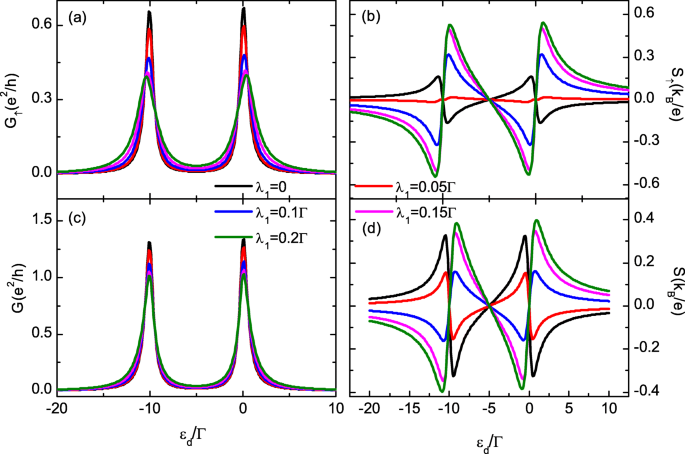
不同点-Majorana 耦合强度的自旋相关电导和热电势（在线颜色）。 a 中的自旋和总电导 , c 和 b 中的热电 , d 诗句点级。点-Majorana 耦合强度λ几乎没有改变自旋电导和热电势 1，它们与a中的黑色实线重叠 和 c ， 分别。其他参数是温度T =0.025Γ ,Δ M =0,U =10Γ , 和 λ 2=0

热电S ↑ 图 2b 中显示了典型的锯齿配置，并且在 ε 处分别具有三个零点 d =μ ,-U /2 和 μ -U [41, 42]。它在两个共振态 (ε d =μ ,μ -U ) 并在 ε 时改变符号 d 通过每个零点。在没有点-MBSs 杂交的情况下 (λ 1=0) 如图 2b 中黑色实线所示，S ↑ 当 ε 时为正（负） d 低于（高于）零点，因为主要载流子是电子（空穴）。随着λ的增加 1、自旋热电S ↓ 不变且 S 的绝对值 ↑ 先抑制后增强。对于足够大的λ 1、S ↑ 如图 2b 所示改变其符号。随着λ的进一步增加 1、S的绝对值 ↑ 超过S ↓ 和总热电势 S =S ↑ +S ↓ 也会改变它的符号。先前在无旋转模型中也发现了这种现象[35-37]。事实上，在没有 MBS 的基于 QD 的设备中，热电势的符号变化归因于几个原因，例如系统平衡温度 [29]、电极的磁动量 [43]、库仑相互作用 [43、44]、耦合量子点之间的强度、施加的磁场、量子干涉效应或穿透多点的磁通量 [45, 46]。上述机制与目前的情况有很大不同，通过改变QD和MBSs之间的杂交来改变热电势的符号有助于检测MBSs[35-37]。

图 3a、b 显示了总电导G 和 themopower S 随网点等级ε而变化 d 对于不同的温度值 T . G 的峰值 如图 3a 所示，通过升高温度首先增强然后抑制。然而，图 3b 中热电势的大小主要通过升高温度而增强，因为有更多的电子（空穴）在化学势之上（之下）被激发。此外，S 对于 T 的情况改变其符号 =0.1 和 0.2，如图 3b 中粉红色和绿色线所示，这类似于没有 MBS 的 QD 结构中的热电效应情况。对于 T =0.2Γ , S 的峰值 可以达到 2k B /e , 比 T 大一个数量级 =0.001。事实上，我们已经检查过，通过提高温度可以进一步增强热电势的大小。然而，在本文中，我们关注 S 的符号变化 在相对较低的温度下，这通常是实验中形成的 MBS 的情况。图 3c、d 显示了在固定 T 下纳米线两端的两个 MBS 直接杂交的不同值的电导和热电势 =0.025Γ .图3c中电导的峰值随着δ的增加而单调增强 M ，这与 López 等人发现的结果一致。 [35]。图 3d 中的热电势改变其符号为 0.03Γ <δ M <0.05Γ , 大于温度 T =0.025Γ .在参考。 [32]，他们发现热电势在大约 δ 处改变其符号 M ≈k B T 在无旋转模型中。在本文中，S的符号变化 发生在相对较大的δ M 因为 MBS 只与一个自旋方向的电子耦合。此外，还可以通过增加δ来提高热电的峰值 M .

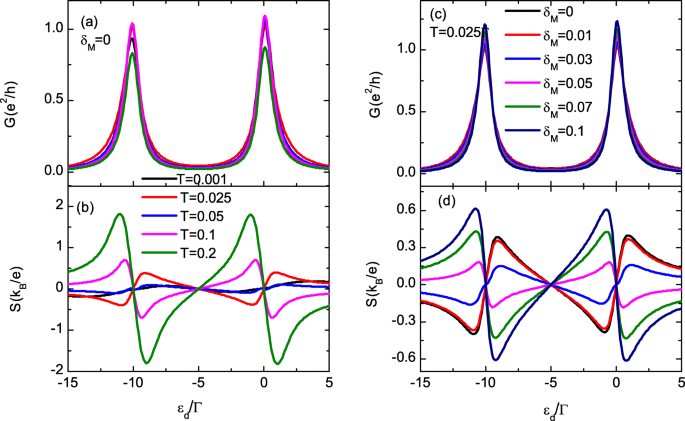
电导和热电势（在线颜色）。总电导G的计数器图 和热电S 作为 ε 的函数 d 和Δ M 在 a , b , 温度 T 在 c , d ， 分别。 λ的值 1 固定为 0.2Γ . a 中的温度 , c 是 0.025Γ , 并在 c 中 , d Δ M =0。其他参数同图2

我们将自旋分辨的热电势分别显示为 λ 的函数 1 和 δ M 在图 4. 自旋热电 S ↑ 图4a中随着λ的增加，先增加，达到最大值后减小 1.在足够大的λ 1，它保持在一个稳定的值。自旋热电S的价值 ↓ λ 不变 1 如预期。 S 的行为 ↑ 和 S ↓ 带来两个有趣的结果：一个是 S 时的 100% 自旋极化热电势 ↑ =0 但S ↓ 具有可用于过滤电子自旋的有限值；另一个是有限纯自旋热电S s =S ↑ -S ↓ 零电荷热电S c =S ↑ +S ↓ =0 发生在 S ↑ =-S ↓ 如图 4b 中的点所示。在闭合电路中，100% 自旋极化和纯自旋热电势分别是相应的电流，在自旋电子器件中是虚拟的。在图 4b、d 中发现了类似的结果，其中 S ↑ 通过改变 δ 进行符号变化 M , 而 S ↓ 保持不变。我们强调，目前的 100% 自旋极化和纯自旋热电势是在 QD 中没有磁场或磁性材料的情况下出现的。

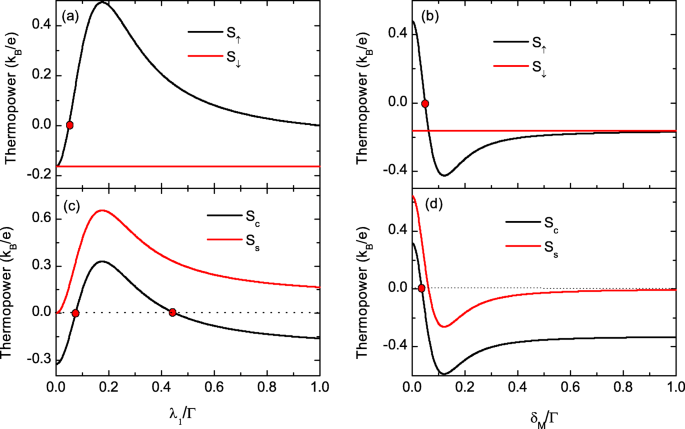
热电势随 dot-Majorana 耦合强度和直接重叠而变化。作为 λ 函数的热电势 a 中的 1 , b Δ M =0 和 Δ M 在 c , d 与 λ 1=0.2Γ ， 分别。其他参数同图2

在图 5 中，我们研究了当纳米线和点彼此足够接近并且 δ 时，纳米线两端的两个 MBS 都耦合到 QD 的情况 M =0。图 5a 显示总电导 G 在 λ 存在的情况下保持双峰构型 2. 增加λ会抑制峰高 2.S的线型 λ 的值也没有改变 2如图5b所示。 S 的峰值 将显着增强，因为热功率与电导成反比。对于 λ 2∼0.2Γ , 热电势的大小可以达到 2 k B /e .此外，我们发现 S 不会通过调整 λ 的值来改变其符号 2. 图 6 显示了作为 ε 函数的总热电势 d MBSs之间的不同直接杂交值δ M 通过固定 λ 1=λ 2=0.2Γ .这表明通过调整δ可以有效地改变幅度和符号 M ，这类似于只有一个 MBS 耦合到 QD 的情况。最后，我们简要讨论了本设备的实验实现。承载 MBS 的纳米线可以用通过分子束外延生长的 InAs 制造，并具有几纳米的外延 Al 层 [47]。实验证明，通过沿线轴施加超过 2 T 的临界磁场 [20]，可以在这种纳米线 [47, 48] 上感应出硬超导间隙。由于铝壳边缘的状态梯度密度，在导线末端的裸 InAs 段中形成 QD [20, 47, 48]。

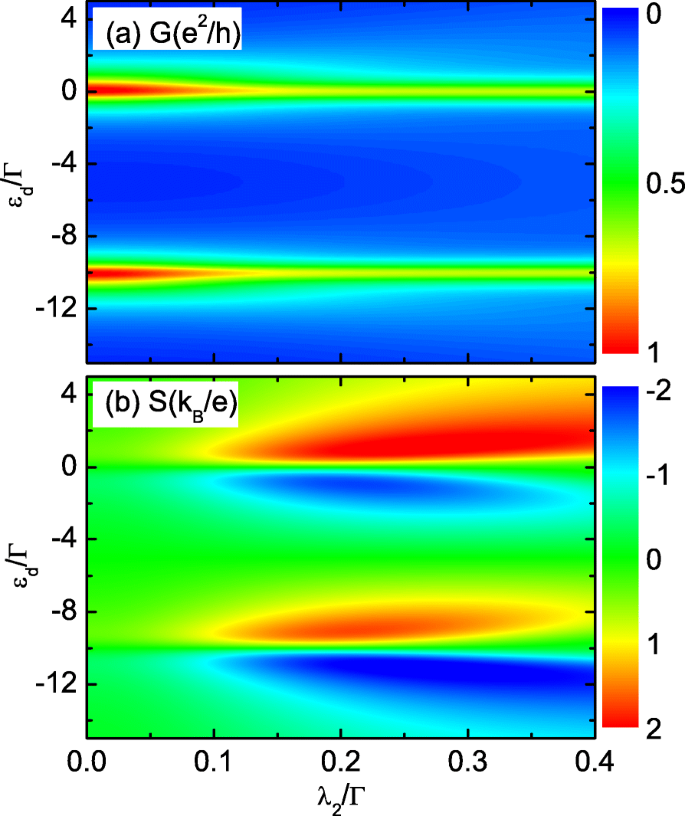
其他 dot-Majorana 耦合对热电势的影响（在线颜色）。 λ 的影响 2 关于总电导 (a ) 和热电 (b ) 与 λ 1=0.2Γ ,δ M =0。其他参数同图2

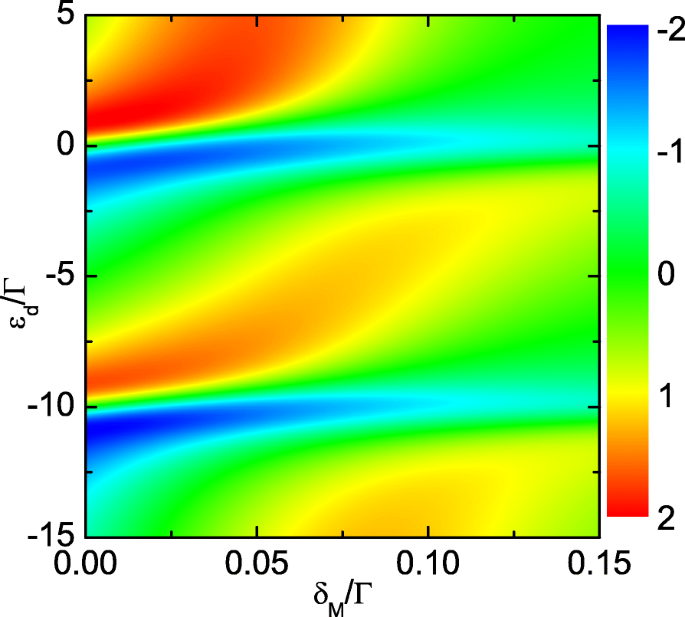
热电势的计数器图（在线颜色）。作为 ε 函数的热电势计数器图 d 和 λ 2 对于 λ 1=0.2Γ .其他参数同图2

结论

总之，我们研究了通过库仑相互作用连接到左右普通金属电极的量子点中的电导和热电特性。该点还与形成在半导体纳米线中的 MBS 耦合。我们发现 MBS 会影响它只耦合到的自旋分量的电导率和热功率，尽管自旋向上和自旋向下的电子通过库仑排斥相互作用。可以通过调整点-MBSs 杂交强度、MBSs 之间的方向杂交和系统温度来改变热电势的符号。在非磁性 QD 结构中可以获得 100% 自旋极化或纯自旋功率的大值。点与两个 MBS 之间的耦合只能改变热电势的大小，而不能改变其符号。我们的研究结果可能有助于通过热电技术检测MBSs的存在。

数据和材料的可用性

本文包含支持本文结论的数据集。

缩写

QD：

量子点

MBS：

马约拉纳束缚态