SPICE 是一种旨在模拟模拟电子电路的计算机程序。它的初衷是为了开发集成电路，因此得名：S 模拟P I 的程序 集成C ircuit E 强调。 SPICE 的起源可以追溯到另一​​个名为 CANCER 的电路仿真程序。由加州大学的 Ronald Rohrer 教授开发。伯克利和他的一些学生在 1960 年代后期，癌症在 1970 年代初期继续得到改善。当 Rohrer 离开伯克利时，CANCER 被重写并重新命名为 SPICE，于 1972 年 5 月作为第 1 版发布到公共领域。 SPICE 的第 2 版于 1975 年发布（版本 2g6——本书中使用的版本——是1975 年版本的小修

“使用 Electronics Workbench，您可以创建与您在纸上熟悉的电路原理图完全相同的电路图——此外，您还可以翻转电源开关，使原理图表现得像真正的电路。使用其他电子模拟器时，您可能需要将 SPICE 节点列表作为文本文件输入——这是一种电路的抽象表示，超出了高级电子工程师的能力范围。” —（Electronics Workbench 用户指南—第 4 版，第 7 页） 这个介绍来自一个名为Electronics Workbench的电路仿真程序的操作手册 .使用图形界面，它允许用户绘制电路原理图，然后让计算机分析该电路，以图形形式显示结果。它是一种非常有价值的分析工具，但也有其

与解是数字的正规方程相反，微分方程是解实际上是一个函数的方程，并且该未知函数的至少一个导数是方程的一部分。 与寻找函数的反导数一样，我们经常会得到一个包含不止一种可能性的解决方案（考虑在反导数中常见的常数“c”的许多可能值）。回答任何微分方程的函数集称为该微分方程的“通解”。该集合中的任何一个函数都称为该微分方程的“特定解”。微分方程中用于微分和积分的参考变量称为“自变量”。

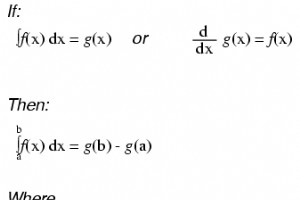
相关工作表： 电路微积分练习题

恒定法则 求和法则 差异法则

的幂函数的反导数 注意：这是 e 的一个非常独特和有用的属性。与导数的情况一样，这种函数的反导数是同一个函数。在反导数的情况下，常数项“c”也被添加到末尾。

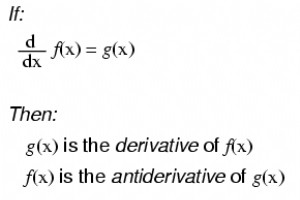
请注意这里重要的一点：取 f(x) 的导数可能精确地得到 g(x)，但取 g(x) 的反导数不一定会得到原始形式的 f(x)。示例： 请注意，常数 c 是未知的！原始函数 f(x) 可能是 3x2 + 5, 3x2 + 10, 3x2 + 任何东西 ，并且 f(x) 的导数仍然是 6x。因此，确定函数的反导数比确定函数的导数更不确定。 相关工作表： 电路微积分练习题

常量规则 求和规则 差异法则 产品规则 商数法则 权力规则 其他函数的作用 相关工作表： 电路微积分练习题

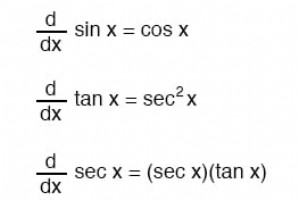
相关工作表： 电路微积分练习题

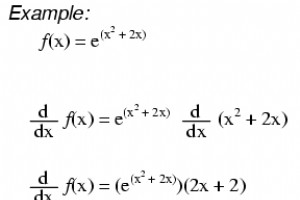
的幂函数的导数 e 的导数示例 比例常数 当我们说一种关系或现象是“指数的”时，我们是在暗示某些数量——电流、利润、人口——随着数量的增加而增加得更快。换句话说，相对于给定变量的变化率与该变量的值成正比。这意味着指数函数的导数等于原始指数函数乘以一个常数 (k ) 建立相称性。 $$\frac{\text{d}}{\text{d}x}a^x=ka^x$$ 比例常数等于指数底的自然对数： $$\frac{\text{d}}{\text{d}x}a^x=\ln(a)\times a^x$$ 因此，如果底的自然对数等于 1，则函数的导数将等于原始函数。这正是 e 的幂函数发生的情况

相关工作表： 电路微积分练习题

（“c”是一个常数） 相关工作表： 电路微积分工作表

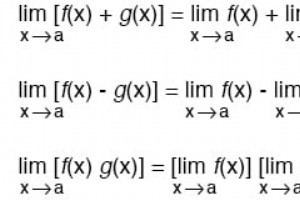
相关工作表： 电路微积分工作表

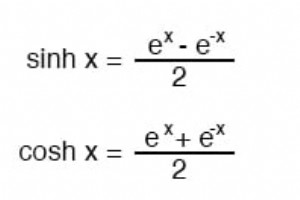
注意：所有角度 (x) 必须以弧度为单位表示 对于这些双曲函数。一个圆有 2π 弧度 (360o ).

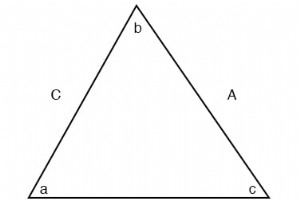
正弦定律（对于任何三角形） 余弦定律（对于任何三角形）

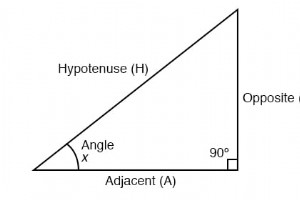
直角三角形 定义为一个角正好等于 90o （直角 ). 三角恒等式 H 是 斜边 ，总是对着直角。相对于角度 x，O 是 Opposite A 是 Adjacent . “arcsin”、“arccos”、“arctan”等“arc”函数是普通三角函数的补充。 这些函数为比率输入返回一个角度。例如，如果 45o 的切线 等于1，那么1的“反正切”（arctan）就是45o . 如果边长已知，“弧”函数对于在直角三角形中求角很有用。 勾股定理 相关工作表： 交流电路三角学工作表

什么是联立方程和方程组？ 项联立方程 和方程组 指两个或多个未知变量通过相等数量的方程相互关联的条件。 示例： 对于这组方程，x 只有一个值组合 和 y 这将满足两者。 任何一个方程，单独考虑，都具有无限的有效 (x,y) 解决方案，但一起 只有一个。绘制在图表上，这种情况变得明显： 每条线实际上是一个连续的点，代表可能的 x 和 y 每个方程的解对。 每个方程分别有无数个有序对 (x ,y ) 解决方案。两个线性函数只有一点x + y =24 和 2x - y =-6 相交（其中许多独立解中的一个恰好适用于两个方程），这就是 x 等于 6 和 y 的值 等于

因子的定义 用符号 “!” 表示 整数后；该整数与所有下降到 1 的整数的乘积。阶乘示例： 5！ =5 x 4 x 3 x 2 x 1 5！ =120 奇怪的因子 0！ =1 1！ =1 相关工作表： 相量数学工作表