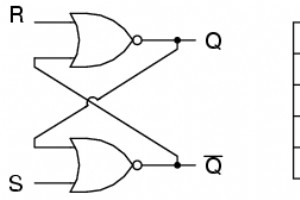
双稳态多谐振荡器有两个 稳定状态，如前缀 bi 所示 以其名义。通常，一种状态称为 set 另一个是reset .因此，最简单的双稳态设备被称为 set-reset ，或 S-R，锁存器。要创建 S-R 锁存器，我们可以连接两个 NOR 门，使一个的输出反馈到另一个的输入，反之亦然，如下所示： Q 和非 Q 输出应该处于相反的状态。我说“应该”是因为让 S 和 R 输入都等于 1 会导致 Q 和非 Q 都为 0。因此，S 和 R 都等于 1 被称为 无效 或非法 S-R 多谐振荡器的状态。 否则，使 S=1 和 R=0 “设置”多谐振荡器，使 Q=1 而 not-Q=0。相反，

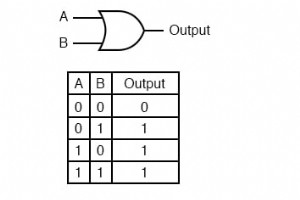
对于简单的门电路和组合逻辑电路，任何给定的输入状态都有一个明确的输出状态。以 OR 门的真值表为例： 对于输入状态的四种可能组合（0-0、0-1、1-0 和 1-1）中的每一种，都有一个明确的、明确的输出状态。无论我们是处理多个级联门还是单个门，输出状态都由电路中门的真值表决定，仅此而已。 然而，如果我们改变这个门电路以将信号从输出反馈到输入之一，奇怪的事情就会开始发生： 我们知道如果 A 是 1，输出 must 也为 1。这就是或门的性质：任何“高”(1) 输入都会强制输出“高”(1)。但是，如果 A 为“低”（0），则我们无法保证真值表中输出的逻辑电平或状态。

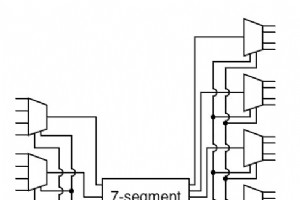
作为一起使用多个电路的示例，我们将制作一个具有 16 个输入的设备，代表一个四位数字，到一个四位 7 段显示器，但只使用一个二进制转 7 段编码器. 首先，我们电路的整体架构提供了与我们提供的描述相似的内容。 遵循此电路，您可以确认它与上面给出的描述相符。有 16 个主要输入和另外两个用于选择将显示哪个数字的输入。 有 28 个输出来控制四位 7 段显示器。一次只对四个主要输入进行编码。不过，您可能已经注意到一个潜在的问题。 选择其中一个数字时，其他三位数显示的是什么？查看解复用器的电路，注意没有被 A 输入选择的任何线路都为零。 所以其他三个数字是空白的。我们没有问

多路复用器，缩写为 mux，是一种具有多个输入和一个输出的设备。 多路复用器的原理图符号为 2 比 1 多路复用器的真值表是 I1I0AD00000010010001111001101011011111 使用1对2解码器作为电路的一部分，我们可以很容易地表达这个电路。 复用器也可以使用与解复用器相同的命名约定进行扩展。一个4对1多路复用器电路是 这是多路复用器的正式定义。非正式地，有很多混乱。解复用器和复用器都有相似的名称、缩写、原理图符号和电路，因此很容易混淆。术语多路复用器和缩写 mux 通常也用于表示多路分解器，或多路复用器和

解复用器，有时缩写为 dmux，是一种具有一个输入和多个输出的电路。当电路打算向许多设备之一发送信号时使用它。这个描述听起来类似于对解码器的描述，但解码器用于在许多设备中进行选择，而解复用器用于在许多设备之间发送信号。 解复用器的使用频率很高，它有自己的原理图符号（下图） 1对2解复用器的真值表是： IAD0D10000010010101101 使用我们的 1-to-2 解码器作为电路的一部分，我们可以很容易地将这个电路表示为： 该电路可以扩展为两种不同的方式。您可以增加传输的信号数量，也可以增加通过的输入数量。要增加通过的输入数量，只需要

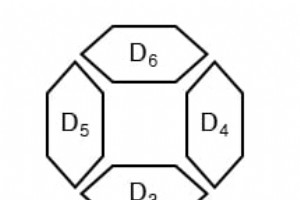
什么是编码器？ 编码器是将一组信号转换为代码的电路。让我们通过反转 1-to-2 解码器真值表开始制作 2-to-1 线编码器真值表。 D1D0A010101 这个真值表有点短。一个完整的真值表是： D1D0A00 01010111 我们需要回答的一个问题是如何处理其他输入？我们忽略它们吗？我们是否让它们生成额外的错误输出？在许多电路中，这个问题是通过添加时序逻辑来解决的，以便不仅知道哪个输入是活动的，而且知道输入变为活动的顺序。 编码器设计应用 组合编码器设计的一个更有用的应用是二进制到 7 段编码器。七段是根据： 我们的真值表是： I3I2I1I0D

解码器是将代码转换为一组信号的电路。之所以称为解码器，是因为它与编码相反，但我们将从编码器和解码器的研究开始，因为它们更易于设计。 解码器的类型 线路解码器 一种常见的解码器是行解码器，它接受一个 n 位二进制数并将其解码为 2n 数据线。最简单的是1对2线解码器。真值表是： AD1D0001110 A是地址，D是数据线。 D0 不是 A，D1 是 A。电路如下图所示。 2 到 4 行编码器 仅稍微复杂一点的是 2 到 4 行解码器。真值表是： A1A0D3D2D1D0000001010010100100111000 开发成如下图所示的电路。

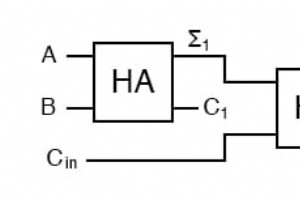
半加器非常有用，直到您想要添加一个以上的二进制数字量。开发两个二进制数字加法器的缓慢方法是制作一个真值表并减少它。然后当你决定做一个三位二进制加法器时，再做一次。然后当你决定做一个四位加法器时，再做一次。那么当......电路会很快，但开发时间会很慢。 查看两个二进制数字和显示我们需要将加法扩展到多个二进制数字。 11 11 11 --- 110 查看中间列使用了多少个输入。我们的加法器需要三个输入； a、b 和前一个和的进位，我们可以使用我们的两输入加法器构建一个三输入加法器。 Σ 是容易的部分。普通算术告诉我们，如果 Σ =a + b + Cin 和 Σ1 =a + b，那么 Σ

作为有用的组合逻辑的第一个示例，让我们构建一个可以将两个二进制数字相加的设备。我们可以快速计算出答案应该是什么： 0 + 0 =0 0 + 1 =1 1 + 0 =1 1 + 1 =102 所以我们需要两个输入（a 和 b）和两个输出。低阶输出将称为 Σ，因为它代表总和，而高阶输出将称为 Cout，因为它代表进位。真值表是： ABΣCout0000011010101101 简化布尔方程或制作一些卡诺图将产生如下所示的相同电路，但首先要查看结果。 Σ 列是我们熟悉的 XOR 门，而 Cout 列是 AND 门。这个设备被称为半加器，原因将在下一节中说明。 或在梯形

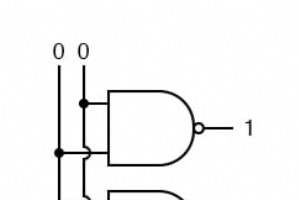
“组合”一词来自数学。在数学中，组合是一个无序集合，这是一种正式的方式，表示没有人关心项目的顺序。大多数游戏都是这样工作的，如果你一次掷一个骰子，得到一个 2，然后是一个 3，那就是就像您掷出 3 后掷出 2 一样。使用组合逻辑，无论输入更改的顺序如何，电路都会产生相同的输出。 有些电路取决于输入何时发生变化，这些电路称为时序逻辑。尽管您不会在章节标题中找到“顺序逻辑”一词，但接下来的几章将讨论顺序逻辑。 实际电路将混合使用组合逻辑和时序逻辑，时序逻辑确保一切都按顺序发生，而组合逻辑执行算术、逻辑或转换等功能。 您已经使用了组合电路。前面讨论的每个逻辑门都是一个组合逻辑函数。如果我们以不

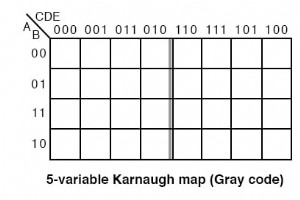
较大的卡诺图减少了较大的逻辑设计。多大才够大？这取决于输入的数量，扇入 , 到正在考虑的逻辑电路。大型可编程逻辑公司之一给出了答案。 从其客户设计库中提取的 Altera 自己的数据支持异质性的价值。通过检查逻辑锥，将它们映射到基于 LUT 的节点并按照每个节点上最好的输入数量对它们进行排序，Altera 发现扇入的分布在 2 到 6 个输入之间几乎是平坦的，并且有一个很好的峰值五点钟。 对于大多数设计，答案是不超过六个输入，对于平均逻辑设计不超过五个输入。五变量卡诺图如下。 五变量K-map 五变量 K-map 的旧版本，即格雷码图或反射图，如上所示。地图的顶部（以及 6 变量地

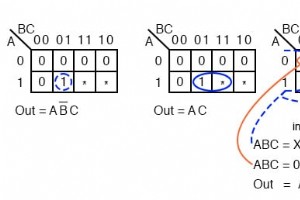
到目前为止，我们已经考虑了完全指定输入条件的逻辑归约问题。也就是说，一个 3 变量真值表或卡诺图有 2n =23 或 8 个条目，一个完整的表格或地图。 对于一些现实世界的问题，并不总是需要填写完整的真值表。我们可以选择不填写完整的表格。 例如，在处理编码为四位的 BCD（二进制编码的十进制）数字时，我们可能不关心任何高于 (0, 1, 2…9) BCD 范围的代码。十六进制数（Ah、Bh、Ch、Eh、Fh）的4位二进制码不是有效的BCD码。 因此，如果我们不关心，我们不必在真值表或 K-map 的末尾填写这些代码。 我们通常不会关心填写这些代码，因为只要我们只处理 BCD 编码的数字

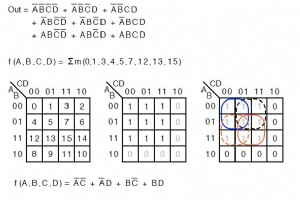
作为参考，本节介绍了一些文本中用于描述分配给卡诺图的 minterms 和 maxterms 的术语。否则，这里没有新材料。 Minterms 的术语 Σ (sigma) 表示总和，小写“m”表示最小项。 Σm 表示最小项的总和。重新审视以下示例以说明我们的观点。我们列出了最小项，而不是对未简化逻辑的布尔方程描述。 f(A,B,C,D) =Σ m(1, 2, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15) 或者 f(A,B,C,D) =Σ(m1,m2,m3,m4,m5,m7,m8,m9,m11,m12,m13,m15) 数字表示卡诺图中的单元格位置或地址，如

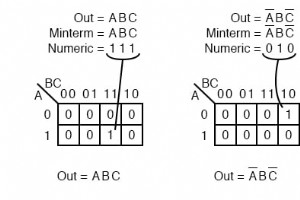
到目前为止，我们一直在寻找逻辑归约问题的总和 (SOP) 解决方案。对于这些 SOP 解决方案中的每一个，还有一个总和解决方案 (POS)，这可能更有用，具体取决于应用程序。 在使用乘积解决方案之前，我们需要介绍一些新术语。以下用于映射产品术语的过程对本章来说并不陌生。 我们只是想建立一个minterms的正式程序，以便与maxterms的新程序进行比较。 小项 minterm 是一个布尔表达式，结果为 1 对于单个单元格的输出，0 s 表示卡诺图或真值表中的所有其他单元格。如果一个 minterm 有一个 1 其余单元格为 0 s，它似乎覆盖了 1 的最小区域 s. 左

知道如何生成格雷码应该能让我们构建更大的地图。实际上，我们需要做的就是在 3 变量映射的顶部查看从左到右的序列，并将其复制到 4 变量映射的左侧。见下文。 减少 4 个可变 K 映射 以下四个变量卡诺图说明了对布尔代数来说过于繁琐的布尔表达式的减少。可以使用布尔代数进行归约。 但是，卡诺图更快更容易，尤其是在需要进行很多逻辑归约的情况下。 上面的布尔表达式有七个乘积项。它们在上面的 K 图中从上到下和从左到右映射。例如，第一个 P-term ABCD 是第一行，第三个单元格，对应地图位置A=0, B=0, C=1, D=1 . 其他乘积项的放置方式类似。将可能的

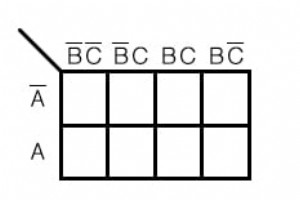
到目前为止，我们已经完成的逻辑简化示例可以用布尔代数执行。现实世界的逻辑简化问题需要更大的卡诺图，以便我们可以做认真的工作。 我们将在本节中使用一些人为的示例，将大多数现实世界的应用程序留给组合逻辑章节。人为设计是指说明技术的示例。 这种方法将开发我们需要的工具，以过渡到组合逻辑章节中更复杂的应用程序。 卡诺图和格雷码序列 我们展示了我们之前开发的卡诺图。我们将使用右侧的表格。 请注意地图顶部的数字序列。它不是 00, 01, 10, 11 的二进制序列 .它是 00, 01, 11 10 ，即格雷码序列。与二进制不同，格雷码序列在我们从序列中的一个数字到下一个数字时只会改

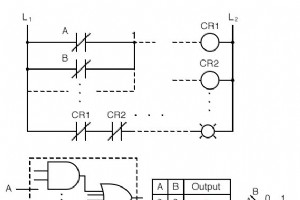
谁开发了卡诺图？ 电信工程师莫里斯·卡诺 (Maurice Karnaugh) 于 1953 年在贝尔实验室设计基于数字逻辑的电话交换电路时开发了卡诺图。 卡诺图的使用 现在我们已经借助维恩图开发了卡诺图，让我们使用它。卡诺图减少 与布尔代数相比，逻辑函数更快速、更容易。减少是指简化，减少门和输入的数量。 我们喜欢将逻辑简化为最低成本 通过消除组件来节省成本的形式。我们将最低成本定义为每个门的输入数量最少的门的数量最少。 如果有选择，大多数学生一旦学习了这个工具，就会使用卡诺图而不是布尔代数进行逻辑简化。 我们在上面展示了五个单独的项目，它们只是表示同一事物的不同方式：任

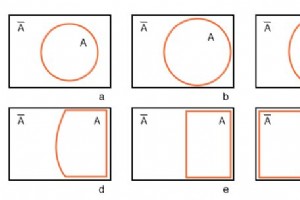
以圆 A 开头 在矩形A宇宙中 在下图 (a) 中，我们将维恩图变形为几乎是卡诺图。 我们展开圆A 在（b）和（c）处，符合矩形A’宇宙 在 (d) 处，并更改 A 到（e）处的矩形。 A 之外的任何东西 是 A .我们为 A 分配一个矩形 在（f）。此外，我们不在卡诺图中使用阴影。到目前为止，我们所拥有的类似于 1 变量卡诺图，但实用性不大。我们需要多个变量。 上图 (a) 与之前显示 A 的维恩图相同 和 A 上面除了标签 A 和 A 位于图表上方，而不是在相应区域内。想象一下，我们经历了一个类似于图 (a-f) 的过程来得到 B 的“方形维恩图” 和 B

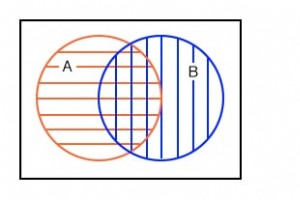
第四个例子有 A 部分重叠B .不过，我们将首先查看下面所有阴影区域的整体，然后仅查看重叠区域。让我们为上面的区域分配一些布尔表达式，如下所示。 左下方是 A 的红色水平阴影区域 . B 有一个蓝色的垂直阴影区域 . 如果我们查看两者的整个区域，无论阴影样式如何，所有阴影区域的总和，我们都会得到右上方的插图，对应于包含的 OR A, B 的函数。布尔表达式为 A+B . 这由 45o 表示 孵化区。阴影区域之外的任何内容都对应于 (A+B)-not 如上图所示。让我们继续看第四个例子的下一部分。 查看带有重叠圆圈的维恩图的另一种方式是只查看 A 共有的部分 和 B ，左下方的双阴影区

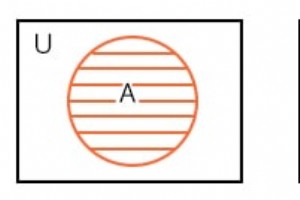
数学家使用维恩图 显示集合的逻辑关系 （对象的集合）彼此。也许您已经在代数或其他数学研究中看到过维恩图。如果你有，你可能还记得重叠的圆圈和联合 和交叉口 套。 我们将回顾维恩图的重叠圆圈。我们将采用术语 OR 和 AND 而不是并集和交集，因为这是数字电子产品中使用的术语。 维恩图将前一章的布尔代数与卡诺图联系起来。我们将把你已经知道的布尔代数与维恩图联系起来，然后过渡到卡诺图。 一套 是宇宙中对象的集合，如下所示。 成员 集合中包含的对象。集合的成员通常有一些共同点；不过，这不是必需的。 例如，在实数的宇宙中，所有正整数 {1,2,3…} 的集合是一个集合。集合 {3,4,5} 是