当冷却到超低温（接近绝对零，大约 -273 摄氏度）时，导体会失去所有电阻。必须理解，超导性不仅仅是大多数导体随温度降低而逐渐失去电阻的趋势的外推；相反，这是电阻率从有限到无的突然的飞跃。 超导材料的电阻绝对为零，而不仅仅是少量 . 超导性由荷兰莱顿大学的 H. Kamerlingh Onnes 于 1911 年首次发现。就在三年前，即 1908 年，Onnes 开发了一种液化氦气的方法，该方法提供了一种介质，可以将实验物体过冷至刚好比绝对零高几度。他决定研究当冷却到这么低的温度时汞的电阻变化，他发现它的电阻下降到没有 略低于氦的沸点。 关于超导材料究竟如何以及为什么超导存在一些争论。一种

您可能已经注意到，在特定电阻表上，所有数字都是在 20° 摄氏度的温度下指定的。如果您怀疑这意味着材料的电阻率可能会随温度变化，那么您是对的！ 特定电阻表中标准温度（通常规定为 20 摄氏度）以外的任何温度下的导体电阻值必须通过另一个公式确定： “alpha” (α) 常数被称为电阻温度系数 并表示每度温度变化的电阻变化系数。正如所有材料都具有一定的电阻率（在 20°C 时），它们也会变化 根据温度的一定数量的电阻。对于纯金属，这个系数是一个正数，意味着电阻增加 随着温度的升高。对于碳、硅和锗元素，该系数为负数，表示电阻减小 随着温度的升高。对于某些金属合金，电阻的温度系数非常接近于

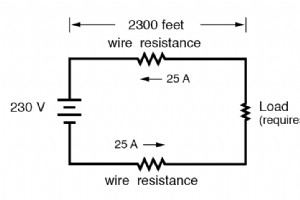
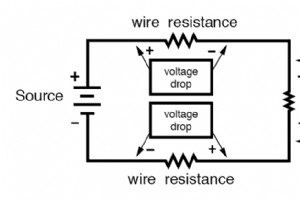
设计线阻 导体载流量额定值是基于电流产生火灾危险的可能性对电阻的粗略评估。但是，我们可能会遇到电路中导线电阻产生的电压降会引起除防火之外的其他问题的情况。例如，我们可能正在设计一个电路，其中一个组件的电压至关重要，并且不得低于某个限制。如果是这种情况，由导线电阻引起的电压降可能会导致工程问题，同时又完全在载流量的安全（火灾）限制范围内： 如果上述电路中的负载不能承受低于 220 伏的电压，假设电源电压为 230 伏，那么我们最好确保线路沿途下降不超过 10 伏。计算该电路的电源和返回导体，沿每条电线的长度留下最大可容忍的 5 伏压降。使用欧姆定律 (R=E/I)，我们可以确定每根导线的

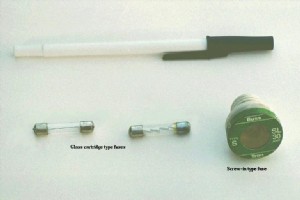
通常，导体的载流量额定值是永远不会故意超过的电路设计限制，但在某些应用中预计会超过载流量：在保险丝的情况下 . 什么是保险丝？ 保险丝 是一种围绕导电条构建的电气安全装置，该导电条设计为在电流过大时熔化和分离。保险丝总是与要防止过电流的组件串联连接，以便当保险丝熔断 （打开）它将打开整个电路并停止通过组件的电流。当然，连接在并联电路的一个支路中的熔断器不会影响通过任何其他支路的电流。 通常，保险丝的细片包含在安全护套内，以最大程度地减少电弧爆炸的危险，如果电线用猛烈的力量烧开，在严重过电流的情况下可能会发生这种情况。对于小型汽车保险丝，护套是透明的，以便可以目视检查易熔元件。过去的住宅布

任何给定电线的横截面积越小，任何给定长度的电阻越大，所有其他因素都相同。对于任何给定的电流量，电阻越大的导线将耗散更多的热能，功率等于 P=I2R。 耗散功率 由于导体的电阻以热量的形式表现出来，过热会损坏电线（更不用说电线附近的物体），特别是考虑到大多数电线都用塑料或橡胶涂层绝缘，这可以熔化并燃烧。因此，在所有其他因素相同的情况下，细线比粗线能承受的电流更小。导体的载流极限被称为它的 载流量 . 主要是出于安全原因，美国已经制定了某些电气布线标准，并在国家电气规范 (NEC) 中进行了规定 .典型的 NEC 导线载流量表将显示不同尺寸和应用的导线允许的最大电流。虽然理论上铜的熔点

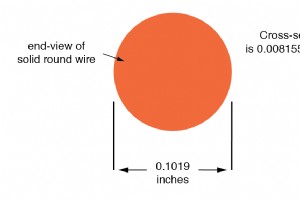
液体流过大直径管道比通过小直径管道更容易，这应该是常识（如果您想要一个实用的插图，请尝试通过不同直径的吸管喝液体）。相同的一般原理适用于通过导体的电子流动：导体的横截面积（厚度）越宽，电子流动的空间就越大，因此，流动越容易发生（电阻越小） . 电线的两种基本品种：实心和绞线 电线的横截面通常是圆形的（尽管此规则有一些独特的例外），并且有两种基本类型：实心和绞合 . 实心铜线 就像听起来一样：一根单根实心铜线，贯穿整个电线。绞合线 由较小的实心铜线绞合在一起形成单个较大的导体。绞合线最大的好处是它的机械柔韧性，能够比实心铜线更好地承受反复弯曲和扭曲（时间长了容易疲劳和断裂）。 可以通过

到现在为止，您应该很清楚导电性与某些类型材料之间的相关性。那些允许自由电子轻松通过的材料称为导体 ，而那些阻碍自由电子通过的材料被称为绝缘体 . 不幸的是，解释为什么某些材料导电而其他材料不导电的科学理论根植于电子如何围绕原子核排列的量子力学解释。与众所周知的“行星”模型相反，电子围绕原子核旋转为圆形或椭圆形轨道中定义明确的物质块，“轨道”中的电子根本不像物质。相反，它们表现出粒子和波的特征，它们的行为受到被称为“壳”和“子壳”的原子核周围不同区域内放置的限制。电子只能在有限的能量范围内占据这些区域，这取决于特定区域以及该区域被其他电子占据的程度。如果电子真的像被静电引力围绕在原子核轨道上的

当将电池连接在一起形成更大的“银行”（电池 电池？），组成电池必须相互匹配，以免引起问题。 串联电池 首先我们会考虑串联电池以获得更高的电压： 我们知道串联电路中所有点的电流都是相等的，因此任何一个串联电池中的电流量对于所有其他电池都必须相同。因此，每个电池必须具有相同的安培小时额定值，否则某些电池会比其他电池更快耗尽，从而影响整个电池组的容量。请注意，该系列电池组的总安时容量不受电池数量的影响。 电池并联 接下来，我们将考虑并联电池以获得更大的电流容量（更低的内阻）或更大的安培小时容量： 我们知道并联电路所有支路的电压相等，因此我们必须确保这些电池的电压相等。如果不是，我们将

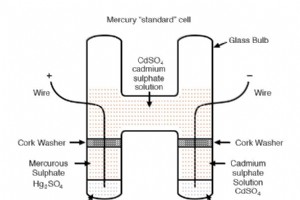
水银标准池 回到电气测量技术的早期，一种称为汞标准电池的特殊电池 被广泛用作电压校准标准。汞电池的输出为 1.0183 至 1.0194 伏直流电（取决于电池的具体设计），并且随着时间的推移极其稳定。宣传的漂移每年约为额定电压的 0.004%。汞标准电池有时被称为韦斯顿电池 或镉电池 . 不幸的是，汞电池相当不能容忍任何电流消耗，甚至无法在不影响精度的情况下使用模拟电压表进行测量。制造商通常要求通过电池的电流不超过 0.1 mA，即使这个数字也被认为是瞬间 , 或 surge 最大限度！因此，标准电池只能使用电流消耗几乎为零的电位（零平衡）设备进行测量。禁止将汞电池短路，一旦短路，该电

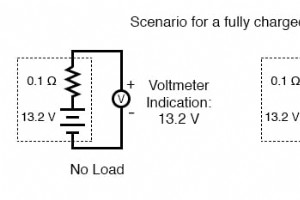
由于电池通过在离子化学反应中交换电子来在电路中产生电流，并且任何充电电池中可用于反应的分子数量有限，因此任何电池在此之前可以通过电路激发的总电荷量必须有限它的能量储备已经耗尽。电池容量可以用电子总数来衡量，但这将是一个巨大的数字。我们可以使用库仑这个单位 （等于 6.25 x 1018 电子，或 6,250,000,000,000,000,000 电子）使数量更实用，但取而代之的是一个新的单位，安培小时 ，就是为此目的而制作的。由于 1 安培实际上是每秒 1 库仑电子的流速，而一小时有 3600 秒，我们可以说库仑和安培小时之间的正比：1 安培小时 =3600 库仑。当一个旧的可以做得很好时，

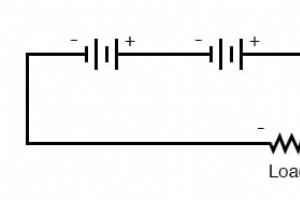
电池这个词 仅表示一组相似的组件。在军事词汇中，“电池”指的是一组枪支。在电力方面，“电池”是一组伏打电池，旨在提供比单独使用一个电池更大的电压和/或电流。 一个单元格的符号很简单，由一根长线和一根短线组成，相互平行，并带有连接线： 电池的符号只不过是几个串联的电池符号： 如前所述，任何特定类型的电池产生的电压都严格由该电池类型的化学性质决定。电池的大小与其电压无关。为了获得比单个电池输出更高的电压，必须串联多个电池。一个电池的总电压是所有电池电压的总和。典型的汽车铅酸电池有 6 个电池，标称电压输出为 6 x 2.0 或 12.0 伏： 汽车电池中的电池包含在同一个硬橡胶

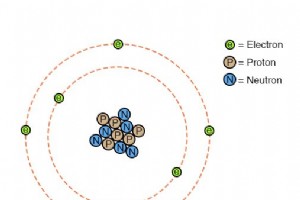
到目前为止，在我们关于电力和电路的讨论中，我们还没有详细讨论电池的工作原理。相反，我们只是假设它们通过某种神秘的过程产生恒定的电压。在这里，我们将在一定程度上探索该过程，并涵盖与实际电池及其在电力系统中的使用相关的一些实际考虑因素。 在本书的第一章中，原子的概念 讨论了，因为它是所有物质对象的基本构建块。反过来，原子由更小的物质组成，称为粒子 .电子、质子和中子是原子中发现的基本粒子类型。这些粒子类型中的每一种在原子的行为中都扮演着不同的角色。虽然电活动涉及电子的运动，但原子的化学特性（这在很大程度上决定了材料的导电性）取决于原子核（中心）中的质子数。 原子核中的质子极难移走，因此原子

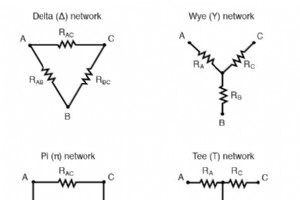
在许多电路应用中，我们会遇到以两种方式之一连接在一起形成三端网络的组件：“Delta”或 Δ（也称为“Pi”或 π）配置和“Y”（也称为“T”）配置。 可以计算形成一种网络（Δ 或 Y）所需的电阻器的正确值，该网络的行为与另一种网络相同，仅从端子连接进行分析。也就是说，如果我们有两个独立的电阻网络，一个 Δ 和一个 Y，每个电阻网络都隐藏起来，只有三个端子（A、B 和 C）暴露用于测试，电阻的大小可以根据两个网络，因此无法从电气上确定一个网络与另一个网络的区别。换句话说，等效的 Δ 和 Y 网络表现相同。 Δ 和 Y 转换方程 有几个方程用于将一个网络转换为另一个网络： Δ 和

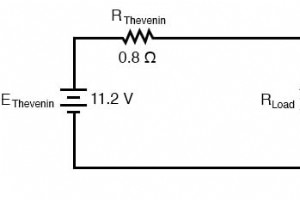
最大功率传输定理与其说是一种分析手段，不如说是对系统设计的一种辅助。简单地说，当负载电阻等于供电网络的戴维宁/诺顿电阻时，负载电阻将耗散最大功率。如果负载电阻低于或高于源网络的戴维宁/诺顿电阻，其耗散功率将小于最大值。 这基本上是无线电发射机设计的目标，其中天线或传输线“阻抗”与最终功率放大器“阻抗”匹配，以获得最大射频功率输出。阻抗是与交流和直流电流相反的整体，与电阻非常相似，并且源和负载之间的阻抗必须相等，才能将最大量的功率传输到负载。过高的负载阻抗会导致低功率输出。过低的负载阻抗不仅会导致低功率输出，而且由于其内部（戴维宁或诺顿）阻抗中耗散的功率，还可能导致放大器过热。 最大功率传输示

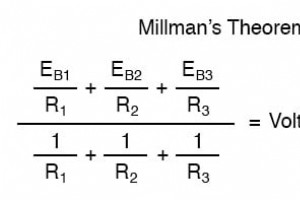
您可能想知道我们从哪里得到了用于确定电路的并联支路之间的“米尔曼电压”的奇怪公式，其中每个支路都包含一个串联电阻和电压源： 这个方程的一部分似乎与我们之前见过的方程很相似。例如，大分数的分母看起来很像我们的并联电阻方程的分母。而且，当然，大分数分子中的 E/R 项应该给出电流的数字，即欧姆定律 (I=E/R)。 既然我们已经介绍了戴维宁和诺顿源的等效性，我们就拥有了理解米尔曼方程所需的工具。 Millman 方程实际上所做的是将每个分支（及其串联电压源和电阻）视为戴维南等效电路，然后将每个分支转换为等效诺顿电路。 戴维南等效电路 因此，在上面的电路中，电池 B1 和电阻器 R1

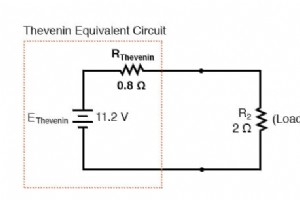
由于戴维南定理和诺顿定理是将复杂网络简化为更易于分析的两种同样有效的方法，因此必须有某种方法将戴维南等效电路转换为诺顿等效电路，反之亦然（这正是您非常想知道的， 对？）。嗯，程序很简单。 戴维宁抵抗和诺顿抵抗 您可能已经注意到，计算戴维宁电阻的过程与计算诺顿电阻的过程相同：移除所有电源并确定开路负载连接点之间的电阻。因此，同一原始网络的戴维宁和诺顿电阻必须相等。使用上两节的示例电路，我们可以看到两个电阻确实相等： 考虑到戴维宁和诺顿等效电路在向负载电阻提供电压和电流方面的行为与原始网络相同（从负载连接点的角度来看），这两个等效电路，已经推导出来自同一原始网络的行为应该相同。

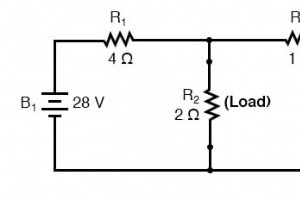
什么是诺顿定理？ 诺顿定理指出，可以将任何线性电路（无论多么复杂）简化为仅具有单个电流源和连接到负载的并联电阻的等效电路。正如戴维南定理一样，“线性”的限定与叠加定理中的限定相同：所有潜在方程都必须是线性的（没有指数或根）。 简化线性电路 将我们的原始示例电路与 Norton 等效电路进行对比：它看起来像这样： . . .诺顿转换后。 . . 请记住，当前来源 是一个组件，其工作是提供恒定量的电流，输出尽可能多或尽可能少的电压以维持该恒定电流。 戴维宁定理与诺顿定理 与戴维南定理一样，原始电路中除负载电阻外的所有内容都已简化为更易于分析的等效电路。与戴维南定理类似的还有诺顿定

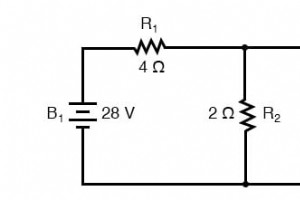
戴维南定理指出，可以将任何线性电路（无论多么复杂）简化为仅具有单个电压源和连接到负载的串联电阻的等效电路。 “线性”的限定与叠加定理中的限定相同，其中所有基本方程必须是线性的（没有指数或根）。如果我们正在处理无源元件（例如电阻器，以及后来的电感器和电容器），这是正确的。然而，有些元件（尤其是某些气体放电元件和半导体元件）是非线性的：即它们对当前变化的反对 电压和/或电流。因此，我们将包含这些类型组件的电路称为非线性电路 . 电力系统中的戴维南定理 戴维南定理在分析电力系统和其他电路时特别有用，其中电路中的一个特定电阻器（称为“负载”电阻器）会发生变化，并且需要对每个负载电阻的试验值重新计算电

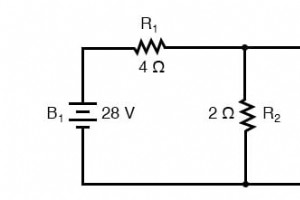
叠加定理是天才中的一种，它采用了一个复杂的主题，并以一种完全合理的方式将其简化。像米尔曼这样的定理当然很有效，但不是很明显为什么 它运作良好。另一方面，叠加很明显。 串联/并联分析 叠加定理中使用的策略是一次消除网络中除一个电源之外的所有电源，使用串联/并联分析来分别确定修改网络内每个电源的电压降（和/或电流）。然后，一旦为每个单独工作的电源确定了压降和/或电流，这些值就会全部“叠加”在彼此之上（以代数方式相加），以找出所有电源都处于活动状态时的实际压降/电流。让我们再次看一下我们的示例电路，并将叠加定理应用于它： 由于我们在这个电路中有两个电源，我们必须计算两组电压降和/或电流值，一

在米尔曼定理中，电路被重新绘制为分支的并行网络，每个分支包含一个电阻器或串联电池/电阻器组合。米尔曼定理仅适用于那些可以相应地重新绘制的电路。再次，是我们用于最后两种分析方法的示例电路： 这是相同的电路，为了应用米尔曼定理而重新绘制： 通过考虑每个分支内的电源电压和每个分支内的电阻，米尔曼定理将告诉我们所有分支上的电压。请注意，我已将最右侧分支中的电池标记为“B3”，以明确表示它位于第三个分支中，即使电路中没有“B2”！ 米尔曼定理方程 米尔曼定理只不过是一个长方程，适用于任何作为一组并联支路绘制的电路，每个支路都有自己的电压源和串联电阻： 将示例电路中的实际电压和电阻值替