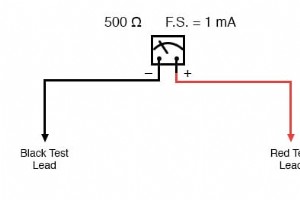
电流表测量电流 用于测量电流的仪表通常称为“电流表”，因为测量单位是“安培”。 在电流表设计中，为了扩大机芯的可用范围而添加的外部电阻器并联 与运动而不是串联，就像电压表的情况一样。这是因为我们要分流的是测得的电流，而不是测得的电压，去运动，而且分流电路总是由并联电阻组成。 设计一个电流表 以与电压表相同的仪表运动为例，我们可以看到它本身会成为一个非常有限的仪器，仅在 1 mA 时发生满量程偏转： 与扩展仪表机芯的电压测量能力的情况一样，我们必须相应地重新标记机芯的刻度，以便它在扩展的电流范围内具有不同的读数。例如，如果我们想设计一个电流表，使其满量程范围为 5 安培，使用与以前相同的

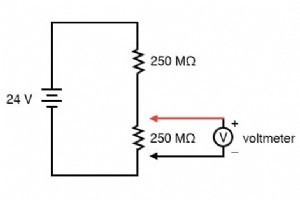
每个仪表都会在一定程度上影响它正在测量的电路，就像任何轮胎压力表都会轻微改变测量的轮胎压力，因为一些空气被释放来操作仪表。虽然有些影响是不可避免的，但可以通过良好的仪表设计将其最小化。 分压电路 由于电压表始终与被测组件并联，因此通过电压表的任何电流都会对被测电路中的总电流产生影响，从而可能影响被测电压。完美的电压表具有无限大的电阻，因此它不会从被测电路中汲取电流。然而，完美的电压表只存在于教科书的页面中，而不存在于现实生活中！以下面的分压器电路为例，说明真实的电压表如何影响其测量电路： 在没有电压表连接到电路的情况下，串联电路中的每个 250 MΩ 电阻器上应该正好有 12 伏电压，

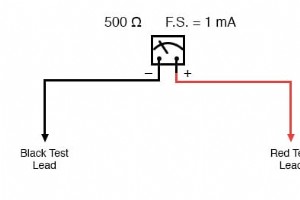
如前所述，大多数仪表运动都是敏感设备。一些 D’Arsonval 机芯的满量程偏转电流额定值低至 50 µA，（内部）线电阻小于 1000 Ω。这使得电压表的满量程额定值仅为 50 毫伏 (50 µA X 1000 Ω)！为了从这种敏感的运动中构建具有实用（更高电压）刻度的电压表，我们需要找到某种方法将测量的电压量降低到运动可以处理的水平。 DArsonval 运动计 让我们以 DArsonval 仪表机芯开始我们的示例问题，该机芯具有 1 mA 的满量程偏转额定值和 500 Ω 的线圈电阻： 使用欧姆定律 (E=IR)，我们可以确定有多少电压将驱动这个仪表直接移动到满量程： E =

一米 是为准确检测并以人类可读的形式显示电量而构建的任何设备。通常，这种“可读形式”是视觉上的：指针在刻度上的运动、排列成“条形图”的一系列灯或由数字组成的某种显示。在电路的分析和测试中，有专门用来精确测量电压、电流和电阻等基本量的仪表。还有很多其他类型的仪表，但本章主要介绍基本三种的设计和操作。 大多数现代仪表在设计上都是“数字”的，这意味着它们的可读显示是数字形式。较旧的仪表设计本质上是机械的，使用某种指针装置来显示测量量。在这两种情况下，使显示单元适用于（相对）大量电压、电流或电阻的测量所应用的原理是相同的。 什么是仪表运动？ 仪表的显示机制通常被称为运动 ，借用它的机械性来移动 沿

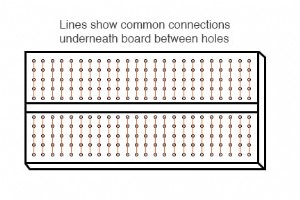
再一次，在构建电池/电阻器电路时，学生或爱好者面临着几种不同的构建模式。也许最受欢迎的是无焊面包板 ：通过将元件和电线插入互连点的网格来构建临时电路的平台。 面包板似乎只是一个塑料框架，上面有数百个小孔。但是，在每个孔下方都有一个弹簧夹，该弹簧夹连接到其他孔下方的其他弹簧夹。孔之间的连接方式简单统一： 串联 - 无焊面包板上的并联电路结构 假设我们想在面包板上构建以下串并联组合电路： 在面包板上这样做的推荐方法是以与原理图中看到的大致相同的模式排列电阻器，以便于与原理图的关系。如果需要 24 伏，而我们只有 6 伏电池可用，则可以串联四个以达到相同的效果： 这绝不是将这四个

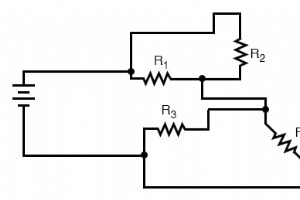
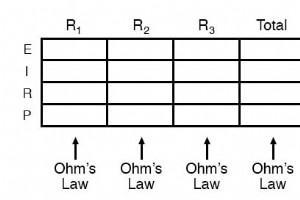
“我认为当我可以预测其解的性质，而无需实际解决它。” —P.A.M 狄拉克，物理学家 狄拉克的那句话有很多道理。稍加修改，我就可以将他的智慧扩展到电路中，说：“当我无需实际执行任何计算就可以预测对电路所做的各种更改的近似影响时，我认为我理解了电路。” 在串联和并联电路章节的最后，我们简要考虑了如何以定性分析电路 而不是定量 方式。培养此技能是成为熟练的电路故障排除者的重要一步。一旦您彻底了解任何特定故障将如何影响电路（即您不必执行任何算术来预测结果），反过来工作就会容易得多：通过评估电路的行为。 在串联和并联电路章节的末尾还展示了表格方法如何在辅助故障分析和健康电路分析方面发挥作用。

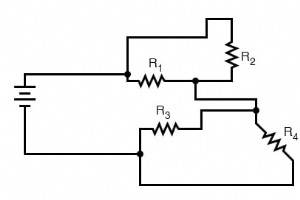
通常，复杂的电路不会排列在漂亮、整洁、干净的示意图中供我们遵循。它们通常以这样的方式绘制，以至于很难确定哪些组件是串联的，哪些是彼此并联的。本节的目的是向您展示一种有助于以整洁有序的方式重新绘制电路原理图的方法。与求解串并联组合电路的降阶策略一样，它是一种比描述更容易演示的方法。 分析和简化复杂的电路图 让我们从以下（复杂的）电路图开始。也许这张图最初是由技术人员或工程师以这种方式绘制的。也许它是在有人追踪真实电路的电线和连接时绘制的。无论如何，这里都是丑陋的： 对于电路和电路图，电路中导线连接元件的长度和布线无关紧要。 （实际上，在某些交流电路中，它变得至关重要，而且很长的导线长度会

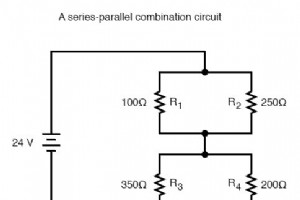
串并联组合电路分析指南 串并联电阻器电路分析的目标是能够确定电路中的所有压降、电流和功耗。实现这一目标的总体策略如下： 第 1 步： 评估电路中哪些电阻器以简单串联或简单并联的方式连接在一起。 第 2 步： 重新绘制电路，用单个等效值电阻器替换步骤 1 中确定的每个串联或并联电阻器组合。如果使用表格来管理变量，请为每个等效电阻创建一个新的表格列。 第 3 步： 重复步骤 1 和 2，直到整个电路减少到一个等效电阻。 第 4 步： 根据总电压和总电阻计算总电流 (I=E/R)。 第 5 步： 取总电压和总电流值，返回到电路简化过程的最后一步，并在适用的地方插入这些值。 第 6 步： 根据步骤

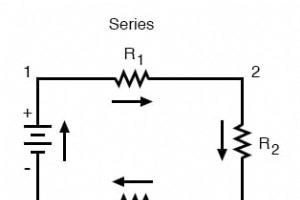
在简单的串联电路中，所有元件都首尾相连，形成只有一条电流通过电路的路径： 通过简单的并联电路，所有组件都连接在相同的两组电气公共点之间，从而为电流从电池的一端流向另一端创建多条路径： 关于串联和并联电路的规则 对于这两种基本电路配置中的每一种，我们都有描述电压、电流和电阻关系的特定规则集。 串联电路： 电压降加起来等于总电压。 所有组件共享相同（相等）的电流。 阻力相加等于总阻力。 并联电路： 所有组件共享相同（相等）的电压。 支路电流相加等于总电流。 电阻减少到等于总电阻。 串联 - 并联电路 但是，如果电路元件有些部分串联，有些部分并联，我们将无法应用单个 该

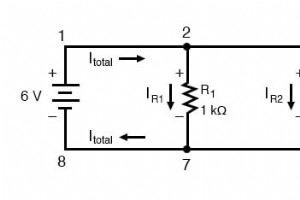
什么是基尔霍夫电流定律？ 基尔霍夫电流定律，通常缩写为 KCL，指出“所有流入和流出节点的电流的代数和必须为零。” 该定律用于描述电荷如何进入和离开导线上的接线点或节点。 有了这些信息，现在让我们看一下实践中的法律示例，为什么它很重要，以及它是如何推导出来的。 并联电路回顾 让我们仔细看看最后一个并联示例电路： 求解该电路中所有电压和电流值： 此时，我们知道电路中每个支路电流和总电流的值。我们知道并联电路中的总电流必须等于支路电流的总和，但该电路中发生的事情不止于此。看看电路中每个接线点（节点）的电流，我们应该能看到别的东西： 进入和退出节点的电流 在正“轨道”（

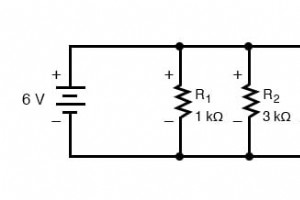
并联电路通常称为分流器 因为它能够将总电流按比例或划分为小数部分。 为了理解这意味着什么，让我们首先分析一个简单的并联电路，确定通过各个电阻的支路电流 知道并联电路中所有组件的电压相同，我们可以在电压/电流/电阻表中填入 6 伏跨过顶行： 使用欧姆定律 (I=E/R)，我们可以计算每个分支电流： 知道支路电流在并联电路中相加等于总电流，我们可以通过将 6 mA、2 mA 和 3 mA 相加得出总电流： 当然，最后一步是计算总阻力。这可以通过“总”栏中的欧姆定律 (R=E/I) 或单个电阻的并联电阻公式来完成。无论哪种方式，我们都会得到相同的答案： 再一次，考虑到

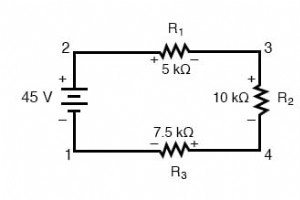
什么是基尔霍夫电压定律 (KVL)？ 被称为基尔霍夫电压定律的原理 （由德国物理学家 Gustav R. Kirchhoff 于 1847 年发现）可以这样说： “回路中所有电压的代数和必须为零” 通过代数 ，我的意思是考虑符号（极性）和大小。通过循环 ，我的意思是从回路中的一个点到该回路中的其他点，最后回到初始点的任何路径。 在串联电路中演示基尔霍夫电压定律 让我们再看看我们的示例串联电路，这次对电路中的点进行编号以供电压参考： 如果我们在点 2 和 1 之间连接一个电压表，红色测试线连接到点 2，黑色测试线连接到点 1，仪表将记录 +45 伏特。通常不显示“+”号而是隐含

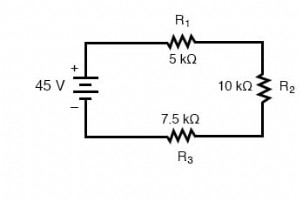
让我们分析一个简单的串联电路并确定各个电阻器上的压降： 根据各个电阻的给定值，我们可以确定总电路电阻，知道电阻串联相加： 确定总电路电阻 从这里，我们可以使用欧姆定律 (I=E/R) 来确定总电流，我们知道它与每个电阻电流相同，串联电路的所有部分的电流都相等： 使用欧姆定律计算电流 现在，知道电路电流为 2 mA，我们可以使用欧姆定律 (E=IR) 来计算每个电阻上的电压： 很明显，每个电阻器上的电压降与其电阻成正比，因为所有电阻器的电流都相同。注意 R2 两端的电压是 R1 两端电压的两倍，就像 R2 的电阻是 R1 的两倍一样。 如果我们要改变总电压，我们会发

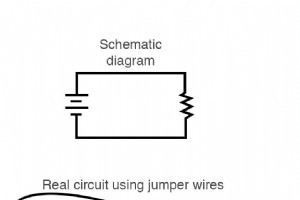
在学习电力的过程中，您将需要使用电阻器和电池构建自己的电路。在电路组装方面，有些选项可用，有些比其他选项更容易。在本节中，我将探索一些制造技术，它们不仅可以帮助您构建本章所示的电路，还可以帮助您构建更高级的电路。 使用鳄鱼夹跳线构建电路 如果我们只想构建一个简单的单电池单电阻电路，我们可以很容易地使用鳄鱼夹 像这样的跳线： 每端带有“鳄鱼”式弹簧夹的跳线提供了一种安全、方便的将组件电气连接在一起的方法。 如果我们想用一个电池和三个电阻构建一个简单的串联电路，可以应用相同的使用跳线的“点对点”构建技术： 将无焊面包板用于更复杂的电路 然而，由于跳线的笨拙及其连接的物

技术人员的工作经常需要对故障电路进行“故障排除”（定位和纠正问题）。良好的故障排除是一项艰巨而有益的工作，需要对基本概念有透彻的理解、提出假设的能力（对效应的提议解释）、根据概率判断不同假设的价值的能力（一个特定原因的可能性有多大）可能会超过另一个），以及在应用解决方案来纠正问题时的创造力。 虽然可以将这些技能提炼成一种科学的方法，但大多数有经验的故障排除人员都会同意故障排除涉及一门艺术，并且需要多年的经验才能充分发展这门艺术。 必须具备的一项基本技能是对组件故障如何影响不同配置的电路有现成且直观的理解。我们将在这里探讨串联和并联电路中元件故障的一些影响，然后在“串并联组合电路”一章的末尾

使用欧姆定律时的提示 电子学初学者在应用欧姆定律时最常犯的错误之一是混合了电压、电流和电阻的上下文。换句话说，学生可能会错误地使用通过一个电阻器的 I（电流）值和一组互连电阻器上的 E（电压）值，以为他们会得到那个电阻器的电阻。 不是这样！记住这条重要规则：欧姆定律方程中使用的变量必须通用 考虑到电路中相同的两点。我怎么强调这条规则都不为过。这在串并联组合电路中尤其重要，其中附近的组件可能具有不同的电压降和值 当前。 当使用欧姆定律计算与单个组件有关的变量时，请确保您参考的电压是穿过该单个组件的唯一电压，并且您参考的电流仅通过该单个组件，而您所参考的电阻仅为对于单个组件。同样，在计算与电

在计算电阻元件的功耗时，使用三个功率方程中的任何一个从与每个元件相关的电压、电流和/或电阻值得出答案： 这可以通过在我们熟悉的电压、电流和电阻表中添加另一行来轻松管理： 可以通过适当的欧姆定律方程（适当的 基于该列中 E、I 和 R 的数字）。 总功率与个人功率的一个有趣规则是它对任何都是可加的 电路配置：串联、并联、串联/并联或其他方式。功率是工作速率的量度，并且由于功率耗散必须 等于源施加的总功率（根据物理能量守恒定律），电路配置对数学没有影响。 评论： 力量在任何中都是可加的 电阻电路的配置： PTotal =P1 + P2 + 。 . . Pn 查看我们的收藏

当学生第一次看到并联电阻方程时，自然要问的问题是：“那个在哪里？ 东西从何而来？”这确实是一个奇怪的算术，它的起源值得好好解释一下。 电阻和电导有什么区别？ 根据定义，阻力是衡量摩擦 一个组件呈现给流过它的电流。电阻用大写字母“R”表示，单位为“欧姆”。但是，我们也可以从相反的角度考虑这种电气特性：容易 是让电流流过组件，而不是难度 . 如果阻力 是我们用来象征电流流动难易程度的词，那么一个很好的词来表达电流流动的难易程度是conductance .在数学上，电导是电阻的倒数或倒数： 电阻越大，电导越小——反之亦然。 这应该具有直观意义，因为电阻和电导是表示相同基本电气特性的相反

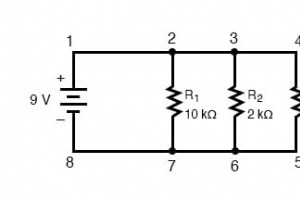
在此页面上，我们将概述您应该了解的有关并联电路的三个原则： 电压： 并联电路中所有组件的电压相等。 当前： 总电路电流等于各个支路电流的总和。 抵抗： 个人抵抗力减弱 等于较小的总电阻而不是 add 来计算总和。 让我们看一些演示这些原理的并联电路示例。 我们将从由三个电阻器和一个电池组成的并联电路开始： 并联电路中的电压 了解并联电路的第一个原则是电路中所有组件的电压相等 .这是因为并联电路中只有两组电气公共点，并且在任何给定时间测量的公共点组之间的电压必须始终相同。 因此，在上述电路中，R1两端的电压等于R2两端的电压，R2两端的电压等于R3两端的电压，即电池两端的电压。

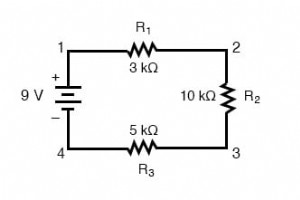
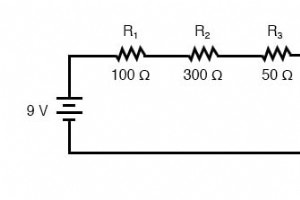
在此页面上，我们将概述您应该了解的关于串联电路的三个原则： 当前 ：通过串联电路中的任何组件的电流量都是相同的。 阻力 ：任何串联电路的总电阻等于各个电阻的总和。 电压 ：串联电路中的电源电压等于各个电压降的总和。 让我们看一些演示这些原理的串联电路示例。 我们将从由三个电阻器和一个电池组成的串联电路开始： 了解串联电路的第一个原理如下： 串联电路中通过电路中任何组件的电流量都是相同的。 这是因为在串联电路中只有一条电流路径。因为电荷像管中的弹珠一样流过导体，所以电路（管）中任意一点在任何特定时间点的流速（弹珠速度）必须相等。 在串联电路中使用欧姆定律 从 9