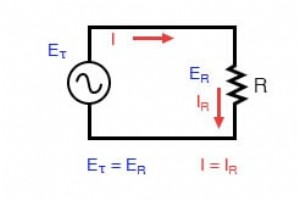
交流电路中的瞬时值 纯电阻交流电路：电阻电压和电流同相。 如果我们要绘制一个由电源和电阻组成的非常简单的交流电路的电流和电压（上图），它看起来像这样：（下图） 电阻电路的电压和电流“同相”。 由于电阻器在任何时间段都简单而直接地抵抗电流的流动，因此电阻器两端的电压降波形与通过它的电流波形完全同相。 我们可以沿图的水平轴查看任何时间点，并将这些电流和电压值相互比较（任何“快照”查看波形值都称为瞬时值 ，表示那个瞬间的值 及时）。 当电流的瞬时值为零时，电阻器两端的瞬时电压也为零。同样，在流过电阻的电流处于正峰值的时刻，电阻两端的电压也处于正峰值，依此类推。 在波

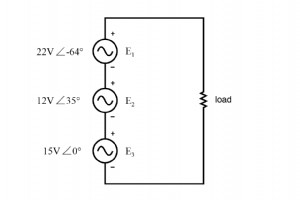
让我们将三个交流电压源串联起来，并使用复数来确定加性电压。 直流电路研究中学到的所有规则和定律也适用于交流电路（欧姆定律、基尔霍夫定律、网络分析方法），但功率计算（焦耳定律）除外。 唯一的限制是所有变量必须 以复数形式表示，同时考虑相位和幅度，并且所有电压和电流必须具有相同的频率（以便它们的相位关系保持恒定）。 （下图） KVL 允许添加复杂的电压。 所有三个电压源的极性标记都以这样一种方式定向，即它们的规定电压应相加以形成负载电阻器上的总电压。 请注意，虽然为每个交流电压源给出了幅度和相位角，但没有指定频率值。如果是这种情况，则假定所有频率都相等，从而满足我们将直流规则

复数对于交流电路分析很有用，因为它们提供了一种方便的方法来符号化表示电压和电流等交流量之间的相移。 然而，对于大多数人来说，抽象向量和实际电路量之间的等价性并不容易理解。在本章前面，我们看到了交流电压源如何以复杂的形式（幅度和 相角），以及极性标记。 由于交流电没有像直流电那样设定的“极性”，因此这些极性标记及其与相位角的关系往往令人困惑。本节旨在澄清其中一些问题。 电压本质上是相对的 数量。当我们测量电压时，我们可以选择如何将电压表或其他电压测量仪器连接到电压源，因为电压存在于两个点之间，而仪器上的两条测试线可以用来制作连接。 在直流电路中，我们明确表示电压源和电压降的极性，使用“+

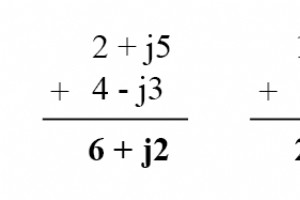
由于复数是合法的数学实体，就像标量一样，它们可以加、减、乘、除、平方、倒数等，就像任何其他类型的数字一样。 一些科学计算器被编程为直接对两个或更多复数执行这些运算，但这些运算也可以“手动”完成。本节将向您展示如何执行基本操作。 这是高度 建议您配备一个能够轻松对复数执行算术运算的科学计算器。与被迫长时间进行所有计算相比，这将使您对交流电路的研究更加愉快。 矩形复数的加减法 矩形复数的加减法很容易。对于加法，只需将复数的实部相加即可确定和的实部，将复数的虚部相加即可确定和的虚部： 以矩形形式相减复数时，只需将第一个复数的实部减去第一个复数的实部即可得到差值的实部，然后将第二个

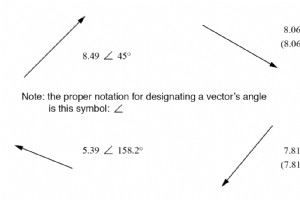
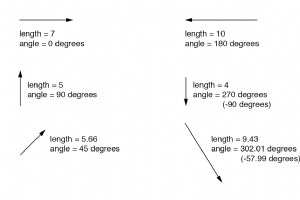
为了在不绘制向量的情况下处理复数，我们首先需要某种标准的数学符号。复数符号有两种基本形式：polar 和矩形 . 复数的极坐标形式 极坐标形式是复数由长度表示的地方 （也称为幅度 , 绝对值 , 或 模数 ) 和 角度 其向量的（通常用如下所示的角度符号表示：∠）。 使用地图类比，从纽约市到圣地亚哥的矢量的极坐标表示法类似于“西南 2400 英里”。以下是向量及其极坐标符号的两个示例： 带有极坐标符号的矢量。 交流电路计算中矢量角的标准方向将 0° 定义为向右（水平），即向上 90°、向左 180° 和向下 270°。请注意，“向下”角度的矢量的角度可以以极坐标形式表示为超

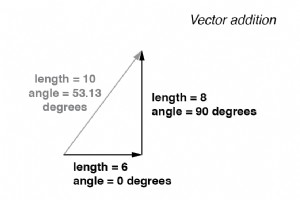
如果添加具有不常见角度的向量，它们的大小（长度）加起来与标量大小的大小非常不同：（下图） 不等角的矢量幅度不会直接相加。 如果两个异相 90° 的交流电压通过串联连接在一起，它们的电压幅值不会像直流中的标量电压那样直接相加或相减。 相反，这些电压量是复数，就像上面的向量一样，它们以三角函数的方式相加，0° 的 6 伏电源加上 90° 的 8 伏电源会产生 10 伏的相位角53.13°：（下图） 在三角函数的帮助下，6V 和 8V 电源增加到 10V。 与直流电路分析相比，这确实很奇怪。请注意，可以在两个交流电压源上分别获得 6 伏和 8 伏的电压表指示，但总电

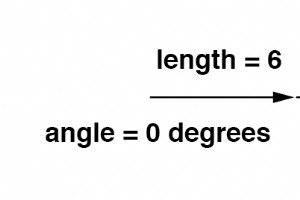
请记住，向量是数学对象，就像数轴上的数字一样：它们可以加、减、乘和除。加法可能是最容易可视化的向量运算，所以我们将从它开始。如果将具有公共角的向量相加，它们的大小（长度）相加就像常规标量一样：（下图） 同样，如果具有相同相位角的交流电压源串联在一起，它们的电压会增加，就像您对直流电池所期望的那样：（下图） 请注意两个交流电源引线旁边的 (+) 和 (-) 极性标记。尽管我们知道 AC 没有与 DC 相同意义上的“极性”，但这些标记对于了解如何参考给定的电压相角至关重要。这将在下一个示例中变得更加明显。 如果向量彼此直接相反 (180° 异相）相加，它们的幅度（长度

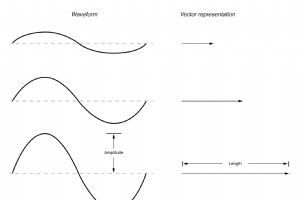
好的，那么我们如何准确地以矢量的形式表示电压或电流的交流量呢？矢量的长度代表波形的幅度（或幅度），如下所示：（下图） 波形的幅度越大，其对应向量的长度就越大。然而，矢量的角度表示所讨论的波形与另一个作​​为时间“参考”的波形之间的相移度数。 通常，在表示电路中波形的相位时，是参考电源电压波形（任意表述为“at”0°）。记住阶段总是一个相对 两个波形之间的测量，而不是绝对属性。 （下图） 两个波形之间的相移度数越大，相应矢量之间的角度差就越大。作为相对测量，作为电压，相移（矢量角）仅在参考某些标准波形时才有意义。 通常，这个“参考”波形是电路中的主要交流电

如果我需要描述两个城市之间的距离，我可以提供一个由英里、公里或其他一些线性测量单位组成的单一数字的答案。 然而，如果我要描述如何从一个城市到另一个城市旅行，我必须提供更多的信息，而不仅仅是这两个城市之间的距离；我还必须提供有关方向的信息 也去旅行。 表示线性距离等单一维度的信息类型称为标量 数学中的数量。到目前为止，标量数是您在大多数数学应用程序中使用过的那种数字。 例如，电池产生的电压是一个标量。一根导线的电阻（欧姆）或通过它的电流（安培）也是如此。 然而，当我们开始分析交流电路时，我们发现电压、电流甚至电阻（称为阻抗 在交流中）不是我们习惯于在直流电路中测量的熟悉的一维量。 相反

电最引人入胜的应用之一是产生不可见的能量涟漪，称为无线电波 .本课交流电的范围有限，无法充分探索这个概念，将涵盖一些基本原理。 随着奥斯特偶然发现电磁学，人们认识到电和磁是相互关联的。 当电流通过导体时，会产生垂直于流动轴的磁场。同样，如果导体受到垂直于导体的磁通量变化的影响，则会沿该导体的长度产生电压。 到目前为止，科学家们知道电和磁似乎总是以正确的角度相互影响。然而，在这个看似简单的相关垂直概念之下却隐藏着一项重大发现，它的揭晓是现代科学的关键时刻之一。 电场和磁场的关系 物理学上的这一突破再怎么强调也不为过。负责这场概念革命的人是苏格兰物理学家詹姆斯·克拉克·麦克斯韦 (Jame

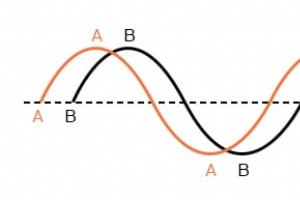
当我们需要关联两个或多个彼此不同步的交流电压或电流时，事情开始变得复杂。 “失步”是指两个波形不同步：它们的峰值和零点在同一时间点不匹配。下图中的图表说明了一个例子。 异相波形。 上面显示的两个波（A 对 B）具有相同的幅度和频率，但它们彼此不同步。在技​​术术语中，这称为相移 .早些时候我们看到了如何通过计算三角正弦函数来绘制“正弦波”，角度范围从 0 到 360 度，一个完整的圆。 正弦波的起点是零度的零幅度，90度时为全正幅度，180度时为零，270度时为全负，360度时回到零起点。 我们可以沿着波形图的水平轴使用这个角度刻度来表示一个波与另一个波的步距：下图 浪潮A

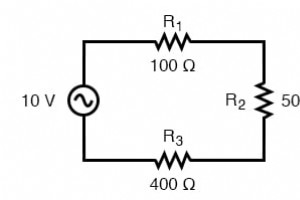
在接下来的几章中，您将了解到，由于具有电感和电容的电路中交流电的复杂性，交流电路的测量和计算会变得非常复杂。 然而，对于仅涉及交流电源和电阻的简单电路（下图），直流电的相同定律和规则简单而直接地适用。 电阻电路的交流电路计算与直流相同。 串联电阻仍然增加，并联电阻仍然减少，基尔霍夫和欧姆定律仍然适用。实际上，正如我们稍后将发现的，这些规则和法律总是 没错，只是我们必须用更高级的数学形式来表达电压、电流和电流的反量。 然而，对于纯电阻电路，交流的这些复杂性没有实际意义，因此我们可以像处理简单的直流量一样对待这些数字。 因为所有这些数学关系仍然适用，我们可以使用我们熟悉的

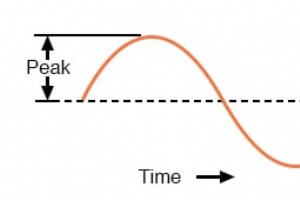
到目前为止，我们知道交流电压极性交替，交流电流方向交替。我们也知道 AC 可以以各种不同的方式交替，通过跟踪随时间的交替，我们可以将其绘制为“波形”。 我们可以通过测量波在重复之前进化所需的时间（“周期”）来测量交替率，并将其表示为每单位时间的周期或“频率”。在音乐中，频率与音高相同 ，这是区分一个音符与另一个音符的基本属性。 然而，如果我们试图表达交流量的大小，就会遇到测量问题。使用直流电，电压和电流的量通常是稳定的，我们可以毫不费力地表示电路的任何部分有多少电压或电流。 但是，您如何对不断变化的事物进行单一的量级测量？ 交流波形幅度的表示方法 表达强度或幅度（也称为幅度 )，一个交

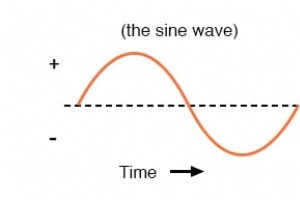
当交流发电机产生交流电压时，电压会随着时间切换极性，但会以非常特殊的方式进行。随着时间的推移，由交流发电机的这种交替极性电压所追踪的“波”呈现出独特的形状，称为正弦波 ：下图 交流电压随时间变化的图表（正弦波）。 在机电交流发电机的电压图中，从一种极性到另一种极性的变化是平滑的，电压电平在零（“交叉”）点变化最快，在其峰值变化最慢。如果我们在 0 到 360 度的水平范围内绘制“正弦”的三角函数，我们会发现与下表中的模式完全相同。 三角“正弦”函数。 角度（°） Sin（角度） 波浪 角度（°） Sin（角度） 波浪 00.0000zero1800.0000zero1

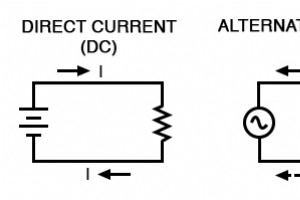
大多数电力专业的学生从所谓的直流开始他们的学习 (DC)，即电流以恒定方向流动，和/或具有恒定极性的电压。 直流电是由电池（有明确的正负极）产生的电，或者是某种材料相互摩擦产生的电荷。 交流电与直流电 与 DC 一样有用且易于理解，它并不是使用的唯一“种类”电力。某些电源（最显着的是旋转机电发电机）自然会产生极性交替的电压，随着时间的推移正负反转。 无论是作为电压切换极性还是作为电流切换方向来回，这种“类型”的电被称为交流电 (AC)： 直流电与交流电 熟悉的电池符号被用作任何直流电压源的通用符号，而带有波浪线的圆圈则是任何交流电压源的通用符号。 有人可能想知道为什么有

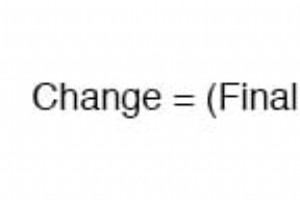
有时需要确定无功电路达到预定值所需的时间长度。在我们设计 RC 或 L/R 电路以执行精确定时功能的情况下尤其如此。为了计算这个，我们需要修改我们的“通用时间常数公式”。原来的公式是这样的： 使用通用时间常数求解时间 但是，我们要解决时间问题，而不是变化量。为此，我们对公式进行代数运算，使时间全部在等号的一侧，其余全部在另一侧： ln 时间常数项右侧的名称是自然对数 功能：与 e 的力量完全相反 .事实上，这两个函数（e 和自然对数的幂）可以这样关联： 如果 ex =a，然后ln a =x。 如果 ex =a，那么 a 的自然对数会给你 x：e 的幂 必须

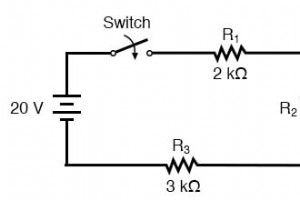
如果遇到比我们目前看到的简单串联配置更复杂的电路，我们该怎么办？以这个电路为例： 简单的时间常数公式 (τ=RC) 基于连接到电容器的简单串联电阻。就此而言，电感电路的时间常数公式 (τ=L/R) 也是基于简单串联电阻的假设。那么，在这种电阻与电容（或电感）串并联的情况下，我们该怎么办？ 戴维南定理 答案来自我们对网络分析的研究。戴维宁定理告诉我们，我们可以减少任何 通过几个简单的步骤，将线性电路转换为等效于一个电压源、一个串联电阻和一个负载组件。为了将戴维南定理应用到我们这里的场景中，我们将把电抗元件（在上面的示例电路中，电容器）视为负载，并将其暂时从电路中移除，以找到戴维南

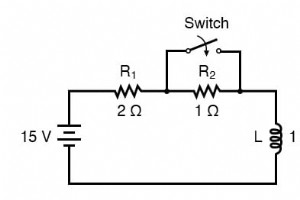
在某些情况下，当电压和电流的起始值不是完全“放电”状态时，您可能需要分析直流无功电路。换句话说，电容器可能会在部分充电状态下启动，而不是从零伏开始，而电感器可能会以一些已经通过它的电流量开始，而不是我们迄今为止假设的零电流。 以这个电路为例，从开关打开到开关在闭合位置结束： 由于这是一个电感电路，我们将通过确定电流的开始和结束值来开始我们的分析 .这一步在分析电感电路时非常重要，因为开始和结束电压 电流确定后才能知道！在开关打开（启动条件）时，总（串联）电阻为 3 Ω，将电路中的最终电流限制为 5 安培： 因此，在开关关闭之前，我们有 5 安培的电感电流通过，而不

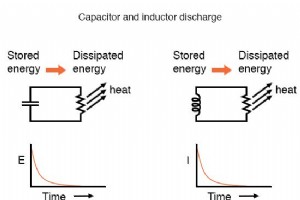
了解 L/R 时间常数 电子学的新学生常常感到困惑，为什么电感电路的时间常数计算与电容电路的时间常数计算不同。对于电阻电容电路，时间常数（以秒为单位）由以欧姆为单位的电阻与以法拉为单位的电容的乘积（乘积）计算得出：τ=RC。 然而，对于电阻-电感电路，时间常数是根据以亨利为单位的电感与以欧姆为单位的电阻的商（除法）计算得出的：τ=L/R。 这种计算上的差异对定性产生了深远的影响。 瞬态电路响应分析。阻容电路低阻反应快，高阻反应慢；电阻电感电路正好相反，高电阻响应快，低电阻慢。 虽然电容式电路对新生来说似乎没有直观的麻烦，但电感式电路的意义不大。 电容和电感能量 理解瞬态电路的关键

有一种可靠的方法可以随时间计算无功直流电路中的任何值。 计算无功直流电路中的值 第一步是确定电容器或电感器反对变化的任何数量的起始值和最终值；也就是说，无论反应成分试图保持恒定的数量。对于电容器，这个量是电压;对于电感器，这个量是电流 .当电路中的开关闭合（或打开）时，无功分量将尝试将该量保持在与开关转换之前相同的水平，因此该值将用作“起始”值。 该数量的最终值是无限时间后该数量的任何值。这可以通过分析电容电路来确定，就像电容器是开路一样，而电感电路就像电感器是短路一样，因为这是这些组件达到“完全充电”时的行为，在无限长的时间之后。 下一步是计算时间常数 电路的：在瞬态情况下，电压或电流