







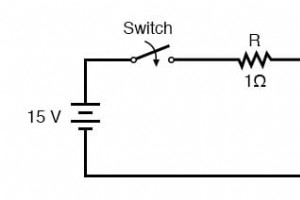
电感器具有与电容器完全相反的特性。而电容器在电中储存能量 场(由两个板之间的电压产生),电感器将能量存储在 磁性 场(由通过导线的电流产生)。因此,当电容器中存储的能量试图在其端子上保持恒定电压时,电感器中存储的能量试图保持通过其绕组的恒定电流。 正因为如此,电感器对抗电流的变化,而电容器的作用恰恰相反,后者对抗电压的变化。一个完全放电的电感器(无磁场),通过它的电流为零,当连接到电压源时(因为它试图保持零电流),最初将作为开路,从而降低其引线上的最大电压。 随着时间的推移,电感电流上升到电路允许的最大值,端电压相应下降。一旦电感器的端电压降至最低(“完美”电感器为零),电流将保持在最大水
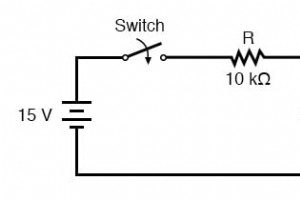
因为电容器以电场的形式储存能量,所以它们往往像小型二次电池一样,能够储存和释放电能。完全放电的电容器在其端子上保持零伏,充电后的电容器在其端子上保持稳定的电压,就像电池一样。 当电容器与其他电压源一起放置在电路中时,它们将从这些电源中吸收能量,就像二次电池连接到发电机后会充电一样。一个完全放电的电容器,其端电压为零,当连接到电压源时,最初将作为短路,在开始建立电荷时吸收最大电流。 随着时间的推移,电容器的端电压上升以满足来自电源的施加电压,并且通过电容器的电流相应地减小。一旦电容器达到电源的全电压,它将停止从中汲取电流,并且基本上表现为开路。 当开关第一次闭合时,电容器两端的

本章探讨了电容器和电感器对直流电压突然变化(称为瞬态 电压),当与电阻串联时。与电阻器对施加的电压立即做出响应不同,电容器和电感器在吸收和释放能量时会随着时间的推移做出反应。

电感器与所有电气元件一样,也有其局限性,为了可靠性和电路正常运行,必须遵守这些局限性。 影响电感的因素 额定电流 由于电感器是由线圈构成的,任何导线的载流能力都会受到电阻和散热能力的限制,因此必须注意允许通过电感器的最大电流。 等效电路 由于电感线具有一定的电阻,并且电路设计约束通常要求将电感构建为尽可能小的尺寸,因此没有“完美”电感这样的东西。电感线圈导线通常具有大量的串联电阻,并且线圈匝与另一匝线圈之间的距离很近(由绝缘体隔开)可能会产生可测量的杂散电容,从而与其纯电感特性相互作用。 与相对容易制造且杂散效应可忽略不计的电容器不同,电感器很难找到“纯”形式的。在某些应用中,这些不
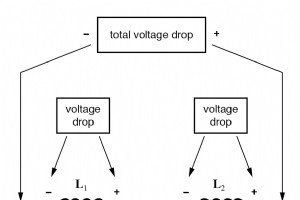
当电感串联时,总电感是各个电感的电感之和。要理解为什么会这样,请考虑以下因素:电感的最终衡量标准是在给定的电流变化率下,电感两端的电压下降量。 如果电感串联在一起(因此共享相同的电流,并看到相同的电流变化率),那么由于电流变化而导致的总电压下降将与每个电感相加,从而产生更大的总电压比任何一个单独的电感器都好。对于相同的电流变化率,更大的电压意味着更大的电感。 因此,串联电感的总电感大于任何一个单个电感的电感。计算串联总电感的公式与计算串联电阻的公式相同: 当电感并联时,总电感小于任何一个并联电感的电感。同样,请记住,电感的最终衡量标准是在给定的电流变化率下,电感两
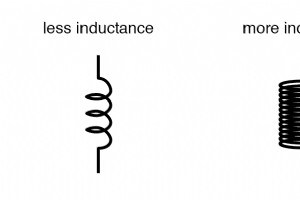
电感器结构的四个基本因素决定了产生的电感量。这些因素都通过影响给定的磁场力(通过电感线圈的电流)产生的磁场通量来决定电感: 绕线数或线圈中的“匝数” 在所有其他因素相同的情况下,线圈中的导线匝数越多,电感越大;线圈中的导线匝数越少,电感就越小。 解释: 对于给定的线圈电流量,更多匝数意味着线圈将产生更大的磁场力(以安培匝数为单位!)。 线圈面积 在所有其他因素相同的情况下,更大的线圈面积(通过线圈纵向观察,在铁芯的横截面处测量)导致更大的电感;较小的线圈面积导致较小的电感。 解释: 对于给定的场力(安培匝数),较大的线圈面积对磁场通量形成的阻力较小。 线圈长度

电感器不像导体那样具有稳定的“电阻”。但是,电感的电压和电流之间存在明确的数学关系,如下所示: 您应该从电容器章节中认识到这个方程的形式。它将一个变量(在本例中为电感电压降)与变化率相关联 另一个变量(在这种情况下,电感电流)。电压 (v) 和电流变化率 (di/dt) 都是瞬时 :也就是说,相对于特定的时间点,因此是小写字母“v”和“i”。 与电容器公式一样,习惯上将瞬时电压表示为 v 而不是e ,但使用后一个名称不会错。电流变化率(di/dt)以每秒安培为单位表示,正数代表增加,负数代表减少。 与电容器一样,电感器的行为植根于时间变量。除了电感线圈固有的任何电阻(在本节中,我
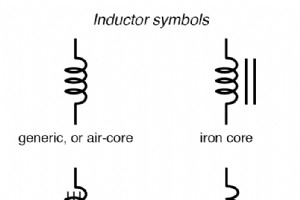
每当电子流过导体时,该导体周围就会产生磁场。这种效应称为电磁 . 磁场会影响原子中电子的排列,并且会导致原子之间穿过空间产生物理力,就像电场在带电粒子之间产生力一样。与电场一样,磁场可以占据完全空白的空间,并在远处影响物质。 场力和场通量 字段有两个度量:一个字段 force 和一个字段 flux .场力 是场在一定距离内施加的“推动”量。场flux 是通过空间的场的总量或效应。场力和通量分别大致类似于通过导体的电压(“推动”)和电流(流动),尽管场通量可以存在于完全空的空间中(没有电子等粒子的运动),而电流只能发生那里有自由电子可以移动。 场通量可以在空间中对抗,就像电子流可以被电阻对

如果两个线圈相互靠得很近,使一个线圈的磁场与另一个线圈相连,那么第二个线圈中就会产生电压。这称为互感 :当施加在一个线圈上的电压在另一个线圈上感应出电压时。 专门设计用于在两个或多个线圈之间产生互感效应的装置称为变压器 . 上图所示的装置是一种变压器,带有两个同心线圈。它实际上是作为互感的精密标准单位,但为了说明变压器的本质是什么就足够了。 可以通过颜色区分两个线圈:管子的大部分长度包裹在绿色绝缘线(第一个线圈)中,而第二个线圈(带有青铜色绝缘体的电线)位于管子的中间长度。电线末端向下延伸至设备底部的连接端子。大多数变压器装置的线圈不是这样暴露的。 因为只有当磁场通量发生变
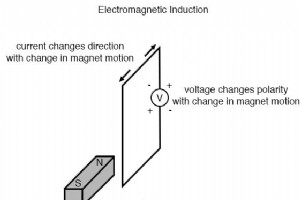
虽然奥斯特惊人的电磁学发现为更实际的应用铺平了道路 在电力方面,迈克尔法拉第给了我们实用发电的钥匙 电:电磁感应 .法拉第发现,如果电线暴露在强度变化的垂直磁场通量中,则会在电线上产生电压。 创建强度变化的磁场的一种简单方法是将永磁体移动到电线或线圈旁边。 记住: 垂直于导线的磁场强度必须增加或减少(以便磁通线“穿过” 指挥 ),否则不会感应出电压。 法拉第能够在数学上将磁场通量的变化率与感应电压相关联(注意电压使用小写字母“e”。这是指瞬时 电压,或特定时间点的电压,而不是稳定、稳定的电压。): “d”项是标准的微积分符号,表示通量随时间的变化率。 “N”代表线圈中的匝数或
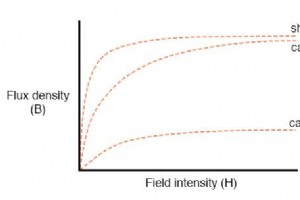
可以绘制材料渗透率的非线性以更好地理解。我们将场强 (H) 的数量,等于场力 (mmf) 除以材料的长度,放在图表的水平轴上。在纵轴上,我们将放置通量密度 (B) 的数量,它等于总通量除以材料的横截面积。 我们将使用场强 (H) 和通量密度 (B) 的量而不是场力 (mmf) 和总通量 (Φ),以便我们的图形形状保持独立于我们测试材料的物理尺寸。我们在这里试图做的是展示任何场力和通量之间的数学关系 一块特定物质,与描述材料的特定电阻具有相同的精神 以 ohm-cmil/ft 而不是它的实际电阻 以欧姆为单位。 这称为正常磁化曲线 , 或 B-H 曲线 , 对于任何特定材料。请注
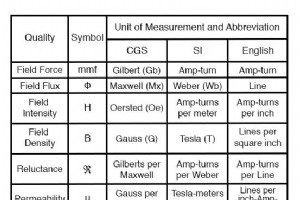
如果常见数量的两种测量系统(英制与公制)的负担让您感到困惑,那么这里不适合您!由于早期磁学缺乏标准化,我们一直受到不少于三个完整的磁量测量系统的困扰。 首先,我们需要熟悉与磁性相关的各种量。与电气系统相比,磁系统要处理的量要多得多。对于电,基本量是电压 (E)、电流 (I)、电阻 (R) 和功率 (P)。 前三个通过欧姆定律相互关联(E=IR ;I=E/R ;R=E/I),而功率通过焦耳定律与电压、电流和电阻相关(P=IE ;P=I2R; P=E2/R). 有了磁力,我们需要处理以下数量: 磁动势 ——磁场力或“推力”的量。类似于电压(电动势)。 场通量 ——总场效应的数量,或场
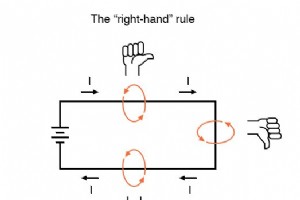
与许多其他科学发现一样,磁与电之间关系的发现几乎是偶然发现的。 1820 年的一天,丹麦物理学家汉斯·克里斯蒂安·奥斯特 (Hans Christian Oersted) 正在讲授可能性 电和磁是相互关联的,并在此过程中在全班同学面前通过实验最终证明了这一点! 通过让电流通过悬挂在磁罗盘上方的金属线,奥斯特能够根据电流使罗盘指针产生一定的运动。课堂开始时的猜测在最后被证实为事实。不用说,奥斯特必须为以后的课程修改他的讲义!他的偶然发现为一个全新的科学分支铺平了道路:电磁学。 详细的实验表明,电流产生的磁场总是垂直于流动方向。显示这种关系的一种简单方法称为右手法则 .简单地说,右手定则说
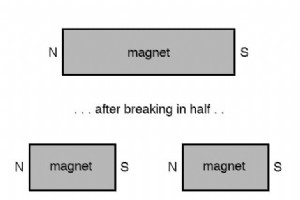
几个世纪前,人们发现某些类型的矿物岩石对金属铁具有不同寻常的吸引力。一种特殊的矿物,称为磁石 , 或 磁铁矿 , 在非常古老的历史记录中被发现(大约 2500 年前在欧洲,远东更早)作为一个好奇的主题。 后来,它被用于导航,因为发现如果让这种不寻常的岩石自由旋转(悬挂在绳子上或漂浮在水中),它的一块将倾向于南北方向. Peter Peregrinus 于 1269 年进行的一项科学研究表明,在与一块磁石的一个“磁极”摩擦后,钢可以类似地“带电”这种不寻常的特性。 与电荷不同(例如当琥珀与布摩擦时观察到的电荷),磁性物体具有两个相反作用的极,在它们自我定向到地球后分别表示为“北”和“南”。
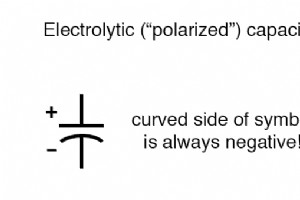
与所有电子元件一样,电容器也有一些限制,为了可靠性和正确的电路操作,必须考虑这些限制。 电容器工作电压 工作电压 :由于电容器只不过是由绝缘体(电介质)隔开的两个导体,因此您必须注意其上允许的最大电压。如果施加过大的电压,可能会超过介电材料的“击穿”额定值,导致电容器内部短路。 电容器极性 极性 :某些电容器在制造时只能承受一种极性的施加电压,而不能承受另一种极性。这是由于它们的结构:电介质是在制造过程中通过直流电压沉积在其中一个板上的微观绝缘层。这些被称为电解 电容器 , 并清楚地标明了它们的极性。 反转电解电容器的电压极性可能会导致超薄介电层的破坏,从而损坏设备。然而,该电介质
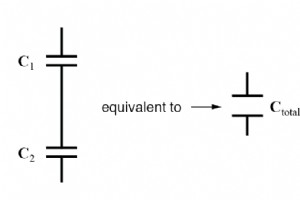
当电容器串联时,总电容小于任何一个串联电容器的单个电容。如果两个或多个电容器串联连接,则整体效果是单个(等效)电容器具有单个电容器的极板间距总和的效果。正如我们刚刚看到的,在所有其他因素不变的情况下,增加极板间距会导致电容降低。 因此,总电容小于任何单个电容器的电容。串联总电容的计算公式与并联电阻的计算公式相同: 当电容器并联时,总电容是单个电容器的电容之和。如果两个或多个电容器并联连接,则整体效果是单个等效电容器具有单个电容器的极板面积总和的效果。正如我们刚刚看到的,在所有其他因素不变的情况下,增加极板面积会导致电容增加。 因此,总电容大于任何单个电容器的电容。并联总电容的
电容器结构的三个基本因素决定了产生的电容量。这些因素都通过影响给定的电场力(两个板之间的电压)产生多少电场通量(板之间电子的相对差异)来决定电容: 盘区 :所有其他因素相同,板面积越大,电容越大;极板面积越小,电容越小。 解释: 对于给定的场力(跨板上的电压),较大的板面积会导致更多的场通量(板上收集的电荷)。 板间距 :所有其他因素相同,板间距越大,电容越小;极板间距越小,电容越大。 解释: 更近的间距会导致更大的场力(电容器两端的电压除以板之间的距离),这会导致对施加在板上的任何给定电压的更大场通量(板上收集的电荷)。 介电材料 :所有其他因素相同,介电常数越大,电容越大
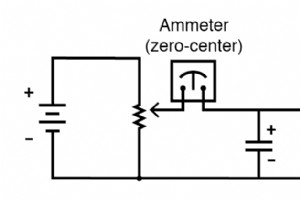
电容器不像导体那样具有稳定的“电阻”。但是,电容器的电压和电流之间存在明确的数学关系,如下所示: 小写字母“i”象征瞬时 电流,表示特定时间点的电流量。这与未指定时间段内的恒定电流或平均电流(大写字母“I”)形成对比。 “dv/dt”这个表达是从微积分中借来的,意思是电压随时间的瞬时变化率,或电压在特定时间点的变化率(伏特每秒增加或减少),同一特定点在参考瞬时电流的时间。无论出于何种原因,字母 v 通常用来表示瞬时电压而不是字母e .但是,将瞬时电压变化率表示为“de/dt”并没有错。 在这个等式中,我们看到了迄今为止我们在电路方面的经验中的一些新事物:时间变量 .当将电压、电流和
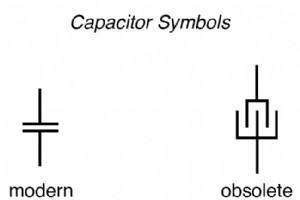
简介 每当两个分离的导体之间存在电压时,这些导体之间的空间内就会存在电场。在基本电子学中,我们研究电压、电流和电阻的相互作用,因为它们与电路有关,电路是电子可以通过的导电路径。然而,当我们谈论领域时,我们正在处理可以散布在空白空间中的交互。 诚然,“场”的概念有些抽象。至少在电流的情况下,想象称为电子的微小粒子在导体内的原子核之间移动并不困难,但“场”甚至没有质量,根本不需要存在于物质中. 尽管它是抽象的,但几乎我们每个人都对场有直接的经验,至少是以磁铁的形式。你有没有玩过一对磁铁,注意到它们如何根据它们的相对方向相互吸引或排斥?一对磁铁之间存在着不可否认的力,而这种力是没有“实质”的。

绝缘材料中的原子具有非常紧密结合的电子,可以很好地抵抗自由电子流动。然而,绝缘体不能抵抗无限量的电压。施加足够的电压后,任何 绝缘材料最终会屈服于电气“压力”,然后就会产生电流。然而,与电流与施加电压成线性比例(给定电阻)的情况不同,通过绝缘体的电流是非常非线性的:对于低于某个阈值的电压,实际上没有电流流动,但如果施加的电压超过该阈值电压(称为击穿电压 或介电强度 ),会有一股电流。 介电强度 是引起电介质击穿所需的电压 ,即强制电流通过绝缘材料。在介电击穿之后,材料可能会或可能不会再表现为绝缘体,分子结构已因破裂而改变。击穿时电流流过的绝缘介质通常存在局部“击穿”。 绝缘材料的厚度
工业技术